| Autor |
Nachricht |
munich
Anmeldungsdatum: 04.02.2006
Beiträge: 255
|
 munich Verfasst am: 13. Nov 2007 16:05 Titel: Elektrisches Potenzial einer Kugel munich Verfasst am: 13. Nov 2007 16:05 Titel: Elektrisches Potenzial einer Kugel |
 |
|
Hey Leute,
ich hab folgendes Problem.
Ich soll das Potenzial einer homogen geladener Kugel explizit berechnen.
Heißt gegeben hab ich das Integral  und das soll ich jetzt explizit für die homogen geladene kugel berechnen, innerhalb und außerhalb der Kugel. Gut, Integral in Kugelkoordinaten is ja prinzipiell kein Problm, ich weiß nur nicht, wie ich das und das soll ich jetzt explizit für die homogen geladene kugel berechnen, innerhalb und außerhalb der Kugel. Gut, Integral in Kugelkoordinaten is ja prinzipiell kein Problm, ich weiß nur nicht, wie ich das  ausdrücken soll. ausdrücken soll.
Gut, ich drück dann hald r und r' in Kugelkoordinaten aus und zieh sie von einander ab, aber dann bekomm ich im Nenner nen Ausdruck unter der Wurzel, wegen dem Betrag des Vektors und wie ich den integrieren kann, hab ich keine Idee...
Vielleicht könnt ihr mir helfen, wie drück ich den Abstand des Ortsvektors r von dem Volumenelement aus, das ich betrachte?
thx,
munich |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 13. Nov 2007 18:49 Titel: isi1 Verfasst am: 13. Nov 2007 18:49 Titel: |
 |
|
Geht es nicht ohne Integrieren, munich?
Alte Kapazitätsdefinition einer Kugel: (1) 
(2) 
mit Potential gegen unendlich U in V/m
eingesetzt
(3) an der Kugeloberfläche: 
außerhalb nimmt das Potential mit 1/r ab: 
innerhalb nimmt die Feldstärke linear auf 0 ab - dumm, jetzt muss ich doch integrieren von r_0 bis zur Kugelmitte, wobei das Startpotential das mit (3) errechnete Potential ist.
(4) innerhalb:  )
Bitte genau nachrechnen. :)
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
munich
Anmeldungsdatum: 04.02.2006
Beiträge: 255
|
 munich Verfasst am: 13. Nov 2007 19:33 Titel: munich Verfasst am: 13. Nov 2007 19:33 Titel: |
 |
|
Ja, das kann schon sein, aber die Aufgabe verlangt hald, dass wir das Potenzial explizit berechnen, zur Übung eben...
Habt ihr denn da ne Idee?
thx,
munich |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 13. Nov 2007 19:59 Titel: as_string Verfasst am: 13. Nov 2007 19:59 Titel: |
 |
|
Hallo!
Ich würde ja den Aufpunkt r erstmal auf einen Punkt auf der z-Achse beschränken. Dann hast Du nämlich den Winkel 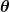 zwischen r' und z-Achse. Dann kannst Du den Abstand zwischen r' und r ausrechnen (ich denke, mit Kosinus-Satz) und dann über |r'| und Theta integrieren (bzw. ist da meistens eine Substitution mit cos(Theta) sehr hilfreich, wenn ich mich recht erinnere...). Die zwischen r' und z-Achse. Dann kannst Du den Abstand zwischen r' und r ausrechnen (ich denke, mit Kosinus-Satz) und dann über |r'| und Theta integrieren (bzw. ist da meistens eine Substitution mit cos(Theta) sehr hilfreich, wenn ich mich recht erinnere...). Die  -Integration ist ja dann einfach, weil der Abstand dort konstant bleibt. Da bekommst Du also immer nur einen Faktor -Integration ist ja dann einfach, weil der Abstand dort konstant bleibt. Da bekommst Du also immer nur einen Faktor 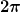 raus. raus.
Ich weiß nicht, ob das für die Aufgabe genügt. Da das Problem kugelsymmetrisch ist, kannst Du eigentlich ja die z-Achse immer in Richtung r "drehen". Normalerweise sollte das genügen dann... Für ein allgemeines r fällt mir da auch kein Trick ein.
Übrigens solltest Du über r' integrieren. Du rechnest ja ) aus und r' ist ein Vektor, der auf ein Volumenelement in der Ladungsverteilung zeigt. aus und r' ist ein Vektor, der auf ein Volumenelement in der Ladungsverteilung zeigt.
Gruß
Marco |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 14. Nov 2007 11:42 Titel: isi1 Verfasst am: 14. Nov 2007 11:42 Titel: |
 |
|
| munich hat Folgendes geschrieben: | | Ja, das kann schon sein, aber die Aufgabe verlangt halt, dass wir das Potenzial explizit berechnen, zur Übung eben... |
Wo siehst Du da das Problem, Munich?
Ich fürchte, Du hast meinen Beitrag nicht wirklich gelesen, es steht eigentlich - wenn auch nicht genau ausgeführt - schon alles Wesentliche da, oder? Wir wollen ja auch dem Fragesteller noch etwas kreative Arbeit übrig lassen, damit er was lernt und auch ein Erfolgserlebnis hat.
Aber wenns zu knapp war, hier nochmal zum Mitschreiben ;)
1. E in V/m ist auf der von Marco vorgeschlagenen z-Achse leicht zu bestimmen.
2. Dieses E dann auf der z-Achse integriert ergibt das Potential, oder?
zu 1:
An der Oberfläche ) einer Kugel ist einer Kugel ist 
Die Oberfläche  = 4\pi \cdot r^2)
Die Ladung bis r0 ist  = \rho * V(r) = \rho * \frac{4\pi}{3} r^3) ....Über r0 bleibt der Wert für r0 ....Über r0 bleibt der Wert für r0
Damit ist die el. Feldstärke E einfach durch Einsetzen hinzuschreiben:
von r=0 bis r0:  = \frac{\rho * \frac{4\pi}{3} r^3}{4\pi\epsilon \cdot r^2} = \frac{\rho * r}{3\epsilon}) darüber darüber  = \frac{\rho * r_0^3}{3\epsilon} \cdot \frac{1}{r^2})
zu 2. Da das Potential im Unendlichen Null sein soll, beginnen wir dort mit dem Integrieren:
 = \int_{\infty }^{r} -E(z)dz = \frac{-\rho * r_0^3}{3\epsilon}\ \cdot \ \int_{\infty }^{r} \frac{dz}{z^2} \ = \ \frac{\rho * r_0^3}{3\epsilon}\ \cdot \ \frac{1}{r} )
ab r0 nach innen muss man die andere Formel für E(r) weiter integrieren:
 = \frac{\rho * r_0^2}{3\epsilon} \ +\ \int_{r_0 }^{r} E(z)dz )
= \frac{\rho \cdot r_0^2}{3\epsilon}\ + \ \frac{\rho}{3\epsilon}\ \cdot \ \int_{r_0 }^{r} z dz \ =\ \frac{\rho * r_0^2}{3\epsilon}\ - \ \frac{\rho}{3\epsilon}\cdot \left( \frac{r_0^2-r^2}{2}\right))
= \frac{\rho \cdot r_0^2}{2\epsilon} \cdot \left( 1-\frac{r^2}{3 r_0^2} \right) )
Wenn noch Fragen offen sind, bitte gerne weiter fragen, Munich.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 14. Nov 2007 14:05 Titel: schnudl Verfasst am: 14. Nov 2007 14:05 Titel: |
 |
|
Du hast schon recht @isi, aber es soll eben explizit gezeigt werden, mittels Green'scher Funktion und der gegebenen Ladungsverteilung (obwohl man da nach einem allgemeinen Ansatz wieder den "Notausgang" nehmen könnte). Da das Problem radialsymmetrisch ist, wäre es natürlich viel eleganter, es so zu machen wie du vorschlägst. Aber oft bringt es auch aus didaktischen (?) Gründen etwas, die Maschinerie mal komplett durchzuziehen um dann zu sehen, dass das richtige rauskommt.
So sehs ich. 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 14. Nov 2007 15:50 Titel: isi1 Verfasst am: 14. Nov 2007 15:50 Titel: |
 |
|
Ah, ich verstehe, Schnudl,
wenn man Munichs Aufgabenstellung liest, sieht man klar, er will die Mathematik, nicht die Elektrotechnik. Übrigens habe ich den Gauß-Satz verwendet (O * D = V * ρ), von dem die Green-Sätze abgeleitet sind.
Für mich war jedenfalls überraschend, dass das Potential im Inneren der Kugel nur noch so wenig ansteigt.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
twb8t5
Anmeldungsdatum: 10.08.2011
Beiträge: 70
|
 twb8t5 Verfasst am: 26. Jan 2013 19:13 Titel: twb8t5 Verfasst am: 26. Jan 2013 19:13 Titel: |
 |
|
Vergleichbare Threads sind:
http://www.physikerboard.de/lhtopic,26174,0,0,asc,.html <= ! (26. Jan 2013 15:53)
http://www.physikerboard.de/lhtopic,31619,0,0,asc,.html
http://www.physikerboard.de/lhtopic,22524,0,0,asc,.html
Das Problem ist nicht mit dem Integral zu lösen, da die Entfernung zur Ladung im Integralbereich zu Null wird und somit eine Singularität erzeugt.
Es gibt jedoch eine Alternative. Wir trennen die Kugel in zwei Teile: Eine innere Kugel und den Rest als Kugelschale der Dicke R-r.
Das Potential auf der Oberfläche der Teilvollkugel ist einfach.
Wir wissen, dass das Potential im Inneren einer Hohlkugel konstant ist. Wir brauchen nun nur noch das Potential auf der Innenseite der Hohlkugel.
Nun brauchst Du also nur das Potenzial\Potential der Hohlkugel im Ursprung berechnen.
Eine weitere Möglichkeit ist es die Poisson-Gleichung zu lösen. Diese Vorgehensweise ist hier:
http://hp.physnet.uni-hamburg.de/pfannkuche/E-Dynamik_04/vorlesungen/vorlesung4.pdf
ab Seite 5 Kapitel 3.2.2 dargestellt.
Die Lösung von isi1 am 13. Nov 2007 stimmt übrigens auch. |
|
 |
|
|
















