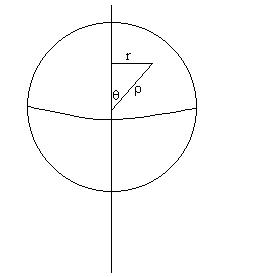
| Trägheitsmoment einer Kugel |
| Autor | Nachricht | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Passepartout Anmeldungsdatum: 02.06.2005 Beiträge: 172 Wohnort: Lausanne |
|
|||||||||||||||||
| Passepartout Anmeldungsdatum: 02.06.2005 Beiträge: 172 Wohnort: Lausanne |
|
|||||||||||||||||
| Bimmel Anmeldungsdatum: 11.07.2005 Beiträge: 5 |
|
|||||||||||||||||
| Gast |
|
|||||||||||||||||
| Gast |
|
|||||||||||||||||
| Passepartout Anmeldungsdatum: 02.06.2005 Beiträge: 172 Wohnort: Lausanne |
|
|||||||||||||||||
| sax Anmeldungsdatum: 10.05.2005 Beiträge: 377 Wohnort: Magdeburg |
|
|||||||||||||||||
| MAPster Anmeldungsdatum: 16.09.2013 Beiträge: 1 |
|
|||||||||||||||||
| Namenloser324 Gast |
||||||||||||||||||
| Verwandte Themen - die Neuesten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Trägheitsmoment eines homogenen Vollzylinders | 2 | Gast | 4868 | 11. Jan 2024 11:19 Mathefix |
 |
Trägheitsmoment eines Sterns | 21 | izzy | 5435 | 16. Dez 2023 22:22 TomS |
 |
Vollzylinder und Kugel: was kommt höher? | 3 | Gast | 1031 | 28. Nov 2023 18:57 Qubit |
 |
Kugel an Seil vmax berechnen | 8 | Gast | 4220 | 30. Nov 2023 11:03 Mathefix |
 |
Ladung Kugel | 1 | laser1960 | 3140 | 12. Nov 2023 11:12 Myon |
| Verwandte Themen - die Größten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Kugel auf Tisch | 57 | Rebecka 2 | 7692 | 27. Mai 2021 13:15 Ich |
 |
Welche Kugel kommt schneller unten an? | 47 | Veryyy | 13906 | 01. Okt 2021 12:16 TomS |
 |
Trägheitsmoment | 47 | NikolasGauß | 14795 | 19. Dez 2013 02:42 GvC |
 |
Die Kugel ist rund und soll es auch bleiben | 44 | Azkaenion | 6931 | 26. Mai 2021 15:08 Mathefix |
 |
Schwerpunkt und Trägheitsmoment | 40 | mariechen | 20595 | 02. Dez 2010 19:52 the_wire |
| Verwandte Themen - die Beliebtesten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Trägheitsmoment Quader Integral | 30 | Das Original | 57945 | 12. Dez 2007 16:58 Gimel |
 |
Trägheitsmoment einer Scheibe | 4 | Fitz Oplong | 45373 | 26. Okt 2014 14:25 franz |
 |
Trägheitsmoment einer dünnen Hohlkugel | 4 | bReet | 40241 | 14. Feb 2005 20:36 etzwane |
 |
geladene Kugel im E-Feld: Auslenkung/Bewegung | 32 | Kotelett | 36846 | 07. Jun 2006 00:05 as_string |
 |
Trägheitsmoment Kegel | 11 | Orpheus | 35836 | 12. Jul 2012 19:00 Loxeran |

 )
)
 ,
,