| Autor |
Nachricht |
NikolasGauß
Gast
|
 NikolasGauß Verfasst am: 17. Dez 2013 19:52 Titel: Trägheitsmoment NikolasGauß Verfasst am: 17. Dez 2013 19:52 Titel: Trägheitsmoment |
 |
|
Tach, ich setze michd erzeit mit dem sogenannten Trägheitsmoment auseinander, wobei ich gerne folgende Aufgabe lösen möchte
Die Dichte �eines Kreiszylinders (Radius R = 10 cm, Höhe H = 20 cm) nehme gemäß p=p0(1+(r/R)^2) mit dem Abstand von der Figurenachse zu.
Wie groß ist sein Trägheitsmoment bei Rotation um die Figurenachse, wenn p�0 =2000 kg/m3 ist. (Geben Sie das Ergebnis in Abhängigkeit von der Masse an.)
Meine Frage:
Ich muss nun mithilfe dem Volumina Integral (Dreifachintegral) p*R^2 das Rrägheitsmoment bzgl. dieser vorgegeben Dichte herleiten, wobei r außerdem nur eine konstante ist. Integral lösen und fertig ist die Aufgabe ? |
|
 |
Wiktoria
Gast
|
 Wiktoria Verfasst am: 17. Dez 2013 21:13 Titel: Wiktoria Verfasst am: 17. Dez 2013 21:13 Titel: |
 |
|
r ist keine Konstante.
Du brauchst dazu auch kein dreifaches Integral.
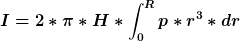
ergibt I=1,03*H |
|
 |
NikolasGauß
Gast
|
 NikolasGauß Verfasst am: 17. Dez 2013 21:36 Titel: NikolasGauß Verfasst am: 17. Dez 2013 21:36 Titel: |
 |
|
Klasse, hätte nicht gedacht das jemand so schnell antworten wird. xD
Du hast genau geantwortet indem Moment wo ich etwas schreiben wollte.Da die Aufgabe mit Massenabhängigkeit zu lösen ist (Ist das bei deiner Rechnung berücksichtigt wurden?) könnte ich da wie folgt vorgehen (Ignoriere bitte meinen ersten Post xD):
Für die Dichte gilt p=m/V=m/(2000*pi). Daraus folgt:
Volumina Integral R^2 *p(R)dV=Volumina Integral 100*m/V dV=Volumina Integral 100*m/(2000/pi)dV.
Aber dann verschwindet das r, weisst du welchen Denkfehler ich hier mach? |
|
 |
NikolasGauß
Gast
|
 NikolasGauß Verfasst am: 17. Dez 2013 21:50 Titel: NikolasGauß Verfasst am: 17. Dez 2013 21:50 Titel: |
 |
|
|
Ich weiss leider nicht wie ich auf deine Formel komm, kannst du mir einen Ansatz geben ? Und wieso das machbar ist ? |
|
 |
NikolasGauß
Gast
|
 NikolasGauß Verfasst am: 17. Dez 2013 22:16 Titel: NikolasGauß Verfasst am: 17. Dez 2013 22:16 Titel: |
 |
|
Mir ist gerade etwas aufgefallen. Die Integrationsformel geht ja wie folgt I=Integral r^2 * Massenverteilung(r)dV=Integral r^2 * p(r)dV
Bei der gegebenen Aufgabe ist nur die Dichte p gegeben. Kann es sein das die Massenverteilung p(r) und die Dichte p zwei komplett unterschiedliche Dinge sind ? Den dann wären meine Überlegungen vollkommen falsch (was sie auch sowieso wären denke ich xD) |
|
 |
NikolasGauß
Gast
|
 NikolasGauß Verfasst am: 17. Dez 2013 22:21 Titel: NikolasGauß Verfasst am: 17. Dez 2013 22:21 Titel: |
 |
|
|
Ich sehe gerade das deine genannte Formel auch mehr oder weniger bei Wikipedia steht. Das scheint anscheinend ein Speziallfall des Trägheitsmoments rotationssymmetrischer Körper zu sein. Ein Denkanstoß für eine Herleitung wäre trotzdem super! mfg |
|
 |
DeltaX
Anmeldungsdatum: 24.11.2013
Beiträge: 24
|
 DeltaX Verfasst am: 17. Dez 2013 22:39 Titel: DeltaX Verfasst am: 17. Dez 2013 22:39 Titel: |
 |
|
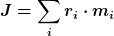
(dein I ist bei mir das J)
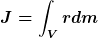
Jetzt nur noch schauen wie 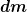 definiert bzw. anders schreibbar ist. definiert bzw. anders schreibbar ist. |
|
 |
NikolasGauß
Gast
|
 NikolasGauß Verfasst am: 17. Dez 2013 22:54 Titel: NikolasGauß Verfasst am: 17. Dez 2013 22:54 Titel: |
 |
|
Guten Abend und danke für die Mühsamkeit!
Ich kenne das Trägheitsmoment noch wie folgt:

Was ist aber jetzt zu machen ? Das roh darf ich ja nicht rausziehen oder ? Da es schleißlich eine variable r enthält. Vielleicht meinst du aber uch etwas komplett anderes. |
|
 |
DeltaX
Anmeldungsdatum: 24.11.2013
Beiträge: 24
|
 DeltaX Verfasst am: 17. Dez 2013 23:08 Titel: DeltaX Verfasst am: 17. Dez 2013 23:08 Titel: |
 |
|
Nönö, deine Gleichung ist fast schon so, wie man sie braucht.
Deine Integrationsvariable soll r sein, also benötigen wir statt dem dV ein dr.
Das Volumen eines Zylinders ist:
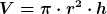
Bei uns ist V dann also:
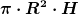
Bilde mal 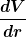 und forme um. und forme um.
So erhältst ein dV was du in die obere Gleichung einsetzen kannst und bist nur noch von r abhängig. |
|
 |
DeltaX
Anmeldungsdatum: 24.11.2013
Beiträge: 24
|
 DeltaX Verfasst am: 17. Dez 2013 23:18 Titel: DeltaX Verfasst am: 17. Dez 2013 23:18 Titel: |
 |
|
Achso, alternativ, falls es dir leichter fallen sollte, kannst du das dV auch über die Zylinderkoordinaten herleiten:
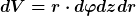
Da musst du dann natürlich aber nicht nur über r integrieren  Ist aber nicht weiter schlimm, wenn du die Grenzen für einen Zylinder kennst. Ist aber nicht weiter schlimm, wenn du die Grenzen für einen Zylinder kennst. |
|
 |
NikolasGauß
Gast
|
 NikolasGauß Verfasst am: 17. Dez 2013 23:23 Titel: NikolasGauß Verfasst am: 17. Dez 2013 23:23 Titel: |
 |
|
Mich würde interessieren woher der Ansatz mit dr kommt ...
Das ist doch normale Substitution oder? Ich würde wie gesgat nicht draufkommen und bin deshalb etwas verwirrt.
Mithilfe V=pi*r^2 *h folgt
dV/dr=2*pi*h*r äquivalent zu dV=2*pi*h*r*dr |
|
 |
DeltaX
Anmeldungsdatum: 24.11.2013
Beiträge: 24
|
 DeltaX Verfasst am: 17. Dez 2013 23:38 Titel: DeltaX Verfasst am: 17. Dez 2013 23:38 Titel: |
 |
|
Der "Ansatz" mit dr kommt daher, da wir uns die Rechnung versuchen zu vereinfachen. Mit Zylinderkoordinaten kommt man auf das gleiche Ergebnis.
Wir haben ein Volumenintegral kennen aber die Volumenelemente dV nicht und außerdem wenn wir ohne Zylinderkoordinaten rechnen, ergeben sich nicht allzuschöne Komponenten über die wir integrieren, was auch daran liegt, dass wir in 3 Dimensionen arbeiten und zunächst im karthesischen Koordinatensystem sind. Runde Anordnungen im karth. Koordsys. sind recht hässlich, weshalb man oft zu eben genannten Zylinderkoord. greift.
Allerdings ist es uns möglich, anstatt über infinitesimale Volumenelemente, mit dem Radius r zu rechnen. Der radius wächst nämlich linear an und ist für eine Teil-Kreischeibe im Zylinder konstant, das hilft viel.
Wir können natürlich nicht einfach das dV durch ein dr ersetzen.
Daher müssen wir das dr aus unserem dV erzeugen.
Wenn wir das Volumen V kennen, ist das Differenzieren nach r auf beiden Seiten eine Äquivalenzumformung und erlaubt uns unser dV zu substituieren.
Und ist dies getan, müssen wir nur noch über r integrieren.
Zu deiner 2. Bemerkung. Das Rho darfst du natürlich nicht vor das Integral ziehen, aber du darfst es natürlich einsetzen.
Du wirst im Integral nach dem Einsetzen wieder nur eine Abhängigkeit von r haben und kannst leicht integrieren.
Dann bist du fast fertig.
Setze also zunächst dein dV und dann dein Rho ein.
Poste dein Ergebnis. |
|
 |
NikolasGauß
Gast
|
 NikolasGauß Verfasst am: 18. Dez 2013 00:00 Titel: NikolasGauß Verfasst am: 18. Dez 2013 00:00 Titel: |
 |
|
Ich bin jetzt etwas unsicher. Mein Problem liegt gerade bei folgendem:
Bei der Aufgabe ist der Radius R und es gilt p(r), dann gilt doch I=20*pi*Integral p*R^2 dR, wobei die Integrationsgrenze 0 bis R ist und ich r als konstante jediglich betrachte, da ich ja nach R integrier.
Hier bin ich mir etwas unsicher. Bei dV/dr wird doch der Radius r vom Körper gemeint oder? Ich hoffe das ist verständlich und das Problem ist nachvollziehbar. Es ist halt auf die Aufgabe bezogen...  |
|
 |
DeltaX
Anmeldungsdatum: 24.11.2013
Beiträge: 24
|
 DeltaX Verfasst am: 18. Dez 2013 00:10 Titel: DeltaX Verfasst am: 18. Dez 2013 00:10 Titel: |
 |
|
Zunächst ist in der Formel 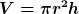 das Volumen eines allgemeinen Zylinders gemeint, also ist r noch variabel. das Volumen eines allgemeinen Zylinders gemeint, also ist r noch variabel.
Auch bei 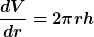 bleibt das r dann natürlich weiterhin variabel. Wir betrachten ja immer Teilvolumina eines Zylinders mit dem Radius r. bleibt das r dann natürlich weiterhin variabel. Wir betrachten ja immer Teilvolumina eines Zylinders mit dem Radius r.
Wenn wir unser neues dV nun im Integral substituieren ergibt sich ein Integral von 0 bis R :
\cdot r^2 2 \pi r h dr =\int _0^R \rho (r) \cdot r^3 2 \pi h dr )
Der "echte" Zylinderradius wird also erst beim Auflösen des Integrals eingesetzt.
Jetzt bist du dran. |
|
 |
NikolasGauß
Gast
|
 NikolasGauß Verfasst am: 18. Dez 2013 00:30 Titel: NikolasGauß Verfasst am: 18. Dez 2013 00:30 Titel: |
 |
|
|
Ich komme auf 0,266 kgm^2 etwa. Ist das richtig ? |
|
 |
DeltaX
Anmeldungsdatum: 24.11.2013
Beiträge: 24
|
 DeltaX Verfasst am: 18. Dez 2013 00:54 Titel: DeltaX Verfasst am: 18. Dez 2013 00:54 Titel: |
 |
|
Schreib mal bitte deine Rechenschritte auf.
Also
i) das Integral mit eingesetzem dV.
ii) das Integral von i) mit Rho(r) eingesetzt.
iii) die Stammfunktion des Integrals.
Ich habe nämlich einen anderen Wert heraus.
Edit:// An dem Rechenweg können wir ja etwaige Fehler sehen, ich hab leider keine Zeit (gehabt) die vollständige Rechnung zu machen, also kann sich's bei mir auch um einen Faktorfehler handeln. Gleiches ist auch bei dir möglich. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 18. Dez 2013 11:02 Titel: GvC Verfasst am: 18. Dez 2013 11:02 Titel: |
 |
|
| NikolasGauß hat Folgendes geschrieben: | | Ich komme auf 0,266 kgm^2 etwa. Ist das richtig ? |
Nein. Außerdem fordert die Aufgabenstellung etwas Anderes:
| Zitat: | | Geben Sie das Ergebnis in Abhängigkeit von der Masse an. |
|
|
 |
NikolasGauß
Gast
|
 NikolasGauß Verfasst am: 18. Dez 2013 12:04 Titel: NikolasGauß Verfasst am: 18. Dez 2013 12:04 Titel: |
 |
|
Guten Morgen! Ich habe mich noch einmal mit der Umschreibung beschäftigt und denke das ich es jetzt zu 80%-90% verstehe, zumindest mithilfe der Zylinderkoordinatenschreibweise! Ich werde das Integral gleich noch einmal lösen. Aber eine Frage vorweg:
,,Geben Sie das Ergebnis in Abhängigkeit von der Masse an."
Muss ich das bereits vor der Integration beachten oder nach der Integration ? Hier muss ich sicher für irgendeine Variable einen Zusammenhang mit der Masse m finden. |
|
 |
DeltaX
Anmeldungsdatum: 24.11.2013
Beiträge: 24
|
 DeltaX Verfasst am: 18. Dez 2013 12:25 Titel: DeltaX Verfasst am: 18. Dez 2013 12:25 Titel: |
 |
|
*Mehrere Konstanten
Die Masse des Zylinders ist ja nicht variabel.
Löse das Integral und vereinfache. (Tipp: Wenn du ein 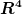 bei der Lösung erhältst, ist es für die Aufgabenstellung nötig es in bei der Lösung erhältst, ist es für die Aufgabenstellung nötig es in 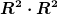 aufzuteilen. Dann siehst Du auch, was mit der Masse gemeint ist.) aufzuteilen. Dann siehst Du auch, was mit der Masse gemeint ist.) |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 18. Dez 2013 13:13 Titel: GvC Verfasst am: 18. Dez 2013 13:13 Titel: |
 |
|
Die Aufgabenstellung
| Zitat: | | Geben Sie das Ergebnis in Abhängigkeit von der Masse an. |
fordert Dich vor allen Dingen dazu auf, mit allgemeinen Größen zu rechnen und alle gegebenen Zahlenwerte erstmal außen vor zu lassen, da sie nur Verwirrung stiften und den Blick auf das Wesentliche verschleiern.
| NikolasGauß hat Folgendes geschrieben: | | Muss ich das bereits vor der Integration beachten oder nach der Integration ? |
Nach der Integration. Du hast das Trägheitsmoment zu bestimmen und anschließend zu schauen, welcher darin enthaltene Ausdruck die Masse des Zylinders kennzeichnet.
Dein Hauptproblem scheint weniger im Verständnis, als vielmehr in Deiner Vorstellungskraft zu bestehen. Du hast einen Zylinder, dessen Dichte sich mit dem Radius ändert.
^2\right))
An der Stelle r=0 ist die Dichte nach dieser Gleichung gerade 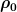 . An der Stelle r=R ist sie . An der Stelle r=R ist sie 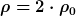 . Die Frage ist nun, wie die Masse eines solchen Zylinders zu berechnen ist. Wenn Du das begriffen hast, ist auch die Berechnung des Trägheitsmomentes kein Problem mehr, denn dort liegt dieselbe Vorstellung zugrunde. . Die Frage ist nun, wie die Masse eines solchen Zylinders zu berechnen ist. Wenn Du das begriffen hast, ist auch die Berechnung des Trägheitsmomentes kein Problem mehr, denn dort liegt dieselbe Vorstellung zugrunde.
Sicher ist doch, dass bei nicht konstanter Dichte das gesamte Volumen in infinitesimal kleine Teilvolumina dV zu unterteilen ist. Von diesen Teilvolumina wird die jeweilige infinitesimal kleine Masse dm bestimmt. Um die Gesamtmasse zu erhalten, müssen alle Teilmassen aufaddiert werden. Die Addition infinitesimal kleiner Elemente nennt man Integration.
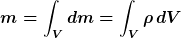
Da 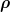 in Abhängigkeit von r gegeben ist, müssen jetzt infinitesimal kleine Volumina dV gefunden werden, in denen r praktisch konstant ist (denn sonst kannst Du die Dichte nicht angeben) und deren Gesamtheit das gesamte Zylindervolumen ergeben. Diese infinitesimal kleinen Teilvolumina können nach dieser Vorgabe nur aus infinitesimal dünnen Zylinderschalen bestehen, die wie die Schichten einer Porreestange ineinandergeschichtet sind. (Ich weiß, dass ich mit diesem Gemüsevergleich die mathematischen Gefühle manch eines an diesem Forum beteiligten Physikers verletze, lasse es aber darauf ankommen, da nach meiner Erfahrung diese Vorstellung schon so manchem Studienanfänger sehr geholfen hat). in Abhängigkeit von r gegeben ist, müssen jetzt infinitesimal kleine Volumina dV gefunden werden, in denen r praktisch konstant ist (denn sonst kannst Du die Dichte nicht angeben) und deren Gesamtheit das gesamte Zylindervolumen ergeben. Diese infinitesimal kleinen Teilvolumina können nach dieser Vorgabe nur aus infinitesimal dünnen Zylinderschalen bestehen, die wie die Schichten einer Porreestange ineinandergeschichtet sind. (Ich weiß, dass ich mit diesem Gemüsevergleich die mathematischen Gefühle manch eines an diesem Forum beteiligten Physikers verletze, lasse es aber darauf ankommen, da nach meiner Erfahrung diese Vorstellung schon so manchem Studienanfänger sehr geholfen hat).
Das Volumen einer "Porreeschicht" mit der infinitesimal kleinen Dicke dr ist aus der Vorstellung heraus sofort anzugeben. Denn ihre Grundfläche ist
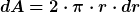
und ihr Volumen bei vorgegebener Höhe h deshalb
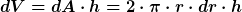
Demzufolge ist ihre Masse
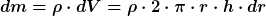
Wenn jetzt noch die gegebene Dichte eingesetzt und alles ein bisschen geordnet wird, erhält man
^2\right)\cdot dr)
Ausmultiplizieren:
\cdot dr)
Dieser Ausdruck lässt sich nun problemlos sowohl in das Integral für die Massenbestimmung als auch in das für die Bestimmung des Trägheitsmomentes einsetzen:
\, dr)
und
\, dr=\rho_0\cdot 2\cdot\pi\cdot h\cdot\int_0^R \left(r^3+\frac{r^5}{R^2}\right)\, dr)
Das auszurechnen sollte jetzt keine Schwierigkeit mehr darstellen, oder? |
|
 |
NikolasGauß
Anmeldungsdatum: 18.12.2013
Beiträge: 1
|
 NikolasGauß Verfasst am: 18. Dez 2013 14:36 Titel: NikolasGauß Verfasst am: 18. Dez 2013 14:36 Titel: |
 |
|
Die Integration über nur dr macht mich wirklich sehr verwirrend. Ich werde dieses Verfahren mir am Wochenende noch einmal anschauen, versprochen! Ich hab jetzt bisschen überlegt und mich mit den Zylinderkoordinaten auseinander gesetzt. Dabei komm ich letztendlich auf folgendes Integral (Siehe Anhang). Wenn ich das nun löse, dann sollte dies gleich dem Integral wie von dir das genannte sein oder ? Kann ich jetzt ersteinmal das Integral normal lösen?
Edit1// Ich weiss nicht wieso das Bild so groß ist. Es sollte eigentlich im Normalverhältnis sein. Tut mir leid, aber irgendetwas ist schief gelaufen! Ich werde es nochmal neuhochladen!
Edit2// ^{2}) r^{3} \, dzdrdd\phi)
Dieses Integral bekomme ich mithilfe Zylinderkoordinaten herraus. Kann ich das nun ganz normal mit den bekannten Regeln des mehrfachintegrals integrieren ? |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 18. Dez 2013 16:04 Titel: GvC Verfasst am: 18. Dez 2013 16:04 Titel: |
 |
|
| NikolasGauß hat Folgendes geschrieben: | | Die Integration über nur dr macht mich wirklich sehr verwirrend. |
Dann hast Du meinen Beitrag entweder nicht gelesen oder überhaupt nicht verstanden.
| NikolasGauß hat Folgendes geschrieben: | | Dieses Integral bekomme ich mithilfe Zylinderkoordinaten herraus. Kann ich das nun ganz normal mit den bekannten Regeln des mehrfachintegrals integrieren ? |
Wenn Du das unbedingst willst, dann mach' es. Ich wollte nur helfen und Deiner Vorstellungskraft auf die Sprünge helfen. Physik ist nicht Mathematik, sondern wird durch die Mathematik nur beschrieben. Wenn Du Dich mit der Physik beschäftigst, solltest Du ein gegebenes physikalisches Szenario zuerst verstehen. Erst dann kannst Du die Mathematik bemühen, die das Szenario beschreibt.
Warum willst Du unbedingt ein Mehrfachintegral lösen, wenn die zu integrierende Größe ausschließlich von einer Variablen (hier vom Radius r) abhängt? Die Dichte ist doch für jedes beliebige z und für jedes beliebige  konstant, sofern Du r konstant lässt. Diese Tatsache führt Dich doch sofort und unmittelbar dazu, anstelle des Volumenelementes konstant, sofern Du r konstant lässt. Diese Tatsache führt Dich doch sofort und unmittelbar dazu, anstelle des Volumenelementes
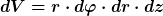
das Volumenelement
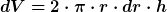
zu betrachten und anstelle des Mehrfachintegrals das einfachere Integral über r zu berechnen. Denn für dieses Element ("Porreeschicht") kannst Du sofort und ohne Weiteres die zugehörige infinitesimal kleine Masse angeben (siehe meinen vorigen Beitrag). Natürlich kommt in beiden Fällen dasselbe raus.
Wie Du allerdings auf ein vernünftiges Ergebnis kommen willst, wenn Du mit Zahlenwerten operierst und die Einheiten der physikalischen Größen ignorierst, wundert mich. Merke: Physikalische Rechnungen ohne Einheiten sind keine. Außerdem: Wie willst Du dann die eigentliche Aufgabe, nämlich das Trägheitsmoment in Abhängigkeit von der Masse anzugeben, lösen?
Also noch einmal: Berechnungen in der Physik erfolgen zunächst erstmal mit allgemeinen Größen. Zahlenwerte und Einheiten werden erst eingesetzt, wenn Du das Ergebnis in allgemeiner Form vorliegen hast. Alles andere verstellt Dir den Blick auf die eigentliche Physik.
Ob Du das Ergebnis nun mit Hilfe des Mehrfach- oder des Einfachintegrals ermittelst, ist dabei vollkommen egal. |
|
 |
NikolasGauß1
Gast
|
 NikolasGauß1 Verfasst am: 18. Dez 2013 18:10 Titel: NikolasGauß1 Verfasst am: 18. Dez 2013 18:10 Titel: |
 |
|
Hallo, ich komme auf folgendes Ergebnis:

Ist das richtig oder noch einmal nachrechnen ? |
|
 |
NikolasGauß1
Gast
|
 NikolasGauß1 Verfasst am: 18. Dez 2013 18:20 Titel: NikolasGauß1 Verfasst am: 18. Dez 2013 18:20 Titel: |
 |
|
|
Edit: Hab dein genanntes Integral berechnet, kommt anscheinend dasselbe herraus auf, dass du ein kleines h verwendest und ich ein großes h. Ich glaube mit dem großen H ist es laut Aufgabenstelung richtig wie ich es nenne oder? |
|
 |
NikolasGauß1
Gast
|
 NikolasGauß1 Verfasst am: 18. Dez 2013 19:17 Titel: NikolasGauß1 Verfasst am: 18. Dez 2013 19:17 Titel: |
 |
|
|
Wenn ich nun das Trägheitsmoment im Zusammenhang der Masse bestimmen soll, dann gibt es hier doch nur die Möglichkeit po=m/V0 zu verwenden? Sofern mein berechnetes Allgemeines Trägheitmsmoment bisher richtig ist. |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 18. Dez 2013 19:49 Titel: as_string Verfasst am: 18. Dez 2013 19:49 Titel: |
 |
|
Hallo,
zwar stimmt Dein Ergebnis für das Trägheitsmoment schon, allerdings frag ich mich, wie Du so was rechnest: Aus dem Integral würde ich ja erstmal alle Konstanten nach vorne ziehen. Dann sollte man schon das R² weg kürzen und letztlich kann man noch etwas Bruchrechnen anwenden. Dann steht bei mir nur noch:

da. Da kann man auch noch
Jetzt aber zur Masse: Die Formel 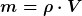 geht nur, wenn die Dichte über das Volumen homogen, also konstant ist. Das ist hier doch ganz offensichtlich nicht der Fall, sonst hätten wir uns ja die Rechnerei mit dem Drehmoment auch sparen können und einfach die Formel für das Drehmoment eines Zylinders nehmen können. geht nur, wenn die Dichte über das Volumen homogen, also konstant ist. Das ist hier doch ganz offensichtlich nicht der Fall, sonst hätten wir uns ja die Rechnerei mit dem Drehmoment auch sparen können und einfach die Formel für das Drehmoment eines Zylinders nehmen können.
GvC (und wahrscheinlich auch andere) hat ein paar Posts weiter oben schon sehr schön das alles (auch mit der Masse) ausführlich erklärt, wie man auf die Masse kommt und dass man sehr ähnlich integrieren muss, nur eben, dass der Faktor r² im Integral weg fällt. Schau Dir erst nocheinmal seinen Post an, bitte. Noch mehr Wiederholungen können das auch nicht besser machen...
Gruß
Marco |
|
 |
NikolasGauß1
Gast
|
 NikolasGauß1 Verfasst am: 18. Dez 2013 20:39 Titel: NikolasGauß1 Verfasst am: 18. Dez 2013 20:39 Titel: |
 |
|
Den einzigen Ansatz, den ich jetzt wahrgenommen habe ist mein berechnetes Trägheitsmoment ersteinmal komplett zusammenzufassen und danach m=Integral p dV zu berechnen. Danach kann ich hoffen, nach dem ich m=Integral p dV berechnet habe, derselbe Term bei meinemTrägheitsmoment vorkommt um diesen Term ebend mit m zu ersetzen.
Ist der Gedanke richtig? |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 18. Dez 2013 20:47 Titel: as_string Verfasst am: 18. Dez 2013 20:47 Titel: |
 |
|
Ja, das klingt sehr gut! 
Wie sieht das Integral für die Masse in diesem konkreten Fall dann aus? Kannst Du das aus den bisherigen Tipps schon ableiten?
Gruß
Marco |
|
 |
NikolasGauß1
Gast
|
 NikolasGauß1 Verfasst am: 18. Dez 2013 21:06 Titel: NikolasGauß1 Verfasst am: 18. Dez 2013 21:06 Titel: |
 |
|
Ich komme nun auf folgende Ergebnisse:

Und Analog 
Jetzt fass ich beides zusammen und vermute mal, dass ich dann m einsetzten kann. Werd es ausprobieren. |
|
 |
NikolasGauß1
Gast
|
 NikolasGauß1 Verfasst am: 18. Dez 2013 21:23 Titel: NikolasGauß1 Verfasst am: 18. Dez 2013 21:23 Titel: |
 |
|
ich komme letztendlich auf:
I=p0*H*2pi*((5R^4)/(12))
und
m=p0*H*2pi*((3R^2)/(4))
Das sieht nicht nach demselben Trägheitsmoment wie deinem aus .. Bei I kann ich nun R^4=R^2 * R^2 umschreiben. Aber die 3/4 die bekomm ich da irgendwie nicht herraus.
Mein Ergebnis sollte auch richtig sein, gekürzt habe ich auch maximal. |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 18. Dez 2013 22:13 Titel: as_string Verfasst am: 18. Dez 2013 22:13 Titel: |
 |
|
Hallo!
Wieso, ist doch identisch! Du hast halt die 2 von den 2 pi noch nicht gegen die 12 gekürzt, was auch ok ist... Aber sonst.
Die Aufgabe war ja, das I in Abhängigkeit von m darzustellen. Schau Dir mal die Trägheitsmoment z. B. auf der Wikipedia-Seite an (für verschiedene Körper mit homogener Masseverteilung). Da ist z. B. das für einen Vollzylinder: 1/2 m R² oder andere. Bei all diesen Beispielen ist immer noch ein m als Faktor mit drin.
Du sollst Dein Trägheitsmoment jetzt auch in der Form I= Faktor mal m darstellen. Am einfachsten machst Du das, indem Du mal I/m ausrechnest. Dieses Ergebnis wäre ja gerade dieser Faktor!
Gruß
Marco |
|
 |
NikolasGauß1
Gast
|
 NikolasGauß1 Verfasst am: 18. Dez 2013 22:23 Titel: NikolasGauß1 Verfasst am: 18. Dez 2013 22:23 Titel: |
 |
|
Abend und vielen Dank für die Hilfe! Ich muss gestehen, dass ich selbst niemals draufkommen würde I/m zu berechnen. Wie kommt man den hierdrauf? Ich habe mir ebend jegliche Formeln der Translation angeschaut aber einen Zusammenhang scheine ich nicht zu finden.
mfg |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 18. Dez 2013 22:30 Titel: as_string Verfasst am: 18. Dez 2013 22:30 Titel: |
 |
|
Naja, von den Einheiten des Trägheitsmomentes ist es irgendwie schon nahe liegend.
Dann, wenn man die Ergebnisse anschaut: Da ist jeweils eine reine Zahl, ein rho_0, ein pi und "ein paar R". Dass da einiges weg fällt, wenn man das eine durch das andere teilt, ist vielleicht auch ein Hinweis.
Gruß
Marco |
|
 |
NikolasGauß1
Gast
|
 NikolasGauß1 Verfasst am: 18. Dez 2013 22:34 Titel: NikolasGauß1 Verfasst am: 18. Dez 2013 22:34 Titel: |
 |
|
So, ich komme auf I=(5/9)R^2 * m
Das sieht sehr richtig aus, wenn man die anderen Trägheitsmomente vergleicht. Trotzdem würde ich nie auf die Idee kommen beides ins Verhältnis zu setzen, also die eine Gleichung durch die andere Gleichung zu berechnen. |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 18. Dez 2013 22:41 Titel: as_string Verfasst am: 18. Dez 2013 22:41 Titel: |
 |
|
| NikolasGauß1 hat Folgendes geschrieben: | So, ich komme auf I=(5/9)R^2 * m
Das sieht sehr richtig aus, wenn man die anderen Trägheitsmomente vergleicht. Trotzdem würde ich nie auf die Idee kommen beides ins Verhältnis zu setzen, also die eine Gleichung durch die andere Gleichung zu berechnen. |
Ja, das hab ich auch raus! Sehr gut! 
Das stimmt, wenn man das z. B. mit dem eines normalen Vollzylinder mit homogener Massenverteilung vergleicht, ist der Vorfaktor 1/2 ja nur etwas kleiner als unsere 5/9. Und das ist auch das erwartete Ergebnis: Die Dichte wächst ja nach außen hin an, so dass "im Mittel" die Masse eher im Außenbereich sich verteilt, als bei einem Vollzylinder. Dann sollte auch das Trägheitsmoment im Vergleich zur Masse größer werden.
Vielleicht kommt man auch eher auf die Idee, wenn man mal schon ab und zu ein paar Trägheitsmomente ausgerechnet hat. Wenn man homogene Körper hat, bekommt man oft irgendwo einen Faktor "Gesamtvolumen mal Dichte". Dann ist es ja offensichtlich, dass das der Masse entsprechen muss. Und die schreibt man dann häufig auch extra hin, so wie es bei den Beispiel-Trägheitsmomenten auf Wikipedia auch der Fall ist.
Gruß
Marco |
|
 |
NikolasGauß1
Gast
|
 NikolasGauß1 Verfasst am: 18. Dez 2013 22:47 Titel: NikolasGauß1 Verfasst am: 18. Dez 2013 22:47 Titel: |
 |
|
Danke nochmals!
Obwohl, gerade im nachhinein wenn man sich die ganzen Formeln anschaut sieht man ja das J=0,5mr^2 ist, was ja äquivalent J/m=0,5r^2 ist. Und das Verhältnis J/m gilt für alle Körper anscheinend. Hab es mir nun gut eingeprägt! |
|
 |
NikolasGauß1
Gast
|
 NikolasGauß1 Verfasst am: 18. Dez 2013 23:07 Titel: NikolasGauß1 Verfasst am: 18. Dez 2013 23:07 Titel: |
 |
|
Ich würde noch gerne die letzte Teilaufgabe bitte lösen, wobei ich hier eigentlich nur ein Problem habe:
Wie lange braucht der Zylinder, um auf einer schiefen Ebene mit dem Neigungswinkel� @= 10◦ aus einer Höhe von h = 1m herabzurollen
Meine Idee ist Epot=Ekin+Erot (Bewegungsenergie setzt sich zusammen aus Rotationsenergie und kinetischer Energie) Ich bin mir aber unsicher ob ebend Ekin + Erot gilt oder nur Erot.. |
|
 |
Namenloser324
Gast
|
 Namenloser324 Verfasst am: 18. Dez 2013 23:15 Titel: Namenloser324 Verfasst am: 18. Dez 2013 23:15 Titel: |
 |
|
Ekin + Erot ist richtig. (bzw. man kann es auch als reine Rotiation betrachtet die zu jedem Zeitpunkt t ihr rotationszentrum ändert, dann hätte man nur rotationsenergie)
E_rot ist die reine Rotationsenergie und ekin die kinetische Energie des Schwerpunktes |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
 as_string Verfasst am: 18. Dez 2013 23:19 Titel: as_string Verfasst am: 18. Dez 2013 23:19 Titel: |
 |
|
Wobei man glaube ich normalerweise eher sagt: die Kinetische Energie ist beides zusammen und setzt sich deshalb aus Translations- und Rotations-Energie zusammen. Deine Kinetische würde man dann also eher Translations-Energie nennen.
So weit kenne ich die Begriffe zumindest. Bin mir da aber auch nie so ganz sicher... 
Gruß
Marco |
|
 |
NikolasGauß1
Gast
|
 NikolasGauß1 Verfasst am: 18. Dez 2013 23:48 Titel: NikolasGauß1 Verfasst am: 18. Dez 2013 23:48 Titel: |
 |
|
Danke, dann scheint das zu stimmen. Ich bin mir gerade aber aufeinmal wieder etwas unsicher. Ich soll ja die Zeit bestimmen in dem der Zylinder bei Punkt 2 ankommt. Die Strecke kann ich ja berechnen mithilfe h=s*sin@, h und der Neigungswinkel sind ja schließlich gegeben.
Jetzt brauch ich noch sicher die Winkelgeschwindigkeit. Ich könnte für Ekin v ersetzten durch Winkelgeschwindigkeit*r (Bahngeschwindigkeit). Dann sind eigentlich nur Translationseigenschaften gegeben. Das Trägheitsmoment könnte ich ebenfalls ersetzen durch meine bei a berechneten Trägheitsmoment. Nun nach der Winkelgeschwindigkeit auflösen (also Epot=Ekin+Erot) und dann habe ich letztendlich die Winkelgeschwindigkeit.
Daraufhin kann ich mithilfe Zeit=Winkelweg/Winkelgeschwindigkeit die Aufgabe letztendlich lösen.
Ist das richtig so? Ist ,,Winkelweg"=Strecke s exakt ? |
|
 |
|
















 Ist aber nicht weiter schlimm, wenn du die Grenzen für einen Zylinder kennst.
Ist aber nicht weiter schlimm, wenn du die Grenzen für einen Zylinder kennst.

