| Autor |
Nachricht |
Das Original
Gast
|
 Das Original Verfasst am: 10. Jan 2006 16:38 Titel: Trägheitsmoment Quader Integral Das Original Verfasst am: 10. Jan 2006 16:38 Titel: Trägheitsmoment Quader Integral |
 |
|
gute tag erstmal 
also ich hba ehier irgendwie anscheinen eine integral rechung. aber irgendwie habe ich mich noch nicht damit so richtig angefreundet, in der Physik mit integralen zu rechnen. fazit: ich blicke da ehrlich noch nicht so richtig durch. darum bin ich zu euch gekommen, um mir ein bisschen hilfe zu holen. wenn es für euch ok ist 
Hier die aufgabe, die ein bisschen seltsam ist:
Berechnen Sie das Trägheitsmoment von einem Quader der Masse m mit den Seitenlängen a,b und c. Der Quader soll sich um eine Achse drehen, die durch seinen Schwerpunkt geht und senkrecht auf der von a und b gebildeten Fläche steht.
Hinweis, legen Sie den Schwerpunkt des Quaders in den Ursprung eines kartesischen Koordinatensystems wobei die Kante mit der Länge a parallel zur x-Achse liegt und die Kante mit der Seitenlänge b parallel zu y Achse. Die Drehung erfolgt dann um die z-Achse.
Mehrdimensionale Integrale kann man berechnen, indem man sie in beliebiger Reihenfolge in
Integrale über die einzelnen Koordinaten aufspaltet und nacheinander berechnet:
   dxdy = \int \left( \int f (x,y) dx\right) dy)
ehrlich, ich verstehe nur bahnhof  . .
kann jemand mit der aufgabe was anfangen? wenn es da jemand gibt, dann hochachtung 
aufjedenfall schonmal danke für tipps ,anregungen und hilfen |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 10. Jan 2006 17:00 Titel: as_string Verfasst am: 10. Jan 2006 17:00 Titel: |
 |
|
Wo genau hast Du Schwierigkeiten? Wie man solche Integrale im Prinzip rein mathematisch löst? Oder wie man auf das Integral überhaupt erst kommt, wenn man ein Trägheitsmoment ausrechnen will?
Gruß
Marco |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 10. Jan 2006 17:07 Titel: as_string Verfasst am: 10. Jan 2006 17:07 Titel: |
 |
|
Ok, vielleicht schreib ich doch schon mal etwas mehr:
Das Trägheitsmoment bezüglich einer Achse ist so definiert:
 \cdot \text{d}V)
wobei r der Abstand eines Punktes zu der Achse ist.
Verstehst Du das noch?
Wenn ja wäre die nächste Frage: Verstehst Du, warum das zweite Integral eigentlich mehrere Integrale sind (weil man eben über ein Volumen integriert)?
Wenn Du das auch noch verstehst, dann wäre der nächste Punkt: Wie löst man solche Mehrfachintegrale auf?
Wenn Du uns genauer sagst, wo wir anfangen sollen, ist das besser. Es ist nicht wirklich sinnvoll hier ne Komplette Herleitung von Trägheitsmomenten inklusive Integralrechnung zu schreiben und sicher auch nicht nötig, weil Du ja bestimmt ein paar Sachen (zumindest ansatzweise) schon kapiert hast, ohne es vielleicht selbst zu wissen!
Gruß
Marco |
|
 |
Das Original
Gast
|
 Das Original Verfasst am: 10. Jan 2006 17:16 Titel: Das Original Verfasst am: 10. Jan 2006 17:16 Titel: |
 |
|
ok, vielen dank das du dir schonmal die mühe mit mir machen möchtest 
diese Formel für das Trägheitsmoment, was dui da aufgeschrieben hast, die sagt mir was. also ich habe sie schonmal gesehen. mer leider auch nicht. ich wüsste aber jetzt icht, wie ich das auf die aufgab ewohl beziehen soll. oder alles weiterewas du da aufgeschriben hast, sagt mir auch nicht wirklich viel  . .
es tut mir leid. ich wollte die aufgabe schon liegen lassen. aber so leicht aufgeben möchte ich auch nicht. |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 10. Jan 2006 18:06 Titel: as_string Verfasst am: 10. Jan 2006 18:06 Titel: |
 |
|
OK, immerhin ist es Dir nicht ganz fremd! Das ist doch schonmal ein Anfang. Ich würde vorschlagen, wir machen das vielleicht Schrittweise: Erstmal versuchen wir das (Mehrfach-)Integral zusammen hin zu bekommen! Das dann nachher mathematisch einfach zu lösen ist dann so wie so nicht mehr so interessant 
Also: für unsere Formel mit dem Volumenintegral brauchen wir den Abstand jedes Punktes von der Drehachse. Achso: Da fällt mir ein: Man kann das Volumen auf eine Fläche vereinfachen. Nimm einfach mal an, dass der Quader sehr flach ist, also c ziemlich klein. Das macht nachher nix, weil die Ausdehnung in Richtung der Drehachse für das Drehmoment egal ist. Alle Punkte sind parallel zur Achse ja gleich weit von der Achse entfernt, deshalb kann man die dann zusammen nehmen. (Wenn Du den Punkt jetzt nicht verstehst ist das im Moment nicht ganz so wichtig, häng Dich also erstmal daran nicht zu sehr auf...)
So, jetzt brauchen wir den Abstand eines kleinen Flächenpunktes von der Drehachse. Einen unendlich kleinen Flächenpunkt bezeichnet man dann mit

also ganz kleines x mal ganz kleines y. Stell Dir am besten die Fläche in ganz kleine Quadratchen unterteilt und für jedes einzelne brauchen wir die Entfernung zur Achse, also zum Ursprung in dem Bsp.
Das geht einfach über Pyth.:

Gut, dass in der Formel r^2 vorkommt! So fällt die Wurzel gleich wieder weg! Jetzt aber noch das mit der Dichte Rho: Die Volumendichte ist ja:

Aber man kann auch eine Flächendichte definieren, die uns ausreicht, weil wir ja das ganze auf zwei Dimensionen vereinfacht haben. Das ist dann einfach:

Jetzt kommt der schwierige Schritt das alles zu einem Integral zusammen zu bauen. Die Sache ist jetzt, dass wir die Mini-Trägheitsmomente für jedes einzelne Mini-Flächenstückchen aufaddieren müssen. Und bei unendlich vielen und dafür unendlich kleinen Flächenstückchen ist das halt dann ein Integral (ich denke, dass das der Punkt ist, der Dir am meisten Schwierigkeit macht. Das ist wichtig, dass Du den verstehst! Wenn Du Dir da unsicher bist, dann frag nochmal genauer nach. Erzähl' dabei auch, welche Gedanken Du Dir gemacht hast, wenn sie Dir auch dumm vorkommen. So kann ich/wir Dir am besten helfen...)
 \rho_A \text{d}x \text{d}y)
Ok. Das sieht doch schonmal ganz gut aus...Jetzt mußt Du das erstmal mit x integrieren und dabei y als konstant betrachten und danach das selbe mit y. Aber wichtiger ist erstmal, dass Du den ersten Teil verstehst. Da steckt nämlich die Physik drin. Der Rest ist dann "nur" noch rechnen...
Gruß
Marco
Edit: Sorry! Ich hatte einen Fehler gemacht. Ich bin von Kantenlängen 2a, 2b und 2c ausgegangen... Hab's jetzt aber korrigiert! |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 12. Jan 2006 15:19 Titel: as_string Verfasst am: 12. Jan 2006 15:19 Titel: |
 |
|
Schade... hab' ich Dich jetzt verloren? Ich dachte wir wollten die Aufgabe noch zusammen fertig rechnen?  Alleine bekomme ich das sicher nie hin Alleine bekomme ich das sicher nie hin 
Wie heißt das im Fernsehen? "Bitte melde Dich!" 
Gruß
Marco |
|
 |
Diger_Diga
Anmeldungsdatum: 12.08.2006
Beiträge: 15
|
 Diger_Diga Verfasst am: 07. Dez 2006 18:07 Titel: hallo, Diger_Diga Verfasst am: 07. Dez 2006 18:07 Titel: hallo, |
 |
|
ist zwar schon lange her aber habe selber mal ne frage hoffe da ist noch jemand der mir die beantworten kann!
der punkt ist!!!
trägheitsmomente über kugeln lösen ist ja nicht so das problem (glaub ich)
wenn rho konstant ist kann ich doch schreiben:
rho (integral) 4*pi*r^2 * r^2 * dr oda nicht
wenn rho abhängig ist von r also zum beispiel rho(r) = 10- (r/1000)^2
und das trägheitsmoment (integral) r^2 * dm ist und das volumenintegral (welches ich mir irgendwo mal aufgegriffen habe bzw irgendwoher mal behalten habe) - (integral) 4*pi*r^2 dr dann kann ich doch für mein dm schreiben da dm = (4pi*r^2)*(10 - (r/1000)^2) (abhängig von r)
demnach ist das trägheitsmoment J = (integral) r^2 * (4*pi*r^2)*(10- (r/1000)^2) * dr oder nicht???
ich habe das bis jetzt immer mit unendlichen summen gelöst!
ich hab mir das jedenfalls so selber mal so hergeleitet aber mit integralen hab ich manchmal doch mein problem dann eins aufzustellen!
bei einem quader - was ist denn die funktion eines quaders - also analog zur kugel (integral) 4*pi*r^2 dr |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. Dez 2006 20:49 Titel: dermarkus Verfasst am: 07. Dez 2006 20:49 Titel: |
 |
|
@Diger_Diga:
Wie das Volumenintegral aussieht, das du beim Berechnen eines Trägheitsmomentes bekommst, hängt von den Koordinaten ab, die du in der Berechnung verwendest.
Das Trägheitsmoment für einen Körper mit homogener Dichte 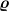 ist: ist:

Dabei ist r der Abstand des jeweiligen Volumenelementes dV von der Rotationsachse.
Für einen Quader mit den Seitenlängen a, b und c kann man in kartesischen Koordinaten x, y und z rechnen. Da ist das Volumenelement

und wenn die Drehachse durch den Mittelpunkt des Quaders geht und in z-Richtung zeigt, dann ist

Für das Trägheitsmoment erhält man also folgendes Dreifachintegral:
 \varrho \, \dd x \, \dd y \, \dd z )
Wie du siehst, stehen hier bei dieser Berechnung in kartesischen Koordinaten gar keine zusätzlichen Faktoren von  und keine Faktoren von und keine Faktoren von 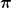 mit im Integral. mit im Integral.
--------------------------------------------------------
Faktoren von 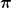 oder zusätzliche Faktoren von r bekommt man nur dann in dem Integral, wenn man das Trägheitsmoment für runde Körper ausrechnen möchte und dafür zum Beispiel Zylinderkoordinaten verwendet. Dann muss man also dementsprechend das Volumenelement in Zylinderkoordinaten verwenden. oder zusätzliche Faktoren von r bekommt man nur dann in dem Integral, wenn man das Trägheitsmoment für runde Körper ausrechnen möchte und dafür zum Beispiel Zylinderkoordinaten verwendet. Dann muss man also dementsprechend das Volumenelement in Zylinderkoordinaten verwenden.
// edit: Stimmt, in der Formel für das J unten hatte ich noch das rho vergessen. Ich habe das nun korrigiert.
Zuletzt bearbeitet von dermarkus am 07. Dez 2006 23:36, insgesamt einmal bearbeitet |
|
 |
Diger_Diga
Anmeldungsdatum: 12.08.2006
Beiträge: 15
|
 Diger_Diga Verfasst am: 07. Dez 2006 22:34 Titel: Diger_Diga Verfasst am: 07. Dez 2006 22:34 Titel: |
 |
|
das fehlt noch dein rho in der formel !
naja mathematisch ist das ja alles kein problem aber anschaulich blick ich durch die integral darstellung noch nicht ganz durch ich schreib sowas wie gesagt immer als summe zum beispiel bei einer kugel hab ich das so gemacht. kam mir viel logischer vor!
^2 \cdot 2 \cdot \sqrt{R^2-(i \cdot R/n)^2}-(((i-1) \cdot R/n)^2) \cdot 2 \cdot \sqrt{R^2-(i \cdot R/n)^2})\cdot (i \cdot R/n)^2 \right])
irgendwie funktioniert der formeleditor net bei mir
[doch, tut er - wenn man den syntax beachtet ;-) .. hier gibt's ein paar erklärungen, para] |
|
 |
Diger_Diga
Anmeldungsdatum: 12.08.2006
Beiträge: 15
|
 Diger_Diga Verfasst am: 07. Dez 2006 23:25 Titel: Diger_Diga Verfasst am: 07. Dez 2006 23:25 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: | @Diger_Diga:
Wie das Volumenintegral aussieht, das du beim Berechnen eines Trägheitsmomentes bekommst, hängt von den Koordinaten ab, die du in der Berechnung verwendest.
Das Trägheitsmoment für einen Körper mit homogener Dichte 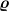 ist: ist:

Dabei ist r der Abstand des jeweiligen Volumenelementes dV von der Rotationsachse.
Für einen Quader mit den Seitenlängen a, b und c kann man in kartesischen Koordinaten x, y und z rechnen. Da ist das Volumenelement

und wenn die Drehachse durch den Mittelpunkt des Quaders geht und in z-Richtung zeigt, dann ist

Für das Trägheitsmoment erhält man also folgendes Dreifachintegral:
 \, \dd x \, \dd y \, \dd z )
Wie du siehst, stehen hier bei dieser Berechnung in kartesischen Koordinaten gar keine zusätzlichen Faktoren von  und keine Faktoren von und keine Faktoren von 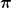 mit im Integral. mit im Integral.
--------------------------------------------------------
Faktoren von 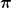 oder zusätzliche Faktoren von r bekommt man nur dann in dem Integral, wenn man das Trägheitsmoment für runde Körper ausrechnen möchte und dafür zum Beispiel Zylinderkoordinaten verwendet. Dann muss man also dementsprechend das Volumenelement in Zylinderkoordinaten verwenden. oder zusätzliche Faktoren von r bekommt man nur dann in dem Integral, wenn man das Trägheitsmoment für runde Körper ausrechnen möchte und dafür zum Beispiel Zylinderkoordinaten verwendet. Dann muss man also dementsprechend das Volumenelement in Zylinderkoordinaten verwenden. |
eine frage dazu wieso fängst du mit dem z integral an und nicht mit dem x integral also bei dir steht dx dy dz aber die integrale stehen von links nach rechts z y x
außerdem wie funktioniert das bei nicht konstantem rho ???
muss ich einfach die funktion mit einbeziehen? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. Dez 2006 23:40 Titel: dermarkus Verfasst am: 07. Dez 2006 23:40 Titel: |
 |
|
Wenn man so ein Mehrfachintegral ausrechnet, dann rechnet man das innerste Integral zuerst aus (hier also das über x), dann das über y, und dann das Integral über z. Daher die Reihenfolge von innen nach außen.
Wenn die Dichte nicht überall konstant ist, dann muss man die Dichte als Funktion, die von x, y und z abhängt, einsetzen:
 \varrho(x,y,z) \, \dd x \, \dd y \, \dd z )
Das kann man dann also erst integrieren, wenn man konkret einsetzen kann, wie das rho aussieht. |
|
 |
Diger_Diga
Anmeldungsdatum: 12.08.2006
Beiträge: 15
|
 Diger_Diga Verfasst am: 07. Dez 2006 23:51 Titel: Diger_Diga Verfasst am: 07. Dez 2006 23:51 Titel: |
 |
|
würde es nicht viel mehr sinn machen von links nach rechts zu integrieren und links x in der mitte y und rechts z zu schreiben auf der rechten seite steht ja auch erst dx dy dz!!!
angenommen die dichtefunktion ist abhängig nur vom radius r kommt dann noch ne variable dazu oder schreib ich dann dass rho abhängig ist von x und y nur weil z is ja net abhängig! demnach würde da ja so aussehen
r=sqrt(x^2+y^2)
also rho(r) = 10 - 0.0001*r^2 = 10 - 0.0001*(x^2+y^2)
was passiert wenn die funktion rho(r) = rho (x,y) = 10 - 0.0001*r = 10 - 0.0001*sqrt(x^2+y^2) also dann hab ich ja ganz böse wurzeln zum aufleiten? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 08. Dez 2006 00:06 Titel: dermarkus Verfasst am: 08. Dez 2006 00:06 Titel: |
 |
|
Integrale musst du von innen nach außen ordnen, sonst macht die Schreibweise keinen Sinn. Die Variable, über die das Integral läuft, muss sowohl vorne beim Integral als auch hinten beim zugehörigen "d..." stehen.
 \varrho(x,y,z) \, \dd x \right) \, \dd y \, \dd z )
Schau dir mal die große Klammer im Integral an: Das ist das Integral über x ... dx. Das berechnet man zuerst.
----------
(Und falls du nun meinst: "Wäre es nicht auch eine Möglichkeit, dasselbe zu meinen, es aber anders geordnet zu schreiben", dann lautet die Antwort: Das schreibt man nicht so, man hat sich in der Mathematik darauf geeinigt, die Variablen von innen nach außen zu ordnen.)
-------------
Wenn die Dichte von r abhängt und du kartesische Koordinaten verwendest, um das Integral auszurechnen, dann musst du erst das r in kartesische Koordinaten umwandeln, bevor du anfängst, das Integral zu berechnen. Wenn dabei Terme entstehen, die schwierig zu integrieren sind, dann ist das eben so 
Wenn die Terme so kompliziert werden, dass das Integrieren sehr schwierig wird, dann kann man versuchen, zum Beispiel das ganze in Zylinderkoordinaten zu rechnen, und hoffen, dass es da besser geht.
------------
Aber ich glaube, bevor wir da allgemein drüber reden, wie das in welchem Fall funktioniert, ist es besser, man versucht sich an einem konkreten Problem, wenn man das als Aufgabe gestellt bekommt. |
|
 |
Diger_Diga
Anmeldungsdatum: 12.08.2006
Beiträge: 15
|
 Diger_Diga Verfasst am: 08. Dez 2006 00:17 Titel: Diger_Diga Verfasst am: 08. Dez 2006 00:17 Titel: |
 |
|
also so wie ich das da "vorgemacht habe" mit den koordinaten?
in zylinderkoordinaten ist es ja per summe einfach zu rechnen das hab ich ja hier schon reingestellt worauf aber keine antwort kam naja...
wie geht das per zylinderschreibweise über integrale?
anhand eines kreises kann ich ja schreiben:
 \, dr)
hab mal wieder irgendwelche fehler gemacht woran liegt der layout fehler diesma?
[Der Latex-Editor mag es nicht, wenn man innerhalb von Formeln die Enter-Taste drückt, ich habe die Zeilenumbrüche in der Formel mal rausgemacht, Gruß, dermarkus] |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 08. Dez 2006 00:26 Titel: dermarkus Verfasst am: 08. Dez 2006 00:26 Titel: |
 |
|
Das, was du da als Integral "anhand eines Kreises" hinschreibst, kann ich nicht nachvollziehen. Für was für einen Körper soll das das Trägheitsmoment sein? Um welche Achse soll sich dieser Körper drehen?
---------------------------------------------------
In Zylinderkoordinaten  , ,  und und 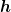 ist das Volumenelement ist das Volumenelement

Das kann man sich mit den Gleichungen für die Umrechnung zwischen den kartesischen Koordinaten und den Zylinderkoordinaten herleiten, siehe z.B. auch:
http://de.wikipedia.org/wiki/Polarkoordinaten |
|
 |
Diger_Diga
Anmeldungsdatum: 12.08.2006
Beiträge: 15
|
 Diger_Diga Verfasst am: 08. Dez 2006 00:33 Titel: Diger_Diga Verfasst am: 08. Dez 2006 00:33 Titel: |
 |
|
na super ich hasse diese verweise auf wikipedia da schlag ich immer sofort nach aber check das nicht diese erklärungsweise ist unnötig kompliziert obwohls auch einfacher geht... war bis jetzt ja immer so
das was da steht ist eine kugel die rotiert! |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 08. Dez 2006 00:50 Titel: dermarkus Verfasst am: 08. Dez 2006 00:50 Titel: |
 |
|
Das Integral, das du da hingeschrieben hast, ist für mich nicht das Trägheitsmoment einer Kugel, sondern die Masse einer Kugel.
(Kann es sein, dass du hier nicht zwischen dem Radius R der Kugel und dem Abstand r eines Volumenelementes von der Drehachse unterschieden hast, und dass du vergessen hast, das Volumenelement deiner nicht-kartesischen Koordinaten (denn du integrierst ja über r und nicht über x, y und z) richtig auszurechnen?)
Um das Trägheitsmoment einer Kugel zu berechnen, nimmt man am einfachsten Kugelkoordinaten. Wie das geht, ist sehr schön in Wikipedia vorgerechnet:
http://de.wikipedia.org/wiki/Tr%C3%A4gheitsmoment#Beispielrechnung:_Tr.C3.A4gheitsmoment_der_homogenen_Vollkugel
(Wenn du das für dich selbst lieber ausführlicher rechnen möchtest, oder wenn du erst noch zum Beispiel vorher ein paar Mathe-Grundlagen dazu lernen möchtest, um das gut nachvollziehen zu können, dann ist das okay. Denn diese Rechnung in Wikipedia ist für Leute gedacht, die schon die Mathe-Grundlagen dazu können.) |
|
 |
Diger_Diga
Anmeldungsdatum: 12.08.2006
Beiträge: 15
|
 Diger_Diga Verfasst am: 08. Dez 2006 00:58 Titel: Diger_Diga Verfasst am: 08. Dez 2006 00:58 Titel: |
 |
|
sorry hab das r^2 vergessen nochmal:
 \, dr)
oda nicht? |
|
 |
Diger_Diga
Anmeldungsdatum: 12.08.2006
Beiträge: 15
|
 Diger_Diga Verfasst am: 08. Dez 2006 01:06 Titel: Diger_Diga Verfasst am: 08. Dez 2006 01:06 Titel: |
 |
|
eigentlich heißt es ja:
 was ich aber auch schreiben kann als was ich aber auch schreiben kann als  und kann ich dieses dV nicht umschreiben in dr wieder bzw. das müste doch irgendwie gehen und kann ich dieses dV nicht umschreiben in dr wieder bzw. das müste doch irgendwie gehen
das volumen der kugel ist doch auch = \int^{r}_{0} dV(kugel) = \int^{r}_{0} 4*\pi*r^2 \, dr) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 08. Dez 2006 02:02 Titel: dermarkus Verfasst am: 08. Dez 2006 02:02 Titel: |
 |
|
| Diger_Diga hat Folgendes geschrieben: |
 was ich aber auch schreiben kann als was ich aber auch schreiben kann als  und kann ich dieses dV nicht umschreiben in dr wieder bzw. das müste doch irgendwie gehen und kann ich dieses dV nicht umschreiben in dr wieder bzw. das müste doch irgendwie gehen
|
Damit bin ich fast einverstanden: Es heißt:
 und damit und damit 
wenn du mit r den Abstand des jeweiligen Volumenelements von der Drehachse bezeichnen möchtest.
Mit  ist dabei das Volumenintegral über die gesamte Kugel gemeint, ohne dass man bisher dazusagt, in welchen Koordinaten man das gleich rechnen möchte. ist dabei das Volumenintegral über die gesamte Kugel gemeint, ohne dass man bisher dazusagt, in welchen Koordinaten man das gleich rechnen möchte.
Wenn du dich jetzt entscheidest, in welchen Koordinaten du das Volumenintegral ausrechnen möchtest, dann wird das eine Volumenintegral vorne zu drei verschiedenen Integralen über die drei Koordinaten deines Koordinatensystems, und das Volumenelement dV hinten wird zu dem Volumenelement in den entsprechenden Koordinaten.
Hier wird man am besten Kugelkoordinaten wählen, also  , , 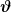 und und  . Dann ist das Volumenelement . Dann ist das Volumenelement

Und weil das r in Kugelkoordinaten den Abstand zum Kugelmittelpunkt meint, muss man nun für den Abstand zur Drehachse etwas anderes schreiben (sonst verwendet man denselben Buchstaben für zwei ganz unterschiedliche Sachen und bringt sie beim Rechnen durcheinander), nämlich  , wenn die Drehachse in Richtung der z-Achse zeigen soll. , wenn die Drehachse in Richtung der z-Achse zeigen soll.
Das musst du noch mit Hilfe von

und

in Kugelkoordinaten ausdrücken, und dann bekommst du das Dreifachintegral

zum Ausrechnen.
-----------------
Diesen bisherigen und auch den weiteren Teil der Rechnung findest du auch in der Wikipedia-Rechnung im Link oben. |
|
 |
Diger_Diga
Anmeldungsdatum: 12.08.2006
Beiträge: 15
|
 Diger_Diga Verfasst am: 08. Dez 2006 12:09 Titel: Diger_Diga Verfasst am: 08. Dez 2006 12:09 Titel: |
 |
|
ich glaube meine probleme liegen bei den buchstaben!
was sind das für komische zeichen und was geben die an
phi soll einen winkel angeben?was ist das komische kringelige v für ein zeichen sowas habe ich noch nie gesehn
und was sind kugelkoordinaten???
die formel r* sin* sin
und r * sin * sin bereitet mir auch schwierigekeiten welche winkel sind gemeint? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
|
 |
Diger_Diga
Anmeldungsdatum: 12.08.2006
Beiträge: 15
|
 Diger_Diga Verfasst am: 08. Dez 2006 17:17 Titel: Diger_Diga Verfasst am: 08. Dez 2006 17:17 Titel: |
 |
|
ich versteh nicht warum die da schreiben der winkel 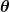 ist ist ) für mich ist für mich ist )
außerdem ist ) für mich jedenfalls für mich jedenfalls
das macht aber wieder sinn: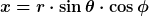

 |
|
 |
Diger_Diga
Anmeldungsdatum: 12.08.2006
Beiträge: 15
|
 Diger_Diga Verfasst am: 08. Dez 2006 19:37 Titel: Diger_Diga Verfasst am: 08. Dez 2006 19:37 Titel: |
 |
|
| dermarkus hat Folgendes geschrieben: |
Hier wird man am besten Kugelkoordinaten wählen, also  , , 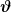 und und  . Dann ist das Volumenelement . Dann ist das Volumenelement

|
versteh nicht ganz wo ist denn der cos theta cos phi und sin phi abgeblieben? |
|
 |
Diger_Diga
Anmeldungsdatum: 12.08.2006
Beiträge: 15
|
 Diger_Diga Verfasst am: 09. Dez 2006 18:25 Titel: Diger_Diga Verfasst am: 09. Dez 2006 18:25 Titel: |
 |
|
hallo ???? ich versteh nicht so ganz wie diese formel zustande kommt!
wenn die x y z werte ganz anders aussehen! |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 11. Dez 2006 01:46 Titel: dermarkus Verfasst am: 11. Dez 2006 01:46 Titel: |
 |
|
| Diger_Diga hat Folgendes geschrieben: | ich versteh nicht warum die da schreiben der winkel 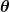 ist ist ) für mich ist für mich ist ) |
Das ist dasselbe, wenn du dich daran erinnerst, dass der cot gerade der Kehrwert des tan ist.
| Diger_Diga hat Folgendes geschrieben: |
das macht aber wieder sinn: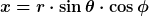

 |
Magst du damit mal
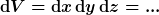
ausrechnen, indem du die drei Gleichungen für x, y und z verwendest und dann mit dem, was du über sin und cos weißt, das ergebnis für das Volumenelement so weit wie möglich vereinfachst? |
|
 |
Diger_Diga
Anmeldungsdatum: 12.08.2006
Beiträge: 15
|
 Diger_Diga Verfasst am: 11. Dez 2006 12:45 Titel: Diger_Diga Verfasst am: 11. Dez 2006 12:45 Titel: |
 |
|
ich glaube um die frage klare auszudrücken!
ich weiß nicht genau wie man über die 3 formel auf die integral schreibweise kommt. das ist mir schleierhaft!
bei 4/3 * pi * r^3 ist das ja noch zu sehen dass 4*pi*r^2 integriert das volumen ergibt aber dabei? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 11. Dez 2006 15:18 Titel: dermarkus Verfasst am: 11. Dez 2006 15:18 Titel: |
 |
|
Hast du in deiner Vorlesung über höhere Mathematik schon die Jacobi-Matrix gelernt? Mit der lässt sich am übersichtlichsten schreiben, wie du die Differentiale 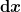 , ,  und und 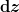 in die Differential in die Differential  , ,  und und  umrechnen kannst. umrechnen kannst.
Für diese Umrechnung muss man die Produktregel fürs Ableiten verwenden, die Jacobi-Matrix ist eine elegante Schreibweise, um das ganze übersichtlich darzustellen:
 = J \left ( \begin{matrix} \dd r \\ \dd \vartheta \\ \dd \varphi \end{matrix} \right ) )
mit der Jacobi-Determinante für die Koordinatentransformation von Kugelkoordinaten zu kartesichen Koordinaten wie in
http://de.wikipedia.org/wiki/Kugelkoordinaten#Jacobi-Matrix
Ich möchte hier wirklich nicht anfangen, komplette Kapitel aus Büchern über Höhere Mathematik oder komplette Seiten aus dem Internet abzuschreiben, oder hier im Physikerboard anfangen, zu versuchen, Mathematikvorlesungen zu halten.
Schaffst du es mit den bisherigen Tipps schon, die entsprechenden Kapitel in Büchern oder die Wikipedia-Links, die ich dir gegeben habe, durchzuarbeiten und nachzuvollziehen? Kannst du dir die eventuell noch fehlenden mathematischen Grundlagen, die du dafür noch brauchst, selbst aneignen?
Falls du das noch nicht so einfach schaffst, dann würde ich vorschlagen, entweder, falls du noch warten magst, zu bis zu deinem Studium und einer höheren-Mathematik-Vorlesung zu warten, in der du das dann lernst, oder, falls du dir das jetzt gleich erarbeiten magst, dich mit meinen Tipps und einem guten Mathebuch oder mit guten Internetseiten hinzusetzen, das durchzuarbeiten, nachzuvollziehen und nachzurechnen und wenn du dabei merkst, dass du noch Fragen hast und noch Hilfe beim Erarbeiten der mathematischen Grundlagen brauchen kannst, dann sind diese Fragen vielleicht noch besser nebenan im Matheboard aufgehoben. |
|
 |
Gimel

Anmeldungsdatum: 06.11.2007
Beiträge: 96
Wohnort: Wuppertal
|
 Gimel Verfasst am: 12. Dez 2007 00:04 Titel: Gimel Verfasst am: 12. Dez 2007 00:04 Titel: |
 |
|
Hmmm, habe mir jetzt so durchgelesen was hier steht und bin dann selber losgegangen das Trägheitsmoment eines quaders zu berechnen. Allerdings ist mein ergebniss von dem was die literatur angibt ( genau genommen um 1/4 ). Könntet ihr mir vielleicht sagen wo mein Fehler liegt:
Zunächst habe ich folgendes stehen:
~da~db~dc)
Das rho habe ich ausgeklammert, weil die Dichte in diesem fall konstant sein soll.
Aber nach dem Integrieren erhalte ich:
 = \frac{1}{3} *M * (a^2 + b^2))
Wo ist denn mein Fehler? habe ich mich beim Integrieren vertan oder war doch etwas am ansatz falsch? Kann es sein, dass ich das rho nicht ausklammern darf obwohl es konstant ist? |
|
 |
magneto42
Anmeldungsdatum: 24.06.2007
Beiträge: 854
|
 magneto42 Verfasst am: 12. Dez 2007 01:18 Titel: magneto42 Verfasst am: 12. Dez 2007 01:18 Titel: |
 |
|
Hallo Gimel.
Der Ansatz ist im Prinzip richtig. Bist Du sicher, daß Du die Grenzen wirklich richtig eingesetzt hast? Hast Du die dritte Potenz von  bzw. bzw.  richtig berechnet? richtig berechnet?
PS:
Ich rate dazu im Integranden nicht a, b und c zu verwenden, sondern die kartesischen Koordinaten x, y und z. Damit vermeidet man Verwirrung bezüglich der Grenzen. |
|
 |
Gimel

Anmeldungsdatum: 06.11.2007
Beiträge: 96
Wohnort: Wuppertal
|
 Gimel Verfasst am: 12. Dez 2007 16:58 Titel: Gimel Verfasst am: 12. Dez 2007 16:58 Titel: |
 |
|
hmm hat sich erledigt, habe tatsächlich die grenzen einfach nur falsch eingesetzt...
danke  |
|
 |
|




















 .
.

 .
.

 Alleine bekomme ich das sicher nie hin
Alleine bekomme ich das sicher nie hin 

