| Autor |
Nachricht |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 25. Jan 2016 20:30 Titel: GvC Verfasst am: 25. Jan 2016 20:30 Titel: |
 |
|
| Random hat Folgendes geschrieben: | | r ist doch immer der Abstand vom äußeren Punkt des drehenden Körpers zur Drechachse. Beim Ring links im Bild ist dass einfach r2. |
Nein. In der Formel für das Trägheitsmoment ist r der Abstand des jeweiligen infinitesimal kleinen Masseteilchens dm von der Drehachse. Anderenfalls wäre die Integration trivial.
| Random hat Folgendes geschrieben: | | Und für das Bild rechts, kann man den Satz von Steiners anwenden: |
Im Prinzip ja. Aber nicht so wie Du es vorhast. Du musst das Trägheitsmoment des Lochbereiches inklusive Steiner-Anteil berechnen, als ob es dieselbe Dichte wie das übbrige Rad habe. Dieses Trägheitsmoment musst Du dann von dem des Rades (ohne Loch) subtrahieren.
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 25. Jan 2016 23:06 Titel: Random Verfasst am: 25. Jan 2016 23:06 Titel: |
 |
|
Ah okay danke.
Also dann so:
)
Hm, dann verstehe ich aber den Satz von Steiner nicht, den ich oben so hingeschrieben habe, denn da wird ja nichts subtrahiert, ich wollts halt 1:1 so anwenden.
Verständnisproblem: Mir ist irgendwie nicht recht klar, warum bei der Scheibe mit Loch die Rotationsachse genau beim Loch sein soll. Kannst du mir das näher erklären bitte?
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 25. Jan 2016 23:37 Titel: GvC Verfasst am: 25. Jan 2016 23:37 Titel: |
 |
|
| Random hat Folgendes geschrieben: | | Hm, dann verstehe ich aber den Satz von Steiner nicht, den ich oben so hingeschrieben habe, denn da wird ja nichts subtrahiert, ... |
Was Du hingeschrieben hast, war ja auch falsch. Da gab es nichts zu verstehen.
| Random hat Folgendes geschrieben: | | Verständnisproblem: Mir ist irgendwie nicht recht klar, warum bei der Scheibe mit Loch die Rotationsachse genau beim Loch sein soll. |
e ist doch der Abstand zwischen Mittelpunkt der großen Scheibe und Mittelpunkt des Loches, oder nicht? Also geht die Rotationsachse nach wie vor durch den Mittelpunkt der großen Scheibe.
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 27. Jan 2016 00:01 Titel: Random Verfasst am: 27. Jan 2016 00:01 Titel: |
 |
|
Dann verstehe ich denn Satz nocht nicht.
Ist die Rotationsachse dann immer in der Mitte eines Objektes egal wie es verformt ist, oder wieviele Löcher es hat?
Ich dachte den Satz von Steiners kann man anwenden, wenn die Rotationsachse paralell verschoben wird.
Ich hab mir verschiedene Artikel im Internet durchgelesen und verstehe noch immer nicht, was jetzt genau damit gemeint ist.
Kannst du mir da weiterhelfen bitte?
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 27. Jan 2016 01:25 Titel: GvC Verfasst am: 27. Jan 2016 01:25 Titel: |
 |
|
| Random hat Folgendes geschrieben: | | Ist die Rotationsachse dann immer in der Mitte eines Objektes egal wie es verformt ist, oder wieviele Löcher es hat? |
Die Rotationsachse ist in der Aufgabenstellung vorgegeben, nämlich als die Achse durch den Mittelpunkt der großen Scheibe. Lies Dir den letzten Satz der Aufgabenstellung durch. Da steht das eindeutig drin.
| Random hat Folgendes geschrieben: | | Ich dachte den Satz von Steiners kann man anwenden, wenn die Rotationsachse paralell verschoben wird. |
So ist es.
Das Trägheitsmoment der kleinen Scheibe, welches Du

genannt hast, ist das bzgl. der Drehachse durch den Mittelpunkt des Loches. Die tatsächliche Rotationsachse ist gegenüber dieser Drehachse um e verschoben. Also kommt zum Trägheitsmoment des "Loches" noch der Steiner-Anteil dazu.

|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 27. Jan 2016 23:08 Titel: Random Verfasst am: 27. Jan 2016 23:08 Titel: |
 |
|
Ok, danke. Es wird besser.
D.h. man hat immer die Rotationsachse des Körpers gegeben, wie in dem Fall ist es halt der Mittelpunkt des Rades. Und wenn ich dann ein Loch irgendwo drinnen habe und ich den Abstand zwischen der realen Rotationachse und der Rotationsachse oder halt Schwerpunkt des Loches kenne und diese dann auch ncoh parallel zueinander sind, kann ich mir mir das Trägheitsmoment des Loches bzgl. der "realen Rotationsachse" mit Hilfe Satz von Steiner berechnen und dann muss ich das vom Trägheitsmoment der vollen Scheibe abziehen und ich habe mein Trähgheitsmoment des Körpers.
Richtig?
Im Anhang befindet sich noch ein Bespiel.
Die reale Rotationsachse ist hier immer am Ende des Stabes, sieht man auch schön eingezeichnet.
Naja hier rotiert das ganze ja nicht um die Schwerpunktachse des Stabes. Also der Abstand zur Schwerpunktachse und realen Rotationsachse ist ja l/2 bei (a).
Aber da ist es anders, denn ich hab ja kein "Gesamtpaket" hier, wie die Volle Scheibe beim anderen Beispiel. Hast du vielleicht einen Tipp für mich, so kann ich es dann versuchen zu lösen und verstehs dann bestimmt besser.
| Beschreibung: |
|

Download |
| Dateiname: |
homogener_stab.png |
| Dateigröße: |
36.61 KB |
| Heruntergeladen: |
714 mal |
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 29. Jan 2016 19:39 Titel: franz Verfasst am: 29. Jan 2016 19:39 Titel: |
 |
|
Randbemerkung
Das (axiale) Trägheitsmoment hat erstmal nichts mit einer möglichen Symmetrieachse des Körpers zu tun oder mit seiner tatsächlichen Rotationsachse, sondern es wird ganz formal bezüglich einer willkürlichen Geraden berechnet. Das könnte bei einem Stab beispielsweise senkrecht zur Mitte oder zu einem Ende sein, oder auch zur Längsachse.
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 30. Jan 2016 15:44 Titel: Random Verfasst am: 30. Jan 2016 15:44 Titel: |
 |
|
Kann mir wer weiterhelfen mit meinem letzten Beitrag hier bitte? Ich glaube ich hab den Satz noch nicht so ganz verstanden.
@franz Naja man kann es schon zu irgendeiner Geraden berechnen, aber das berechnete Trägheitsmoment gilt halt nur, wenn das Objekt gerade um diese Gerade rotiert, oder?
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 30. Jan 2016 16:16 Titel: Duncan Verfasst am: 30. Jan 2016 16:16 Titel: |
 |
|
| Random hat Folgendes geschrieben: |
@franz Naja man kann es schon zu irgendeiner Geraden berechnen, aber das berechnete Trägheitsmoment gilt halt nur, wenn das Objekt gerade um diese Gerade rotiert, oder? |
Nein. Das Trägheitsmoment hängt nicht davon ab, ob der Körper rotiert oder nicht rotiert.
Du erhälst eher Antworten, wenn du nur eine Aufgabe pro Thread stellst.
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 30. Jan 2016 18:21 Titel: Random Verfasst am: 30. Jan 2016 18:21 Titel: |
 |
|
Ja, aber die Aufgaben hängen ja zusammen. Ich will nur den Satz von Steiner verstehen und wenn ich da parallel das versuche, dann ist das blöd.
Und ja, es ist egal ob sich der Körper dreht oder nicht dreht, aber man nimmt doch als Bezugspunkt irgend eine Gerade und das Trägheitsmoment gilt dann auch wenn ich den Körper um die Rotationsachse in der Mitte rotatieren lasse?
Ich glaube nicht, denn das wäre unlogisch.
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 30. Jan 2016 18:36 Titel: Duncan Verfasst am: 30. Jan 2016 18:36 Titel: |
 |
|
| Random hat Folgendes geschrieben: |
Und ja, es ist egal ob sich der Körper dreht oder nicht dreht, aber man nimmt doch als Bezugspunkt irgend eine Gerade und das Trägheitsmoment gilt dann auch wenn ich den Körper um die Rotationsachse in der Mitte rotatieren lasse?
Ich glaube nicht, denn das wäre unlogisch. |
Was genau findest du unlogisch?
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 30. Jan 2016 19:19 Titel: Random Verfasst am: 30. Jan 2016 19:19 Titel: |
 |
|
Ja das Trägheitsmoment ist doch so definiert:

Okay, ich wollte gerade eine Erklärung dafür schreiben, dass r der Abstand immer zur Masse dm ist, aber das ergibt keinen Sinn.
Auf jedenfall ist dm ein unendlich kleines Massenstück vom Körper und ich dachte halt das r der Abstand von der Rotationsachse zu diesem Massenstück immer ist, aber das kann nicht sein, da ja r in dem Fall konstant ist, also laut Formel.
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 30. Jan 2016 19:26 Titel: franz Verfasst am: 30. Jan 2016 19:26 Titel: |
 |
|
|
r ist der senkrechte Abstand (das Lot) von dem Massestück dm zu der vorher festgelegten Geraden ("Achse").
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 30. Jan 2016 19:32 Titel: Duncan Verfasst am: 30. Jan 2016 19:32 Titel: |
 |
|
Jetzt weiß ich aber noch immer nicht, was du als unlogisch angesehen hast.
Jetzt schreibst du, dass eine Erklärung, dass r immer der Abstand zur Masse dm sei, keinen Sinn ergibt.
Außerdem schreibst du, dass r ja in dem Fall konstant sei, laut der Formel.
In was für einem Fall?
Laut welcher Formel?
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 30. Jan 2016 19:37 Titel: Random Verfasst am: 30. Jan 2016 19:37 Titel: |
 |
|
Also die Formel hier:
Und r ist der Abstand von der Rotationsachse zur unendlich kleinen Masse dm des jeweiligen Körpers. Also der Körper hat ja unendlich viele kleine Massen und die summiert man halt per Integral und jede Masse dm hat einen anderen Abstand zu der Rotationsachse, richtig?
Also so verstehe ich das.
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 30. Jan 2016 19:40 Titel: Duncan Verfasst am: 30. Jan 2016 19:40 Titel: |
 |
|
Das ist richtig.
Aber wie kommst du auf die Idee, dass r konstant sei?.
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 30. Jan 2016 20:51 Titel: Random Verfasst am: 30. Jan 2016 20:51 Titel: |
 |
|
r ist eh nicht konstant, ich habe mich da vertan. Sorry für den Doppelpost, aber irgendwie geht das Forum immer offline und ich weiß nie, ob der Beitrag dann gepostet wurde. [as_string: Ich hab mal die Doppelposts gelöscht. Wenn Du schon gemerkt hast, dass es öfter zu Doppelposts kommt, warum wartet man dann nicht erst und schaut kurz, ob es vielleicht doch angenommen wurde, bevor man dann nochmal postet? Wir haben halt zur Zeit die Probleme mit den DDoS Angriffen...]
(Erstmal ohne Satz von Steiner)
Schauen wir uns vielleicht mal bitte das Beispiel an zum homogenen Stab, aber Teil b erstmal(das zweite Bild, dass ich gepostet habe vor ein paar Beiträgen).
Hier muss ich also dm ausdrücken, sodass ich gut integrieren kann. Naja wir sehen ja die Rotationsachse ganz rechts und der Abstand von diese Rotationsachse zu den jeweiligen Massestücken dm ist dann unser r.
Also müssen wir jetzt dm und r irgendwie ausdrücken. dm kann man gut
durch die Dicht ausdrücken.
 wobei m die Gesamtmasse und L die Gesamtlänge des Stabe ist. Und dann gilt auch wobei m die Gesamtmasse und L die Gesamtlänge des Stabe ist. Und dann gilt auch  , also die ganz kleine Masse muss doch auch glech der Dichte multipliziert mit der ganz kleinen Länge dieser Masse. , also die ganz kleine Masse muss doch auch glech der Dichte multipliziert mit der ganz kleinen Länge dieser Masse.
x soll der Abstand von ganz oben des Stabes bis zum Massestück sein, dann können wir ) schreiben. schreiben.
Und das kann ich dann in die besagte "Formel" einsetzen, jedoch würde dann da stehen:
)^2 \rho dl) Aber eigentlich müsste ich ja über x integrieren, weil sich der Abstand immer änder muss, aber darf ich statt dl einfach dx schreiben? Das muss doch mit der Dichte und so stimmen, oder nicht? Aber eigentlich müsste ich ja über x integrieren, weil sich der Abstand immer änder muss, aber darf ich statt dl einfach dx schreiben? Das muss doch mit der Dichte und so stimmen, oder nicht?
Das verstehe ich z.B. nicht.
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 30. Jan 2016 21:20 Titel: franz Verfasst am: 30. Jan 2016 21:20 Titel: |
 |
|
Es wird über den gesamten Körper integriert, also  ^2 \ \lambda\ dx}) . .
Statt 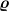 schreibe ich für die Längendichte lieber was andres schreibe ich für die Längendichte lieber was andres  . .
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 30. Jan 2016 21:29 Titel: Random Verfasst am: 30. Jan 2016 21:29 Titel: |
 |
|
Danke, dass von 0 bis L integriert wird ist klar, nur ist das  oder nicht? Und wenn ich das in die "Formel" einsetzen steht da ja dl und nicht dx, aber das ist doch nicht dasselbe oder? oder nicht? Und wenn ich das in die "Formel" einsetzen steht da ja dl und nicht dx, aber das ist doch nicht dasselbe oder?
Und das ist mein Problem hier, was ich nicht verstehe.
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 30. Jan 2016 21:41 Titel: franz Verfasst am: 30. Jan 2016 21:41 Titel: |
 |
|
|
Ich empfehle x und dx. l und dl kann zu Verwechslungen bei der Gesamtlänge l führen (deshalb auch besser L). Geschmackssache.
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 30. Jan 2016 22:00 Titel: Random Verfasst am: 30. Jan 2016 22:00 Titel: |
 |
|
Ja aber ich dachte ich muss das dm in der "formel" irgendwie ausdrücken, oder nicht?
Wenn die Gesamtmasse M gleich der Dichte multipliziert mit der Gesamtlänge L ist, dann muss ja dM gleich die Dichte multipliziert mit der Länge des kleinen Masseteilchen dm sein. Und diese Länge ist doch L abgeleitet also dl.
Wie kann ich also dm durch dx ausdrücken?
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 31. Jan 2016 01:59 Titel: franz Verfasst am: 31. Jan 2016 01:59 Titel: |
 |
|

Die Bezeichnungen sind, wie schon gesagt, ziemlich egal - solange man weiß, was man tut. Ob M oder m, L oder  oder x ... oder x ...
Nur "Dichte" würde ich für  vermeiden. Bei einem angenommen Querschnitt A des Stabes ist vermeiden. Bei einem angenommen Querschnitt A des Stabes ist  . .
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 31. Jan 2016 11:27 Titel: Random Verfasst am: 31. Jan 2016 11:27 Titel: |
 |
|
Ja, ich verstehe worauf du hinaus willst.  ist ja sozusagen die "längendichte" und nicht die klassische dichte so wie man sie kennt. ist ja sozusagen die "längendichte" und nicht die klassische dichte so wie man sie kennt.
Ich verstehe dann nicht, wie man sagen kann  , wenn , wenn  . .
Wie kommst du von  auf auf  ? ?
M ist die Gesamtmasse und L die Gesamtlänge, wie schon erwähnt, und dann dm ein unendlich kleines Masseteilchen des Stabes und x der derzeitige Abstand zum Masseteilchen dm.
Und wenn ich mir die Formel  angucke und ich dann dm berechnen will, dann kann aus Gesamtlänge DER Gesamtmasse niemals ein dx werden, sondern sodass die Längendichteformel weiterhin stimmen würde, müsste man statt dx (was ja der kleinste Abstand zu dm ist) irgendetwas anderes schreiben, dass die Länge des Massteilchen repräsentiert. angucke und ich dann dm berechnen will, dann kann aus Gesamtlänge DER Gesamtmasse niemals ein dx werden, sondern sodass die Längendichteformel weiterhin stimmen würde, müsste man statt dx (was ja der kleinste Abstand zu dm ist) irgendetwas anderes schreiben, dass die Länge des Massteilchen repräsentiert.
Das verwirrt mich so, weißt du was ich meine?
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 31. Jan 2016 11:35 Titel: as_string Verfasst am: 31. Jan 2016 11:35 Titel: |
 |
|
| Random hat Folgendes geschrieben: | | M ist die Gesamtmasse und L die Gesamtlänge, wie schon erwähnt, und dann dm ein unendlich kleines Masseteilchen des Stabes und x der derzeitige Abstand zum Masseteilchen dm. |
Nein, Dein l entspricht seinem x. Weder x noch l ist der Abstand zwischen Rotationsachse und Masseelement, sondern diese Größe multipliziert mit dem Sinus des Öffnungswinkel. Das hat franz doch auch schon so geschrieben gehabt...
Gruß
Marco
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 31. Jan 2016 11:39 Titel: GvC Verfasst am: 31. Jan 2016 11:39 Titel: |
 |
|
Die längenbezogene Dichte ist

Dann hat ein infinitesimal kleiner Abschnitt mit der Länge dx die infinitesimal kleine Masse

|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 31. Jan 2016 11:46 Titel: as_string Verfasst am: 31. Jan 2016 11:46 Titel: |
 |
|
@GvC: Ich vermute, das ist gar nicht sein Problem. Er meint einfach die ganze Zeit, das x hätte etwas mit der "x-Koordinate" im Koordinatensystem zu tun und sei damit gleich dem Abstand von der Rotationsachse. Aber das ist eben nicht der Fall und das scheint er einfach nicht zu verstehen.
Ich weiß auch nicht, was man da noch schreiben soll...
Gruß
Marco
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 31. Jan 2016 11:49 Titel: as_string Verfasst am: 31. Jan 2016 11:49 Titel: |
 |
|
Ich hab gerade nochmal gelesen... Offenbar ist das doch nicht der Punkt, an dem er hängt.
@random: Worin siehst Du den Unterschied zwischen x und l bzw. zwischen dx und dl? Das ist haargenau das selbe Ding, nur mit einem anderen Namen (Buchstaben...).
Gruß
Marco
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 31. Jan 2016 13:58 Titel: Random Verfasst am: 31. Jan 2016 13:58 Titel: |
 |
|
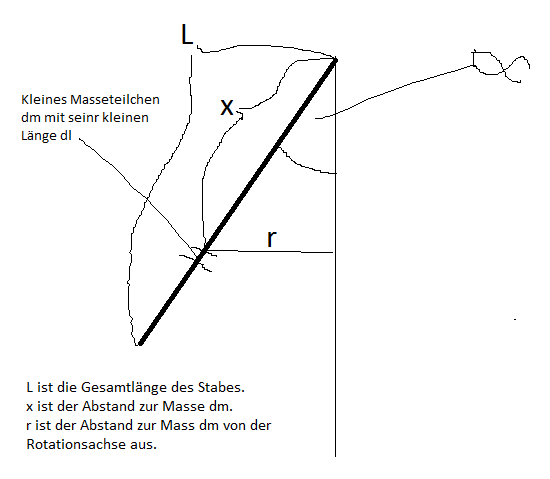
Okay, schaut euch bitte das Bild an.
Wie gesagt ist dann x) und und  . Wir suchen jetzt dm. Und unsere Längendichte . Wir suchen jetzt dm. Und unsere Längendichte  Also muss Also muss  sein. sein.
Und dann kann ich das r in das Integral einsetzen und auch für dm, jedoch steht dann ja dl da.
Ich finde mein Bild ist logisch, denn x ist genau der Abstand zur Masse dm, wie er eingezeichnet ist und hat nie irgendetwas mit der Länge von einer kleinen Masse zu tun. Da x ja den Abstand repräsentiert, so wie er eingezeichnet ist.
L hingegen ist die Gesamtlänge des Stabens, also ist auch x und L nicht dasselbe und nennen wir halt die Länge der ganz kleinen Masse(dm) einfach mal dl oder dy, dann hat das aber nichts mit x zu tun, so wie ich es eingezeichnet habe. Weiß nicht, was dx dann in meiner Zeichnung sein soll, eig. müsste dx dann ein sehr sehr kleiner Abstand sein.
| Beschreibung: |
|
| Dateigröße: |
11.58 KB |
| Angeschaut: |
24745 mal |
|
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 31. Jan 2016 14:12 Titel: GvC Verfasst am: 31. Jan 2016 14:12 Titel: |
 |
|
|
Warum setzt Du nicht einfach anstelle von dl das dx ein, denn Du zählst den Abstand der Masse dm vom Drehpunkt ja auch als x. Dann ist das, was Du dl nennst doch x+dx-x=dx oder etwa nicht. Du kannst natürlich, wie von franz bereits gesagt, den Abstand l nennen und die infinitesimal kleine Länge dl. Es könnte dann nur sein, dass Du das l (veränderlicher Abstand der infinitesimal kleinen Masse dm) mit L (feste Stablänge) verwechselst. Also mach, was Du willst, nur mach es richtig.
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 31. Jan 2016 15:20 Titel: Random Verfasst am: 31. Jan 2016 15:20 Titel: |
 |
|
Achso, also das dieses dl immer dieses kleine ding sein, dass man aufsummiert, also man fängt bei Null an und am Anfang ist der Stab 0cm Lang dann später 1cm lang etc. Ja und das ist dann dx!!
Endlich verstehe ich es, danke. Hatte den Megaknoten gerade. Danke!
Okay, nun möchte ich das mit dem Satz von Steiner lösen.
Angenommen wir haben einen Körper und wir wissen das Trägheitsmoment  bezüglich der Rotationsachse durch seinen Schwerpunkt. Jedoch haben wir jetzt die Rotationsachse parallel zu der Achse durch den SP und möchte nun das Trägheitsmoment bezüglich der Rotationsachse durch seinen Schwerpunkt. Jedoch haben wir jetzt die Rotationsachse parallel zu der Achse durch den SP und möchte nun das Trägheitsmoment  berechnen. berechnen.
Dann gilt:  wobei m die Masse des Körpers und e der Abstand von der Achse im SP zur parallel verschobenen Achse ist. wobei m die Masse des Körpers und e der Abstand von der Achse im SP zur parallel verschobenen Achse ist.
Wie würde man das in meinem Beispiel anwenden? Also beil Teil b ist es komisch, denn da ist es mit dem Satz genau so "schwer", denn man muss sich ja auch das Drehmoment durch den Schwerpunkt zuerst ausrechnen, aber der Stab ist halt hier "schief".
Bei teil a wärs einfacher. Also das Trägheitsmoment bzg. der Rotationsachse im Schwerpunkt wäre ja: 
Und dann: 
Richtig?
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 31. Jan 2016 22:55 Titel: GvC Verfasst am: 31. Jan 2016 22:55 Titel: |
 |
|
| Random hat Folgendes geschrieben: | | Achso, also das dieses dl immer dieses kleine ding sein, dass man aufsummiert, |
Nein, man summiert nicht dl auf und auch nicht dx. Die Vorschrift zur Bestimmung des Trägheitsmomentes ist eindeutig: Man summiert dm*r^2 auf, im vorliegenden Fall lambda*dx*x^2. Aber im Prinzip meinst Du das Richtige,
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 01. Feb 2016 00:13 Titel: Random Verfasst am: 01. Feb 2016 00:13 Titel: |
 |
|
Danke, dass meinte ich so, jetzt verteh ichs.
Stimmt das so oben mit dem Satz von Steiner?
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 01. Feb 2016 08:25 Titel: as_string Verfasst am: 01. Feb 2016 08:25 Titel: |
 |
|
Nein, da hast Du gleich mehrere Fehler eingebaut.
Der Schwerpunkt eines Stabs ist natürlich in seiner Mitte. Also musst Du nicht von 0 bis L integrieren, sondern von -L/2 bis +L/2
Wenn Du für e=L/2 einsetzt, dann musst Du natürlich das "/2" auch quadrieren, es steht also nicht L^2/2 sondern L^2/4 da.
Es gibt nur eine Masse. Warum Du mal ein kleines und mal ein großes M verwendest verstehe ich nicht.
Kontrollieren hättest Du Dich auch selbst schon gekonnt: Ob man vom Trägheitsmoment bezüglich des Schwerpunktes ausgeht und den Satz von Steiner verwendet oder das Trägheitsmoment direkt für die Achse ausrechnet, es sollte natürlich jeweils das selbe Ergebnis raus kommen.
Gruß
Marco
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 01. Feb 2016 09:12 Titel: franz Verfasst am: 01. Feb 2016 09:12 Titel: |
 |
|
OT
Moin Marco!
| as_string hat Folgendes geschrieben: | | Warum Du mal ein kleines und mal ein großes M verwendest verstehe ich nicht. |
Falls bin ich diese Schreibweise ausgelöst habe: Mir liegt an möglichst einfachen und angepaßten Bezeichnungen, wenig Indizes.
Wenn also hier mit einer Variablen Länge  bzw. bzw.  oder Masse oder Masse ) bzw. bzw. 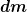 gearbeitet wird, so schreibe ich die konstanten Gesamtgrößen gern L oder M. Analog bei Dichte- oder Schwerebetrachtungen in einer Massekugel gearbeitet wird, so schreibe ich die konstanten Gesamtgrößen gern L oder M. Analog bei Dichte- oder Schwerebetrachtungen in einer Massekugel ,\ g(r)) und M, R. und M, R.
Geschmackssache halt. :-) mfG!
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 01. Feb 2016 10:20 Titel: Random Verfasst am: 01. Feb 2016 10:20 Titel: |
 |
|
Ok, danke Leute. Ich dachte, ob ich nun von 0 bis L gehe, oder von -L/2 bis L/2 ist egal. Und das mit der Masse ware in Tippfehler, sorry.
Jetzt zurück zum ganz ersten Beispiel mit Satz von Steiner bitte:
Wir haben die Rotationsachse im Mittelpunkt der Scheibe. Und parallel zum Abstand e könnte auch eine Achse sein, durch den Mittelpunkt des Loches.
Satz von Steiner:


1. Wenn J_1 mein Trägheitsmoment der ganzen Scheibe ohne Loch ist, dann ist J_2 das Trägheitsmoment, wenn die Rotationsachse im Mittelpunkt des Loches wäre, richtig?
2.
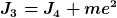

J_4 ist hier anscheined das Trägheitsmoment vom Loch. Also müsste J_3 das Trägheitsmoment sein, wenn außerhalb des Loches eine Rotationsachse ist. Aber hier betrachten wir ja nur das Loch als kleine Scheibe und die große Scheibe gibts ja nicht in dem Fall oder?
edit: warum wird latex nicht angezeigt?
|
|
 |
Duncan
Gast
|
 Duncan Verfasst am: 01. Feb 2016 10:59 Titel: Duncan Verfasst am: 01. Feb 2016 10:59 Titel: |
 |
|
Latex oder nicht Latex - hier herrscht Chaos!
Einmal ist von einem Stab die Rede, dann wieder von einem Loch usw.
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 01. Feb 2016 11:05 Titel: as_string Verfasst am: 01. Feb 2016 11:05 Titel: |
 |
|
Das fehlende Latex wird wohl auf die ständigen DDoS-Angriffe zurück zu führen sein. Thomas wird das hoffentlich auch wieder bald in den Griff bekommen können, vermutlich hat er aber noch ein paar andere Sorgen im Moment.
In diesem Thread werden wieder mehrere unterschiedliche Aufgaben behandelt, was ich für einen großen Schwachsinn halte und was nur zur Verwirrung aller und Missverständnissen führt. Ich hab schon öfter mal gemeckert, wenn das jemand macht, es aber mehr oder weniger inzwischen aufgegeben...
Gruß
Marco
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 01. Feb 2016 11:05 Titel: Random Verfasst am: 01. Feb 2016 11:05 Titel: |
 |
|
|
Okay, sorry. dann werde ich im Zukunft immer einen Thread pro Aufgabe erstellen. Sorry nochmals!
|
|
 |
|
















