| Autor |
Nachricht |
Orpheus
Anmeldungsdatum: 06.05.2007
Beiträge: 35
|
 Orpheus Verfasst am: 17. Jan 2010 15:34 Titel: Trägheitsmoment Kegel Orpheus Verfasst am: 17. Jan 2010 15:34 Titel: Trägheitsmoment Kegel |
 |
|
Hallo,
komme nicht ganz klar, bzw. habe Verständnisprobleme bei dem Ausrechnen des Trägheitsmoments eines Kegels:
Fange mal an: als allgemeine Formel zur Ausrechnung des Trägheitsmoment benutze ich:

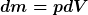 (p - Dichte) (p - Dichte)
und  (Kreis mit Höhe multipliziert und veränderlichem r = Kegel) (Kreis mit Höhe multipliziert und veränderlichem r = Kegel)
folgt:
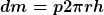
eingesetzt in 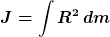

Wenn ich nun mit dem Kegelvolumen eliminiere, so dass m =p*v reinkommt, ergibt sich 3/8 R1²m Dabei sollen aber 3/10 herauskommen. Weiß jemand vlt. wo der Fehler liegt?
Irgendwie habe ich das Gefühl ich habe hier irgendetwas falsch verstanden. Habe nach einem Beispiel von Giancoli gerechnet.
Vielen vielen Dank für jegliche Hilfe. Grüße |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 17. Jan 2010 15:47 Titel: pressure Verfasst am: 17. Jan 2010 15:47 Titel: |
 |
|
Mit
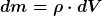
bin ich noch einverstanden.
Danach nicht mehr.Bei diesem Beispiel wäre es sinnvoll Zylinderkoordinaten zu nutzen.
Somit wäre 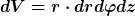 . .
Wenn du jetzt noch bei den Integrationsgrenzen die Abhängigkeit von z von r beachtest bzw. r von z, sollte nichts schief gehen. |
|
 |
Orpheus
Anmeldungsdatum: 06.05.2007
Beiträge: 35
|
 Orpheus Verfasst am: 17. Jan 2010 15:57 Titel: Orpheus Verfasst am: 17. Jan 2010 15:57 Titel: |
 |
|
Hallo,
stimmt, danke.
z ist doch konstant (Höhe), also muss ich doch nicht dz annehmen oder?
Dann würde folgen:

Wie integriere ich jetzt über 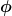 ? ?
Vielen Dank.
Grüße |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 17. Jan 2010 16:04 Titel: pressure Verfasst am: 17. Jan 2010 16:04 Titel: |
 |
|
Also erstmal ist z nicht konstant: z beschreibt ja die Höhe über den Radius r und die ist nicht konstant, sonst wäre es ja eine Zylinder und kein Kegel.
Deswegen sollst du dir mal Überlegen, wie dann die Funktion ) konkret aussieht. Nehmen wir mal an der Kegel steht nicht auf Spitze sondern auf der Bodenfläche. konkret aussieht. Nehmen wir mal an der Kegel steht nicht auf Spitze sondern auf der Bodenfläche.
Dein Integral sieht nun wie folgt aus:
}\! \rho \cdot r^3 \, dz \, dr \, d\varphi)
Da im Integranten kein  vorkommt kannst du es umschreiben zu: vorkommt kannst du es umschreiben zu:
}\! r^3 \, dz \, dr )
Etwas einfacher würde es wahrscheinlich gehen, wenn man den Kegel auf die Spitze stellt und dann r als Funktion von z betrachtet. Aber beides sollte das gleiche Ergebnis liefern.
Zuletzt bearbeitet von pressure am 18. Jan 2010 08:49, insgesamt 2-mal bearbeitet |
|
 |
Orpheus
Anmeldungsdatum: 06.05.2007
Beiträge: 35
|
 Orpheus Verfasst am: 17. Jan 2010 17:02 Titel: Orpheus Verfasst am: 17. Jan 2010 17:02 Titel: |
 |
|
Hallo, vielen Dank.
Wie komme ich den auf z(r)?
Ausgerechnet wäre das Volumenintegral dann ja:
 )
Danke.
Grüße |
|
 |
pressure
Anmeldungsdatum: 22.02.2007
Beiträge: 2496
|
 pressure Verfasst am: 17. Jan 2010 17:14 Titel: pressure Verfasst am: 17. Jan 2010 17:14 Titel: |
 |
|
Nein wäre es nicht, weil z eine Funktion von r ist und daher bei der Integration über r nicht als konstanter Faktor betrachtet werden kann. Auf diese Funktion kommst du indem du dir durch elementare Überlegungen herleitest, welche lokale Hohe ein Kegel beim Radius r hat. Wärst du mit folgender Funktion einverstanden:
 = h \cdot (1- \frac{r}{R})) |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 18. Jan 2010 10:22 Titel: VeryApe Verfasst am: 18. Jan 2010 10:22 Titel: |
 |
|
Ich versteh nicht, wieso sich die Leute die etwas berechnen wollen nicht ne kleine Skizze machen. Drehkegel zeichnen, wo ist die Drechachse und wie werden die einzelnen dI auf die Drehachse berechnet. dann können solche Missverständnisse wie z =konstant gar nicht auftreten. Man sieht gleich welche Punkte um die Drehachse die gleiche Geschwindigkeit haben.
Nur Punkte die in der Normalebene auf die Drehachse im gleichen Radius liegen |
|
 |
lena18
Anmeldungsdatum: 11.10.2009
Beiträge: 464
|
 lena18 Verfasst am: 18. Jan 2010 12:55 Titel: lena18 Verfasst am: 18. Jan 2010 12:55 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | | Ich versteh nicht, wieso sich die Leute die etwas berechnen wollen nicht ne kleine Skizze machen. dann können solche Missverständnisse wie z =konstant gar nicht auftreten. |
Ich bewundere alle Leute, die das trotzdem können, denn ich kanns leider nicht ... 
Stell dir mal vor du müsstest einen Schwerpunkt mit zig Teilflächen berechnen.
lena |
|
 |
El Rey
Anmeldungsdatum: 17.10.2010
Beiträge: 59
|
 El Rey Verfasst am: 07. Jan 2011 23:04 Titel: El Rey Verfasst am: 07. Jan 2011 23:04 Titel: |
 |
|
| pressure hat Folgendes geschrieben: | Nein wäre es nicht, weil z eine Funktion von r ist und daher bei der Integration über r nicht als konstanter Faktor betrachtet werden kann. Auf diese Funktion kommst du indem du dir durch elementare Überlegungen herleitest, welche lokale Hohe ein Kegel beim Radius r hat. Wärst du mit folgender Funktion einverstanden:
 = h \cdot (1- \frac{r}{R})) |
kannst du mir erklärn wie du auf die funktion kommst ich musste das jez auch mal berechnen und ich weis nich wie man auf die funktion kommt
wär mir echt ne große hilfe  |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 08. Jan 2011 02:05 Titel: franz Verfasst am: 08. Jan 2011 02:05 Titel: |
 |
|
Ohne irgendwas gelesen zu haben: Es "riecht" hier nach Kegel
 = h \cdot \left(1- \frac{r}{R}\right)\Rightarrow)
 = 0)
 = h) |
|
 |
Packo
Gast
|
 Packo Verfasst am: 08. Jan 2011 11:36 Titel: Packo Verfasst am: 08. Jan 2011 11:36 Titel: |
 |
|
Hallo Orpheus,
du brauchst dazu keine Zylinderkoordinaten.
Berechne zuerst das Massenträgheitsmoment einer Scheibe mit Radius R und Höhe H
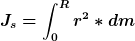
wobei
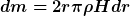
Als Ergebnis sllst du
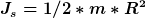
erhalten. m ist die Masse der Scheibe.
==========
Jetzt kommt der Kegel dran.
Höhe = H
Radius der Basis = R
Wir zerlegen den Kegel in Scheiben parallel zur Basis.
Eine solche Scheibe habe den Radius r und die Höhe dh.
also dJ = 1/2*r^2*dm
wir addieren (wir zählen die Koordinate h von der Spitze aus):
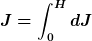
Eingesetzt und unter Berücksichtigung von r = R/H*h
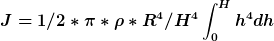
Weiters setzt du noch die Gesamtmasse des Kegels M ein
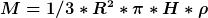
und du erhälst
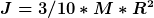
War doch nicht schwer - oder? |
|
 |
Loxeran
Anmeldungsdatum: 12.07.2012
Beiträge: 3
|
 Loxeran Verfasst am: 12. Jul 2012 19:00 Titel: Loxeran Verfasst am: 12. Jul 2012 19:00 Titel: |
 |
|
Hey ho Leute.
Also ich habe das ganze auch gerade als Aufgabe, jedoch möchte ich es nicht über das Scheibenmoment machen, sondern wirklich über die Zylinderkoordinaten.
Ich bin inzwischen soweit gekommen, dass ich gesagt habe
} \! r^3 \, \dd z dr )
und das z(r) hab ich dargestellt als
= r\cdot \frac{H}{R} )
dementsprechend das dz mit
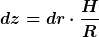
ersetzt. Das kommt daher, dass ich z/r = H/R gesetzt habe und dann umgestellt.
Wenn ich nun das 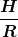 vor das Integral ziehe und dann integriere erhalte ich vor das Integral ziehe und dann integriere erhalte ich
 . .
Und wenn ichs dann entsprechend nochmal integriere
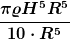
Dann kürzen sich die R raus...und dann steh ich da mit einem H^5 was mir überhaupt nix bringt...ich weiß nicht wo ich den fehler gemacht haben soll.
Hilfe!  |
|
 |
|


















