| Autor |
Nachricht |
Kira
Anmeldungsdatum: 29.09.2016
Beiträge: 6
|
 Kira Verfasst am: 08. Nov 2016 10:47 Titel: Trägheitsmoment verjüngter Stab Kira Verfasst am: 08. Nov 2016 10:47 Titel: Trägheitsmoment verjüngter Stab |
 |
|
Meine Frage:
Ich Frage mich wie man das Trägheitsmoment eines Stabs berechnen kann, bei dem die Masse nicht gleichmäßig verteilt ist, zum Beispiel bei einem verjüngten Stab.
Meine Ideen:
Ich kenne die Trägheitsmomente von gleichmäßigen Stäben und weiß wie man die je nach Drehachse verändert. Aber ich habe das Trägheitsmoment um die Schwerpunktachse nur bei normalen Stäben gefunden.
Vielleicht kann man einen verjüngten Stab auch als Kegel betrachten aber da habe ich das Trägheitsmoment nur für die Drehung um die eigene Achse und für eine Drehung um verschiedene Achsen wie beim Stab habe ich nichts gefunden.
MFG |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 08. Nov 2016 12:22 Titel: Mathefix Verfasst am: 08. Nov 2016 12:22 Titel: |
 |
|
Kennst Du die Herleitung des Massenträgheitsmoments?
Das kannst Du auf alle Schwerpunktachsen anwenden.
Geht die Bezugsachse nicht durch den Schwerpunkt, gilt der Satz von Steiner. |
|
 |
Kira
Anmeldungsdatum: 29.09.2016
Beiträge: 6
|
 Kira Verfasst am: 08. Nov 2016 12:47 Titel: Kira Verfasst am: 08. Nov 2016 12:47 Titel: |
 |
|
Also ich weiß nicht genau was du meinst.
Ich möchte den Kegel (also den sich verjüngenden Stab) um seine Außenachsen rotieren lassen, also einmal um die dicke und einmal um die dünne Seite und nicht um seine eigene Achse.
Für die Rotation um die eigene Achse steht bei Wikipedia 0,3mr^2 für das Trägheitsmoment eines Kegels.
Wenn ich ihn aber wie einen Stab um die Außenachsen rotieren lassen will, ist die neue achse nicht parallel und der steinersche Satz lässt sich nicht anwenden oder? |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 08. Nov 2016 12:49 Titel: GvC Verfasst am: 08. Nov 2016 12:49 Titel: |
 |
|

mit

Einsetzen:

Falls  : :
\, dr)
Hast Du ein konkretes Beispiel? |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 08. Nov 2016 13:03 Titel: Mathefix Verfasst am: 08. Nov 2016 13:03 Titel: |
 |
|
| Kira hat Folgendes geschrieben: | Also ich weiß nicht genau was du meinst.
Ich möchte den Kegel (also den sich verjüngenden Stab) um seine Außenachsen rotieren lassen, also einmal um die dicke und einmal um die dünne Seite und nicht um seine eigene Achse.
Für die Rotation um die eigene Achse steht bei Wikipedia 0,3mr^2 für das Trägheitsmoment eines Kegels.
Wenn ich ihn aber wie einen Stab um die Außenachsen rotieren lassen will, ist die neue achse nicht parallel und der steinersche Satz lässt sich nicht anwenden oder? |
Mach bitte eine Skizze und zeichne die Rotationsachsen ein. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 08. Nov 2016 13:40 Titel: Myon Verfasst am: 08. Nov 2016 13:40 Titel: |
 |
|
Die Beziehung
\,\mathrm{d}V)
(wobei r der Abstand ist zur Achse, worauf sich das Trägheitsmoment bezieht) gilt völlig allgemein für jeden Körper. Bei einem rotationssymmetrischen Körper bietet sich die Berechnung mit Zylinderkoordinaten an.
@GvC: Was ist A(r) in Deiner Rechnung? |
|
 |
Kira
Anmeldungsdatum: 29.09.2016
Beiträge: 6
|
 Kira Verfasst am: 08. Nov 2016 13:53 Titel: Kira Verfasst am: 08. Nov 2016 13:53 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | 
mit

Einsetzen:

Falls  : :
\, dr)
Hast Du ein konkretes Beispiel? |
Konkret möchte ich das Trägheitsmoment für einen Kegel mir Radius 2cm und einer Länge von 15cm herausfinden, wenn er um seine Achse am Dicken Ende rotiert. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 08. Nov 2016 14:13 Titel: Myon Verfasst am: 08. Nov 2016 14:13 Titel: |
 |
|
Ich bin jetzt nicht ganz sicher, was Du mit der "Achse am dicken Ende" meinst. Wenn es um die Achse durch die Kegelspitze geht, ergibt sich mit Zylinderkoordinaten

Im vorliegenden Fall mit r(z)=2-2z/15 gibt das
^4 \,\mathrm{d}z)
Zuletzt bearbeitet von Myon am 08. Nov 2016 14:44, insgesamt 2-mal bearbeitet |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 08. Nov 2016 14:35 Titel: Mathefix Verfasst am: 08. Nov 2016 14:35 Titel: |
 |
|
Kegel rotiert um die Basis ("dickes Ende")
 = r_0\cdot (1- \frac{y}{h} ))

) ^{2} \cdot \pi \cdot \varrho \cdot \dd y\cdot y^{2} )
) ^{2} \cdot y^{2} \, \cdot \dd y
<br />
)
Das Integral kannst Du bestimmt selber lösen. |
|
 |
-
Gast
|
 - Verfasst am: 08. Nov 2016 14:50 Titel: - Verfasst am: 08. Nov 2016 14:50 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | 
 |
Das ist leider nicht ganz korrekt. Nicht alle Punkte der Kegelscheibe mit Dicke dy haben den Abstand y von der Rotationsachse. Diese anderen Punkte haben einen größeren Abstand und tragen dementspechend mehr zum Trägheitsmoment bei. |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 08. Nov 2016 15:05 Titel: Mathefix Verfasst am: 08. Nov 2016 15:05 Titel: |
 |
|
| - hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | 
 |
Das ist leider nicht ganz korrekt. Nicht alle Punkte der Kegelscheibe mit Dicke dy haben den Abstand y von der Rotationsachse. Diese anderen Punkte haben einen größeren Abstand und tragen dementspechend mehr zum Trägheitsmoment bei. |
Wie bitte?
Das erklär mal!
Jede der "unendlich dünnen" Kegelscheiben hat den Abstand y von der Rotationsachse. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 08. Nov 2016 15:12 Titel: Myon Verfasst am: 08. Nov 2016 15:12 Titel: |
 |
|
|
@Mathefix: Nur damit keine Missverständnisse aufkommen, dieser "Gast" von vorhin war nicht ich. Was aber richtig ist, dass Du eine Integration von 0 bis zum Radius über r^2 ausführen musst, was bei Dir gar nicht vorkommt. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 08. Nov 2016 15:48 Titel: GvC Verfasst am: 08. Nov 2016 15:48 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | @GvC: Was ist A(r) in Deiner Rechnung? |
Für die Rotation um die Achse am dicken Ende:
=\pi\cdot R^2\cdot\left(1-\frac{r}{l}\right)^2)
Für die Rotation um die Achse an der Spitze:
=\pi\cdot R^2\cdot\left(\frac{r}{l}\right)^2)
Dabei ist R der Radius des Kegelgrundkreises. Integriert wird dann von r=0 bis r=l mit l=Länge des kegelförmigen Stabes. |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 08. Nov 2016 15:51 Titel: Mathefix Verfasst am: 08. Nov 2016 15:51 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | @Mathefix: Nur damit keine Missverständnisse aufkommen, dieser "Gast" von vorhin war nicht ich. Was aber richtig ist, dass Du eine Integration von 0 bis zum Radius über r^2 ausführen musst, was bei Dir gar nicht vorkommt. |
Wie das denn?
Ich integriere von y=0 bis y=h
Wenn ich über r (r=0 bis r=r_0) integriere, hätte ich einen Ansatz über Hohlzylinder
)
gemacht. |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 08. Nov 2016 15:53 Titel: Mathefix Verfasst am: 08. Nov 2016 15:53 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | | Myon hat Folgendes geschrieben: | | @GvC: Was ist A(r) in Deiner Rechnung? |
Dabei ist R der Radius des Kegelgrundkreises. Integriert wird dann von r=0 bis r=l mit l=Länge des kegelförmigen Stabes. |
r = l ??? |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 08. Nov 2016 16:09 Titel: GvC Verfasst am: 08. Nov 2016 16:09 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | | r = l ??? |
Wieso fragst Du?
In der Formel

ist r der Abstand von der Drehachse. Mit "meinem" A(r) ergibt sich übrigens dasselbe Ergebnis wie das in Deinem Beitrag von 14.35 Uhr hergeleitete (nur mit anderen Bezeichnungen, "Dein" y ist "mein" r, Dein r0 ist mein R, Dein h ist mein l). Ich verstehe deshalb nicht, was Du dagegen hast. Oder bist Du mittlerweile zu einer anderen Überzeugung als um 14.35 Uhr gelangt? |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 08. Nov 2016 16:51 Titel: Myon Verfasst am: 08. Nov 2016 16:51 Titel: |
 |
|
Rechnen wir alle doch mal explizit das Trägheitsmoment für das Beispiel aus, dann können wir vergleichen. Ich erhalte
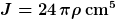 |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 08. Nov 2016 17:34 Titel: GvC Verfasst am: 08. Nov 2016 17:34 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | Rechnen wir alle doch mal explizit das Trägheitsmoment für das Beispiel aus, dann können wir vergleichen. Ich erhalte
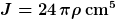 |
Normalerweise wird das Trägheitsmoment von Stäben für die Rotation um eine Achse senkrecht zur Stabachse angegeben als

Im vorliegenden Fall ergibt sich der Faktor k bei Rotation um die Achse am dicken Ende zu k=0,1 und bei Rotation um die Achse an der Spitze zu k=0,6. Dein Ergebnis stimmt mit meinem nicht überein. Du hast allerdings auch eine andere Bestimmungsformel für J verwendet, deren Herleitung ich übrigens nicht nachvollziehen kann.
Wenn ich das Trägheitsmoment für Rotation um die Achse am dicken Ende in Deinem Standard darstelle, dann ist das

Zuletzt bearbeitet von GvC am 08. Nov 2016 17:55, insgesamt einmal bearbeitet |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 08. Nov 2016 17:49 Titel: Myon Verfasst am: 08. Nov 2016 17:49 Titel: |
 |
|
Ich weiss nicht, welche Bestimmungsformel Du meinst. Mein Ergebnis stimmt überein mit tabellierten Werten für einen Kegel
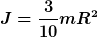 . .
Ehrlich gesagt kann ich Deine Rechnung nicht nachvollziehen, oder zumindest nicht, wie man damit das Trägheitsmoment im vorliegenden Fall explizit ausrechnen kann. Bei Mathefix geht die Höhe hoch 3 ins Trägheitsmoment ein, was auch nicht sein kann.
| GvC hat Folgendes geschrieben: | Wenn ich das Trägheitsmoment für Rotation um die Achse am dicken Ende in Deinem Standard darstelle, dann ist das
 |
Da kann ich gar nicht mehr folgen. Es geht nicht um das Trägheitsmoment am einen oder anderen Ende, sondern um den ganzen Kegel. Das habe ich (meiner Ansicht nach korrekt) über Zylinderkoordinaten berechnet, siehe oben. Welches Trägheitsmoment erhältst denn Du? |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 08. Nov 2016 18:19 Titel: GvC Verfasst am: 08. Nov 2016 18:19 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | Ich weiss nicht, welche Bestimmungsformel Du meinst. |
Na ja, ich meine natürlich diejenige, die Du um 14.13 Uhr gepostet hast.
| Myon hat Folgendes geschrieben: |
^4 \,\mathrm{d}z) |
| Zitat: | Mein Ergebnis stimmt überein mit tabellierten Werten für einen Kegel
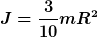 |
Kann es sein, dass Du das Trägheitsmoment für die Rotation um die Symmetrieachse des Kegels bestimmt hast. Das entspricht aber nicht der Aufgabenstellung. Danach soll das Trägheitsmoment um eine Achse bestimmt werden, die senkrecht auf der Symmetrieachse steht, und zwar für zwei Fälle, nämlich Drehachse an der Grundfläche und Drehachse an der Spitze des Kegels. Das ist ähnlich wie beim Stab mit konstantem Querschnitt bei Rotation um eine zur Symmetrieachse senkrechte Achse am Stabende, bei dem die Tabelle ein Trägheitsmoment von J=(1/3)ml² ausweist. Im vorliegenden Fall ist jedoch die Querschnittsfläche des Stabes nicht konstant. Für eine solche Form ist das Trägheitsmoment um eine Achse am Stabende nicht tabelliert. Deshalb hat Kira ja nachgefragt.
| Kira hat Folgendes geschrieben: | Vielleicht kann man einen verjüngten Stab auch als Kegel betrachten aber da habe ich das Trägheitsmoment nur für die Drehung um die eigene Achse und für eine Drehung um verschiedene Achsen wie beim Stab habe ich nichts gefunden.
|
| Myon hat Folgendes geschrieben: | | Welches Trägheitsmoment erhältst denn Du? |
Habe ich doch geschrieben:
| GvC hat Folgendes geschrieben: |  |
was dasselbe ist wie
 |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 08. Nov 2016 18:38 Titel: Myon Verfasst am: 08. Nov 2016 18:38 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | | Kann es sein, dass Du das Trägheitsmoment für die Rotation um die Symmetrieachse des Kegels bestimmt hast |
Selbstverständlich habe ich das. Nun wird mir einiges klar. 
Das Trägheitsmoment senkrecht zur Symmetrieachse ist beim Kegel viel schwieriger zu berechnen und ist m.E. nicht auf Deine Weise möglich. Was Mathefix und Du berechnet habt, wäre das Trägheitsmoment eines rotierenden Dreiecks. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 08. Nov 2016 18:42 Titel: GvC Verfasst am: 08. Nov 2016 18:42 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | Was Mathefix und Du berechnet habt, wäre das Trägheitsmoment eines rotierenden Dreiecks. |
Das ist Quatsch. Schau Dir das ruhig nochmal genau an. |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 08. Nov 2016 18:47 Titel: Mathefix Verfasst am: 08. Nov 2016 18:47 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | | r = l ??? |
Wieso fragst Du?
In der Formel

ist r der Abstand von der Drehachse. Mit "meinem" A(r) ergibt sich übrigens dasselbe Ergebnis wie das in Deinem Beitrag von 14.35 Uhr hergeleitete (nur mit anderen Bezeichnungen, "Dein" y ist "mein" r, Dein r0 ist mein R, Dein h ist mein l). Ich verstehe deshalb nicht, was Du dagegen hast. Oder bist Du mittlerweile zu einer anderen Überzeugung als um 14.35 Uhr gelangt? |
Die y-Richtung mit r zu bezeichnen hat mich wohl verwirrt.
Ansonsten sind wir einig.
Es gibt eben drei Möglichkeiten die Masse des Kegels zu bestimmen, über
1. Kreisscheibe
2. Hohzylinder
3. Würfel |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 08. Nov 2016 18:58 Titel: Myon Verfasst am: 08. Nov 2016 18:58 Titel: |
 |
|
@GvC: Lassen wir das mal mit dem Quatsch. Wir haben hier nicht die gleiche Meinung, und es ist selbstverständlich immer möglich, dass ich mich irre.
Ich habe Eure Rechnung versucht nachzuvollziehen, und ich bleibe dabei. Es wird hier das Trägheitsmoment eines Dreiecks berechnet. Bei einem Kegel ist dies viel schwieriger, und sonst verstehen wir unter einem Kegel nicht das Gleiche. Wo geht denn z.B. bei Eurer Rechnung die kreisförmige Grundfläche ein? Wie berechnet Ihr bei jedem Volumenenlement den Abstand zur Achse? |
|
 |
LilaLumis
Gast
|
 LilaLumis Verfasst am: 08. Nov 2016 19:14 Titel: LilaLumis Verfasst am: 08. Nov 2016 19:14 Titel: |
 |
|
| Myon hat Folgendes geschrieben: |
Das Trägheitsmoment senkrecht zur Symmetrieachse ist beim Kegel viel schwieriger zu berechnen |
Ja etwas
 |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 08. Nov 2016 19:29 Titel: Myon Verfasst am: 08. Nov 2016 19:29 Titel: |
 |
|
@LilaLumis: Wahrscheinlich darf man gratulieren. Ich versuchs später auch noch auszurechnen. Da ich aufgrund von äusseren Umständen nicht so einfach mit Papier und Schreiber herumrechnen kann, geht es vielleicht etwas länger. Bis dahin bitte nicht verraten, wie Du das Integral aufgestellt hast.  |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 08. Nov 2016 19:32 Titel: Mathefix Verfasst am: 08. Nov 2016 19:32 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | @GvC: Lassen wir das mal mit dem Quatsch. Wir haben hier nicht die gleiche Meinung, und es ist selbstverständlich immer möglich, dass ich mich irre.
Ich habe Eure Rechnung versucht nachzuvollziehen, und ich bleibe dabei. Es wird hier das Trägheitsmoment eines Dreiecks berechnet. Bei einem Kegel ist dies viel schwieriger, und sonst verstehen wir unter einem Kegel nicht das Gleiche. Wo geht denn z.B. bei Eurer Rechnung die kreisförmige Grundfläche ein? Wie berechnet Ihr bei jedem Volumenenlement den Abstand zur Achse? |
Schau Dir mal die Herleitung von GvC und mir genau an:
in 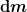 steckt über steckt über  der zur Rotationsachse parallele Kreisquerschnitt des Kegels. Es wird also nicht ein flaches Dreieck sondern ein Körper betrachtet. der zur Rotationsachse parallele Kreisquerschnitt des Kegels. Es wird also nicht ein flaches Dreieck sondern ein Körper betrachtet.
Vielleicht macht Dir ein anderer Ansatz das klarer:
Nach der Guldin´schen Regel zerlegen wir den Kegel in Hohzylinder
) |
|
 |
LilaLumis
Gast
|
 LilaLumis Verfasst am: 08. Nov 2016 20:48 Titel: LilaLumis Verfasst am: 08. Nov 2016 20:48 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | @LilaLumis: Wahrscheinlich darf man gratulieren |
Nee
Inzwischen habe ich

Hätte ich doch bloß aufgehört |
|
 |
LilaLumis
Gast
|
 LilaLumis Verfasst am: 08. Nov 2016 21:06 Titel: LilaLumis Verfasst am: 08. Nov 2016 21:06 Titel: |
 |
|

Das ist die Lösung
Jetzt seid ihr am Zug |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 08. Nov 2016 23:51 Titel: Myon Verfasst am: 08. Nov 2016 23:51 Titel: |
 |
|
Hmm... Ich komm einfach nicht auf das...
Hier meine allgemeine Lösung:
}\int_0^{2\pi}\,(z^2+r^2\sin^2\varphi)\,r\,\mathrm{d}\varphi\,\mathrm{d}r\,\mathrm{d}z)
Wofür ich nach einigem Rechnen
)
erhalte.
Mit den Zahlen des Beispiels ergäbe dies
 . .
Wie sieht Deine allgemeine Lösung aus, LilaLumis? Wo hab ich mich womöglich verrechnet? |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 09. Nov 2016 00:41 Titel: VeryApe Verfasst am: 09. Nov 2016 00:41 Titel: |
 |
|
Ich würde vorschlagen bevor hier jeder irgendwas durcheinander berechnet, sicher zu stellen, das jeder überhaupt auch das gleiche Szenario berechnet.
was soll das überhaupt sein. Rotation um das dicke Ende, ist für mich nichtssagend.
Eine Skizze kann ja nicht so schwer sein oder?
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 09. Nov 2016 01:40 Titel: Myon Verfasst am: 09. Nov 2016 01:40 Titel: |
 |
|
| LilaLumis hat Folgendes geschrieben: | 
Das ist die Lösung
Jetzt seid ihr am Zug |
Nachdem ich endlich einen saudummen Rechenfehler entdeckt habe, komme ich auch auf dieses Ergebnis.
Hier die allgemeine Lösung, wenn es jemanden interessiert:
}\int_0^{2\pi}\,(z^2+r^2\sin^2\varphi)\,r\,\mathrm{d}\varphi\,\mathrm{d}r\,\mathrm{d}z)
}\,\left[z^2\varphi+r^2(\frac{1}{2}(\varphi-\sin\varphi\cos\varphi))\right]_{\varphi=0}^{\varphi=2\pi}\,r\,\mathrm{d}r\,\mathrm{d}z)
}\,(2z^2+r^2)\,r\,\mathrm{d}r\,\mathrm{d}z)
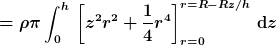
^2+\frac{1}{4}(R-Rz/h)^4\right)\,\mathrm{d}z)
^4\right)\,\mathrm{d}z)
)
)
oder
)
Mit den Werten für R und h eingesetzt wie im Beispiel kommt man auf das Ergebnis von LilaLumis.
@VeryApe: Es geht um das Trägheitsmoment eines Kegels bezüglich der Achse, die durch den Mittelpunkt der Grundfläche geht und senkrecht auf der Symmetrieachse steht. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 09. Nov 2016 01:55 Titel: GvC Verfasst am: 09. Nov 2016 01:55 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | ...
Hier die allgemeine Lösung, wenn es jemanden interessiert:
...
}\int_0^{2\pi}\,(z^2+r^2\sin^2\varphi)\,r\,\mathrm{d}\varphi\,\mathrm{d}r\,\mathrm{d}z)
...
) |
Wie kann das denn sein? Hier hat J die Dimension Länge^5. Ein Trägheitsmoment muss aber die Dimension Masse*Länge² haben.
| Myon hat Folgendes geschrieben: | oder
)
|
Das kann ich nicht nachvollziehen. Es muss sich eine Lösung der Form

ergeben.
Zuletzt bearbeitet von GvC am 09. Nov 2016 01:59, insgesamt einmal bearbeitet |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 09. Nov 2016 02:19 Titel: Myon Verfasst am: 09. Nov 2016 02:19 Titel: |
 |
|
Das Trägheitsmoment soll unabhängig vom Radius sein? Das wäre seltsam. Dank Google gefunden: Das obige Ergebnis stimmt mit dem hier angegebenen Trägheitsmoment überein (siehe S. 4).
Zur Dimension: ich hatte für einen Augenblick die Dichte vergessen, dies dann aber schnell korrigiert. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 09. Nov 2016 10:00 Titel: VeryApe Verfasst am: 09. Nov 2016 10:00 Titel: |
 |
|
Myon 
Ich erhalte

Ich habe den Zylinder in Kreisscheiben zerlegt.
für eine unendlich dünne Kreisscheibe die um ihren Massenmittelpunkt rotiert

das kann man sich ableiten oder man nimmt die formel für einen Vollzylinder der um eine Querachse rotiert und da ist die Formel siehe wiki

und daher

da dm dy² kleiner als unendlich klein zum quadrat ist kann man das in die Mülltone werfen

bezüglich der Drehachse verschiebt sich das Trägheitsmoment um

die Masse einer unedlich dünnen Kreissscheibe


mit der richtigen Formel von Mathefix für den Radius
)
^{4}*dy+\varrho *\pi *r_{0}²*(1-\frac {y}{h})²*y²*dy )
^{4}*dy+ \varrho *\pi *r_{0}² \int^h_0 (1-\frac {y}{h})²*y²*dy )
wenn mathefix das gleiche berechnen wollte wie myon dann berücksichtigt er nicht die Eigendrehung der Kreischeiben um ihren eigenen Massenmittelpunkt.
Mann kann die Kreischeiben betrachten wie wenn sie sich translatorisch auf unterschiedlichen kreisbahnen um die Drehachse bewegen, dabei bleibt ihre Ausrichtung im Raum gleich (Steinerverschiebesatz), und dann müssen sie sich noch um ihre eigene Massenmittelpunktsachse drehen (trägheistmoment um den Schwerpunkt).
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 09. Nov 2016 11:35 Titel: Myon Verfasst am: 09. Nov 2016 11:35 Titel: |
 |
|
|
@VeryApe: Ja, die Überlegung, den Satz von Steiner auf jedes Volumenelement (Kreisscheibe) anzuwenden, führt ebenfalls zum Ziel. Und erfreulicherweise kommt offenbar dasselbe heraus dabei! |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 09. Nov 2016 12:17 Titel: GvC Verfasst am: 09. Nov 2016 12:17 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | Das Trägheitsmoment soll unabhängig vom Radius sein? Das wäre seltsam. |
Nicht so sehr, wenn man die Berechnung des Trägheitsmomentes für einen dünnen Stab vor Augen hat, das auch unabhängig vom Radius ist. Das war übrigens der Grund für meinen Berechnungsansatz. Dabei hatte ich mich von der Wortwahl des Fragestellers beeinflussen lassen, der von einem sich verjüngenden Stab sprach. Die später nachgelieferten Maße für ein konkretes Beispiel habe ich dann nicht mehr hinterfragt. Sie zeigen, dass es sich bei dem konkreten Beispiel nicht mehr um einen Stab im engeren Sinne handelt. Dennoch ist die Abweichung des nach "meinem" vereinfachten Verfahren berechneten Trägheitsmomentes von dem genaueren Wert nach "Deinem" Verfahren weniger als 3%. Wäre der Radius in dem vorliegenden Beispiel nur halb so groß wie hier vorgegeben, wäre die Abweichung nur noch 2 Promille. Zusammenfassend lässt sich aus meiner Sicht sagen, dass Deine Berechnung die richtige ist, mein vereinfachtes Verfahren aber durchaus eine gewisse Berechtigung hat. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 09. Nov 2016 12:29 Titel: Myon Verfasst am: 09. Nov 2016 12:29 Titel: |
 |
|
|
Es geht ja nicht darum, wer mehr oder weniger "recht" hat, Hauptsache, man nähert sich der Lösung. Die Abweichung ist hier tatsächlich klein, da das Verhältnis h/R gross ist und in diesem Fall v.a. die Kegelspitze zum Trägheitsmoment beiträgt. Bei einem stumpfen Kegel sähe es anders aus. |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 09. Nov 2016 13:51 Titel: Mathefix Verfasst am: 09. Nov 2016 13:51 Titel: |
 |
|
|
Die Ursache dieser ausufernden Diskussion um die richtige Lösung liegt darin, dass wegen unklar formulierter Aufgabenstellung "Rotation um dicke Seite, dünne Seite" und fehlender Skizze jeder etwas anderes versteht. Insofern hat jeder recht. |
|
 |
|

















