| Autor |
Nachricht |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 08. Dez 2008 21:47 Titel: Höhenberechnung Wasserspiegel in Kegel Sonex Verfasst am: 08. Dez 2008 21:47 Titel: Höhenberechnung Wasserspiegel in Kegel |
 |
|
Das ist schon relataiv die Endformel für die Höhen Brechnung des Wasserspiegels nach Zeit h(t) wenn im Kegel unten eine Öffnung mit r ist und wasser hinaus fließt... ist ds soweit schon richtrig?
und
}{h_{0}}]^4* \pi ^2 -A_{1}^2}}{\sqrt{h}}*dh=-\sqrt{2*g}*A_{1}dt)
}_{h_{0}}\sqrt{\frac{[r+\frac{h(R-r)}{h_{0}}]^4* \pi ^2 -A_{1}^2}{h}}*dh=-\sqrt{2*g}*A_{1}\int\limits^{t}_{0}dt)
}_{h_{0}}\sqrt{\frac{[r+\frac{h(R-r)}{h_{0}}]^4* \pi ^2 -A_{1}^2}{h}}*dh=-\sqrt{2*g}*A_{1}t)
}_{h_{0}}\sqrt{\frac{[r+\frac{h(R-r)}{h_{0}}]^4* \pi ^2 -A_{1}^2}{h}}*dh=-\sqrt{2*g}*A_{1}t)
müsste ich erst das Integral von der linken seite lösen?
oder gibt es ne einfachere variante um später nach t um zu stellen...
wenn ich zahlen einsetzen bis auf das h natürlich dann integriere (ingtegral von 10 bis 0) dann erhalte ich ca. = 12402 das habe ich dann durch die rechte seite geteilt (so das t übrig bleibt.. und erhalte 35,65 s
also
}_{h_{0}}\sqrt{\frac{[r+\frac{h(R-r)}{h_{0}}]^4* \pi ^2 -A_{1}^2}{h}}*dh}{-\sqrt{2*g}*A_{1}}=t)
}{10}]^4* 3,14 ^2 -(3,14*5^2)^2}{h}}*dh}{-\sqrt{2*9,81}*(3,14*5^2)}=t)
zur not könnte ich die Aufgabenstellung noch mit hineinbringen....
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. Dez 2008 03:22 Titel: dermarkus Verfasst am: 09. Dez 2008 03:22 Titel: |
 |
|
Wenn du die Aufgabenstellung mit angibst und außerdem noch dazuschreibst, mit welchen Ansätzen und Überlegungen du auf deine "fast-schon-Endformel" gekommen bist, würde das natürlich den Helfenden das Nachvollziehen und Helfen erleichtern.
Was meinst du übrigens mit "Zahlen einsetzen"? Haben die Angaben aus der Aufgabenstellung und die zugehörigen Ergebnisse keine Einheiten?
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. Dez 2008 14:19 Titel: dermarkus Verfasst am: 09. Dez 2008 14:19 Titel: |
 |
|
Mit
| Sonex hat Folgendes geschrieben: |
=r+\frac{h(R-r)}{h_{0}})
|
bin ich einverstanden, ebenso mit der Idee, dass man die am Ende entstehende Differentialgleichung für h(t) prima mit Separation der Variablen lösen können wird.
Ob allerdings die Formeln
| Zitat: |
=>aus den allgemeinen Formel v1*Ar=v2*Ah und
|
und
| Zitat: |
^2}})
|
hier zutreffen, bin ich mir allerdings nicht mehr sicher.
Was genau meinst du mit 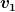 ? ?
Ist die Ausflussgeschwindigkeit unten am Loch nicht vielmehr einfach nach Torricelli gleich }) ? ?
Mit dem Ansatz, dass die Wasservolumenabnahme im Trichter gleich schnell erfolgt wie das Wasserausfließen unten am Loch (gleich viel Volumen pro Zeit), komme ich am Ende auf eine andere Gleichung als du.
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 09. Dez 2008 15:17 Titel: Sonex Verfasst am: 09. Dez 2008 15:17 Titel: |
 |
|
Mit v1 meine ich die Geschwindigkeit die die Flüssigkeit hat beim auslaufen... und die ist doch nicht konstant... so dachte ich muss ich v1 bilden.... also v ist abhänhängig von h(t) so bekommt man v1....
das was ja auch zu nächst mein ansatz mit der Formel von Torricelli...
aber weiß ich nicht genau wie man da angehen soll da ja dann nach meiner meinung v=konst wäre...
also habe nun bissle den Faden jetzt verloren
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. Dez 2008 17:07 Titel: dermarkus Verfasst am: 09. Dez 2008 17:07 Titel: |
 |
|
| Sonex hat Folgendes geschrieben: | Mit v1 meine ich die Geschwindigkeit die die Flüssigkeit hat beim auslaufen... und die ist doch nicht konstant...
.... also v ist abhänhängig von h(t)
das was ja auch zu nächst mein ansatz mit der Formel von Torricelli...
|
Einverstanden.
Also })
Wo siehst du da noch ein Problem? In dieser Formel steckt all das, wovon du gesprochen hast.
------------------------
Wenn du mit diesem 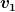 die Geschwindigkeit des Wassers am Ausfluss meinst und mit die Geschwindigkeit des Wassers am Ausfluss meinst und mit 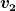 die Geschwindigkeit, mit der sich die Wasseroberfläche im Trichter senkt, dann bin ich auch damit einverstanden, dass du zum Beispiel die Formel die Geschwindigkeit, mit der sich die Wasseroberfläche im Trichter senkt, dann bin ich auch damit einverstanden, dass du zum Beispiel die Formel
) A_r = v_2(h(t)) A_h(h(t)))
nehmen kannst, um anzusetzen, dass das ausfließende Wasservolumen pro Zeit gleich der Abnahme des Wasservolumens pro Zeit im Trichter ist.
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 09. Dez 2008 17:46 Titel: Sonex Verfasst am: 09. Dez 2008 17:46 Titel: |
 |
|
sieht dann die neue so aus:
jetzt blick cih nciht mehr durch...
) )
)=\frac{A_{r}}{A(h(t))}*\sqrt{2gh(t)})
aber wie bekomme ich h(t)
Zuletzt bearbeitet von Sonex am 09. Dez 2008 20:55, insgesamt einmal bearbeitet |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. Dez 2008 17:51 Titel: dermarkus Verfasst am: 09. Dez 2008 17:51 Titel: |
 |
|
Da ist sehr vieles richtig, nur in
| Sonex hat Folgendes geschrieben: |
) )
|
hast du noch etwas vergessen. Denn im Moment schreibst du da links noch eine Strecke hin, während rechts eine Geschwindigkeit steht.
Die Differentialgleichung für das h(t) löst du am Ende einfach wieder durch Separation der Variablen.
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 09. Dez 2008 18:20 Titel: Sonex Verfasst am: 09. Dez 2008 18:20 Titel: |
 |
|
}{dt}=-v(h(t)) )
}{dt}=-\frac{A_{r}}{[r+\frac{h(t)(R-r)}{h_{0}}]^2*\pi}*\sqrt{2gh(t)} )
dann müsste ich doch nur noch das Integral bilden... wenn alles (hoffe) berücksichtigt ist...
=-\frac{A_{r}*\sqrt{2gh(t)}}{[r+\frac{h(t)(R-r)}{h_{0}}]^2*\pi}dt )
=-\frac{A_{r}*\sqrt{2gh(t)}}{[r+\frac{h(t)(R-r)}{h_{0}}]^2*\pi}\int\limits^{t}_{0}dt )
(R-r)}{h_{0}}]^2*\pi}{A_{r}*\sqrt{2gh(t)}}dh)
}_{h_{0}} \frac{[r+\frac{h(t)(R-r)}{h_{0}}]^2*\pi}{A_{r}*\sqrt{2gh(t)}}dh)
(R-r)}{h_{0}}]^2*\pi}{A_{r}*\sqrt{2gh(t)}})
dann bekomme ich ca. t=4,8s raus
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. Dez 2008 23:16 Titel: dermarkus Verfasst am: 09. Dez 2008 23:16 Titel: |
 |
|
Bis
| Sonex hat Folgendes geschrieben: |
(R-r)}{h_{0}}]^2*\pi}{A_{r}*\sqrt{2gh(t)}})
|
bin ich noch einverstanden. (Auch wenn ich finde, dass du die Zwischenschritte noch nicht ganz sauber aufgeschrieben und das Vorzeichen für t noch nicht richtig durchgezogen hast)
Aber ich bekomme für die Zeit t einen anderen Wert als
| Zitat: |
dann bekomme ich ca. t=4,8s raus |
heraus.
Magst du am besten mal zeigen, wie du dein Integral ausrechnest, und was dabei als Endergebnis-Formel für  herauskommt, bevor du die konkreten Werte für herauskommt, bevor du die konkreten Werte für 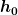 , ,  und und  darin einsetzt? darin einsetzt?
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 11:17 Titel: Sonex Verfasst am: 10. Dez 2008 11:17 Titel: |
 |
|
(R-r)}{h_{0}}]^2*\pi}{A_{r}*\sqrt{2gh(t)}})
(R-r)}{h_{0}}]^2*\pi}{(R^2*\pi)_{r}*\sqrt{2gh(t)}})
(R-r)}{h_{0}}]^2}{R^2*\sqrt{2gh(t)}})
(R-r)}{h_{0}}]^2}{R^2*\sqrt{2gh(t)}})
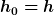
(15 h^2 r^2 -10 h(r-R)h(t)r+3(r-R)^2h^2(t))}{15h^2 \sqrt{gh(t)}}|_{10}^{0} )
*10*r+3(r-R)^2*10^2)}{15h^2 \sqrt{g*10}} )
*10*0,25+3(0,25-5)^2*10^2)}{15*10^2 \sqrt{981*10}} )
soweit richtig??? doch dann erhalten ich noch nicht mal ne Sekunde...

|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Dez 2008 16:00 Titel: dermarkus Verfasst am: 10. Dez 2008 16:00 Titel: |
 |
|
Tipps:
* Achte beim Aufschreiben darauf, dass du nicht einfach irgendwo Sachen vergisst. In
| Sonex hat Folgendes geschrieben: | (R-r)}{h_{0}}]^2*\pi}{A_{r}*\sqrt{2gh(t)}})
|
fehlt das 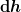 am Ende, das zeigt, worüber integriert wird. am Ende, das zeigt, worüber integriert wird.
* Was hast du denn da für das  eingesetzt? Sag nochmal ganz genau, was du mit dem eingesetzt? Sag nochmal ganz genau, was du mit dem  meinst, und durch welchen Formelausdruck du es folglich darstellen musst. meinst, und durch welchen Formelausdruck du es folglich darstellen musst.
* Rechne auch bei den Integralgrenzen erstmal nur mit Variablen und nicht mit Zahlen. Schreibe also nicht 10 und 0, sondern 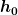 und 0 und 0
| Zitat: |
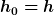
|
 Hoppla, was soll denn das?? Hoppla, was soll denn das?? 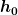 ist nicht gleich ist nicht gleich 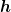 . .
Wiederhole unbedingt nochmal ganz dringend, was Integrieren überhaupt ist und wie das geht.
Übungsaufgabe für dich: Berechne das Integral

Und schreibe jeden Rechenschritt für die Berechnung dieses Integrals sauber auf.
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 16:13 Titel: Sonex Verfasst am: 10. Dez 2008 16:13 Titel: |
 |
|
Das ist ja nicht so das Problem... nur die da oben ist ja wohl wesentlich komplexer....

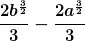
Die Fläche Ar habe ich verwechselt und ist die Fläche unten am Kegel....
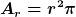
(R-r)}{h_{0}}]^2*\pi}{r^2 \pi*\sqrt{2gh(t)}}dh(t))
(R-r)}{h_{0}}]^2}{r^2 *\sqrt{2gh(t)}}dh(t))
Zuletzt bearbeitet von Sonex am 10. Dez 2008 16:33, insgesamt einmal bearbeitet |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Dez 2008 16:23 Titel: dermarkus Verfasst am: 10. Dez 2008 16:23 Titel: |
 |
|
Das hast du zwar schon richtig berechnet, aber noch nicht sauber aufgeschrieben. Spätestens wenn das Integral mal ein bisschen größer wird, brauchst du aber unbedingt eine saubere Darstellung, damit du den Überblick behalten kannst und auch das komplizierte Integral genauso leicht lösen kannst wie so ein "kleineres und einfacheres".
Wie schreibst du deine Lösung für das Übungsbeispiel sauber auf?
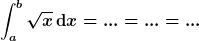
(Und kannst du zum Beispiel zusätzlich noch in Worten dazusagen, was du da jeweils tust?)
Und wie lautet die Lösung für das Integral aus deiner Aufgabe, wenn du es ebenfalls sauber aufschreibst und ebenso sorgfältig die Schritte für das Integrieren durchführst wie in dem kleinen Übungsbeispiel?
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 16:48 Titel: Sonex Verfasst am: 10. Dez 2008 16:48 Titel: |
 |
|
Aber wie weit bringt mich das zur Lösung von da oben...
ich finde das Integral von da oben ein ganz schönen Hammer... da wenn ich richtig denke alle Integralregel vorkommen die es gibt... da wir einen bruch haben.. addition... multiplikation....
da ist die Kette nachher extrem lang... oder sehe ich das falsch...
Eigentlich verstehe ich nicht wieso man eine Aufgabe bekommt mit so einen komplexen Integral... in der Prüfung würde doch auch nicht sowas vorkommen????
kann es trotzdem sein des wesentlich unter 1 s raus kommt....
Zuletzt bearbeitet von Sonex am 10. Dez 2008 17:12, insgesamt einmal bearbeitet |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Dez 2008 17:02 Titel: dermarkus Verfasst am: 10. Dez 2008 17:02 Titel: |
 |
|
| Sonex hat Folgendes geschrieben: |
ich finde das Integral von da oben ein ganz schönen Hammer... da wenn ich richtig denke alle Integralregel vorkommen die es gibt... da wir einen bruch haben.. addition... multiplikation....
|
Wichtiger Tipp: Erstmal immer vereinfachen, so weit es geht. Und so übersichtlich wie möglich hinschreiben. Dann merkst du schnell, dass da in dem Integral eigentlich nichts anderes als eine Summe drinsteht.
| Zitat: |
Eigentlich verstehe ich nicht wieso man eine Aufgabe bekommt mit so einen komplexen Integral... in der Prüfung würde doch auch nicht sowas vorkommen???? |
* Dieses Integral ist überhaupt nicht kompliziert. Mit Schulwissen musst du das locker hinbekommen können. Auch in einer Klausur.
* Wenn dir bisher noch lange Formeln mit vielen Buchstaben drin Respekt einflößen, dann musst du unbedingt noch etwas für deine Mathe-Fitness tun. Denn beim Physikstudieren wirst du es noch mit viel längeren Formeln und Rechnungen zu tun bekommen.
// edit: Mit deiner Korrektur für das  bin ich einverstanden bin ich einverstanden 
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 18:00 Titel: Sonex Verfasst am: 10. Dez 2008 18:00 Titel: |
 |
|
Also ich kann veranfachen wie ich will.. nen Bruch habe ich trotzdem noch....
(R-r)]^2=[r+\frac{h(t)(R-r)}{h_{0}}]^2*\pi)
(R-r)}{h_{0}}]^2*\pi}{r^2 \pi*\sqrt{2gh(t)}}dh(t))
(R-r)]^2}{r^2 h_{o} \sqrt{2gh(t)}}dh(t))
oder durch raus ziehen
(R-r)]^2}{\sqrt{h(t)}}dh(t))
(R-r)]^2 h^{-\frac{1}{2}}(t)dh(t))
Zuletzt bearbeitet von Sonex am 10. Dez 2008 18:15, insgesamt 2-mal bearbeitet |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Dez 2008 18:14 Titel: dermarkus Verfasst am: 10. Dez 2008 18:14 Titel: |
 |
|
Weiter so  Du hast noch längst nicht zu Ende vereinfacht Du hast noch längst nicht zu Ende vereinfacht 
(Und denk dran, dass du für die Integralgrenzen die Variablen schreiben wolltest und noch nicht die eingesetzten Zahlen dafür.)
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 18:24 Titel: Sonex Verfasst am: 10. Dez 2008 18:24 Titel: |
 |
|
ist das richtig... wenn ich das im Taschenrechner Eingebe erhalte ich aufgerundet 2,2 s... das ist zummindest schon mal ein Prüf ergebnis habe wenn ich dann mein integral ausgerechnet habe
}_{h_{0}}- h(t)^3R^2 h^{-\frac{1}{2}}(t)-3 h_{0} r h(t) R h^{-\frac{1}{2}}(t)+2 r h^2(t) R h^{-\frac{1}{2}}(t)-r^2 h^2(t) h^{-\frac{1}{2}}(t)+2 h_{o} r^2 h(t) h^{-\frac{1}{2}}(t)-h_{0}^2 r^2 h^{-\frac{1}{2}}(t)dh(t))
}_{h_{0}}- h(t)^{\frac{5}{2}}R^2 -3 h_{0} r h(t)^{\frac{1}{2}} R +2 r R h^{\frac{3}{2}}(t)-r^2 h^{\frac{3}{2}}(t)+2 h_{o} r^2 h^{\frac{1}{2}}(t)-h_{0}^2 r^2 h^{-\frac{1}{2}}(t)dh(t))
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Dez 2008 18:32 Titel: dermarkus Verfasst am: 10. Dez 2008 18:32 Titel: |
 |
|
Drei Sachen dazu:
* Wenn du eine Summe im Integral stehen hast, musst du nun natürlich Klammern drumherum machen, damit es stimmt.
* Deine obere Integralgrenze stimmt nicht. Das Integral geht von 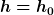 bis bis 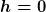 . .
* Dass das h von der Zeit abhängen soll, weißt du ja nun. Du könntest also statt h(t) einfach auch überall h schreiben.
* Du hast das ganze jetzt komplett in ganz viele einzelne Summanden unterteilt. Einige dieser Summanden hättest du gar nicht extra ausrechnen müssen, um das Integral nachher leicht lösen zu können. Denn alles, was sowieso nur Konstanten enthält, kannst du ja locker beieinanderlassen.
Du könntest sogar anfangen, zum Beispiel für 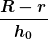 eine Abkürzung einzuführen, weil das so oft vorkommt. Zum Beispiel eine Abkürzung einzuführen, weil das so oft vorkommt. Zum Beispiel 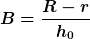 . .
Magst du das mal probieren und versuchen, ob dein monsterlanger Gesamtterm dadurch auf eine viel überschaubarere und leichter handhabbare Größe zusammenschrumpft?
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 18:56 Titel: Sonex Verfasst am: 10. Dez 2008 18:56 Titel: |
 |
|
Also was du mit R-1/ho meinst weiß ich jetzt ganz und gar nicht
wo soll denn das sein
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Dez 2008 19:02 Titel: dermarkus Verfasst am: 10. Dez 2008 19:02 Titel: |
 |
|
Damit meine ich: Wenn du deine Gleichung ganz am Anfang als
^2\cdot \pi}{r^2 \pi \cdot \sqrt{2gh}}\right) \, \dd h)
schreibst, indem du ein paar Konstanten zu der Konstanten 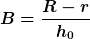 zusammenfasst (oder alternativ den Term zusammenfasst (oder alternativ den Term 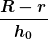 beim Umformen einfach immer ganz lässt), dann sparst du dir viel Arbeit beim Schreiben und Umformen, und deine Rechnung wird nochmal viel, viel übersichtlicher. beim Umformen einfach immer ganz lässt), dann sparst du dir viel Arbeit beim Schreiben und Umformen, und deine Rechnung wird nochmal viel, viel übersichtlicher.
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 19:27 Titel: Sonex Verfasst am: 10. Dez 2008 19:27 Titel: |
 |
|
(R-r)]^2 h^{-\frac{1}{2}}(t)dh(t))
^2=r^2+2bhr+b^2 h^2)
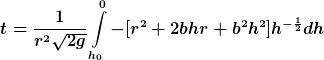
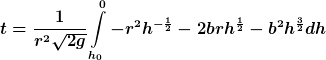
na das sieht schon mal toll aus.. und auch richtig so?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Dez 2008 19:31 Titel: dermarkus Verfasst am: 10. Dez 2008 19:31 Titel: |
 |
|
Einverstanden, nur weiter so 
Wie ich sehe, hast du stillschweigend gleich noch eine weitere neue Konstante eingeführt und sie b=B genannt, stimmts?  (Achte bei Variablenbuchstaben auf Groß- und Kleinschreibung, oft verwendet man das zur Unterscheidung unterschiedlicher Variablen) (Achte bei Variablenbuchstaben auf Groß- und Kleinschreibung, oft verwendet man das zur Unterscheidung unterschiedlicher Variablen)
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 19:48 Titel: Sonex Verfasst am: 10. Dez 2008 19:48 Titel: |
 |
|
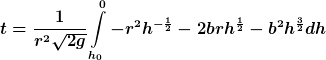
|_{h_{o}}^{0})
)
Die wichtigsten Schritte habe ich hingeschrieben... nun wäre ja nur noch b zu ersetzen
b=B
)
schon mal vorgerechnet t=0,55s
Zuletzt bearbeitet von Sonex am 10. Dez 2008 19:59, insgesamt einmal bearbeitet |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Dez 2008 19:57 Titel: dermarkus Verfasst am: 10. Dez 2008 19:57 Titel: |
 |
|
Einverstanden, da hast du ein paar richtige Bruchstücke dieser Rechnung hingeschrieben.
Magst du nun wieder darauf aufpassen, dass du die Gleichheitszeichen, Vorfaktoren, ... alle wieder mit dazuschreibst, und damit bis zur Endergebnis-Formel für t weiterrechnen?
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 20:05 Titel: Sonex Verfasst am: 10. Dez 2008 20:05 Titel: |
 |
|
}{r^2 \sqrt{2g}})
^2h_{o}^{\frac{5}{2}}+20(\frac{R-r}{h_{o}})rh_{0}^{\frac{3}{2}}+30r^2h_{0}^{\frac{1}{2}}}{15})}{r^2 \sqrt{2g}})
^2*10^{\frac{5}{2}}+20(\frac{5-0,25}{10})*0,25*10^{\frac{3}{2}}+30*0,25^2*10^{\frac{1}{2}}}{15})}{0,25^2 \sqrt{2*981}})
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 20:09 Titel: Sonex Verfasst am: 10. Dez 2008 20:09 Titel: |
 |
|
|
t=1,77 ???
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Dez 2008 20:33 Titel: dermarkus Verfasst am: 10. Dez 2008 20:33 Titel: |
 |
|
Magst du am besten deine Endergebnis-Formel erst noch fertig ausrechnen, bevor du die ganzen Zahlenwerte einsetzt? Du kannst deine Formel noch viel übersichtlicher schreiben, indem du zum Beispiel das h_0 noch ein bisschen kürzt und ein bisschen was passend ausklammerst.
Dann wird das, was du am Ende noch einsetzen und eintippen musst, so kurz, dass es viel weniger wahrscheinlich wird, dass du dich am Ende noch irgendwo im Taschenrechner vertippst. 
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 21:00 Titel: Sonex Verfasst am: 10. Dez 2008 21:00 Titel: |
 |
|
^2h_{o}^{\frac{5}{2}}+20(\frac{R-r}{h_{o}})rh_{0}^{\frac{3}{2}}+30r^2h_{0}^{\frac{1}{2}}}{15})}{r^2 \sqrt{2g}})
^2h_{o}^{\frac{3}{2}}+20(R-r)rh_{0}^{\frac{1}{2}}+30r^2h_{0}^{\frac{1}{2}}}{15})}{r^2 \sqrt{2g}})
so würd ich es dann lassen... richtig so
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Dez 2008 21:04 Titel: dermarkus Verfasst am: 10. Dez 2008 21:04 Titel: |
 |
|
Links oben ist noch ein Fehler drin.
Siehst du danach dann, was du noch ausklammern könntest, um dir noch mehr Eintipparbeit zu ersparen?
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 21:19 Titel: Sonex Verfasst am: 10. Dez 2008 21:19 Titel: |
 |
|
|
Wenn ich wüsste welches der Fehler wer... gewiss
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Dez 2008 21:29 Titel: dermarkus Verfasst am: 10. Dez 2008 21:29 Titel: |
 |
|
Mögliche Prüfmethoden zum Finden von Fehlern:
* Passen die Einheiten der jeweiligen Terme zueinander, oder sticht zum Beispiel ein Term heraus, so dass Äpfel mit Birnen addiert würden?
* Hast du beim Rechnen alle Klammern und alle Quadrate daran berücksichtigt?
* Welche Rechenschritte hast du zwischen diesen beiden Zeilen gemacht, und kannst du sie alle nochmal genau kontrollieren?
|
|
 |
wishmoep
Anmeldungsdatum: 07.09.2008
Beiträge: 1342
Wohnort: Düren, NRW
|
 wishmoep Verfasst am: 10. Dez 2008 21:34 Titel: wishmoep Verfasst am: 10. Dez 2008 21:34 Titel: |
 |
|
Noch ein Zusatz zu deinen "Testmethoden" dermarkus:
Die Stammfunktion einmal ableiten und schauen, ob das gleiche wie hinter dem Integralzeichen herauskommt. 
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 21:42 Titel: Sonex Verfasst am: 10. Dez 2008 21:42 Titel: |
 |
|
^2h_{o}^{\frac{1}{2}}+20(R-r)rh_{0}^{\frac{1}{2}}+30r^2h_{0}^{\frac{1}{2}}}{15})}{r^2 \sqrt{2g}})
^2+20(R-r)r+30r^2}{15})}{r^2 \sqrt{2g}})
na ist das nicht schon besser
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Dez 2008 21:46 Titel: dermarkus Verfasst am: 10. Dez 2008 21:46 Titel: |
 |
|
deutlich besser 
Wenn du jetzt noch Lust hast, könntest du den ganzen Bruch noch mit r^2 kürzen, dann hast du alle r's und R's immer nur noch in Form von  drinstehen. drinstehen.
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 21:50 Titel: Sonex Verfasst am: 10. Dez 2008 21:50 Titel: |
 |
|
}{ \sqrt{2g}})
hier... 
t=2,5 s
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. Dez 2008 22:01 Titel: dermarkus Verfasst am: 10. Dez 2008 22:01 Titel: |
 |
|
Du hast es so ein bisschen mit den Quadraten links oben, stimmts? Da ist noch so ein Fehler passiert.
Die Wurzeln würde ich übrigens alle nach vorne vor den Bruch schreiben, und die Zahlenbrüche einfach noch kürzen, dann hat man nur noch ganz einfache, übersichtliche Terme in der Endformel drinstehen. 
|
|
 |
Sonex
Anmeldungsdatum: 30.10.2008
Beiträge: 120
Wohnort: Magdeburg
|
 Sonex Verfasst am: 10. Dez 2008 22:13 Titel: Sonex Verfasst am: 10. Dez 2008 22:13 Titel: |
 |
|
^2}{15 r^2}+\frac{4(R-r)}{3r}+2))
nun 
dann bekomme ich qwas mit 12 raus....
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 11. Dez 2008 04:10 Titel: dermarkus Verfasst am: 11. Dez 2008 04:10 Titel: |
 |
|
| Sonex hat Folgendes geschrieben: |
dann bekomme ich qwas mit 12 raus.... |
Das wäre ja dann deutlich größer als die meisten deiner bisherigen genannten Werte für t.
Kann dieser Wert für t einigermaßen stimmen?
Magst du zum Beispiel mal mit einer groben und vereinfachten Näherungsrechnung überprüfen, ob dieses Ergebnis nun größenordnungsmäßig Sinn macht?
So ganz ungefähr ist ja das  \approx \frac{h}{h_0}\cdot R) , wenn man den Unterschied durch die Kegelspitze untendran mal einfach vernachlässigt. Wenn du mit diesem vereinfachten r(h) die ganze Rechnung mal durchziehst, dann sollte das zum einen deutlich einfacher gehen als die exaktere Variante (weil die Gleichung, mit der man anfängt, mit dieser Näherung viel einfacher wird), aber zum anderen sollte zumindest grob ungefähr dasselbe für die Zeit t herauskommen. , wenn man den Unterschied durch die Kegelspitze untendran mal einfach vernachlässigt. Wenn du mit diesem vereinfachten r(h) die ganze Rechnung mal durchziehst, dann sollte das zum einen deutlich einfacher gehen als die exaktere Variante (weil die Gleichung, mit der man anfängt, mit dieser Näherung viel einfacher wird), aber zum anderen sollte zumindest grob ungefähr dasselbe für die Zeit t herauskommen.
|
|
 |
|
















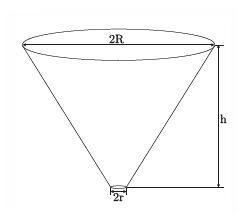
 Hoppla, was soll denn das??
Hoppla, was soll denn das?? 
 (Achte bei Variablenbuchstaben auf Groß- und Kleinschreibung, oft verwendet man das zur Unterscheidung unterschiedlicher Variablen)
(Achte bei Variablenbuchstaben auf Groß- und Kleinschreibung, oft verwendet man das zur Unterscheidung unterschiedlicher Variablen)