| Autor |
Nachricht |
handy33
Gast
|
 handy33 Verfasst am: 13. Jun 2011 20:07 Titel: Kreisbewegung einer Kugel im Kegel handy33 Verfasst am: 13. Jun 2011 20:07 Titel: Kreisbewegung einer Kugel im Kegel |
 |
|
Hallo, ich bin verzweifelt 
In einem auf die Spitze gestellten Kegel mit dem Öffnungswinkel a soll eine Kugel rotieren, sodass sie konstant auf einer Höhe bleibt.
A) Zeichnen Sie die auf die KUgel wirkenden Beschleunigungen in die Skizze ein. Stellen Sie die Gleichung auf, die die notwendige Radialbeschleunigung in Abhängigkeit vom Öffnungswinkel a des Kegels und der Höhe h oberhalb der Kegelspitze angibt.
B) Bestimmen Sie die Umlaufzeit der Kugel in Abhängigkeit vom Öffnungswinkel a des Kegels und der Höhe h oberhalb der Kegelspitze.
c) Mit welcher Kraft drückt die Kugel auf die Kegelmantelfläche??
d) berechnen sie die Umlaufzeit aus B) und die Kraft aus c) mit den Beispielwerten a= 45°, m= 200 g und h=30cm. Welche umlaufgeschwindigkeit hat die Kugel??
Meine Ideen:
b) tan(alpha)=F(z)/F(G) --> F(z)=F(G)*tan(alpha)
einsetzen: (4*pi^2*m*r)/T^2 = m*g*tan(alpha)
macht: T^2= (4*pi^2*r)/(g*tan(alpha))
a) wieder F(z)=F(G)*tan(alpha)
= (mv^2)/r = m*g*tan(alpha)
v^2=r*g*tan(alpha)
da es eine Kegel ist --> Dreieck einzeichnen: der halbe tan(alpha)=h/r
also Höhe/ Radius
dann ist: v=halber tan(alpha)*h*g*tan(alpha)
Ist das richtig so?
c) F=Wurzel aus: Fz^2 + F(G)^2
Ist das korrekt so?
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 13. Jun 2011 21:27 Titel: franz Verfasst am: 13. Jun 2011 21:27 Titel: |
 |
|
Handelt es sich wirklich um eine rotierende Kugel (dazu reicht das Wort "Kugel" alleine nicht) oder um einen sich im Kegel bewegenden Punkt?
[Vielleicht auch mal Suchfunktion bemühen.]
|
|
 |
handy33
Gast
|
 handy33 Verfasst am: 13. Jun 2011 21:51 Titel: handy33 Verfasst am: 13. Jun 2011 21:51 Titel: |
 |
|
|
Der Titel lautet: Rotation im Kegel....was meinst du? Ich weiß nicht genau...ich gehe von einem Punkt aus...oder bin die ganze Zeit von ausgegangen...
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
|
 |
handy33
Gast
|
 handy33 Verfasst am: 13. Jun 2011 22:54 Titel: handy33 Verfasst am: 13. Jun 2011 22:54 Titel: |
 |
|
Das hatte ich schon gesehen, aber das hatten wir alles noch nicht...auch keine Energie und sonst was. Ich bin erst in der 10. also darf das auch nichts kompliziertes mit irgendwelchen über drei Zeilen geschweiften Klammern gehen...
Ich habe doch schon eine Idee geschrieben...ist das so richtig? Also angenommen die Kugel rotiert nicht um sich selbst, sondern ist ein Punkt...denn Rotation hatten wir noch nicht...
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 13. Jun 2011 23:14 Titel: VeryApe Verfasst am: 13. Jun 2011 23:14 Titel: |
 |
|
| Franz hat Folgendes geschrieben: |
Handelt es sich wirklich um eine rotierende Kugel (dazu reicht das Wort "Kugel" alleine nicht) oder um einen sich im Kegel bewegenden Punkt?
|
was wäre denn deiner Meinung nach bei einer rotierenden Kugel anders?
|
|
 |
handy33
Gast
|
 handy33 Verfasst am: 13. Jun 2011 23:23 Titel: handy33 Verfasst am: 13. Jun 2011 23:23 Titel: |
 |
|
Weiß ich nicht...also eigentlich wäre nichts anders! Aber franz verwirrt mich 
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 13. Jun 2011 23:34 Titel: VeryApe Verfasst am: 13. Jun 2011 23:34 Titel: |
 |
|
ohne Reibung müsstest du nur berücksichtigen das der Schwerpunkt der Kugel nicht mehr auf der Kegeloberfläche liegt, wie bei einer Punktmasse, denn die Kugel hat eine Raumausdehnung.
| Zitat: |
da es eine Kegel ist --> Dreieck einzeichnen: der halbe tan(alpha)=h/r
also Höhe/ Radius
dann ist: v=halber tan(alpha)*h*g*tan(alpha)
Ist das richtig so?
c) F=Wurzel aus: Fz^2 + F(G)^2
Ist das korrekt so?
|
kannsd du das erläutern.
halber tan alpha und was du dann weiter machst.
|
|
 |
handy33
Gast
|
 handy33 Verfasst am: 14. Jun 2011 13:47 Titel: handy33 Verfasst am: 14. Jun 2011 13:47 Titel: |
 |
|
Ja, also wir gehen dann mal von einem Punkt aus. Also bisher sind wir immer von einem Punkt ausgegangen, bei dieser Aufgabe dann wohl auch 
| Zitat: | a) wieder F(z)=F(G)*tan(alpha)
= (mv^2)/r = m*g*tan(alpha)
v^2=r*g*tan(alpha)
da es eine Kegel ist --> Dreieck einzeichnen: der halbe tan(alpha)=r/h
also Höhe/ Radius
dann ist: v=halber tan(alpha)*h*g*tan(alpha) |
Da habe ich in v^2=r*g*tan(alpha) das r ersetzt durch r= halber tan(alpha)*h
Mein Neuer Ansatz:
halbnr tan(alpha)=Fz/F(g)
und halber tan (alpha)=r/h
das dann gleichgesetzt:
(m*v^2/r) / (m*g) = r/h
macht: v^2=r^2*g*h
oder: v^2/r = halber tan(alpha)*h*g / h
h kürzt sich weg: v^2/r = halber tan(alpha)*g
Oder so? Oder alles falsch? Wie geht denn jetzt die a)?
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 14. Jun 2011 14:30 Titel: VeryApe Verfasst am: 14. Jun 2011 14:30 Titel: |
 |
|
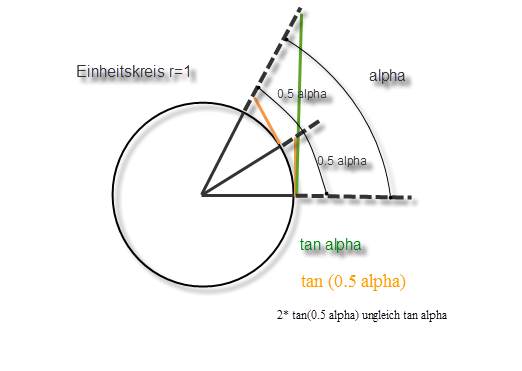
das mit den winkeln nochmals überdenken.
| Beschreibung: |
|
| Dateigröße: |
40.92 KB |
| Angeschaut: |
4375 mal |
|
|
|
 |
handy33
Gast
|
 handy33 Verfasst am: 14. Jun 2011 14:44 Titel: handy33 Verfasst am: 14. Jun 2011 14:44 Titel: |
 |
|
Aber ist das nicht so:
www (und dann). brecht-oberschule.de/geo/kegel/bilder/kegel.gif (ein Bild vom Kegel)
Also der Winkel alpha zwischen h und s
h ist auch gleich Fg und r gleich F(z) oder?
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 14. Jun 2011 15:12 Titel: VeryApe Verfasst am: 14. Jun 2011 15:12 Titel: |
 |
|
alpha bezeichnet bei dir doch den Öffnungswinkel.
)
)
 ungleich \frac {tan(\alpha)}{2} )
siehe skizze oben
|
|
 |
handy33
Gast
|
 handy33 Verfasst am: 14. Jun 2011 15:49 Titel: handy33 Verfasst am: 14. Jun 2011 15:49 Titel: |
 |
|
Ach das meinst du...ne ich meinte schon tan(0,5alpha) ----> also, dass wenn der Winkel voll z.B. 60° ist... der dann nur noch 30° ist...also der halbe Kegelwinkel, damit man ein Dreieck hat...
Was hast du den als Formel für a) raus? Dann kann ich ja einfach gucken, dass ich mal probiere, ob ich die auch herleiten kann...nur ich weiß von meinen mitlerweile ca. 30 Formeln nicht, welche stimmt...und das sollte ich, wenn ich Freitag darüber ne Klausur schreibe 
|
|
 |
Packo
Gast
|
 Packo Verfasst am: 14. Jun 2011 15:57 Titel: Packo Verfasst am: 14. Jun 2011 15:57 Titel: |
 |
|
handy,
und warum schreibst du halber tan(alpha) wenn du tan(halber Winkel) meinst???
|
|
 |
handy33
Gast
|
 handy33 Verfasst am: 14. Jun 2011 16:02 Titel: handy33 Verfasst am: 14. Jun 2011 16:02 Titel: |
 |
|
Weil ich dachte, dass man so besser versteht, was ich meine...ebend von z.B. 60° die Hälfte...
Stimmt denn dann irgendwas von den Formeln?
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 15. Jun 2011 18:38 Titel: franz Verfasst am: 15. Jun 2011 18:38 Titel: |
 |
|
Meine Frage oben bezüglich der Kugel bitte ignorieren; das ist eine andere Liga. Es bleibt bei Kullerchen / Punkten.
Skizze liegt sicher vor; Winkelbeziehung (wie angegeben) überprüfen. Dann noch der Zusammenhang Höhe / Radius. Und damit eventuell die Rollzeit T - abhängig von alpha und h bestimmen.
|
|
 |
handy33
Gast
|
 handy33 Verfasst am: 15. Jun 2011 21:20 Titel: handy33 Verfasst am: 15. Jun 2011 21:20 Titel: |
 |
|
So, ich hab jetzt raus:
a) v^2/r = tan(0,5alpha)*g
b)T^2=(4*pi^2*h) / g
c) Fn= Wurzel aus Fz^2 + F(g)^2
Hab langsam keine Lust mehr...was ist denn jetzt die Lösung?
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 15. Jun 2011 22:03 Titel: franz Verfasst am: 15. Jun 2011 22:03 Titel: |
 |
|
|
Mir scheint, daß mit den Winkelbeziehungen zwischen den Kräften etwas noch nicht stimmt. Bei mir G / Z = tan alpha/2 usw.
|
|
 |
handy33
Gast
|
 handy33 Verfasst am: 15. Jun 2011 22:17 Titel: handy33 Verfasst am: 15. Jun 2011 22:17 Titel: |
 |
|
Was stimmt denn nicht? Ich wollte ja keine fertige Lösung, aber die Zeit drängt bis Freitag und ich hab mein Bestes versucht 
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 15. Jun 2011 22:21 Titel: franz Verfasst am: 15. Jun 2011 22:21 Titel: |
 |
|
|
Hast Du inzwischen eine Skizze: Kegel mit Kuller und die dort angreifenden Krafte? Insbesondere das Verhältnis F_G : F_Z?
|
|
 |
handy33
Gast
|
 handy33 Verfasst am: 15. Jun 2011 22:24 Titel: handy33 Verfasst am: 15. Jun 2011 22:24 Titel: |
 |
|
Ja:
Fg nach unten, Fz nach innen, Fn auf die Fläche, dabei ist Fz die resultierende Kraft...
|
|
 |
handy33
Gast
|
 handy33 Verfasst am: 15. Jun 2011 22:32 Titel: handy33 Verfasst am: 15. Jun 2011 22:32 Titel: |
 |
|
|
Oder ist tan(alpha)= Fg/Fz??? Also, wenn ich das mal so anders einzeichne....
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 15. Jun 2011 22:42 Titel: franz Verfasst am: 15. Jun 2011 22:42 Titel: |
 |
|
Jetzt dämmert es mir, Du hast die Zentripetalkraft nach innen gezeichnet. Dann mußt Du das Gewicht zerlegen nach Zentripetalkraft und Normalkraft.
Einfacher wird es vermutlich, wenn Du die Zentrifugalkraft (nach außen) malst und senkrecht zur Wand die Normalkraft, welche sich aus F_Z und F_G ergibt.
So oder so, betragsmäßig F_G : F_Z = tan alpha/2
alpha ist der gesamte Öffnungswinkel des Kegels; der Neigungswinkel des Kegelmantels alpha/2.
|
|
 |
handy33
Gast
|
 handy33 Verfasst am: 15. Jun 2011 23:01 Titel: handy33 Verfasst am: 15. Jun 2011 23:01 Titel: |
 |
|
Also wenn gilt:
tan(0,5alpha)=Fg/Fz
tan(0,5alpha)=r/h
gleichsetzen:
g*h/r=v^2/r
und das r links ersetzen durch h*tan(0,5alpha)
g/tan(0,5alpha)=v^2/r
Aber man kann nie, wie in a) gefordert, die Zentripetalbeschleunigung in Abhängigkeit von Höhe UND Winkel angeben...oder ist immer noch was falsch?
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 15. Jun 2011 23:43 Titel: franz Verfasst am: 15. Jun 2011 23:43 Titel: |
 |
|
|
Du hast doch die Zentripetalbeschleunigung v^2/r. Was willst Du mehr?
|
|
 |
|



















