| Autor |
Nachricht |
Veryyy
Anmeldungsdatum: 14.08.2009
Beiträge: 142
|
 Veryyy Verfasst am: 20. Okt 2009 17:11 Titel: Welche Kugel kommt schneller unten an? Veryyy Verfasst am: 20. Okt 2009 17:11 Titel: Welche Kugel kommt schneller unten an? |
 |
|
Hallo,
ich bin auf die Frage gestoßen, welche von zwei Kugeln schneller unten ankommt.
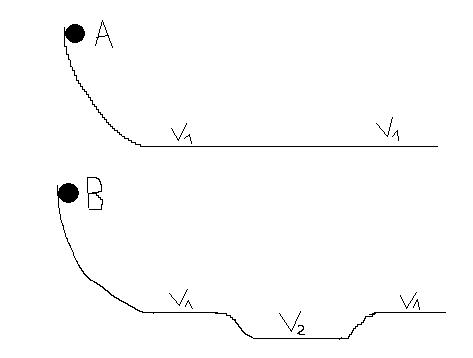
Ich habe einmal eine Skizze angehängt.
Also es rollen Kugel A und Kugel B genau denselben Abhang hinunter. Währenddessen läuft die Zeit. Sie wird genau dann gestoppt, wenn die Kugel den rechten Rand der Zeichunung erreicht hat. Jetzt ist die Frage, welche von beiden Kugeln schneller rechts ankommt. Reibung soll vernachlässigt werden.
Meine Überlegungen dazu:
1. Wenn die Kugeln die ebene Fläche erreichen, haben sie die gleiche Geschwindigkeit 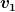 . Kugel B hat in der Kuhle noch eine höhere Geschwindigkeit . Kugel B hat in der Kuhle noch eine höhere Geschwindigkeit 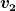 und wenn sie wieder oben ist wieder die Geschwindigkeit und wenn sie wieder oben ist wieder die Geschwindigkeit 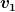 , weil die Geschwindigkeit, die Kugel B durch das Hinabrolle in die "Wanne" gewonnen hat, - also , weil die Geschwindigkeit, die Kugel B durch das Hinabrolle in die "Wanne" gewonnen hat, - also  beim Hinaufrollen aufgrund des Energieerhaltungssatzes ja genau verloren geht. beim Hinaufrollen aufgrund des Energieerhaltungssatzes ja genau verloren geht.
Dies ist ja ein Argument dafür, dass Kugel B schneller am Ende ankommt.
2. Kugel B hat einen längeren Weg zurückzulegen. Sie hat ja durch das Hinab- und Hinaufrollen zusätzliche Wegstrecke.
Dies ist ein Argument dafür, dass Kugel A schneller am Ende ankommt.
3. Beide Effekte heben sich genau auf. Beide Kugeln kommen gleichzeitig am Ende an.
Was meint ihr?
Gruß,
Veryyy
| Beschreibung: |
|
| Dateigröße: |
9.05 KB |
| Angeschaut: |
11415 mal |
|
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 20. Okt 2009 19:38 Titel: TomS Verfasst am: 20. Okt 2009 19:38 Titel: |
 |
|
Ausrechnen!
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 20. Okt 2009 19:42 Titel: franz Verfasst am: 20. Okt 2009 19:42 Titel: |
 |
|
Kein Gefühl dafür.
Primitives Modell: Symmetrisch hangab und hangauf. Müßte, nach flüchtiger Rechnung, länger dauern aus geradeaus...
|
|
 |
Veryyy
Anmeldungsdatum: 14.08.2009
Beiträge: 142
|
 Veryyy Verfasst am: 20. Okt 2009 19:53 Titel: Veryyy Verfasst am: 20. Okt 2009 19:53 Titel: |
 |
|
Also das war eher eine theoretische Frage. Wir sollten eben durch Überlegen und nicht durch Rechnen auf eine Lösung kommen.
Aber wenn du schon das Stichwort Ausrechnen gibst, würde ich den Energieerhaltungssatz anwenden:

Am Anfang steckt alles in der potentiellen Energie. Am Ende wurde diese in kinetische Energie umgewandelt. Reibungsenergie und Rotationsenergie sollen einmal vernachlässigt werden.
Demnach müsste die Geschwindigkeit von beiden Kugeln am Ende ja gleich groß sein... (so könnte man es ja allgemein ausrechnen). Hier wird allerdings nur die Endgeschwindigkeit berechnet. Die Geschwindigkeit in der Kuhle muss man dann noch einzeln berechnen und kommt logischerweise auf eine größere. Dann berechne ich die Strecke und dann mit  die Zeit. die Zeit.
Anschaulich tendiere ich aber gerade eher dazu, dass die Kugel B schneller ist, bzw kürzer braucht, um das Ziel zu erreichen. Sie ist ja in einem Stück zwischendrin schneller.
Wenn ich mir dieses Stück nun ziemlich groß vorstelle, wird der Verlust durch die Strecke, die die Kugel zusätzlich zurücklegt, vernachlässigbar klein. Und so müsste die Kugel B schneller unten sein...
Also sage ich: Kugel B ist (auf jeden Fall für lange Kuhlen) schneller.
Bei kurzen Kuhlen wird wohl die zusätzliche Strecke mehr ausmachen, als die schnellere Geschwindigkeit (da diese ja nur sehr kurz wirkt, die Verlängerung der Strecke aber gleich groß ist)
Da ist dann Kugel A schneller.
@franz, ja das stimmt, aber ich habe bei einer langen Kuhle ja auch eine größere Geschwindigkeit, für die Zeit in der die Kugel in der Kuhle rollt.
Also hängt die Lösung von der Länge der Kuhle ab?
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 20. Okt 2009 20:02 Titel: franz Verfasst am: 20. Okt 2009 20:02 Titel: |
 |
|
| Veryyy hat Folgendes geschrieben: | | Also hängt die Lösung von der Länge der Kuhle ab? |
Bei meinem schlichten und unrealen "Modell" (der Körper läuft zum Beispiel keinen Knick) ist das Verhältnis der Zeiten von v und der Hanggeometrie abhängig).
PS Mit "Gefühlsphysik" kann ich nicht dienen.
|
|
 |
Veryyy
Anmeldungsdatum: 14.08.2009
Beiträge: 142
|
 Veryyy Verfasst am: 20. Okt 2009 20:45 Titel: Veryyy Verfasst am: 20. Okt 2009 20:45 Titel: |
 |
|
Ich habe ein Video dazu gefunden, was fast den gleichen Sachverhalt behandelt:
http://193.196.151.150/physikonline/video1/m2_dynamik/bahnrennen1.html
Also ist es auf jeden Fall möglich, dass Kugel B schneller ist.
Kostet die Strecke die Kugel B zusätzlich rollt, aber wirklich Zeit? Ich glaube nicht, da ich es mit einer Überlagerung von Bewegungen vergleiche. Ein Ball der fallengelassen wird, erreicht gleichzeitig den Boden, wie ein Ball der senkrecht geworfen wird.
Ein Ball der waagerecht rollt wird gleichzeitig eine senkrechte Gerade passieren, wie ein Ball der mit der gleichen Geschwindigkeit waagrecht geworfen wird. Die Bewegung nach unten beeinflusst die Bewegung nach rechts nicht.
Kugel B wird also wenn man die "Kuhle gegen 0 gehen lässt" (einmal mathematisch geschrieben) immer kürzer vor Kugel A am Ziel ankommen, da sie immer kürzer die hörere Geschwindigkeit in der Kuhle hat. Sie wird aber immer schneller sein..
Stimmt ihr mir da zu?
| Zitat: | | Bei meinem schlichten und unrealen "Modell" (der Körper läuft zum Beispiel keinen Knick) ist das Verhältnis der Zeiten von v und der Hanggeometrie abhängig). |
ja, ich gehe auch davon aus, dass die Zeiten selbst stark von der Hanggeometrie abhängen. Und man muss ja stets mit Vereinfachungen arbeiten. Aber eigentlich müsste B immer schneller sein...
|
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 20. Okt 2009 20:54 Titel: para Verfasst am: 20. Okt 2009 20:54 Titel: |
 |
|
Randnotiz: mit der schnellsten (nicht kürzesten) Verbindung zwischen zwei Punkten beschäftigt sich das Problem der Brachistochrone.
_________________
Formeln mit LaTeX |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 20. Okt 2009 23:28 Titel: TomS Verfasst am: 20. Okt 2009 23:28 Titel: |
 |
|
Der Tip von para ist gut.
In dem hier vorliegenden einfachen Fall würde ich mir zunächst mal den Grenzfall unendlich steiler Kuhlen anschauen, also den Fall, dass die Geschwindigkeit instantan am Rand der Kuhle einen Sprung macht; dann sollte das ja mit dem Weg-Zeit-Gesetz einfach lösbar sein, oder?
Gruß
Tom
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Veryyy
Anmeldungsdatum: 14.08.2009
Beiträge: 142
|
 Veryyy Verfasst am: 21. Okt 2009 17:02 Titel: Veryyy Verfasst am: 21. Okt 2009 17:02 Titel: |
 |
|
Danke für die Tipps. Ich habe mir das mit der Brachistochrone jetzt mal angeschaut.
| Zitat: | | In dem hier vorliegenden einfachen Fall würde ich mir zunächst mal den Grenzfall unendlich steiler Kuhlen anschauen, also den Fall, dass die Geschwindigkeit instantan am Rand der Kuhle einen Sprung macht; dann sollte das ja mit dem Weg-Zeit-Gesetz einfach lösbar sein, oder |
Wenn man diesen Grenzfall betrachtet, ist ganz klar, dass die Kugel B schneller am Ziel. Sie ist ja immer entweder gleichschnell wie A oder schneller (in der Kuhle- egal wie kurz oder lang diese ist).
Ich habe mir jetzt noch überlegt, dass Kugel B immer schneller ankommen muss, weil es sich um eine Überlagerung von Bewegungen handelt. Die Horizontalgeschwindigkeit die immer 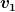 ist, wird auf dem Weg in die Kuhle verstärkt (die Kugel wird schneller) auf dem Weg aus der Kuhle abgeschwächt (die Kugel wird wieder auf ist, wird auf dem Weg in die Kuhle verstärkt (die Kugel wird schneller) auf dem Weg aus der Kuhle abgeschwächt (die Kugel wird wieder auf 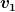 abgebremst. abgebremst.
Auch während die Kugel sich auf dem Weg in die Kuhle befindet (also an dem ganz kleinen Stück an dem es runter geht, wenn man jetzt einmal nicht den Grenzfall betrachet) bewegt sie sich ja genau so schnell nach rechts weiter. Durch das Hinabrollen wird diese Bewegung noch durch eine zusätzliche Beschleunigungsbewegung überlagert. Und damit rollt die Kugel noch schneller. Diese zusätzliche Beschleunigungsbewegung wird am Ende der Kuhle ganau wieder aufgehoben. Wieder durch Überlagerung sodass wieder genau die horizontale Geschwindigkeit erreicht wird.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 21. Okt 2009 17:31 Titel: TomS Verfasst am: 21. Okt 2009 17:31 Titel: |
 |
|
Mal ein paar Formeln dazu:
Zunächst mal die Laufzeit der Kugel in Abhängigkeit von der Geschwindigkeit:
})
Dann der Fall stückweise flacher Strecken mit konstanter Geschwindigkeit

Dann der Vergleich der beiden Kurven bzw. Zeiten im o.g. Fall

)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 21. Okt 2009 23:26, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 21. Okt 2009 17:57 Titel: TomS Verfasst am: 21. Okt 2009 17:57 Titel: |
 |
|
Außerdem kann man natürlich noch das Profil der Kurve einbringen:


Dabei ist h eine Funktion h(s).
Allerdings benötigt man zum Rechnen eine Funktion h(x), d.h. man muss zunächst s=s(x) über die Bogenlänge der Kurve bestimmen und im Integral dann substituieren:
 = \sqrt{\frac{2E_0}{m} - 2gh(x)})
}{v(s(x))} = \int_0^X dx \frac{s^\prime(x)}{\sqrt{\frac{2E_0}{m} - 2gh(x)}})
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
 Gajeryis Verfasst am: 21. Okt 2009 18:55 Titel: Gajeryis Verfasst am: 21. Okt 2009 18:55 Titel: |
 |
|
Glaub mir, du willst diese Aufgabe nicht analytisch lösen.  Ich habe seit Eröffnung des Threads mehrere A4 Seiten vollgekritzelt, im Versuch, die Brachistochrone herzuleiten bzw. die Laufzeit anderer Kurven zu rechnen. Die Herleitung der Brachistochrone auf Wikipedia kapiere ich mittlerweile, aber wie sie auf den parametrisierten Ansatz gekommen sind, entfällt jeglicher Erkenntnis meinerseits. Aber ich bin auch kein Mathematiker. Ich habe seit Eröffnung des Threads mehrere A4 Seiten vollgekritzelt, im Versuch, die Brachistochrone herzuleiten bzw. die Laufzeit anderer Kurven zu rechnen. Die Herleitung der Brachistochrone auf Wikipedia kapiere ich mittlerweile, aber wie sie auf den parametrisierten Ansatz gekommen sind, entfällt jeglicher Erkenntnis meinerseits. Aber ich bin auch kein Mathematiker.
Ich ergänze mal noch deine Formeln:
}ds = \int_{0}^{\hat{x}} \frac{1}{v(x)} \sqrt{1+h'(x)^{2}}dx \quad \rm{wobei} \quad h'(x) = \frac{\partial}{\partial x}h(x))
mit v = v(h)
^{2}} { \frac{2 \cdot E_{0}} {m} - 2gh(x)} } dx)
Schon mit einer Funktion h(x) in der Form einer Parabel oder eine Katenoide gibt es äusserst mühsame Integrale, bei welchen sogar der Wolfram Online Integrator seine Zeit braucht - wenn er denn eine halbwegs anwendbare Lösung ausspuckt.
Geradenstücke sind ohne Integral einfacher zu lösen.

|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 21. Okt 2009 20:23 Titel: TomS Verfasst am: 21. Okt 2009 20:23 Titel: |
 |
|
Dass sich eklige Integrale ergeben, ist klar. Aber Mathematica sollte das schon schaffen ... Mir ging es aber eher darum, den allgemeinen Zusammenhang darzustellen.
Die Geradenstücke sind jedenfalls der logisch nächste Schritt zu meiner o.g. sehr vereinfachten Formel. Mal sehen, ob mir dazu noch was einfällt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 21. Okt 2009 21:32 Titel: TomS Verfasst am: 21. Okt 2009 21:32 Titel: |
 |
|
Ach übrigens; die ursprüngliche Aufgabe ist natürlich schon gelöst ...
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Veryyy
Anmeldungsdatum: 14.08.2009
Beiträge: 142
|
 Veryyy Verfasst am: 21. Okt 2009 22:37 Titel: Veryyy Verfasst am: 21. Okt 2009 22:37 Titel: |
 |
|
uiuiui, also bei den komplizierten Formeln bin ich ausgestiegen.
| Zitat: | | Ach übrigens; die ursprüngliche Aufgabe ist natürlich schon gelöst ... |
Nur nochmals um sicherzugehen. Die richtige Lösung ist: Kugel B kommt schneller unten an, oder?
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 21. Okt 2009 22:57 Titel: TomS Verfasst am: 21. Okt 2009 22:57 Titel: |
 |
|
Der Vergleich der beiden Kurven bzw. Zeiten im o.g. Fall

)
reicht völlig aus.
Man sieht, dass im zweiten Fall ein Teil der Bahn mit einer größeren Geschwindigkeit durchlaufen wird. Damit ist die benötigte Zeit aber kürzer. Da die Skizze sehr ungenau ist, kannst du ohne exakte Angabe der Kurve ja eh nur qualitativ argumentieren.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 21. Okt 2009 23:27, insgesamt einmal bearbeitet |
|
 |
Veryyy
Anmeldungsdatum: 14.08.2009
Beiträge: 142
|
 Veryyy Verfasst am: 21. Okt 2009 23:09 Titel: Veryyy Verfasst am: 21. Okt 2009 23:09 Titel: |
 |
|
Also die Rechnung habe ich soweit nachvollzogen. Direkt nach dem letzten Gleichheitszeichen müsste  statt statt 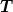 stehen, oder? Du ersetzt ja gerade stehen, oder? Du ersetzt ja gerade  durch durch 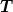 . .
Das heißt ich ziehe von der Zeit  die die obere Kugel braucht noch etwas ab, die untere Kugel muss also schneller am Ziel sein. die die obere Kugel braucht noch etwas ab, die untere Kugel muss also schneller am Ziel sein.
Aber woher weiß ich, dass das was ich abziehe auch wirklich positiv ist? Dies gilt ja nur für  und damit für und damit für  . .
Ist das gegeben?
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 21. Okt 2009 23:25 Titel: TomS Verfasst am: 21. Okt 2009 23:25 Titel: |
 |
|
Also zunächst mal hast du recht, der eine Index fehlt; werde ich korrigieren.
In deinem Fall weißt du natürlich, dass das mittlere Stück (die Kuhle) mit größerer Geschwindigkeit durchlaufen wird, da hier die potentielle Energie geringer, also die kinetische Energie höher ist.
Für eine extrem kurze, flache Kuhle mag nun die höhere Geschwindigkeit einen zu kleinen Zeitgewinn bringen, der durch die größere NBahnlänge wieder aufgezehrt wird. In deinem Fall wird die Länge der Kuhle, über die die Kugel ihre höhere Geschwindigkeit ausspielen kann die etwas längere Wegstrecke (in die Kuhle hinein und wieder hinaus) sicher ausgleichen.
Zu deiner letzten Überlegung: es gilt
 = T_1 - s_2 \frac{v_2 - v_1}{v_1 v_2})
Und natürlich ist die Geschwindigkeitsdifferenz positiv, da ja das oben bezüglich der Energie gesagte gilt: geringere potentielle bedeutet höhere kinetische Energie und damit größere Geschwindigkeit
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Veryyy
Anmeldungsdatum: 14.08.2009
Beiträge: 142
|
 Veryyy Verfasst am: 21. Okt 2009 23:39 Titel: Veryyy Verfasst am: 21. Okt 2009 23:39 Titel: |
 |
|
| Zitat: | | In deinem Fall weißt du natürlich, dass das mittlere Stück (die Kuhle) mit größerer Geschwindigkeit durchlaufen wird, da hier die potentielle Energie geringer, also die kinetische Energie höher ist. |
Dann ist bei deiner Rechnung also 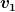 die Geschwindigkeit in der Kuhle. Das hat mich nur etwas verwirrt, weil ich in meiner Zeichnung die Geschwindigkeit in der Kuhle mit die Geschwindigkeit in der Kuhle. Das hat mich nur etwas verwirrt, weil ich in meiner Zeichnung die Geschwindigkeit in der Kuhle mit 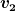 bezeichnet habe. Aber wenn bei dir bezeichnet habe. Aber wenn bei dir  die Geschwindigkeit in der Kuhle ist, stimme ich zu, dass sie größer ist. die Geschwindigkeit in der Kuhle ist, stimme ich zu, dass sie größer ist.
| Zitat: | Für eine extrem kurze, flache Kuhle mag nun die höhere Geschwindigkeit einen zu kleinen Zeitgewinn bringen, der durch die größere NBahnlänge wieder aufgezehrt wird. In deinem Fall wird die Länge der Kuhle, über die die Kugel ihre höhere Geschwindigkeit ausspielen kann die etwas längere Wegstrecke (in die Kuhle hinein und wieder hinaus) sicher ausgleichen.
|
Genau da liegt noch mein kleines Problem. Also ich habe deine Begründung durchaus verstanden. Ich habe ja selbst am Anfang so argumentiert.
Mittlerweile glaube ich aber, dass egal wie klitzeklein die Kuhle ist, Kugel B immer schneller ankommt.(dass also der zusätzliche Weg gar keine Rolle spielt, da er nicht in x-Richtung ist, sondern in y-Richtung) Ich sehe nämlich das Hinabrollen in die Kuhle als Überlagerung von zwei Bewegungen. Zum einen der horizontalen Bewegung (die immer gleich groß ist wie die der Kugel A). Diese wird dann nur vom Weg nach unten überlagert, der die Geschwindigkeit der Bewegung nach rechts nicht beeinflusst. So kann B nur schneller sein als A, weil sie zwischendrin noch eine Überlagerung mit einer zusätzlichen Geschwindigkeit hat.
Was sagst du dazu, ist diese Betrachtungsweise möglich?
|
|
 |
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
 Gajeryis Verfasst am: 22. Okt 2009 00:13 Titel: Gajeryis Verfasst am: 22. Okt 2009 00:13 Titel: |
 |
|
| Veryyy hat Folgendes geschrieben: | | Mittlerweile glaube ich aber, dass egal wie klitzeklein die Kuhle ist, Kugel B immer schneller ankommt.(dass also der zusätzliche Weg gar keine Rolle spielt, da er nicht in x-Richtung ist, sondern in y-Richtung) Ich sehe nämlich das Hinabrollen in die Kuhle als Überlagerung von zwei Bewegungen. Zum einen der horizontalen Bewegung (die immer gleich groß ist wie die der Kugel A). |
Genau dieser Punkt ist nicht ganz richtig. Die Geschwindigkeit, die du per Energieerhaltung errechnest, ist der Geschwindigkeitsbetrag, nicht die Komponente in horizontaler Richtung!
Das heisst, in dem Moment, wo die Kugel B abzweigt, hat sie noch die selbe Geschwindigkeit wie Kugel A, ein Teil der Geschwindigkeit zweigt sich aber in die Vertikalbewegung ab. Treiben wir's ins Extrem: Die Abzweigung sei senkrecht. Während Kugel A fröhlich vorwärtsrollt, fällt B an der selben Stelle abwärts und beschleunigt dabei. Horizontal kommt sie aber nicht voran.
Deshalb muss die horizontale Strecke, in der der volle Geschwindigkeitsbetrag für die Horizontalbewegung ausgenutzt werden kann, genügend lang sein, um die längere Strecke in den Abzweigungen kompensieren zu können.
Dies führt auch zu den komplizierten Integralausdrücken. Nicht jede Bahn ist schneller als die Gerade.
| TomS hat Folgendes geschrieben: | | Dass sich eklige Integrale ergeben, ist klar. Aber Mathematica sollte das schon schaffen ... |
Wenn man Mathematica hat... joa. Aber der Wolfram-Rechner arbeitet ja auch mit einer Mathematica-Umgebung.
Bei einer meiner Lösungsversuche kriegte ich als Zwischenlösung ein Integral in der Form

Die Lösung dieses Integrals gibt eine "überaus übersichtliche" Formel. *lach*
Bin mir aber gerade am überlegen, ob die Brachistochrone nicht mit numerischer Mathematik (Methode der kleinsten Quadrate) gefunden werden könnte.
Für jeden Abschnitt zwischen zwei Stützstellen ergibt sich eine Gleichung für die benötigte Zeit. Daraus ergibt sich ein Gleichungssystem Ax - b = r, wobei r der Residualvektor mit den Abschnittszeiten ist, x die y-Koordinate der Stützstellen. Die Norm von r minimeren ist gleichbedeutend mit Minimierung der Laufzeit. Zum Glück rechnet sich sowas mit MATLAB sehr einfach. Dadurch sollte ich auf die optimale Lage der Stützstellen kommen, welche dann die Brachistochrone nachbilden sollten.
Hm. Versuche ich aber nicht mehr heute. 
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 22. Okt 2009 00:45 Titel: TomS Verfasst am: 22. Okt 2009 00:45 Titel: |
 |
|
| Veryyy hat Folgendes geschrieben: | Dann ist bei deiner Rechnung also 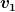 die Geschwindigkeit in der Kuhle. Das hat mich nur etwas verwirrt, weil ich in meiner Zeichnung die Geschwindigkeit in der Kuhle mit die Geschwindigkeit in der Kuhle. Das hat mich nur etwas verwirrt, weil ich in meiner Zeichnung die Geschwindigkeit in der Kuhle mit 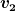 bezeichnet habe. Aber wenn bei dir bezeichnet habe. Aber wenn bei dir  die Geschwindigkeit in der Kuhle ist, stimme ich zu, dass sie größer ist. die Geschwindigkeit in der Kuhle ist, stimme ich zu, dass sie größer ist. |
Nein! 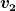 ist die größere der beiden Geschwindigkeiten, also die in der Kuhle, sonst wäre auch die Differenz nicht positiv. ist die größere der beiden Geschwindigkeiten, also die in der Kuhle, sonst wäre auch die Differenz nicht positiv.
Evtl. verwirrt es dich, dass ich nur zwei Streckenabschnitte betrachte. Ich lasse die erste Gefällestrecke und die letzte flache Strecke weg, da hier beide Kugeln offensichtlich die selbe Geschwindigkeit haben und somit keine neuen Beiträge zur Zeitdifferenz entstehen.
| Veryyy hat Folgendes geschrieben: | | ... dass also der zusätzliche Weg gar keine Rolle spielt, ... Diese wird dann nur vom Weg nach unten überlagert, der die Geschwindigkeit der Bewegung nach rechts nicht beeinflusst. |
Siehe dazu die Gajeryis' Antwort.
Anderes Gegenbeispiel zu deinem Argument wäre wieder die Brachistochrone: Man könnte geneigt sein, die Kurve nach unten unendlich auszudehnen, um der Kugel unendlich hohe Geschwindigkeit mitzugeben.Das funktioniert aber offensichtlich nicht. Du musst also schon für eine bestimmte Kuhle beweisen, ob der längere Weg eine Rolle spielt oder nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 22. Okt 2009 01:04 Titel: TomS Verfasst am: 22. Okt 2009 01:04 Titel: |
 |
|
Noch eine kleine Vereinfachung:
Nehmen wir an, die Kugel starte mit Geschwindigkeit Null. Falls nein, können wir das dadurch ereichen, dass wir sie eben davor entlang eines neuen Kurvenstücks von Null auf diese Geschwindigkeit beschleunigen.
Nehmen wir weiter an, der so definierte Startpunkt der Kurve liege bei Höhe Null, d.h. die Energie sei zu Beginn exakt Null.
Dann ergibt sich die klassische Aufgabenstellung:
}{-h(x)} })
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Brillant

Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
 Brillant Verfasst am: 29. Sep 2021 18:49 Titel: Brillant Verfasst am: 29. Sep 2021 18:49 Titel: |
 |
|
| Veryyy hat Folgendes geschrieben: | | Ich habe mir jetzt noch überlegt, dass Kugel B immer schneller ankommen muss |
Ich kenne das Experiment und weiß, dass das so ist.
Aber gedanklich ist das nicht so klar. Beide Kugeln sind bis zum Anfang der Kuhle gleich schnell. Während Kugel B den Abhang runterrollt, bleibt sie in X-Richtung gegenüber Kugel A zurück. Nochmals, wenn sie den Abhang wieder hochrollt.
Demnach müsste die Länge der Kuhle dafür verantwortlich sein, ob Kugel B eher am Ziel ist.
Wie der alte Psychomedes schon sagte:
Einmal Abhang runter und sofort wieder rauf
macht die Kugel zwar munter, aber hält sie auch auf.
_________________
Glaubt nicht dem Hörensagen ... oder eingewurzelten Anschauungen, auch nicht den Worten eines verehrten Meisters; sondern was ihr selbst gründlich geprüft und als euch selbst und anderen zum Wohle dienend erkannt habt, das nehmt an. Siddhartha Gautama |
|
 |
Kurt
Anmeldungsdatum: 20.06.2021
Beiträge: 788
Wohnort: Bayern
|
 Kurt Verfasst am: 29. Sep 2021 22:21 Titel: Re: Welche Kugel kommt schneller unten an? Kurt Verfasst am: 29. Sep 2021 22:21 Titel: Re: Welche Kugel kommt schneller unten an? |
 |
|
| Veryyy hat Folgendes geschrieben: |
3. Beide Effekte heben sich genau auf. Beide Kugeln kommen gleichzeitig am Ende an.
|
Ich meine, dass das nicht stimmt.
Die Kugel mit auf/ab braucht länger bis sie ankommt.
Grund. die Effekte heben sich nicht auf.
Kurt
|
|
 |
istdochklar
Gast
|
 istdochklar Verfasst am: 29. Sep 2021 23:34 Titel: istdochklar Verfasst am: 29. Sep 2021 23:34 Titel: |
 |
|
|
Zu Fuss kommst imemr schneller über den Berg also ist die Lösung hier ja klar.
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3419
|
|
 |
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 985
|
 Frankx Verfasst am: 30. Sep 2021 08:46 Titel: Frankx Verfasst am: 30. Sep 2021 08:46 Titel: |
 |
|
| Brillant hat Folgendes geschrieben: | | Demnach müsste die Länge der Kuhle dafür verantwortlich sein, ob Kugel B eher am Ziel ist. |
Nicht die Länge allein, sondern die geometrische Form insgesamt.
In den gängigen Experimenten ist die Kugel auf der Bahn mit Kuhle schneller.
Man kann sich aber auch leicht eine andere Kuhle vorstellen (oder bauen), bei der die Kugel mehr Zeit benötigt, als auf der direkten geraden Linie.
Die ideale (schnellste) Linie ist die Brachistochrone.
.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 30. Sep 2021 08:59 Titel: TomS Verfasst am: 30. Sep 2021 08:59 Titel: |
 |
|
| Brillant hat Folgendes geschrieben: | | Demnach müsste die Länge der Kuhle dafür verantwortlich sein, ob Kugel B eher am Ziel ist. |
Eigentlich haben wir das oben alles schon erklärt; man muss nur noch die Formeln diskutieren ;-)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Kurt
Anmeldungsdatum: 20.06.2021
Beiträge: 788
Wohnort: Bayern
|
 Kurt Verfasst am: 30. Sep 2021 09:04 Titel: Kurt Verfasst am: 30. Sep 2021 09:04 Titel: |
 |
|
Dieses Ergebnis ist eindeutig.
Aber was ist wenn die Anordnung so ist wie in der Zeichnung?
Kurt
|
|
 |
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 985
|
 Frankx Verfasst am: 30. Sep 2021 09:46 Titel: Frankx Verfasst am: 30. Sep 2021 09:46 Titel: |
 |
|
| Zitat: | | Eigentlich haben wir das oben alles schon erklärt; |
Interessanter ist, welche Anwendungsmöglichkeiten in Technik und Natur in Frage kommen.
Ich könnte mir vorstellen, dass das in bestimmten Sportarten (z.B. Bahnradsport) eine Rolle spielt.
Wäre es eventuell sinnvoll den Effekt bei Straßen oder Schienen zumindest teilweise zu nutzen?
In der Natur kann man bei manchen Vögeln beobachten, dass sie nicht einfach geradeaus fliegen. Sie holen in kleinen Bögen immer wieder Schwung.
Auch kurz vor der Landung auf einem Ast steigen sie wieder etwas auf, selbst wenn sie von weiter oben gestartet sind und der direkte Flug auf einer Geraden möglich wäre.
Allerdings spielen hier sicher noch andere zusätzliche aerodynamische Fragen eine Rolle.
Wer kennt noch andere Möglichkeiten oder hat den Effekt in der Natur beobachtet?
.
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 30. Sep 2021 10:34 Titel: DrStupid Verfasst am: 30. Sep 2021 10:34 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Eigentlich haben wir das oben alles schon erklärt; man muss nur noch die Formeln diskutieren ;-) |
Vor allem müssen wir sie korrigieren. In Deiner Formel für die stückweise flache Strecke fehlen die oben schon mehrfach erwähnten Zeiten für die vertikale Bewegung. Die vollständige Gleichung lautet
})
Im vorliegenden Fall ergibt sich daraus die Zeitdifferenz
 + 2 \cdot \frac{{\left| {v_2 - v_1 } \right|}}{g})
und somit Antwort 1 für

Antwort 2 für

und Antwort 3 für

|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 30. Sep 2021 11:08 Titel: TomS Verfasst am: 30. Sep 2021 11:08 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Eigentlich haben wir das oben alles schon erklärt; man muss nur noch die Formeln diskutieren ;-) |
Vor allem müssen wir sie korrigieren. In Deiner Formel für die stückweise flache Strecke fehlen die oben schon mehrfach erwähnten Zeiten für die vertikale Bewegung. |
Meine Formel gilt natürlich für einen Spezialfall, erklärt aber das wesentliche. Der allgemeine Fall folgt aus dem Integral.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 30. Sep 2021 11:24 Titel: DrStupid Verfasst am: 30. Sep 2021 11:24 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Meine Formel gilt natürlich für einen Spezialfall, erklärt aber das wesentliche. |
Die Formel basiert auf einer falschen Annahme (dass die Geschwindigkeit einen instantanen Sprung macht) und führt deshalb zu einer falschen Schlussfolgerung (dass Kugel B immer schneller ankommt). Was soll damit erklärt werden?
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 30. Sep 2021 13:28 Titel: Myon Verfasst am: 30. Sep 2021 13:28 Titel: |
 |
|
|
Kann leider nur kurz schreiben, da ich im Spital liege. Frage mich aber: ist die Kugel in B nicht immer früher am Ziel, unabhängig von der Kuhlenlänge? Betrachtet man nur die Kräfte, die in horizontaler Richtung wirken sowie die horizontale Geschwindigkeitskomponente, so nimmt letztere zu Beginn der Kuhle infolge der Normalkräfte zu und am Ende der Kuhle wieder ab. Also ist die horizontale Geschwindigkeitskomponente an jedem Ort grösser oder gleich derjenigen in A. Voraussetzung neben fehlender Reibung ist einzig, dass die Kugel nie abhebt. Oder übersehe ich da etwas?
|
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3419
|
 ML Verfasst am: 30. Sep 2021 13:47 Titel: ML Verfasst am: 30. Sep 2021 13:47 Titel: |
 |
|
Hallo,
| Myon hat Folgendes geschrieben: | Frage mich aber: ist die Kugel in B nicht immer früher am Ziel, unabhängig von der Kuhlenlänge?
|
Wenn Du die Kuhle unendlich tief machst, kommt die Kugel auf der gekrümmten Bahn auf jeden Fall später an, egal, wie lang die Bahn "unten" ist.
Viele Grüße
Michael
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 30. Sep 2021 13:51 Titel: Myon Verfasst am: 30. Sep 2021 13:51 Titel: |
 |
|
|
PS: Sehe, dass Veryyy oben schon genau dasselbe geschrieben hatte. Das gilt für diesen Fall einer horizontalen, geraden Strecke. Bei einer schiefen, geraden Strecke gilt es sehr wahrscheinlich schon nicht mehr allgemein. Die horizontale Komponente der Hangabtriebskraft erreicht wahrscheinlich bei einer Neigung von 45 Grad ein Maximum. Kann leider momentan nur so etwas gedanklich herumsinnieren und nichts rechnen.
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 30. Sep 2021 14:31 Titel: DrStupid Verfasst am: 30. Sep 2021 14:31 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | Voraussetzung neben fehlender Reibung ist einzig, dass die Kugel nie abhebt. |
Das müsste selbst dann gelten, wenn die Kugel abhebt. Du meinst vermutlich, dass keine Kräfte außer Schwerkraft und Normalkraft wirken dürfen.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 30. Sep 2021 14:47 Titel: Myon Verfasst am: 30. Sep 2021 14:47 Titel: |
 |
|
Das mit der Hangabtriebskraft war Blödsinn. Die Normalkraft hängt von der Geschwindigkeit ab.
Wenn die Kugel abhebt, wird sie in horizontaler Richtung nicht beschleunigt. Dann ist sie im Beispiel des 1. Beitrags i.a. nicht mehr schneller.
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 30. Sep 2021 14:57 Titel: DrStupid Verfasst am: 30. Sep 2021 14:57 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | Wenn die Kugel abhebt, wird sie in horizontaler Richtung nicht beschleunigt. Dann ist sie im Beispiel des 1. Beitrags i.a. nicht mehr schneller. |
Um in horizontaler Richtung nicht zu beschleunigen, darf Kugel B in der Kuhle nur im freien Fall unterwegs sein und zwischendurch elastisch abprallen. Sobald an irgend einer Stelle eine Hangabtriebskraft auftritt, wird sie Kugel A überholen. Langsamer als Kugel A kann sie in horizontaler Richtung nur werden, wenn es Zwangskräfte gibt, die ein Abheben verhindern.
PS: Dabei gehe ich davon aus, dass die Kugel gleitet. Wenn sie ohne Schlupf rollt, dann wird es komplizierter.
|
|
 |
Brillant

Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
 Brillant Verfasst am: 01. Okt 2021 00:14 Titel: Brillant Verfasst am: 01. Okt 2021 00:14 Titel: |
 |
|
Hallo Michael. Ich sehe meine Theorie bekräftigt. Im ersten Beispiel hat die Kugel (grün) durch die lange Gerade einen deutlichen Vorsprung.
Im zweiten Beispiel sind die drei Talstrecken zusammen deutlich kürzer als die lange Kuhle aus 1 und der Vorsprung des Talfahrers ist gerade mal zwei Kugeldurchmesser.
Was ich noch nicht ganz verstehe: Wieso bleiben die Talfahrer auf ihrer (ihren) Abwärts-Strecken nicht x-mäßig zurück?
Gruß, Brilli
| Beschreibung: |
|
| Dateigröße: |
74.02 KB |
| Angeschaut: |
3863 mal |

|
| Beschreibung: |
|
| Dateigröße: |
134.11 KB |
| Angeschaut: |
3863 mal |

|
_________________
Glaubt nicht dem Hörensagen ... oder eingewurzelten Anschauungen, auch nicht den Worten eines verehrten Meisters; sondern was ihr selbst gründlich geprüft und als euch selbst und anderen zum Wohle dienend erkannt habt, das nehmt an. Siddhartha Gautama |
|
 |
|

















 Ich habe seit Eröffnung des Threads mehrere A4 Seiten vollgekritzelt, im Versuch, die Brachistochrone herzuleiten bzw. die Laufzeit anderer Kurven zu rechnen. Die Herleitung der Brachistochrone auf Wikipedia kapiere ich mittlerweile, aber wie sie auf den parametrisierten Ansatz gekommen sind, entfällt jeglicher Erkenntnis meinerseits. Aber ich bin auch kein Mathematiker.
Ich habe seit Eröffnung des Threads mehrere A4 Seiten vollgekritzelt, im Versuch, die Brachistochrone herzuleiten bzw. die Laufzeit anderer Kurven zu rechnen. Die Herleitung der Brachistochrone auf Wikipedia kapiere ich mittlerweile, aber wie sie auf den parametrisierten Ansatz gekommen sind, entfällt jeglicher Erkenntnis meinerseits. Aber ich bin auch kein Mathematiker.


