| Autor |
Nachricht |
Physik_Student
Anmeldungsdatum: 01.07.2021
Beiträge: 26
|
 Physik_Student Verfasst am: 26. Aug 2021 20:54 Titel: Potential aus Kraft berechnen? Physik_Student Verfasst am: 26. Aug 2021 20:54 Titel: Potential aus Kraft berechnen? |
 |
|
Meine Frage:
Hallo,
ich muss in einer Aufgabe das Potential V zu folgender Kraft berechnen:
\vec{e}_x+(x-2y)\vec{e}_y)
Ich habe allerdings 2 Probleme:
1.) Welche Integrationsgrenzen soll ich nehmen? oder soll ich das Integral unbestimmt lassen? (In der Aufgabe ist nur die Kraft gegeben, mehr nicht)
2.) In meinem Integral stehen noch die Einheitsvektoren drin, inwiefern muss ich diese berücksichtigen?
Danke Im Voraus!
Meine Ideen:
Da gilt:
=-\nabla V)
hätte ich wie folgt gerechnet:
d\vec{r}=-\int (y-4x)\vec{e}_xd\vec{x}-\int (x-2y)\vec{e}_yd\vec{y}=?) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 26. Aug 2021 21:28 Titel: Re: Potential aus Kraft berechnen? index_razor Verfasst am: 26. Aug 2021 21:28 Titel: Re: Potential aus Kraft berechnen? |
 |
|
| Physik_Student hat Folgendes geschrieben: | Meine Frage:
Hallo,
ich muss in einer Aufgabe das Potential V zu folgender Kraft berechnen:
\vec{e}_x+(x-2y)\vec{e}_y)
Ich habe allerdings 2 Probleme:
1.) Welche Integrationsgrenzen soll ich nehmen? oder soll ich das Integral unbestimmt lassen? (In der Aufgabe ist nur die Kraft gegeben, mehr nicht)
|
Du wählst irgendeinen beliebigen Punkt ) , an dem du irgendeinen Wert , an dem du irgendeinen Wert ) des Potentials vorgibst. An jedem Punkt P=(x,y) hat dann das Potential den Wert des Potentials vorgibst. An jedem Punkt P=(x,y) hat dann das Potential den Wert
 = V(P_0) - \int_0^1 \vec{F}(\gamma(t))\dot \gamma(t)\dd t,)
wobei  irgendeine Kurve ist, mit irgendeine Kurve ist, mit =P_0) und und =P) , z.B. , z.B.
 = P_0 + t(P - P_0).)
Am sinnvollsten ist es  und und 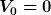 zu wählen. zu wählen.
Der Wert des Integrals hängt nicht von der Wahl der Kurve ab. Andernfalls hätte 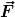 überhaupt kein Potential. Aber wenn es eins hat, dann hat es natürlich gleich unendlich viele. Die Aufgabe müßte also eigentlich lauten "Bestimme ein Potential..." oder Zusatzbedingungen angeben, die die Lösung eindeutig machen. überhaupt kein Potential. Aber wenn es eins hat, dann hat es natürlich gleich unendlich viele. Die Aufgabe müßte also eigentlich lauten "Bestimme ein Potential..." oder Zusatzbedingungen angeben, die die Lösung eindeutig machen.
| Zitat: |
2.) In meinem Integral stehen noch die Einheitsvektoren drin, inwiefern muss ich diese berücksichtigen?
|
Unter dem Integral steht das Skalarprodukt von )) mit dem Tangentialvektor mit dem Tangentialvektor ) . Für die oben von mir gewählte Kurve ist z.B. . Für die oben von mir gewählte Kurve ist z.B.  = (x-x_0)\vec{e}_x + (y-y_0)\vec{e}_y) . Damit müßtest du eigentlich erstmal weiterkommen. . Damit müßtest du eigentlich erstmal weiterkommen. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 26. Aug 2021 21:38 Titel: Re: Potential aus Kraft berechnen? DrStupid Verfasst am: 26. Aug 2021 21:38 Titel: Re: Potential aus Kraft berechnen? |
 |
|
| Physik_Student hat Folgendes geschrieben: | | 2.) In meinem Integral stehen noch die Einheitsvektoren drin, inwiefern muss ich diese berücksichtigen? |
Das ist nur eine Möglichkeit, den Vektor F zu schreiben. Du suchst ein V mit

 |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 26. Aug 2021 21:38 Titel: schnudl Verfasst am: 26. Aug 2021 21:38 Titel: |
 |
|
Sicherheitshalber würde ich bei solchen Aufgaben erst prüfen, ob es überhaupt ein Potenzial gibt. Falls ja, kannst du den dir am einfachsten erscheinenden Weg für die Integration wählen.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 26. Aug 2021 21:54 Titel: index_razor Verfasst am: 26. Aug 2021 21:54 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: | | Sicherheitshalber würde ich bei solchen Aufgaben erst prüfen, ob es überhaupt ein Potenzial gibt. |
Da F auf der ganzen Ebene definiert ist, reicht dafür die Bedingung  zu prüfen. zu prüfen. |
|
 |
Physik_Student
Anmeldungsdatum: 01.07.2021
Beiträge: 26
|
 Physik_Student Verfasst am: 26. Aug 2021 23:35 Titel: Re: Potential aus Kraft berechnen? Physik_Student Verfasst am: 26. Aug 2021 23:35 Titel: Re: Potential aus Kraft berechnen? |
 |
|
| Zitat: |
wobei  irgendeine Kurve ist, mit irgendeine Kurve ist, mit =P_0) und und =P) , z.B. , z.B.
 = P_0 + t(P - P_0).) |
Da die Kraft konservativ sein muss, wenn ein Potential existiert, kann ich den Weg frei Wählen, richtig? D.h. für Zentralkräfte könnte ich z.B. immer die von dir vorgeschlagene Gleichung nehmen, die ja einen geraden Weg beschreibt, oder? (also für t=0 ist man bei P_0 und für t=1 bei P). Stimmt das so?
| Zitat: | Unter dem Integral steht das Skalarprodukt von )) mit dem Tangentialvektor mit dem Tangentialvektor ) . Für die oben von mir gewählte Kurve ist z.B. . Für die oben von mir gewählte Kurve ist z.B.  = (x-x_0)\vec{e}_x + (y-y_0)\vec{e}_y) |
Ich schreibe mal auf, wie ich das verstehe:
=V_0-\int\limits_0^1F(\vec{\gamma})\dot{\gamma}dt=V_0-\int\limits_0^1F(\vec{\gamma})\cdot ((x-x_0)\vec{e}_x+(y-y_0)\vec{e}_y)dt=)
\vec{e}_x+(x-2y)\vec{e}_y)\cdot ((x-x_0)\vec{e}_x+(y-y_0)\vec{e}_y)dt=-\int\limits_0^1((y-4x)x+(x-2y)y)dt=2(2x^2+y^2-xy))
Dabei habe ich im vorletzten Schritt die Bedingungen x_0=y_0=0 und V_0=0 eingesetzt und verwendet, dass gilt:
^2=(\vec{e}_x)^2=1 \wedge \vec{e}_y\cdot\vec{e}_x=0) |
|
 |
Physik_Student
Anmeldungsdatum: 01.07.2021
Beiträge: 26
|
 Physik_Student Verfasst am: 26. Aug 2021 23:40 Titel: Physik_Student Verfasst am: 26. Aug 2021 23:40 Titel: |
 |
|
| Zitat: | | Sicherheitshalber würde ich bei solchen Aufgaben erst prüfen, ob es überhaupt ein Potenzial gibt. |
Stimmt, das ist sinnvoll, war hier allerdings schon in der a) verlangt. Bzw. man sollte prüfen, ob die Kraft konservativ ist und wenn sie es ist, dann existiert ja auch ein Potential, oder? |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 27. Aug 2021 06:26 Titel: Re: Potential aus Kraft berechnen? Myon Verfasst am: 27. Aug 2021 06:26 Titel: Re: Potential aus Kraft berechnen? |
 |
|
| Physik_Student hat Folgendes geschrieben: | =(\dots)=2(2x^2+y^2-xy)) |
Nur kurz, ich will nicht dreinfunken, aber so hast Du schneller ein Feedback: wenn Du das überprüfst, indem Du den Gradienten darauf anwendest, siehst Du, dass ein Faktor 2 zuviel ist. Bei der Funktion  ging ein Faktor t vergessen, denn es soll ja gelten ging ein Faktor t vergessen, denn es soll ja gelten
| index_razor hat Folgendes geschrieben: |  = P_0 + t(P - P_0).) |
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Aug 2021 08:42 Titel: Re: Potential aus Kraft berechnen? index_razor Verfasst am: 27. Aug 2021 08:42 Titel: Re: Potential aus Kraft berechnen? |
 |
|
| Physik_Student hat Folgendes geschrieben: | | Zitat: |
wobei  irgendeine Kurve ist, mit irgendeine Kurve ist, mit =P_0) und und =P) , z.B. , z.B.
 = P_0 + t(P - P_0).) |
Da die Kraft konservativ sein muss, wenn ein Potential existiert, kann ich den Weg frei Wählen, richtig?
|
Ja, wenn ein Potential existiert, dann findest du eins als Wegintegral über F entlang einer beliebigen Kurve von einem fixen Ausgangspunkt. Ob ein Potential existiert, ist nicht immer ganz trivial zu entscheiden. Aber in diesem Fall ist es das.
| Zitat: |
D.h. für Zentralkräfte könnte ich z.B. immer die von dir vorgeschlagene Gleichung nehmen, die ja einen geraden Weg beschreibt, oder? (also für t=0 ist man bei P_0 und für t=1 bei P). Stimmt das so?
|
Man kann ihn nicht immer wählen, da es sein kann, daß der Definitionsbereich von F nicht sternförmig ist. Ein Gebiet ist sternförmig, wenn es einen Punk 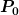 enthält, von dem aus man alle anderen seiner Punkte durch Geraden erreichen kann. Genau diese Eigenschaft habe ich ja benutzt. enthält, von dem aus man alle anderen seiner Punkte durch Geraden erreichen kann. Genau diese Eigenschaft habe ich ja benutzt.
Das Problem besteht z.B. auch bei  . Da kannst du weder vom Nullpunkt aus, noch über den Nullpunkt hinweg integrieren. Andererseits spielt das Problem natürlich gerade bei Zentralfeldern keine praktische Rolle. Da die Kraft nur von r abhängt, gibt es auch ein Potential, daß nur von r abhängt. Du kannst also von irgendeinem Radius . Da kannst du weder vom Nullpunkt aus, noch über den Nullpunkt hinweg integrieren. Andererseits spielt das Problem natürlich gerade bei Zentralfeldern keine praktische Rolle. Da die Kraft nur von r abhängt, gibt es auch ein Potential, daß nur von r abhängt. Du kannst also von irgendeinem Radius  ausgehen und lediglich in radialer Richtung integrieren. Das Ergebnis V(r) ist dann natürlich dasselbe für alle Punkte mit demselben r. ausgehen und lediglich in radialer Richtung integrieren. Das Ergebnis V(r) ist dann natürlich dasselbe für alle Punkte mit demselben r.
| Zitat: |
| Zitat: | Unter dem Integral steht das Skalarprodukt von )) mit dem Tangentialvektor mit dem Tangentialvektor ) . Für die oben von mir gewählte Kurve ist z.B. . Für die oben von mir gewählte Kurve ist z.B.  = (x-x_0)\vec{e}_x + (y-y_0)\vec{e}_y) |
Ich schreibe mal auf, wie ich das verstehe:
=V_0-\int\limits_0^1F(\vec{\gamma})\dot{\gamma}dt=V_0-\int\limits_0^1F(\vec{\gamma})\cdot ((x-x_0)\vec{e}_x+(y-y_0)\vec{e}_y)dt=)
\vec{e}_x+(x-2y)\vec{e}_y)\cdot ((x-x_0)\vec{e}_x+(y-y_0)\vec{e}_y)dt=-\int\limits_0^1((y-4x)x+(x-2y)y)dt=2(2x^2+y^2-xy))
|
Hier hast du anscheinend vergessen die Kurve in F einzusetzen. Für die x-Komponente von )) müßte sonst bei dir müßte sonst bei dir  + y_0+ 4(t(x-x_0) + x_0)]\vec{e}_x) stehen und etwas ähnliches für die y-Komponente. stehen und etwas ähnliches für die y-Komponente.
Ich führe mal ein paar Zwischenschritte vor, setze aber von Anfang an  damit die Formeln nicht so lang werden. Du kannst das ja dann nochmal für andere Punkte durchführen und dir so den Einfluß der Wahl des Startpunkts auf das Ergebnis klarmachen. damit die Formeln nicht so lang werden. Du kannst das ja dann nochmal für andere Punkte durchführen und dir so den Einfluß der Wahl des Startpunkts auf das Ergebnis klarmachen.
Also, wir haben ein Vektorfeld  = \vec{F}(x,y)) . Die Kurve hat, sagen wir, die Komponenten . Die Kurve hat, sagen wir, die Komponenten  = (\xi(t), \eta(t)) = (tx, ty))
Setzen wir den Punkt  = (\xi(t), \eta(t)) auf der Kurve in das Vektorfeld ein, dann erhalten wir also auf der Kurve in das Vektorfeld ein, dann erhalten wir also
) = \vec{F}(\xi(t), \eta(t)) = (\eta(t) - 4\xi(t))\vec{e}_x + (\xi(t) - 2\eta(t))\vec{e}_y\\= t\left[ (y-4x)\vec{e}_x + (x-2y)\vec{e}_y\right] )
Zusammen mit  = x\vec{e}_x + y\vec{e}_y) kommt dann also zu dem Integranden, den du ausgerechnet hat noch ein zusätzlicher Faktor t und damit der fehlende Faktor 1/2 in das Ergebnis. kommt dann also zu dem Integranden, den du ausgerechnet hat noch ein zusätzlicher Faktor t und damit der fehlende Faktor 1/2 in das Ergebnis. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 27. Aug 2021 09:21 Titel: DrStupid Verfasst am: 27. Aug 2021 09:21 Titel: |
 |
|
Ich weiß nicht, ob man hier wirklich so einen Aufwand betreiben muss. Da nur die Kraft ohne irgendwelche Einschränkungen gegeben ist, müsste man ihre Komponenten doch direkt integrieren können:
dx = } 2x^2 - xy + A\left( y \right) = \int {\left( {2y - x} \right)dy = } y^2 - xy + B\left( x \right))
Daraus folgen die Integrationskonstanten
 = y^2 + C)
 = 2x^2 + C)
und somit das Potential

Zuletzt bearbeitet von DrStupid am 27. Aug 2021 13:37, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Aug 2021 09:49 Titel: index_razor Verfasst am: 27. Aug 2021 09:49 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | Ich weiß nicht, ob man hier wirklich so einen Aufwand betreiben muss.
|
Das ist überhaupt kein Aufwand, sobald man ganz allgemein verstanden hat, wie Wegintegrale funktionieren. Ich vermute, daß genau das auch Sinn der Aufgabe ist. Und die Erfahrung mit vielen ähnlichen Aufgaben zeigt ja auch, daß das Berechnen solcher Integrale anfangs durchaus ein gewisses Problem darstellt. Also lohnt es sich schon auf ein paar Details einzugehen.
| Zitat: |
Da nur die Kraft ohne irgendwelche Einschränkungen gegeben ist, müsste man ihre Komponenten doch direkt integrieren können:
dx = } 2x^2 - xy + A\left( y \right) = \int {\left( {2y - x} \right)dy = } y^2 - xy + B\left( x \right))
|
Auch diese Rechnung versteht man m.E. besser als Integral entlang eines speziellen Weges, der sich aus zwei achsenparallelen Stücken zusammensetzt, wodurch zuerst  und dann und dann  gilt. Wenn man im Nullpunkt anfängt, dann ist die ganze Rechnung sogar noch kompakter gilt. Wenn man im Nullpunkt anfängt, dann ist die ganze Rechnung sogar noch kompakter
 = \int 4x \dd x + \int (2y - x)\dd y = 2x^2 - xy + y^2 )
Im ersten Integral wird von 0 bis x integriert und y=0 gesetzt. Im zweiten Integral wird von 0 bis y entlang des konstanten Endwerts von x integriert. Ich habe das absichtlich nicht so gerechnet, weil ich erklären wollte, wie man Wegintegrale allgemein berechnet. |
|
 |
Physik_Student
Anmeldungsdatum: 01.07.2021
Beiträge: 26
|
 Physik_Student Verfasst am: 27. Aug 2021 12:49 Titel: Re: Potential aus Kraft berechnen? Physik_Student Verfasst am: 27. Aug 2021 12:49 Titel: Re: Potential aus Kraft berechnen? |
 |
|
| Zitat: |
Das Problem besteht z.B. auch bei  . Da kannst du weder vom Nullpunkt aus, noch über den Nullpunkt hinweg integrieren. Andererseits spielt das Problem natürlich gerade bei Zentralfeldern keine praktische Rolle. Da die Kraft nur von r abhängt, gibt es auch ein Potential, daß nur von r abhängt. Du kannst also von irgendeinem Radius . Da kannst du weder vom Nullpunkt aus, noch über den Nullpunkt hinweg integrieren. Andererseits spielt das Problem natürlich gerade bei Zentralfeldern keine praktische Rolle. Da die Kraft nur von r abhängt, gibt es auch ein Potential, daß nur von r abhängt. Du kannst also von irgendeinem Radius  ausgehen und lediglich in radialer Richtung integrieren. Das Ergebnis V(r) ist dann natürlich dasselbe für alle Punkte mit demselben r. ausgehen und lediglich in radialer Richtung integrieren. Das Ergebnis V(r) ist dann natürlich dasselbe für alle Punkte mit demselben r. |
Danke für das Beispiel, das macht es klarer.
| Zitat: |
Also, wir haben ein Vektorfeld  = \vec{F}(x,y)) . Die Kurve hat, sagen wir, die Komponenten . Die Kurve hat, sagen wir, die Komponenten  = (\xi(t), \eta(t)) = (tx, ty)) |
D.h.  = (\xi(t), \eta(t)) = (tx, ty)) ist einfach eine andere Schreibweise für: ist einfach eine andere Schreibweise für: =P_0+t(P-P_0)) , wie wir es oben definiert hatten, oder? , wie wir es oben definiert hatten, oder?
| Zitat: |
Setzen wir den Punkt  = (\xi(t), \eta(t)) auf der Kurve in das Vektorfeld ein, dann erhalten wir also auf der Kurve in das Vektorfeld ein, dann erhalten wir also
) = \vec{F}(\xi(t), \eta(t)) = (\eta(t) - 4\xi(t))\vec{e}_x + (\xi(t) - 2\eta(t))\vec{e}_y\\= t\left[ (y-4x)\vec{e}_x + (x-2y)\vec{e}_y\right] )
|
damit komme ich jetzt auch auf das richtige Ergebnis! |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Aug 2021 13:01 Titel: Re: Potential aus Kraft berechnen? index_razor Verfasst am: 27. Aug 2021 13:01 Titel: Re: Potential aus Kraft berechnen? |
 |
|
| Physik_Student hat Folgendes geschrieben: |
| Zitat: |
Also, wir haben ein Vektorfeld  = \vec{F}(x,y)) . Die Kurve hat, sagen wir, die Komponenten . Die Kurve hat, sagen wir, die Komponenten  = (\xi(t), \eta(t)) = (tx, ty)) |
D.h.  = (\xi(t), \eta(t)) = (tx, ty)) ist einfach eine andere Schreibweise für: ist einfach eine andere Schreibweise für: =P_0+t(P-P_0)) , wie wir es oben definiert hatten, oder? , wie wir es oben definiert hatten, oder?
|
Ja, genau. Als 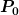 habe ich den Ursprung gewählt, also habe ich den Ursprung gewählt, also ) , P ist einfach irgendein Punkt mit den Koordinaten x,y und , P ist einfach irgendein Punkt mit den Koordinaten x,y und , \eta(t)) sind jeweils x- und y-Koordinate des Punktes sind jeweils x- und y-Koordinate des Punktes ) auf der Kurve. auf der Kurve.
Also
, \eta(t)) = \gamma(t) = P_0 + t(P - P_0) = (0, 0) + t[(x,y) - (0,0)] = (tx, ty).)
Natürlich kannst du ) auch irgendwo anders hin verlegen. Dann wäre auch irgendwo anders hin verlegen. Dann wäre
 = (x_0 + t(x- x_0), y_0 + t(y-y_0)),)
oder du wählst eine ganz andere Kurve, z.B. die aus meinem letzten Beitrag, die zusammengesetzt ist aus den beiden Teilkurven
 = (tx, 0),\qquad \gamma_2(t) = (x, ty))
(t jeweils von 0 bis 1). Da das Integral wegunabhängig ist, kannst du natürlich die Integrationsstrecke wählen, die du am einfachsten findest. |
|
 |
Physik_Student
Anmeldungsdatum: 01.07.2021
Beiträge: 26
|
 Physik_Student Verfasst am: 27. Aug 2021 13:35 Titel: Re: Potential aus Kraft berechnen? Physik_Student Verfasst am: 27. Aug 2021 13:35 Titel: Re: Potential aus Kraft berechnen? |
 |
|
|
Dann habe ich es jetzt verstanden, vielen Dank für die Mühe! |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 27. Aug 2021 13:54 Titel: DrStupid Verfasst am: 27. Aug 2021 13:54 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Auch diese Rechnung versteht man m.E. besser als Integral entlang eines speziellen Weges, der sich aus zwei achsenparallelen Stücken zusammensetzt, wodurch zuerst  und dann und dann  gilt. gilt. |
Das sehe ich nicht so. Die Integrale sind unbestimmt. Selbst wenn Du sie als Wegintegrale entlang der Achsen interpretierst, kannst Du nicht sagen, dass die zweite Integration dort beginnt, wo die erste endet. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Aug 2021 14:00 Titel: index_razor Verfasst am: 27. Aug 2021 14:00 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | Auch diese Rechnung versteht man m.E. besser als Integral entlang eines speziellen Weges, der sich aus zwei achsenparallelen Stücken zusammensetzt, wodurch zuerst  und dann und dann  gilt. gilt. |
Das sehe ich nicht so. Die Integrale sind unbestimmt.
|
Ja, in deiner Rechnung. Aber das verkompliziert die Sache eben unnötigerweise ein bißchen.
| Zitat: |
Selbst wenn Du sie als Wegintegrale entlang der Achsen interpretierst, kannst Du nicht sagen, dass die zweite Integration dort beginnt, wo die erste endet. |
Doch, das kann ich sagen. Und es vereinfacht die Sache. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 27. Aug 2021 14:10 Titel: DrStupid Verfasst am: 27. Aug 2021 14:10 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Ja, in deiner Rechnung. |
Und ich gehe davon aus, dass Du über meine Rechnung sprichst, wenn Du sie zitierst und etwas darunter schreibst.
| index_razor hat Folgendes geschrieben: | | Aber das verkompliziert die Sache eben unnötigerweise ein bißchen. |
Das ist Ansichtssache. Ich finde es unnötig kompliziert, einen Pfad vorzugeben, der in der Aufgabe nicht erwähnt wird und von dem das Ergebnis grundsätzlich unabhängig sein muss.
| index_razor hat Folgendes geschrieben: | | Doch, das kann ich sagen. |
Dann sprichst Du aber nicht mehr über meine Rechnung. Es wäre weniger missverständlich gewesen, wenn Du geschrieben hättest, dass Du Deinen Rechenweg bevorzugst. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Aug 2021 14:15 Titel: index_razor Verfasst am: 27. Aug 2021 14:15 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Ja, in deiner Rechnung. |
Und ich gehe davon aus, dass Du über meine Rechnung sprichst, wenn Du sie zitierst und etwas darunter schreibst.
|
Tue ich auch. Ich sprach davon, wie man deine Rechnung sogar noch vereinfachen kann, wenn man sie als spezielles Wegintegral auffaßt. Der ganze Punkt war, die Mächtigkeit der Wegintegrale zu zeigen und warum sie ein wichtiges Werkzeug darstellen. Aus genau diesem Grund habe ich aber nicht lediglich diesen Spezialfall diskutiert, sondern das allgemeine Konzept erläutert.
| DrStupid hat Folgendes geschrieben: |
| index_razor hat Folgendes geschrieben: | | Aber das verkompliziert die Sache eben unnötigerweise ein bißchen. |
Das ist Ansichtssache. Ich finde es unnötig kompliziert, einen Pfad vorzugeben, der in der Aufgabe nicht erwähnt wird und von dem das Ergebnis grundsätzlich unabhängig sein muss.
|
Deine Rechnung benutzt auch zwei Pfade in der x-y-Ebene. Das scheint dir gar nicht klar zu sein. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 27. Aug 2021 14:23 Titel: DrStupid Verfasst am: 27. Aug 2021 14:23 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Ich sprach davon, wie man deine Rechnung sogar noch vereinfachen kann, wenn man sie als spezielles Wegintegral auffaßt. |
Du hast davon gesprochen, dass man meine Rechung als Wegintegral verstehen kann. Dem widerspreche ich. Was Du dann als Vereinfachung meiner Rechnung anbietest, ist tatsächlich ein völlig anderer Ansatz.
| index_razor hat Folgendes geschrieben: | | Der ganze Punkt war, die Mächtigkeit der Wegintegrale zu zeigen und warum sie ein wichtiges Werkzeug darstellen. |
Und mein Punkt ist, dass man so ein mächtiges Werkzeug in diesem einfachen Fall gar nicht braucht.
| index_razor hat Folgendes geschrieben: | | Deine Rechnung benutzt auch zwei Pfade in der x-y-Ebene. |
Immerhin hast Du schon verstanden, dass es nicht ein Pfad ist. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Aug 2021 14:28 Titel: index_razor Verfasst am: 27. Aug 2021 14:28 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Ich sprach davon, wie man deine Rechnung sogar noch vereinfachen kann, wenn man sie als spezielles Wegintegral auffaßt. |
Du hast davon gesprochen, dass man meine Rechung als Wegintegral verstehen kann. Dem widerspreche ich. Was Du dann als Vereinfachung meiner Rechnung anbietest, ist tatsächlich ein völlig anderer Ansatz.
|
Wenn du das glaubst, dann hast du es nicht richtig verstanden. (Abgesehen davon, daß dies deiner eigenen Auffassung widerspricht, der Ansatz mittels Wegintegralen sei komplizierter.)
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Der ganze Punkt war, die Mächtigkeit der Wegintegrale zu zeigen und warum sie ein wichtiges Werkzeug darstellen. |
Und mein Punkt ist, dass man so ein mächtiges Werkzeug in diesem einfachen Fall gar nicht braucht.
|
Die Beherrschung der benötigten Werkzeuge lernt man am besten zuerst an einfachen Aufgaben. Gerade dort wo man sie zunächst nicht braucht, kann man dann selbst feststellen, ob die Anwendung erfolgreich war.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Deine Rechnung benutzt auch zwei Pfade in der x-y-Ebene. |
Immerhin hast Du schon verstanden, dass es nicht ein Pfad ist. |
Natürlich habe ich das. Bis auf die Richtungen waren die Pfade aber unbestimmt. Genau deshalb kann ich sie ja zu einem Pfad zusammensetzen und somit das ganze Argument vereinfachen. |
|
 |
gast_free
Anmeldungsdatum: 15.07.2021
Beiträge: 195
|
 gast_free Verfasst am: 27. Aug 2021 14:37 Titel: Re: Potential aus Kraft berechnen? gast_free Verfasst am: 27. Aug 2021 14:37 Titel: Re: Potential aus Kraft berechnen? |
 |
|
ich muss in einer Aufgabe das Potential V zu folgender Kraft berechnen:
Dann wollen wir mal!
\vec{e}_x+(x-2y)\vec{e}_y)
=-\frac{\partial \phi(x,y)}{\partial x}\cdot \vec{e_x}-\frac{\partial \phi(x,y)}{\partial y}\cdot \vec{e_y} )
Also
}{\partial x})
}{\partial y})
Somit
=-\int (y-4x) dx + C_x(y)=-xy+2x^2+C_x(y))
Alternativ
=-\int (x-2y) dy + C_y(x)=-xy+y^2+C_y(x))
Beide Funktionen müssen identisch sein woraus sich die Konstante ergibt.
=y^2)
=2x^2)
Die Potentialfunktion entgültig:
=-xy+2x^2+y^2)
Check:
=-(-y+4x)\cdot \vec{e_x}-(-x+2y)\cdot \vec{e_y}=(y-4x)\cdot \vec{e_x}+(x-2y)\cdot \vec{e_y}) Alles Roger! Alles Roger!
Bemerkung:
=0=>\frac{\partial \phi(x,y)}{\partial x \partial y}=\frac{\partial \phi(x,y)}{\partial y \partial x})
+++ Danke für den Hinweis mit dem Vorzeichen! +++
Zuletzt bearbeitet von gast_free am 27. Aug 2021 15:45, insgesamt einmal bearbeitet |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 27. Aug 2021 14:43 Titel: DrStupid Verfasst am: 27. Aug 2021 14:43 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Die Beherrschung der benötigten Werkzeuge lernt man am besten zuerst an einfachen Aufgaben. |
Wenn hier jemand fragt, wie man eine konkrete Aufgabe löst, dann gehe ich davon aus, dass er wissen will, wie man diese konkrete Aufgabe löst und nicht, wie man Werkzeuge verwendet, die man dafür gar nicht braucht. Ist das so abwegig?
| index_razor hat Folgendes geschrieben: | | Genau deshalb kann ich sie ja zu einem Pfad zusammensetzen und somit das ganze Argument vereinfachen. |
Wenn Du glaubst, dass das dann noch meinem Ansatz entspricht, dann hast Du ihn nicht verstanden. Ist Dir aufgefallen, dass ich die Integrale über die beiden Wege nicht addiere, sondern gleich setze?
PS: Siehe Rechnung von @gast_free. Der macht es genauso wie ich. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 27. Aug 2021 14:48 Titel: Re: Potential aus Kraft berechnen? DrStupid Verfasst am: 27. Aug 2021 14:48 Titel: Re: Potential aus Kraft berechnen? |
 |
|
| gast_free hat Folgendes geschrieben: | }{\partial x}\cdot \vec{e_x}+\frac{\partial \phi(x,y)}{\partial y}\cdot \vec{e_y} ) |

Der Rest stimmt. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Aug 2021 15:04 Titel: index_razor Verfasst am: 27. Aug 2021 15:04 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Die Beherrschung der benötigten Werkzeuge lernt man am besten zuerst an einfachen Aufgaben. |
Wenn hier jemand fragt, wie man eine konkrete Aufgabe löst, dann gehe ich davon aus, dass er wissen will, wie man diese konkrete Aufgabe löst und nicht, wie man Werkzeuge verwendet, die man dafür gar nicht braucht. Ist das so abwegig?
|
Er hat ja schon einen Ansatz präsentiert, der aussah wie ein Wegintegral. Ich halte es deshalb -- sowie auf Grund meiner Erfahrung mit ähnlich klingenden Aufgaben -- nicht für abwegig, daß hier das Konzept der Wegintegrale gelernt werden soll. Und die liefern, nebenbei gesagt, auch für diese Aufgabe die einfachste Lösung. Deswegen braucht man sie auch hier.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Genau deshalb kann ich sie ja zu einem Pfad zusammensetzen und somit das ganze Argument vereinfachen. |
Wenn Du glaubst, dass das dann noch meinem Ansatz entspricht, dann hast Du ihn nicht verstanden. Ist Dir aufgefallen, dass ich die Integrale über die beiden Wege nicht addiere, sondern gleich setze?
|
Ja, ist mir aufgefallen. Das ist ja gerade die vollkommen unnötige Komplikation. Das Gleichsetzen bedeutet nichts anderes, als daß du die Endpunkte der beiden (vorher beliebigen) achsenparallelen Pfade gleichsetzt. Es ist viel einfacher und natürlicher den Endpunkt des ersten mit dem Anfangspunkt des zweiten gleichzusetzen und dann die Summe zweier Integrale zu bilden, von denen eines auch noch auf der Achse y=0 verläuft.
Aber beides sind nicht "völlig verschiedene Ansätze", sie unterschieden sich im wesentlichen durch die Orientierung und Lage eines Integrationsweges.
| Zitat: |
PS: Siehe Rechnung von @gast_free. Der macht es genauso wie ich. |
Was du nicht sagst. Natürlich kann man erst
 = 2x^2 -yx + V(0,y))
und dann
 = y^2 -xy + V(x,0))
ausrechenen und dann aus beiden Gleichungen, z.B. = y^2 + V(0,0)) bestimmen. bestimmen.
Oder man berechnet einfach das eine Wegintegral
 - V(0, 0) = \int_0^x 4x \dd x + \int_0^y(2y - x)\dd y = 2x^2 -xy + y^2) |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 27. Aug 2021 15:31 Titel: DrStupid Verfasst am: 27. Aug 2021 15:31 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Das Gleichsetzen bedeutet nichts anderes, als daß du die Endpunkte der beiden (vorher beliebigen) achsenparallelen Pfade gleichsetzt. |
Warum soll das Integral einer konservativen Kraft über zwei Pfade mit gleichem Endpunkt, aber unterschiedlichen Anfangspunkten, zum selben Ergebnis führen? Mir scheint, Du hast tatsächlich nicht verstanden, was ich da mache. Also noch einmal in Prosa:
Ich habe von einer Funktion V die partiellen Ableitungen nach x und y gegeben und weiß, dass x und y voneinander unabhängig sind. Um zu V zurück zu kommen, integriere ich die beiden Ableitungen wieder und setze die Ergebnisse gleich um eine der beiden Integrationskonstanten zu eliminieren. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Aug 2021 15:43 Titel: index_razor Verfasst am: 27. Aug 2021 15:43 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Das Gleichsetzen bedeutet nichts anderes, als daß du die Endpunkte der beiden (vorher beliebigen) achsenparallelen Pfade gleichsetzt. |
Warum soll das Integral einer konservativen Kraft über zwei Pfade mit gleichem Endpunkt, aber unterschiedlichen Anfangspunkten, zum selben Ergebnis führen? |
Das hat niemand behauptet. Ich sagte die Endpunkte setzt du gleich, nicht die Integrale. Das Integral über den einen Pfad ist
 - V(0, y) = 2x^2 - yx)
das Integral über den anderen Pfad ist
 - V(x,0) = y^2 -xy)
(beide verschieden). Daraus kannst du V(x,y) bis auf die Unbekannte V(0,0) bestimmen. Das ist absolut äquivalent zu dem was du machst. Siehe das Ende meines letzten Beitrags. |
|
 |
Physik_Student
Anmeldungsdatum: 01.07.2021
Beiträge: 26
|
 Physik_Student Verfasst am: 27. Aug 2021 15:56 Titel: Re: Potential aus Kraft berechnen? Physik_Student Verfasst am: 27. Aug 2021 15:56 Titel: Re: Potential aus Kraft berechnen? |
 |
|
| Zitat: |
Beide Funktionen müssen identisch sein woraus sich die Konstante ergibt.
=y^2)
=2x^2) |
Also die Konstanten hast Du hier einfach durch Vergleichen der beiden Gleichungen ermittelt, oder? Wieso ist bei dem Ansatz von DrStupid jeweils noch eine reelle Konstante C mit dabei, wenn die Ansätze gleich sind? Und danke für den Beitrag!
Übrigens finde ich die angehende Diskussion "gut", weil man dabei immer viel lernen kann als "Laie"! |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Aug 2021 16:04 Titel: Re: Potential aus Kraft berechnen? index_razor Verfasst am: 27. Aug 2021 16:04 Titel: Re: Potential aus Kraft berechnen? |
 |
|
| Physik_Student hat Folgendes geschrieben: | | Zitat: |
Beide Funktionen müssen identisch sein woraus sich die Konstante ergibt.
=y^2)
=2x^2) |
Also die Konstanten hast Du hier einfach durch Vergleichen der beiden Gleichungen ermittelt, oder? Wieso ist bei dem Ansatz von DrStupid jeweils noch eine reelle Konstante C mit dabei, wenn die Ansätze gleich sind? |
Streng genommen stimmt die Schlußfolgerung nicht. Der Vergleich liefert nur
 = y^2 + C_{0}(0))
oder
 = 2x^2 + C_0(0))
Die (in beiden Fällen gleiche) Konstante ) bleibt unbestimmt. Ich habe oben für dieselben Konstanten die Bezeichnungen bleibt unbestimmt. Ich habe oben für dieselben Konstanten die Bezeichnungen  = C_x(y)) und und =C_y(x)) verwendet. Das macht es m.E. etwas klarer. Die verbleibende Unbekannte ist also der Wert des Potentials im Ursprung. Aber es ist natürlich erlaubt diesen Wert null zu setzen. Ich habe das ganz zu Anfang ja auch selbst getan. verwendet. Das macht es m.E. etwas klarer. Die verbleibende Unbekannte ist also der Wert des Potentials im Ursprung. Aber es ist natürlich erlaubt diesen Wert null zu setzen. Ich habe das ganz zu Anfang ja auch selbst getan. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 27. Aug 2021 16:09 Titel: DrStupid Verfasst am: 27. Aug 2021 16:09 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Das hat niemand behauptet. Ich sagte die Endpunkte setzt du gleich, nicht die Integrale. |
Du hast gesagt, "Das Gleichsetzen [der Integrale über die beiden Wege] bedeutet nichts anderes, als daß du die Endpunkte der beiden (vorher beliebigen) achsenparallelen Pfade gleichsetzt."
Das stimmt so nicht. Aus der Gleichheit der Wegintegrale folgt keine Gleichheit der Endpunkte. Das gilt nicht einmal dann, wenn die Anfangspunkte gleich wären (was hier nicht möglich ist).
Da ich nicht weiß, worauf Du wirklich hinaus willst, rate ich einfach mal:
Wenn die Endpunkte der Pfade gleich sind, dann müssen die Summen aus den Wegintegralen und den Potentialen an den jeweiligen Anfangspunkten am gemeinsamen Endpunkt gleich sein (nicht umgekehrt und nicht nur die Wegintegrale allein). Dann kann man aus den Wegintegralen die Potentialdifferenz an den Anfangspunkten berechnen.
Wenn es das ist, was Du meinst, dann klingt das natürlich unnötig kompliziert. Das liegt aber nur an den angenommenen Pfaden und Wegintegralen. Wenn Du das alles mal für einen Augeblick vergisst und nur die unbestimmten Wald-und-Wiesen-Integrale betrachtest, mit denen ich oben rechne, dann bleibt von der vermeintlichen Komplexität nichts mehr übrig. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Aug 2021 16:28 Titel: index_razor Verfasst am: 27. Aug 2021 16:28 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Das hat niemand behauptet. Ich sagte die Endpunkte setzt du gleich, nicht die Integrale. |
Du hast gesagt, "Das Gleichsetzen [der Integrale über die beiden Wege] bedeutet nichts anderes, als daß du die Endpunkte der beiden (vorher beliebigen) achsenparallelen Pfade gleichsetzt."
|
Nein, du hast vom Gleichsetzen zweier unbestimmter Integrale gesprochen, das sind
 = V(0,y) + \int(4x - y)\dd x)
und
 = V(x,0) + \int(2y - x) \dd y)
Dieses Gleichsetzen ist nichts anderes als die beiden Wegintegrale  zu berechnen, die ich oben definiert habe, und deren jeweilige Endpunkte gleichzusetzen. Und beide Rechnungen sind komplett identisch, also auch gleich einfach. Aber nicht die einfachsten. zu berechnen, die ich oben definiert habe, und deren jeweilige Endpunkte gleichzusetzen. Und beide Rechnungen sind komplett identisch, also auch gleich einfach. Aber nicht die einfachsten.
| Zitat: |
Da ich nicht weiß, worauf Du wirklich hinaus willst, rate ich einfach mal:
|
Ich wollte deiner Behauptung widersprechen, daß Wegintegrale zu kompliziert für diese Aufgabe sind und hier nicht benötigt werden. Dabei war es anscheinend nötig ein paar Mißverständnisse zu korrigieren.
| Zitat: |
Wenn es das ist, was Du meinst, dann klingt das natürlich unnötig kompliziert. Das liegt aber nur an den angenommenen Pfaden und Wegintegralen. Wenn Du das alles mal für einen Augeblick vergisst und nur die unbestimmten Wald-und-Wiesen-Integrale betrachtest, mit denen ich oben rechne, dann bleibt von der vermeintlichen Komplexität nichts mehr übrig. |
Mir ist schon klar, daß das deine Auffassung ist. Aber das sehe ich anders. Wir haben es hier mit einem Vektorfeld und dessen Potential in einem zweidimensionalen Raum zu tun. Es ist nicht klar, was das "Wald-und-Wiesenintegral" in dieser Situation überhaupt sein soll. Im Prinzip ist diese Bezeichnung nur eine Verschleierung der zugrundeliegenden Konzepte, bei denen es sich um spezielle Wegintegrale handelt, nämlich solche, die parallel zu den Achsen verlaufen. Du kannst dich natürlich auf den Standpunkt stellen, daß dieses Konzept hier ruhig verschleiert werden kann, weil die Aufgabe und Lösung so einfach ist. Aber erstens muß man es sowieso lernen und verwendet dafür am besten einfache Beispiele am Anfang. Zweitens stimmt es nicht mal. Die einfachste Lösung ergibt sich aus dem Wegintegral
 - V(0, 0) = \int_0^x 4x' \dd x' + \int_0^y (2y'-x)\dd y')
Da muß man nicht mal irgendwas gleichsetzen. Man rechnet einfach zwei "Wald-und-Wiesenintegrale" aus und addiert sie.
Zuletzt bearbeitet von index_razor am 28. Aug 2021 06:49, insgesamt einmal bearbeitet |
|
 |
Physik_Student
Anmeldungsdatum: 01.07.2021
Beiträge: 26
|
 Physik_Student Verfasst am: 27. Aug 2021 16:34 Titel: Re: Potential aus Kraft berechnen? Physik_Student Verfasst am: 27. Aug 2021 16:34 Titel: Re: Potential aus Kraft berechnen? |
 |
|
| Zitat: |
Die (in beiden Fällen gleiche) Konstante ) bleibt unbestimmt. Ich habe oben für dieselben Konstanten die Bezeichnungen bleibt unbestimmt. Ich habe oben für dieselben Konstanten die Bezeichnungen  = C_x(y)) und und =C_y(x)) verwendet. verwendet. |
Danke, das macht es klarer! Dann hätte ich dazu noch eine Frage:
Oben hast Du diese beiden Gleichungen aufgeschrieben:
=2x^2-yx+V(0,y))
=y^2-xy+V(x,0))
Daraus hast Du gefolgert:
=y^2+V(0,0))
Das bekommt man ja einfach raus, indem man in der zweiten Gleichung für x null einsetzt, oder?
Wie mache ich das jetzt, wenn mein Potential auch noch von z abhängt?
Meine Überlegung ist, ich habe 3 Gleichungen der Form:
=...+V(0,y,z))
=...+V(x,0,z))
=...+V(x,y,0))
Jetzt möchte ich V(0,y,z) bestimmen, dazu setze ich es in die 2. Gleichung ein:
=...+V(0,0,z))
und das in die dritte:
=...+V(0,0,0))
passt das so? |
|
 |
Physik_Student
Anmeldungsdatum: 01.07.2021
Beiträge: 26
|
 Physik_Student Verfasst am: 27. Aug 2021 16:38 Titel: Physik_Student Verfasst am: 27. Aug 2021 16:38 Titel: |
 |
|
| Zitat: | Die einfachste Lösung ergibt sich aus dem Wegintegral
 - V(0, 0) = \int_0^x 4x' \dd x' + \int_0^y (2y'-x)\dd y') |
Wenn ich da kurz reingrätschen darf, wieso steht im ersten Integral nur 4x' und nicht 4x'-y ? |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 27. Aug 2021 16:49 Titel: DrStupid Verfasst am: 27. Aug 2021 16:49 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Nein, du hast vom Gleichsetzen zweier unbestimmter Integrale gesprochen |
Das liest sich hier aber anders:
| index_razor hat Folgendes geschrieben: |
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Genau deshalb kann ich sie ja zu einem Pfad zusammensetzen und somit das ganze Argument vereinfachen. |
Wenn Du glaubst, dass das dann noch meinem Ansatz entspricht, dann hast Du ihn nicht verstanden. Ist Dir aufgefallen, dass ich die Integrale über die beiden Wege nicht addiere, sondern gleich setze?
|
Ja, ist mir aufgefallen. Das ist ja gerade die vollkommen unnötige Komplikation. Das Gleichsetzen bedeutet nichts anderes, als daß du die Endpunkte der beiden (vorher beliebigen) achsenparallelen Pfade gleichsetzt. |
(Hervorhebung von mir.)
Dass es sich um Wegintegrale handelt, war Deine Idee:
| index_razor hat Folgendes geschrieben: | | Deine Rechnung benutzt auch zwei Pfade in der x-y-Ebene. Das scheint dir gar nicht klar zu sein. |
Und hier bestätigst Du das noch mal:
| index_razor hat Folgendes geschrieben: | | Im Prinzip ist diese Bezeichnung nur eine Verschleierung der zugrundeliegenden Konzepte, bei denen es sich um spezielle Wegintegrale handelt, nämlich solche, die parallel zu den Achsen verlaufen. |
Die Gleichheit dieser "speziellen Wegintegrale" ist nicht gleichbedeutend mit der Gleichheit der Endpunkte. Deine Meinung, dass sie hier überhaupt nötig sind, nehme ich zur Kenntnis, aber ich teile sie nicht. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Aug 2021 16:54 Titel: Re: Potential aus Kraft berechnen? index_razor Verfasst am: 27. Aug 2021 16:54 Titel: Re: Potential aus Kraft berechnen? |
 |
|
| Physik_Student hat Folgendes geschrieben: | | Zitat: |
Die (in beiden Fällen gleiche) Konstante ) bleibt unbestimmt. Ich habe oben für dieselben Konstanten die Bezeichnungen bleibt unbestimmt. Ich habe oben für dieselben Konstanten die Bezeichnungen  = C_x(y)) und und =C_y(x)) verwendet. verwendet. |
Danke, das macht es klarer! Dann hätte ich dazu noch eine Frage:
Oben hast Du diese beiden Gleichungen aufgeschrieben:
=2x^2-yx+V(0,y))
=y^2-xy+V(x,0))
Daraus hast Du gefolgert:
=y^2+V(0,0))
Das bekommt man ja einfach raus, indem man in der zweiten Gleichung für x null einsetzt, oder?
|
Genau.
| Zitat: |
Wie mache ich das jetzt, wenn mein Potential auch noch von z abhängt?
|
In diesem Fall versuchst du erstmal die ursprüngliche Strategie und verwendest gerade Strecken  = P_0 + t(P - P_0)) wenn das Gebiet sternförmig ist. Das ist in diesem Fall nämlich vermutlich am einfachsten. Die andere Strategie wird immer komplizierter, je mehr Dimensionen der Raum hat. wenn das Gebiet sternförmig ist. Das ist in diesem Fall nämlich vermutlich am einfachsten. Die andere Strategie wird immer komplizierter, je mehr Dimensionen der Raum hat.
| Zitat: |
Meine Überlegung ist, ich habe 3 Gleichungen der Form:
=...+V(0,y,z))
=...+V(x,0,z))
=...+V(x,y,0))
Jetzt möchte ich V(0,y,z) bestimmen, dazu setze ich es in die 2. Gleichung ein:
=...+V(0,0,z))
und das in die dritte:
=...+V(0,0,0))
passt das so? |
Ja, im Prinzip wird das funktionieren. Aber wie gesagt, ich finde es einfacher entweder auf direktem Weg von (0, 0, 0) nach (x,y,z) oder entlang der drei aufeinanderfolgenden Strecken (0, 0, 0) -> (x, 0, 0) -> (x, y, 0) -> (x, y, z) zu integrieren wenn das möglich ist und im letzten Fall die Ergebnisse zu addieren. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 27. Aug 2021 17:03 Titel: TomS Verfasst am: 27. Aug 2021 17:03 Titel: |
 |
|
Wenn die einfachste Lösung gesucht ist, aus der man für die Zukunft garantiert nichts lernt, dann verwendet man einfach einen Polynomansatz für V(x,y), berechnet den Gradienten und löst durch Hinschauen.
Die Methode über die Berechnung von Wegintegralen sollte man jedoch beherrschen, und daher ist es sinnvoll, sie bei dieser Aufgabe anzuwenden. Wenn die Aufgabe mittels Integration gelöst wird, dann immer mittels Wegintegralen; auch wenn man das nicht explizit hinschreibt, handelt es sich um ein solches. Und deswegen ist es erst recht sinnvoll, sich die Vorgehensweise klarzumachen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Aug 2021 17:10 Titel: index_razor Verfasst am: 27. Aug 2021 17:10 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Nein, du hast vom Gleichsetzen zweier unbestimmter Integrale gesprochen |
Das liest sich hier aber anders:
|
Ich weiß, du hast etwas anderes geschrieben. Aber wie du anscheinend selbst festgestellt hast, sind nicht die Wegintegrale gleich, sondern die unbestimmten Integrale an der Stelle (x,y). Ich bin also lediglich davon ausgegangen, daß du etwas sinnvolles gemeint hast.
Nochmal, das Gleichsetzen der beiden unbestimmten Integrale bei (x,y) entspricht dem Gleichsetzen der beiden Endpunkte der Wegintegrale. Das habe ich behauptet. Wenn du etwas anderes liest, dann nicht das, was ich geschrieben habe.
| Zitat: |
| index_razor hat Folgendes geschrieben: |
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Genau deshalb kann ich sie ja zu einem Pfad zusammensetzen und somit das ganze Argument vereinfachen. |
Wenn Du glaubst, dass das dann noch meinem Ansatz entspricht, dann hast Du ihn nicht verstanden. Ist Dir aufgefallen, dass ich die Integrale über die beiden Wege nicht addiere, sondern gleich setze?
|
Ja, ist mir aufgefallen. Das ist ja gerade die vollkommen unnötige Komplikation. Das Gleichsetzen bedeutet nichts anderes, als daß du die Endpunkte der beiden (vorher beliebigen) achsenparallelen Pfade gleichsetzt. |
(Hervorhebung von mir.)
Dass es sich um Wegintegrale handelt, war Deine Idee:
|
Nein, "meine Idee" war lediglich, daß sich deine unbestimmten Integrale mittels spezieller Wegintegrale ausdrücken lassen, nämlich in der Form
V(x,y) - V(0, y) = Wegintegral parallel zur x-Achse.
Das ist absolut trivial, wenn man verstanden hat, daß ein "unbestimmtes Integral" nichts anderes als die Klasse der Stammfunktionen ist. Deswegen hätte ich diese Erkenntnis auch gar nicht als "meine Idee" bezeichnet.
Und in dem hervorgehobenen Zitat sprichst du doch selbst davon "Integrale über die beiden Wege" gleichzusetzen. Was willst du mir also sagen? Daß du mit "Integrale über die beiden Wege" verwirrenderweise etwas anderes als Wegintegrale meinst? Das war mir ja bereits klar.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Deine Rechnung benutzt auch zwei Pfade in der x-y-Ebene. Das scheint dir gar nicht klar zu sein. |
Und hier bestätigst Du das noch mal:
| index_razor hat Folgendes geschrieben: | | Im Prinzip ist diese Bezeichnung nur eine Verschleierung der zugrundeliegenden Konzepte, bei denen es sich um spezielle Wegintegrale handelt, nämlich solche, die parallel zu den Achsen verlaufen. |
Die Gleichheit dieser "speziellen Wegintegrale" ist nicht gleichbedeutend mit der Gleichheit der Endpunkte. |
Es gibt einen einfachen Zusammenhang zwischen jedem deiner unbestimmten Integrale und einem speziellen Wegintegral über F. Der Zusammenhang erschien mir so trivial, daß ich mich zu der Behauptung hinreißen ließ, es sei "nichts anderes". Es tut mir leid, wenn ich dich damit verwirrt habe.
Zuletzt bearbeitet von index_razor am 27. Aug 2021 18:15, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Aug 2021 17:16 Titel: index_razor Verfasst am: 27. Aug 2021 17:16 Titel: |
 |
|
| Physik_Student hat Folgendes geschrieben: | | Zitat: | Die einfachste Lösung ergibt sich aus dem Wegintegral
 - V(0, 0) = \int_0^x 4x' \dd x' + \int_0^y (2y'-x)\dd y') |
Wenn ich da kurz reingrätschen darf, wieso steht im ersten Integral nur 4x' und nicht 4x'-y ? |
Man integriert ja entlang der beiden Teilstrecken (0, 0) -> (x, 0) -> (x,y).
Das Wegintegral entlang der ersten Strecke ergibt
 - V(0, 0) = \int_0^x \vec{F}(x', 0)\cdot\vec{e}_x \dd x')
d.h. im Integranden steht die x-Komponente von F auf einem beliebigen Punkt der x-Achse, d.h. bei y=0. Das zweite Integral ist dann
 - V(x, 0) = \int_0^y \vec{F}(x, y')\cdot\vec{e}_y\dd y')
und beginnt da wo das erste aufhört, nämlich bei (x, 0). Wenn man beides ineinander einsetzt, erhält man genau die obige Summe von Integralen. |
|
 |
Physik_Student
Anmeldungsdatum: 01.07.2021
Beiträge: 26
|
 Physik_Student Verfasst am: 27. Aug 2021 17:26 Titel: Re: Potential aus Kraft berechnen? Physik_Student Verfasst am: 27. Aug 2021 17:26 Titel: Re: Potential aus Kraft berechnen? |
 |
|
| Zitat: |
Ja, im Prinzip wird das funktionieren. Aber wie gesagt, ich finde es einfacher entweder auf direktem Weg von (0, 0, 0) nach (x,y,z) oder entlang der drei aufeinanderfolgenden Strecken (0, 0, 0) -> (x, 0, 0) -> (x, y, 0) -> (x, y, z) zu integrieren wenn das möglich ist und im letzten Fall die Ergebnisse zu addieren. |
Ja, das finde ich auch einfacher. |
|
 |
Physik_Student
Anmeldungsdatum: 01.07.2021
Beiträge: 26
|
 Physik_Student Verfasst am: 27. Aug 2021 17:34 Titel: Physik_Student Verfasst am: 27. Aug 2021 17:34 Titel: |
 |
|
| Zitat: |
Man integriert ja entlang der beiden Teilstrecken (0, 0) -> (x, 0) -> (x,y).
Das Wegintegral entlang der ersten Strecke ergibt
 - V(0, 0) = \int_0^x \vec{F}(x', 0)\cdot\vec{e}_x \dd x')
d.h. im Integranden steht die x-Komponente von F auf einem beliebigen Punkt der x-Achse, d.h. bei y=0. Das zweite Integral ist dann
 - V(x, 0) = \int_0^y \vec{F}(x, y')\cdot\vec{e}_y\dd y')
und beginnt da wo das erste aufhört, nämlich bei (x, 0). Wenn man beides ineinander einsetzt, erhält man genau die obige Summe von Integralen. |
Danke, jetzt verstehe ich das.
Eine Frage hätte ich noch:
Sagen wir, es wäre ein Weg vorgegeben (z.B. ein Teilchen wird von A nach B auf einer Schraubenlinie bewegt), dann müsste ich den Weg parametrisieren, z.B. mit einem Winkel und darüber integrieren, oder? Also ich kann dann nicht mehr stupide nach x,y,z integrieren, oder? Da würde die Vorgehensweise von DrStupid auch nichts dran ändern, ich müsste auch hier die Wege parametrisieren, nur dass ich es hier einzeln machen und am Ende addieren würde, richtig? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Aug 2021 17:49 Titel: index_razor Verfasst am: 27. Aug 2021 17:49 Titel: |
 |
|
| Physik_Student hat Folgendes geschrieben: | | Zitat: |
Man integriert ja entlang der beiden Teilstrecken (0, 0) -> (x, 0) -> (x,y).
Das Wegintegral entlang der ersten Strecke ergibt
 - V(0, 0) = \int_0^x \vec{F}(x', 0)\cdot\vec{e}_x \dd x')
d.h. im Integranden steht die x-Komponente von F auf einem beliebigen Punkt der x-Achse, d.h. bei y=0. Das zweite Integral ist dann
 - V(x, 0) = \int_0^y \vec{F}(x, y')\cdot\vec{e}_y\dd y')
und beginnt da wo das erste aufhört, nämlich bei (x, 0). Wenn man beides ineinander einsetzt, erhält man genau die obige Summe von Integralen. |
Danke, jetzt verstehe ich das.
Eine Frage hätte ich noch:
Sagen wir, es wäre ein Weg vorgegeben (z.B. ein Teilchen wird von A nach B auf einer Schraubenlinie bewegt), dann müsste ich den Weg parametrisieren, z.B. mit einem Winkel und darüber integrieren, oder? Also ich kann dann nicht mehr stupide nach x,y,z integrieren, oder?
|
Also wenn das Vektorfeld ein Potential besitzt, dann ist es ja gerade egal welchen Weg du nimmst. Das Ergebnis ist in jedem Fall
 - V(A))
was selbstverständlich am einfachsten zu berechnen ist, wenn man V schon kennt. Wenn die Aufgabe also nicht explizit verlangt, genau dieses Wegintegral entlang der Schraubenlinie auszurechnen, dann mußt du das auch nicht tun.
| Zitat: |
Da würde die Vorgehensweise von DrStupid auch nichts dran ändern, ich müsste auch hier die Wege parametrisieren, nur dass ich es hier einzeln machen und am Ende addieren würde, richtig? |
DrStupids Methode diente ja nur zur Bestimmung eines Potentials. Erst das Potential zu bestimmen, kann natürlich prinzipiell einfacher sein, als das Integral entlang irgendeines komplizierten Weges zu berechnen. Denn komplizierter als Integrale entlang von Geraden kann die Bestimmung von V eigentlich kaum werden. Integrale über Schraubenlinien können je nach F aber sicher beliebig kompliziert werden.
EDIT: Andererseits, Integrale über Geraden sind eventuell auch nicht unbedingt die einfachsten. Es hängt natürlich schon von F ab. Aber immerhin hat man bei Potentialfeldern die Möglichkeit nach dem einfachsten Integrationsweg zu suchen und daraus V zu bestimmen. Dann werden alle anderen Wegintegrale trivial. |
|
 |
|
|















