| Autor |
Nachricht |
Systemdynamiker
Anmeldungsdatum: 22.10.2008
Beiträge: 594
Wohnort: Flurlingen
|
 Systemdynamiker Verfasst am: 06. Jun 2018 09:41 Titel: Trägheitsgesetz Systemdynamiker Verfasst am: 06. Jun 2018 09:41 Titel: Trägheitsgesetz |
 |
|
Zurzeit plane ich ein Video zum 1. Newtonschen Gesetz. Dabei geht es um die Frage, ob das 1. Gesetz ein Spezialfall des 2. ist oder eine unabhängige, eigenständige Aussage beinhaltet.
Die Unabhängigkeits-Fraktion, zu der auch namhafte Theoretiker gehören, sieht im Trägheitsgesetz die Begründung des Inertialsystems. Ich sehe da ein grosses Problem. Newton hat Raum und Zeit ohne Begründung (a priori) eingeführt. Das 2. Newtonsche Gesetz gilt damit in allen zum absoluten Raum gleichförmig bewegten Bezugssytemen. Solche Systeme nennt man in der Newtonsche Mechanik Inertialsysteme. Eine Begründung in Form des Trägheitsgesetzes ist damit überflüssig.
In der Relativitätstheorie äussert sich die Gravitation in der Metrik der Raumzeit. Folglich bezieht sich kräftefrei auf alle Kräfte ausser der Gravitation und jedes frei fallende System (z.B. die ISS) ist lokal ein Indertialsystem.
_________________
Herzliche Grüsse Werner Maurer |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 06. Jun 2018 21:28 Titel: VeryApe Verfasst am: 06. Jun 2018 21:28 Titel: |
 |
|
wie kann denn das Trägheitsgesetz überflüssig sein, wenn man anhand des zweiten Axioms nur erkennt das die Kraft eine Bewegungsänderung hervorfuhrt eine Beschleunigung, eine veränderung der Geschwindigkeit und die wiederum eine Veränderung des Weges aber welchen Weges.
krumme Bahnen? geradlinige Bahnen. 
Aber was fang ich damit an wenn ich nicht weiß auf welche Koordinaten ich die Beschleunigung beziehen soll, da steht doch im ersten Axiom bewegt sich geradlinig unter Trägheit.
also brauche ich kartesische Koordinaten.
Ohne den Zusatz wie weiß ich dann auf welche Koordinaten ich mich beziehen soll.
Absoluter Raum schön und gut und wie beschreib ich den mit welchen Koordinaten? damit ich das zweite Axiom anwenden kann.?
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
Systemdynamiker
Anmeldungsdatum: 22.10.2008
Beiträge: 594
Wohnort: Flurlingen
|
 Systemdynamiker Verfasst am: 07. Jun 2018 17:46 Titel: Polarkoordinaten Systemdynamiker Verfasst am: 07. Jun 2018 17:46 Titel: Polarkoordinaten |
 |
|
Nehmen wir zwei Himmelskörper im sonst weitherum leeren Raum. Nun legen wir das Koordinatensystem in den Schwerpunkt dieses Zweikörperproblems und führe Polarkoordinaten (Zylinderkoordinaten) ein. Selbstverständlich gilt das 2. Newtonsche Gesetz für beide Himmelskörper. Die Beschleunigung muss man halt in Polarkoordinaten ausdrücken.
Begeben wir uns nun in die ISS. Ein schwebender Körper bleibt in Ruhe, ein angestossener Körper bewegt sich geradlinig bis zur Wand. Ist die ISS ein Inertialsystem. Aus der Sicht der Newtonschen Mechanik sicher nicht. Die ISS fällt beschleunigt um die Erde und zusammen mit dieser um die Sonne. Die Sonne bewegt sich beschleunigt innerhalb der Milchstrasse. Die Unmöglichkeit, die Gewichtskraft direkt zu messen, hindert uns daran, Kräftefreiheit (mit Einbezug der Gravitation) festzustellen. Ohne Kräftefreiheit kein 1. Newtonsches Gesetz.
_________________
Herzliche Grüsse Werner Maurer |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 07. Jun 2018 18:12 Titel: Re: Polarkoordinaten index_razor Verfasst am: 07. Jun 2018 18:12 Titel: Re: Polarkoordinaten |
 |
|
| Systemdynamiker hat Folgendes geschrieben: |
Begeben wir uns nun in die ISS. Ein schwebender Körper bleibt in Ruhe, ein angestossener Körper bewegt sich geradlinig bis zur Wand. Ist die ISS ein Inertialsystem. Aus der Sicht der Newtonschen Mechanik sicher nicht. Die ISS fällt beschleunigt um die Erde und zusammen mit dieser um die Sonne. Die Sonne bewegt sich beschleunigt innerhalb der Milchstrasse. Die Unmöglichkeit, die Gewichtskraft direkt zu messen, hindert uns daran, Kräftefreiheit (mit Einbezug der Gravitation) festzustellen. Ohne Kräftefreiheit kein 1. Newtonsches Gesetz. |
Die Auffassung des Äquivalenzprinzips, nach der
(unbeschleunigte) Trägheitsbewegung = freier Fall
kann man auch in der Newtonschen Mechanik erfüllen. Das Ergebnis ist eine gekrümmte Newtonsche Raumzeit. Einige würden diese Theorie nicht mehr als "Newtonsche Mechanik" bezeichnen, aber das halte ich für unbegründet. Es handelt sich lediglich um eine kovariante Formulierung derselben Theorie. Das sieht man sofort an der Form der Geodätengleichung in lokalen Inertialsystemen. Diese lautet

wobei 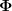 das lokale Gravitationspotetial und die Ableitung nach der absoluten Zeit zu nehmen ist. Es handelt sich also um exakt dieselbe Bewegungsgleichung, wie in der Standardformulierung mit globalen Inertialsystemen. Nur benötigt man solche Inertialsysteme nicht mehr als Basis zur Formulierung der Theorie. das lokale Gravitationspotetial und die Ableitung nach der absoluten Zeit zu nehmen ist. Es handelt sich also um exakt dieselbe Bewegungsgleichung, wie in der Standardformulierung mit globalen Inertialsystemen. Nur benötigt man solche Inertialsysteme nicht mehr als Basis zur Formulierung der Theorie.
Das ganze ist auch als Newton-Cartan-Theorie bekannt. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 07. Jun 2018 21:01 Titel: VeryApe Verfasst am: 07. Jun 2018 21:01 Titel: |
 |
|
| Zitat: |
Nehmen wir zwei Himmelskörper im sonst weitherum leeren Raum. Nun legen wir das Koordinatensystem in den Schwerpunkt dieses Zweikörperproblems und führe Polarkoordinaten (Zylinderkoordinaten) ein. Selbstverständlich gilt das 2. Newtonsche Gesetz für beide Himmelskörper. Die Beschleunigung muss man halt in Polarkoordinaten ausdrücken.
|
Angenommen die 2 Himmelskörper haben selbe Masse m und kreisen auf einer Kreisbahn r genau gegenüber liegend mit gleicher Winkelgeschwindigkeit.
Gehe ich da jetzt in den Massenmittelpunkt der genau in Kreismittelpunkt liegt und nehme Zylinderkoordinaten.
dann wäre

und

und deren zweite Ableitungen (Beschleunigungen) =null, beziehe ich Beschleunigung auf dieses Koordinatensystem wird doch gar nicht beschleunigt und die Kraft ist null.
Gallilei kannte auch schon das Trägheitsgesetz und soweit ich weiß glaubte er das die Kugeln zwar von selbst aufgrund der Trägheit in Bewegung bleiben aber er dachte sie würden entlang der Erdoberfläche bewegen aufgrund der Trägheit.
Das heißt sie würden um die Erde herumrollen auf Kreisbahnen ohne Kräfte.
Weiß nicht Newton und Descartes waren es dann die gesagt haben nein die Trägheitsbewegung geht geradlinig.
und damit würde man dann bei kartesischen Koordinaten auf v²/r kommen und mit dem 2 Axiom auf das wirken von Kräften.
vielleicht sehe ich da was nicht richtig.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
Systemdynamiker
Anmeldungsdatum: 22.10.2008
Beiträge: 594
Wohnort: Flurlingen
|
 Systemdynamiker Verfasst am: 08. Jun 2018 11:36 Titel: Unabhängigkeit Systemdynamiker Verfasst am: 08. Jun 2018 11:36 Titel: Unabhängigkeit |
 |
|
Eine Geometrisierung im Sinne der Newton-Cartan-Theorie beantwortet diese Frage nicht, weil damit wie in der AR die Gewichtskraft als solche zugunsten einer geometrischen Wirkung abgeschafft wird.
Wie die Beschleunigung in Polarkoordinaten formuliert wird, ist in diesem Forum schon behandelt worden https://www.physikerboard.de/topic,26383,-beschleunigung-in-polarkoordinaten.html Die Wahl der Koordinaten darf keinen Einfluss auf die Gesetze haben.
Ich vermute, dass Newton das erste Gesetz als Antwort auf Aristoteles und als Referenz an Galiei aufgestellt hat. Im Unterricht führt man dieses Gesetz ein, damit die Auszubildenden begreifen, was ein kräftefreier Körper im Gegensatz zur Alltagsvorstellung macht. Rei logisch erscheint mir das erste Gesetz immer noch ein Spezialfall des zweiten zu sein.
Die Gewichtskraft und damit auch der Problemkreis der Trägheitskräfte ist in vielen Lehrbüchern oft ein Schwachpunkt. Solange man nicht zwischen unmittelbar messbaren Oberflächenkräften (Hookesches Gesetz) und nicht direkt messbarer, am ganzen Volumen angreifenden Gewichtskraft unterscheidet, bleiben die Newtonschen Gesetze nicht greifbar (siehe z.B. https://de.wikipedia.org/wiki/Schiefe_Ebene Versionsgeschichte).
_________________
Herzliche Grüsse Werner Maurer |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Jun 2018 12:49 Titel: index_razor Verfasst am: 08. Jun 2018 12:49 Titel: |
 |
|
| Systemdynamiker hat Folgendes geschrieben: | Eine Geometrisierung im Sinne der Newton-Cartan-Theorie beantwortet diese Frage nicht, weil damit wie in der AR die Gewichtskraft als solche zugunsten einer geometrischen Wirkung abgeschafft wird.
|
Welche Frage wird nicht beantwortet? Ob das 1. Axiom ein Spezialfall des 2. ist? Das stimmt. Es sollte auch nur die Frage beantworten, was Kräftefreiheit in der Newtonschen Mechanik bei Anwesenheit von Gravitation bedeutet.
Die Geometrisierung löst auch das Problem, ob die Bewegungsgleichungen nur in bestimmten ausgezeichneten Systemen gelten, die man vorher irgendwie unabhängig von der Dynamik definieren muß. Das kann m.E., wenn man sich zum ersten Mal mit den theoretischen Grundlagen der Mechanik beschäftigt, eine ziemlich harte Nuß sein. (Welchen Status die Trägheitskräfte innerhalb der Theorie haben, spielt in diesem Zusammenhang auch eine Rolle.) Die Antwort lautet "Nein, die Axiome der Mechanik sind, wie alle Naturgesetze, bezugssystemunabhängige Aussagen."
Die Frage nach der Unabhängigkeit der beiden Axiome, läßt sich innerhalb dieser Diskussion hier m.E. noch nicht klar beantworten, weil sie nicht präzise genug definiert sind. Wenn man ungefähr folgendes formuliert
2 Axiom: Für alle Teilchen existiert ein 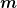 und ein und ein ) , so daß für Bahnkurve x(t) der Teilchen gilt , so daß für Bahnkurve x(t) der Teilchen gilt
)
und
1. Axiom: Wenn 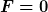 , dann ist , dann ist 
ist wohl klar, daß es sich beim ersten Axiom um eine triviale Folgerung des 2. handelt, ohne, daß man noch lange herumphilosophieren muß.
Für mich ist der Kern des 1. Axioms allerdings eher der, zu definieren, was  überhaupt bezugssystemunabhängig bedeutet. Damit sind wir wieder bei der kovarianten Formulierung. überhaupt bezugssystemunabhängig bedeutet. Damit sind wir wieder bei der kovarianten Formulierung.
| Zitat: |
Die Gewichtskraft und damit auch der Problemkreis der Trägheitskräfte ist in vielen Lehrbüchern oft ein Schwachpunkt. Solange man nicht zwischen unmittelbar messbaren Oberflächenkräften (Hookesches Gesetz) und nicht direkt messbarer, am ganzen Volumen angreifenden Gewichtskraft unterscheidet, bleiben die Newtonschen Gesetze nicht greifbar (siehe z.B. https://de.wikipedia.org/wiki/Schiefe_Ebene Versionsgeschichte). |
Hier bin ich abgehängt. Ich stimme dir zu, daß die Diskussion von Trägheitskräften oft nicht optimal ist. Was eine Unterscheidung zwischen Oberflächenkräften und Volumenkräften hier bringen soll (und wieso ist das Hooksche Gesetz überhaupt eine "Oberflächenkraft"?), ist mir aber nicht klar.
Das besondere an der Gewichtskraft ist nicht, daß es sich um eine Volumenkraft handelt, sondern, daß sie, im Gegensatz zu allen anderen Wehselwirkungskräften, das Äquivalenzprinzip erfüllt. Nach gängiger Auffassung ist sie damit proportional zur Masse, die sie beeinflußt. Das rückt sie ein Schritt näher an die "Trägheitskräfte", für die dasselbe gilt.
Die Konsequenz ist, daß die Wirkung der Gravitationskraft auf alle Testteilchen von sämtlichen inneren Teilcheneigenschaften unabhängig ist, d.h. die Bahnkurve dieser Teilchen hängt nur von deren anfänglichem Ort und Geschwindigkeit ab. Diese vollkommene Unabhängigkeit von den individuellen Eigentümlichkeiten der Teilchen, macht deren Kurven zu geometrischen Eigenschaften der Raumzeit. Man muß nur konsequent zuende denken, daß es genau diese Kurven sind, von denen das erste Axiom spricht. Ich wüßte nicht, was daran "nicht greifbar" bleiben sollte. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Jun 2018 18:22 Titel: index_razor Verfasst am: 08. Jun 2018 18:22 Titel: |
 |
|
Hierauf wollte ich auch noch eingehen:
| Systemdynamiker hat Folgendes geschrieben: |
Die Unabhängigkeits-Fraktion, zu der auch namhafte Theoretiker gehören, sieht im Trägheitsgesetz die Begründung des Inertialsystems. Ich sehe da ein grosses Problem. Newton hat Raum und Zeit ohne Begründung (a priori) eingeführt. Das 2. Newtonsche Gesetz gilt damit in allen zum absoluten Raum gleichförmig bewegten Bezugssytemen. Solche Systeme nennt man in der Newtonsche Mechanik Inertialsysteme. Eine Begründung in Form des Trägheitsgesetzes ist damit überflüssig.
|
Wie definierst du denn, was geradlinig-gleichförmig "in Bezug auf den absoluten Raum" ist? Deiner Formulierung entnehme ich, daß du hier von einer absoluten Bewegung gegenüber dem Raum sprichst. Wenn nicht, benötigst du irgendein "Prinzip", welches dir die theoretischen Begriffe liefert um Trägheitsbewegungen festzustellen bzw. zu definieren. Dieses Prinzip, wie auch immer du es formulierst, kannst du dann als "1. Axiom" bezeichnen.
(Es stellt sich heraus, daß der benötigte Begriff genau ein affiner torsionsfreie Zusammenhang ist, der die euklidische Struktur des absoluten Raumes respektiert. Ein affiner Zusammenhang definiert "Geradlinigkeit" in der Geometrie. Warum also eine Aussage, die seine Existenz fordert nicht als "Trägheitsprinzip" bezeichnen, welches ja genau von Geradlinigkeit in Raum und Zeit spricht?)
Eine absolute Bewegung gegen den Raum wäre hingegen eine theoretische Fiktion, die mit dem Relativitätsprinzip in Konflikt steht. Selbst wenn diese absolute Bewegung durch die Symmetrien der Bewegungsgleichung unbeobachtbar wird, bleibt die Frage warum man sie in die Grundkonzepte der Theorie einführen sollte. Auf Grund ähnlicher Vorbehalte bevorzugen wir ja auch die spezielle Relativitätstheorie gegenüber der Lorentzschen Äthertheorie, obwohl in dieser die Bewegung gegenüber dem Äther genauso unbeobachtbar ist wie in jener.
Alles was wir über die Struktur der Raumzeit wissen, wissen wir aus den dynamischen Gleichungen, deren Effekte wir beobachten. Wir sollten also annehmen, daß deren Symmetrien in der Struktur der Raumzeit widergespiegelt sind, solange wir nicht zum Gegenteil gezwungen sind. (Genau diese Überlegungen haben ja auch zur speziellen Relativitätstheorie geführt.) In der Newtonschen Theorie haben wir es zwar mit einem absoluten Raum, definiert durch "absolute Zeit = t = const." zu tun. Es existiert aber auf Grund des Relativitätsprinzips keine beobachterunabhängige Definition von "Gleichortigkeit" von Ereignissen zu verschiedenen Zeitpunkten. Also gibt es auch keinen Begriff von absoluter Bewegung im Raum. Somit liefert dir der absolute Raum allein auch noch keine Definition von "Trägheitsbewegung". |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 09. Jun 2018 10:03 Titel: TomS Verfasst am: 09. Jun 2018 10:03 Titel: |
 |
|
Über welche Formulierung der Newtonschen Axiome reden wir eigentlich? Und an welcher Stelle soll der Begriff des Inertialsystems eingeführt werden? Nur in einem Inertialsystem bewegen sich kräftefreie Körper geradlinig gleichförmig. Oder reden wir auch von Scheinkräften? An welcher Stelle soll dieser Begriff eingeführt werden?
M.E. sind diese Voraussetzungen zu klären, bevor man weiter diskutieren kann.
Ansonsten s.o.: setzt man die Verwendung von Inertialsystemen voraus, dann ist Newton I eine Konsequenz aus Newton II.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 09. Jun 2018 10:56 Titel: index_razor Verfasst am: 09. Jun 2018 10:56 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Über welche Formulierung der Newtonschen Axiome reden wir eigentlich? Und an welcher Stelle soll der Begriff des Inertialsystems eingeführt werden? Nur in einem Inertialsystem bewegen sich kräftefreie Körper geradlinig gleichförmig.
|
Oder -- kovariante Formulierung --
Nur in einem Inertialsystem bedeutet "geradlinig-gleichförmig" dasselbe wie

Allgemein bedeutet es systemunabhängig
 = \ddot x^i e_i + \dot x^i \frac{\nabla}{\dd t}e_i)
Im zweiten Term findet man für

die Scheinkräfte wieder.
Man kann sich natürlich auch von vornherein auf Bezugssysteme stürzen. Dann würde ich das 1. Axiom als Existenzaussage für Inertiasysteme formulieren
1. Axiom: Es existiert ein Bezugssystem, in dem ein kräftefreier Körper den Bewegungsgleichungen 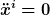 gehorcht. gehorcht.
Und das 2. Axiom mit bezug auf diese Inertialsysteme als Existenzaussage über das Kraftgesetz (und die Masse)
2. Axiom: Für jedes Teilchen mit Masse m existiert ein F(x,x',t), so daß die Wechselwirkung mit anderen Teilchen im Inertialsystem durch die Bewegungsggleichung
)
beschreibbar ist. Dann ist das 1. Axiom keine Folge aus dem zweiten, sondern das zweite beruht auf dem ersten. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 09. Jun 2018 11:44 Titel: TomS Verfasst am: 09. Jun 2018 11:44 Titel: |
 |
|
Ist das nicht zirkulär?
| index_razor hat Folgendes geschrieben: | Dann würde ich das 1. Axiom als Existenzaussage für Inertiasysteme formulieren
1. Axiom: Es existiert ein Bezugssystem, in dem ein kräftefreier Körper den Bewegungsgleichungen 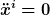 gehorcht. gehorcht.
|
Was bedeutet hier kräftefrei?
Das ist für die Gravitationskraft ein Problem, denn bzgl. der flachen, absoluten Newtonschen Raumzeit bewegt sich ein kräftefreier = frei fallender Körper, der sich so bewegt, dass er selbst keine Kraft spürt bzw. für den ein mitbewegter Beobachter auf der Federwaage keine Kraft misst eben gerade nicht geradlinig gleichförmig (sondern z.B. sondern auf Ellipsen oder Hyperbeln).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 09. Jun 2018 17:03 Titel: index_razor Verfasst am: 09. Jun 2018 17:03 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Ist das nicht zirkulär? |
Ich denke schon. Welche Formulierung wäre denn nicht zirkulär?
Ich sehe die Axiome nicht als explizite Definitionen, sondern als Aussagen, die die Beziehung der Grundbegriffe zueinander klären. Das bedeutet jeder dieser Begriffe nimmt irgendwie Bezug zu allen anderen. Das definiert sie höchstens auf recht implizite Weise. Aber anders kann es doch aus logischen Gründen gar nicht funktionieren. Die einzige Alternative wäre ein unendlicher Regress.
Der Kraftbegriff ist für mich tatsächlich auch derjenige, der hier am schwammigsten bleibt. Aber das ist auch gerechtfertigt: In der Praxis, bzw. den Anwendungsfällen der Theorie, konkretisieren den Begriff ja erst durch Angabe eines konkreten Kraftgesetzes. Ohne Kenntnis eines oder besser ganz vieler solche Kraftgesetze kann man nicht viel mehr machen, als darauf zu verweisen, daß eine "Kraft" auf ein Teilchen irgendetwas mit der Wechselwirkung mit anderen Teilchen zu tun hat und versuchen die Bedingung für Kräftefreiheit zu realisieren, indem man den Körper möglichst weit von anderen isoliert.
Damit hat immerhin schon mal eine Arbeitshypothese in Form einer hinreichenden Bedingung für "kräftefrei", wenn auch keine formale Definition.
| Zitat: |
| index_razor hat Folgendes geschrieben: | Dann würde ich das 1. Axiom als Existenzaussage für Inertiasysteme formulieren
1. Axiom: Es existiert ein Bezugssystem, in dem ein kräftefreier Körper den Bewegungsgleichungen 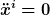 gehorcht. gehorcht.
|
Was bedeutet hier kräftefrei?
Das ist für die Gravitationskraft ein Problem, denn bzgl. der flachen, absoluten Newtonschen Raumzeit bewegt sich ein kräftefreier = frei fallender Körper, der sich so bewegt, dass er selbst keine Kraft spürt bzw. für den ein mitbewegter Beobachter auf der Federwaage keine Kraft misst eben gerade nicht geradlinig gleichförmig (sondern z.B. sondern auf Ellipsen oder Hyperbeln). |
Das hatten wir glaube ich schon mal diskutiert: Wenn du "kräftefrei" mit "frei fallend" identifizierst, dann ist die Newtonsche Raumzeit eben nicht mehr flach, sondern gekrümmt. Dir Krümmung wird durch die lokale Massendichte bestimmt

Nur der absolute Raum ist immer flach. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 09. Jun 2018 17:47 Titel: Re: Trägheitsgesetz DrStupid Verfasst am: 09. Jun 2018 17:47 Titel: Re: Trägheitsgesetz |
 |
|
| Systemdynamiker hat Folgendes geschrieben: | | Dabei geht es um die Frage, ob das 1. Gesetz ein Spezialfall des 2. ist oder eine unabhängige, eigenständige Aussage beinhaltet. |
Das erste Axiom definiert die Kraft als (einzige) Ursache von Bewegungsänderungen. Das geht aus dem zweiten Axiom nicht hervor. Welchen praktischen Nutzen diese Festlegung hat, ist eine andere Frage.
| Systemdynamiker hat Folgendes geschrieben: | | Die Unabhängigkeits-Fraktion, zu der auch namhafte Theoretiker gehören, sieht im Trägheitsgesetz die Begründung des Inertialsystems. |
Inertialsysteme werden durch das dritte Axiom begündet. Die ersten beiden würden ohne das dritte auch in Nicht-Inertialsystemen gelten, weil es dann keinen Unterschied zwischen Wechselwirkungs- und Trägheitskräften gäbe. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 09. Jun 2018 19:01 Titel: VeryApe Verfasst am: 09. Jun 2018 19:01 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Über welche Formulierung der Newtonschen Axiome reden wir eigentlich? |
Ich dachte von diesen hier.
| Isaac Newton, Grundsätze der Bewegung hat Folgendes geschrieben: |
1. Gesetz. Jeder Körper beharrt in seinem Zustande der Ruhe oder der gleichförmigen geradlinigen Bewegung, wenn er nicht durch einwirkende Kräfte gezwungen wird, seinen Zustand zu ändern.
2. Gesetz. Die Aenderung der Bewegung ist der Einwirkung der bewegenden Kraft proportional und geschieht nach der Richtung derjenigen geraden Linie, nach welcher jene Kraft wirkt.
3. Gesetz. Die Wirkung ist stets der Gegenwirkung gleich, oder die Wirkungen zweier Körper auf einander sind stets gleich und von entgegengesetzter Richtung
|
Für mich stellt sich die Frage, was ist überhaupt eine Änderung der Bewegung.
wenn sich ein Körper konstant im Kreis bewegt, ändert er ja seine Kreisbewegung nicht. Ist eine Richtungsänderung alleine schon eine Bewegungsänderung?
WEnn ein Körper aufgrund der Trägheit eine krumme Linie entlang fliegt, verändert er dann seine Bewegung oder, verändert er nur seine Bewegung wenn er von dieser Kurve abweicht bzw diese Kurve aufeinmal immer schneller durchfliegt.
Und für mich schreibt Newton das im 1 Axiom Gesetz hin.
Eine Bewegungsänderung findet dann statt wenn ein Körper von einer geradenlinie abweicht oder er sich nicht gleichförmig auf diese bewegt.
und das was DrStupid zum Schluss geschrieben hat lese ich auch heraus.
Da steht nur im 2 Axiom das die Kraft eine Bewegungsänderung hervorruft aber es könnte ja auch noch irgendetwas anderes Bewegungsänderung hervorrufen.
Wenn eine Kug
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 09. Jun 2018 21:12 Titel: DrStupid Verfasst am: 09. Jun 2018 21:12 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | | Für mich stellt sich die Frage, was ist überhaupt eine Änderung der Bewegung. |
Mit "Bewegung" meint Newton den Impuls (siehe Definition 2). Das zweite Axiom bedeutet also F=dp/dt.
| VeryApe hat Folgendes geschrieben: | | Da steht nur im 2 Axiom das die Kraft eine Bewegungsänderung hervorruft |
Im zweiten Axiom steht, dass die Kraft proportional zur Bewegungsänderung ist, aber nicht, dass sie sie vervorruft. Ohne das erste Axiom könnte beides identisch sein. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 09. Jun 2018 22:04 Titel: VeryApe Verfasst am: 09. Jun 2018 22:04 Titel: |
 |
|
ja schon klar, aber dann anders was ist Geschwindigkeitsänderung.
Wussten die damals schon das die Richtungsänderung selbst wenn der Betrag gleich bleibt auch eine Änderung der Geschwindigkeit ist.
| Die Bewegungslehre des Aristoteles hat Folgendes geschrieben: |
Aristoteles (384 bis 322 v.Chr.) teilt irdische Bewegungen in zwei Klassen
ein: in "natürliche" und "erzwungene"
. Im geordneten Universum des Aris-
toteles hat jeder Körper die innere Te
ndenz, sich in natürlicher Bewegung
dem ihm zukommenden Ort zu nähern: Das Leichte strebt nach oben, das
Schwere nach unten. Aus diesem Grunde steigen Luftblasen im Wasser
nach oben und fällt ein Stein zu Boden. Im Gegensatz zu den natürlichen
Bewegungen erfordern erzwungene Bewegungen einen aktiven äußeren
Beweger, bzw. eine ständig wirkende
Kraft. Nur dadurch kann sich ein
Körper von seinem natürlichen Ort entfernen oder von einer natürlichen
Bewegung abweichen.
|
für mich klingt es so als hätten die geglaubt wenn es ein natürliches Bestreben des Körper auf einer Kreisbahn zu kreisen wäre, dann hat das auch nichts mit einer Änderung der Bewegung bzw mit einer Änderung der Geschwindigkeit zu tun und mit einer erfoderlichen Kraft umso mehr war es da doch erforderlich das Newton auf den Tisch haut und sagt erstes Gesetz Körper hat das Bestreben sich geradlinig gleichförmig zu bewegen, alles andere erfordert Kräfte.
Ich mein heute durchschauen wir alles einigermassen, die Mathematik is um vielzahl besser, aber stell wir uns mal vor wir wären da in der damaligen zeit.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 10. Jun 2018 09:24 Titel: TomS Verfasst am: 10. Jun 2018 09:24 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Über welche Formulierung der Newtonschen Axiome reden wir eigentlich? |
Ich dachte von diesen hier.
| Isaac Newton, Grundsätze der Bewegung hat Folgendes geschrieben: |
1. Gesetz. Jeder Körper beharrt in seinem Zustande der Ruhe oder der gleichförmigen geradlinigen Bewegung, wenn er nicht durch einwirkende Kräfte gezwungen wird, seinen Zustand zu ändern.
|
|
Und da ergibt sich im Falle der Gewichtskraft das Problem, dass
a) ein Körper, der auf der Erdoberfläche liegt, ist zunächst nicht kräftefrei ist - man spürt und misst die Gewichtskraft - und man muss immer mit der Gegenkraft bzw. Kräftegleichgewicht argumentieren, um zu erklären, warum dieser Körper dennoch gleichförmig geradlinigen bewegt ist - in diesem Spezialfall nämlich gar nicht.
b) ein Körper wie die ISS tatsächlich kräftefrei ist - man spürt und misst an Bord keine Kraft - jedoch dennoch nicht gleichförmigen geradlinigen bewegt ist - sondern entlang einer Ellipsenbahn.
Damit ist der pädagogische Ansatz über die Newtonschen Axiome extrem verwirrend, weil die allen Schülern gegenwärtige Gewichtskraft offensichtlich ein Problem darstellt, man jedoch kein Experiment praktisch demonstrieren kann, wo diese abwesend ist.
Siehe auch das Argument von index_razor: man kann die Kraft geeignet definieren, so dass kräftefrei gleich frei fallend ist, und dann ist auch intuitiv einleuchtend: in einer frei fallenden Achterbahn wird keine Gewichtskraft gemessen. Dann muss man jedoch zu einer mathematisch aufwändigen Formulierung greifen, in der mittels Krümmung ein anderer Begriff von „gerade“ eingeführt wird - was einen für Einführungskurse o.ä. sicher nicht weiterbringt.
Daher wäre m.E. zu überlegen, ob man nicht einen alternativen Zugang findet, der ohne die Newtonschen Axiome auskommt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 10. Jun 2018 10:28, insgesamt 4-mal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 10. Jun 2018 09:32 Titel: TomS Verfasst am: 10. Jun 2018 09:32 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Der Kraftbegriff ist für mich tatsächlich auch derjenige, der hier am schwammigsten bleibt. |
Sehe ich auch so.
| index_razor hat Folgendes geschrieben: | | Das hatten wir glaube ich schon mal diskutiert: Wenn du "kräftefrei" mit "frei fallend" identifizierst, dann ist die Newtonsche Raumzeit eben nicht mehr flach, sondern gekrümmt. |
Die Frage ist dann, ob dieser Ansatz überhaupt für eine Einführung taugt.
Und warum sollte ich - und jeder Schüler - denn nicht kräftefrei mit frei fallend identifizieren? Das ist doch genau das, was ihm eine Waage als Kraftmesser sagt.
Je mehr ich darüber nachdenke, desto eher bin ich geneigt, einen alternativen Zugang zu suchen der die Newtonschen Axiome ersetzt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 10. Jun 2018 10:39 Titel: TomS Verfasst am: 10. Jun 2018 10:39 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | Für mich stellt sich die Frage, was ist überhaupt eine Änderung der Bewegung.
wenn sich ein Körper konstant im Kreis bewegt, ändert er ja seine Kreisbewegung nicht. Ist eine Richtungsänderung alleine schon eine Bewegungsänderung?
|
Eine Kreisbewegung ist nicht geradlinig gleichförmig, und das bedeutet gem. Newton, dass eine Kraft wirkt. Das ist anschaulich klar für einen an einer Schnur herumgewirbelten Körper, oder für ein Elektron im homogenen Magnetfeld. In diesen Fällen spürt bzw. misst man auch eine Kraft auf einem Kraftmesser (jedoch nicht die eigtl. wirkende Kraft, sondern die Trägheitskraft, die der Ablenkung entgegenwirkt; dies entspricht actio = reactio).
Im Falle der Kreis- oder Ellipsenbahn eines Satelliten verhält es sich jedoch anders: man argumentiert zwar mit der Gravitationskraft, die den Satelliten auf eine Kreisbahn zwingt, jedoch spürt bzw. misst man hier keine Kraft. Man misst andererseits genau dann eine Kraft, wenn der Körper auf der Erdoberfläche in Ruhe ist und sich geradlinig gleichförmig bewegt. Der intuitive Zugang zum Kraftbegriff ist also extrem irreführend, da er für ein um die selbe Situation - ein Körper bewegt sich auf einer Kreisbahn - widersprüchliche Aussagen liefert.
Wir wissen heute natürlich, woher dieser fundamentale Unterschied rührt, nämlich aus der ART, derzufolge dir Bahn des kräftefrei bewegten Satelliten tatsächlich im verallgemeinerten Sinne der Riemannschen Geometrie gerade ist.
Das Problem dieses Zugangs über die Newtonsche Axiome ist, dass Sie diese Problematik zunächst nicht erklären können. Der Ausweg, bereits in der Newtonschen Mechanik einen gekrümmten Raum einzuführen, ist für eine Einführung nutzlos. Der Ausweg, mittels der ART zu argumentieren, ist ebenso nutzlos.
Wenn also der Zugang über die Newtonsche Axiome diese einfachen und anschaulichen Probleme nicht vernünftig erklären kann, sollte man nach einer alternativen Formulierung oder einem alternativen Zugang suchen. Das ist nicht die Fragestellung zu Beginn des Threads, aber m.E. eine zentrale Problematik im Kontext der Einfoder Newtonschen Mechanik.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 10. Jun 2018 11:48 Titel: index_razor Verfasst am: 10. Jun 2018 11:48 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
| index_razor hat Folgendes geschrieben: | | Das hatten wir glaube ich schon mal diskutiert: Wenn du "kräftefrei" mit "frei fallend" identifizierst, dann ist die Newtonsche Raumzeit eben nicht mehr flach, sondern gekrümmt. |
Die Frage ist dann, ob dieser Ansatz überhaupt für eine Einführung taugt.
|
Das schlage ich ja nicht vor. Ich glaube aber es gibt Gründe, das erste Newtonsche Axiom nicht als Spezialfall des zweiten zu betrachten. Also würde ich in keiner Einführung auf dieses Axiom verzichten, egal welchen Zugang man letztlich wählt. Und die kovariante Formulierung funktioniert wohl auch, wenn man nicht auf Basis des Äquivalenzprinzips die Bahnen frei fallender Testteilchen zu Geodäten macht.
| Zitat: |
Und warum sollte ich - und jeder Schüler - denn nicht kräftefrei mit frei fallend identifizieren? Das ist doch genau das, was ihm eine Waage als Kraftmesser sagt.
|
Wenn du kräftefrei mit frei fallend identifizierst ist entweder die Raumzeit gekrümmt oder das 1. Axiom ist verletzt. Denn frei fallende Teilchen bewegen sich in der flachen Raumzeit ja nicht geradlinig gleichförmig.
| Zitat: |
Je mehr ich darüber nachdenke, desto eher bin ich geneigt, einen alternativen Zugang zu suchen der die Newtonschen Axiome ersetzt. |
Hm, hast du da schon einen Vorschlag? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 10. Jun 2018 12:15 Titel: TomS Verfasst am: 10. Jun 2018 12:15 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Wenn du kräftefrei mit frei fallend identifizierst ist entweder die Raumzeit gekrümmt oder das 1. Axiom ist verletzt. Denn frei fallende Teilchen bewegen sich in der flachen Raumzeit ja nicht geradlinig gleichförmig. |
Genau. Das ist der Ausgangspunkt meiner Kritik.
| index_razor hat Folgendes geschrieben: |
| Zitat: |
Je mehr ich darüber nachdenke, desto eher bin ich geneigt, einen alternativen Zugang zu suchen der die Newtonschen Axiome ersetzt. |
Hm, hast du da schon einen Vorschlag? |
Wenn man die Newtonschen Begriffe beibehalten möchte, dann in der Konsequenz wohl nur um den Preis der gekrümmten Raumzeit.
Eine völlig andere Alternative wäre das Hamiltonsche Prinzip der minimalen Wirkung.
Gegenfrage: hast du einen Gegenvorschlag zu diesem intuitiven Kraftbegriff?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Systemdynamiker
Anmeldungsdatum: 22.10.2008
Beiträge: 594
Wohnort: Flurlingen
|
 Systemdynamiker Verfasst am: 11. Jun 2018 21:21 Titel: Impulserhaltung und Energieerhaltung Systemdynamiker Verfasst am: 11. Jun 2018 21:21 Titel: Impulserhaltung und Energieerhaltung |
 |
|
Meiner Meinung nach ist das erste Gesetz ein Spezialfall des zweiten. Zur Zeit Newtons war die Vorstellung einer kräftefreien, gleichförmigen Bewegung derart revolutionär, dass Newton dies - in Fortsetzung der Ideen von Galilei - durch ein separates Gesetz ausgedrückt hat.
Das zweite Problem ist die Definition der Kraft. Da gibt es untrschiedliche Ansichten. Die Unterscheidung zwischen einer Oberflächenkraft und der gravitativen Raumkraft ist für das Verständnis zentral. Eine Oberlächenkraft kann als Flächenintegral über den Spannungstensor definiert werden. Die Gravitationskraft ist gleich dem Volumenintegral über Dichte mal Gravitationsfeldsärke, wobei letztere auch Trägheitsfelder umfassen kann (Zentrifuge, linear beschleunigte Systeme).
_________________
Herzliche Grüsse Werner Maurer |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 13. Jun 2018 19:57 Titel: index_razor Verfasst am: 13. Jun 2018 19:57 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Wenn du kräftefrei mit frei fallend identifizierst ist entweder die Raumzeit gekrümmt oder das 1. Axiom ist verletzt. Denn frei fallende Teilchen bewegen sich in der flachen Raumzeit ja nicht geradlinig gleichförmig. |
Genau. Das ist der Ausgangspunkt meiner Kritik.
|
Du meinst, das ist ein Argument gegen das Trägheitsprinzip? Hm, ok, für mich ist die Frage an dieser Stelle eher, ob man das Trägheitsprinzip oder das Äquivalenzprinzip geometrisch interpretiert. (Oder eben beides innerhalb einer gekrümmten Raumzeit.) Ich habe ja weiter oben schon angedeutet, daß ich den Begriff der geradlinig-gleichförmigen Bewegung, den das Trägheitsprinzip verwendet, für grundlegend halte. Ich würde ein Prinzip, welches diese Bewegungsart einführt also verwenden.
Man kann dann immer noch sagen, daß ein frei fallender Körper eigentlich nicht kräftefrei ist, weil ja die Gravitationskraft auf ihn wirkt, aber davon nichts "spürt", weil die Gravitationskraft eben zufällig dem Äquivalenzprinzip genügt. Das ist aus rein theoretischer Sicht unschön, aber ohne vorher den ganzen differentialgeometrischen Ballast abzuladen wohl notwendig.
| Zitat: |
Eine völlig andere Alternative wäre das Hamiltonsche Prinzip der minimalen Wirkung. |
Ist denke ich auch machbar. Landau-Lifschitz führen ja die Dynamik ohne großes Brimborium über das Hamiltonsche Prinzip ein, und geben dafür eine sorgfältige Begründung für die Form der Lagrangefunktion eines freien Teilchens auf Basis von Symmetrieprinzipien. Das ist sehr elegant, aber als besonders einfach gelten die Bücher ja auch nicht gerade.
| Zitat: |
Gegenfrage: hast du einen Gegenvorschlag zu diesem intuitiven Kraftbegriff? |
Nein, eigentlich nicht. Ich glaube man muß den Kraftbegriff nicht schon innerhalb der ersten beiden Axiome sehr weit präzisieren. Ich fand eigentlich die Darstellung in Heil, Kitzka, Grundkurs theoretische Mechanik eine der einleuchtendsten Einführungen in die Mechanik auf Basis der Newtonschen Physik. Die ist zwar nicht kovariant, aber sehr sorgfältig bei der Diskussion der Grundlagen und Axiome. Nach den beiden bekannten Axiomen kommt noch ein Haufen weiterer, die den Kraftbegriff präzisieren. Dabei geht es hauptsächlich darum, wie mehrere Teilchen miteinander wechselwirken und welche Einschränkungen aus dem Relativitätsprinzip, Homogenität und Isotropie etc. folgen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 13. Jun 2018 20:47 Titel: TomS Verfasst am: 13. Jun 2018 20:47 Titel: |
 |
|
Meine Kritik richtig sich nicht gegen das Trägheitsgesetz, sondern gegen die naive und unpräzise Formulierung der Newtonschen Axiome und des Kraftbegriffes.
Wie ich oben ausgeführt habe - und du stimmst mir da ja zu - führt ein naiver, auf der Messung beruhende Kraftbegriff zwingend darauf, dass kräftefrei fallende Körper im Gravitationsfeld in einer flachen Raumzeit gerade nicht geradlinig gleichförmig bewegt sind.
Als Konsequenz darf dann entweder diese Körper nicht als kräftefrei bezeichnen, d.h. ich muss mich von dem auf einer naiven Messung beruhenden Kraftbegriff verabschieden, oder ich darf die Körper weiterhin als kräftefrei bezeichnen, muss jedoch eine nicht-triviale Geometrie einführen.
Letzteres kritisiere ich keineswegs; ich kritisieren die Naivität, die hinter der Einführung der Newtonschen Axiome steckt - nachdem wir heute wissen, wie die eigtl. geometrisch sinnvolle Vorgehensweise aussieht.
Das ist ein bisschen so wie in der Atomphysik: das Bohrsche Modell ist falsch und obsolet, trotzdem müssen die Schüler das lernen, nur um später zu erfahren, dass es falsch ist. Man zeichnet einen historischen Irrweg kritiklos und undidaktisch nach, anstatt ihn zu revidieren.
Ähnlich ist es hier auch. Stattdessen wäre die Suche nach Alternativen zu befürworten.
Evtl. lässt sich auf Basis des Hamiltonschen Prinzips eine einfache und dennoch widerspruchsfreie Formulierung finden. Der Kraftbegriff wäre nicht fundamental, aber sei’s drum. Eine gekrümmte Geometrie kann vermieden werden. Das lohnt schon eine weitere Diskussion.
Mich würde die Diskussion mit Schülern interessieren - ich teste das mal bei meiner Tochter (von Studenten erwarte ich, dass sie dem folgen können).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 13. Jun 2018 21:02 Titel: index_razor Verfasst am: 13. Jun 2018 21:02 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Meine Kritik richtig sich nicht gegen das Trägheitsgesetz, sondern gegen die naive und unpräzise Formulierung der Newtonschen Axiome und des Kraftbegriffes.
Wie ich oben ausgeführt habe - und du stimmst mir da ja zu - führt ein naiver, auf der Messung beruhende Kraftbegriff zwingend darauf, dass kräftefrei fallende Körper im Gravitationsfeld in einer flachen Raumzeit gerade nicht geradlinig gleichförmig bewegt sind.
|
Absolut. Ich glaube wir sind uns hier vollkommen einig. Die Frage scheint jetzt also zu lauten, wie sich das Äquivalenzprinzip in die Mechanik basierend auf dem Hamilton-Prinzip einfügt. Im Augenblick ist mir nicht klar, inwiefern da eine gekrümmte Raumzeit vermieden werden kann. Man muß doch trotzdem die stationären Bahnen irgendwie geometrisch interpretieren.
| Zitat: |
Mich würde die Diskussion mit Schülern interessieren - ich teste das mal bei meiner Tochter (von Studenten erwarte ich, dass sie dem folgen können). |
Würde mich auch interessieren. Bitte berichte gelegentlich von deinen Erfahrungen. |
|
 |
Systemdynamiker
Anmeldungsdatum: 22.10.2008
Beiträge: 594
Wohnort: Flurlingen
|
 Systemdynamiker Verfasst am: 13. Jun 2018 22:06 Titel: Impulsbilanz Systemdynamiker Verfasst am: 13. Jun 2018 22:06 Titel: Impulsbilanz |
 |
|
Meine Frage war, ob das erste Gesetz von Newton ein Spezialfall des zweiten ist. Die Diskussion ist dann ziemlich rasch in Richtung AR abgedriftet. Da sehe ich das erste Problem. Soll man heute im Unterricht (nicht nur an Schulen, sondern auch in Vorlesungen für Nichtphysiker) so tun, als ab Einstein nie gelebt hat?
Wie definiert man eine Kraft? Das war dann die Folgefrage. Zuerst muss man sich bewusst sein, dass im 2. Gesetz von Newton die resultierende Kraft und im 3. die Einzelkräfte gemeint sind. Für Newton war eine Kraft eine simple Wechselwirkung zwischen zwei Körpern. Das einzige für Newton quantitative beschreibbare Beispiel, die Gravitationskraft, hat sich mittlerweile in Geometrie aufgelöst. Die zwei weiteren Wechselwirkungen, die elektrische und die magnetische, die damals schon bekannt gewesen sind, haben mehrere Metamorphosen durchgemacht. Heute kann man zwei Antworten geben: die Lorentzkraft als Einwirkung des elektromagnetischen Feldes auf einen Körper oder die Viererdivergenz über den elektromagnetischen Energie-Impuls-Tensor als lokaler Austausch von Energie und Impuls zwischen Feld und geladener Materie (eine ähnliche Formulierung gibt es für die Gravitation, die schon Einstein angegeben hat).
Komplizierter wird die Sache, wenn man Kräfte und konvektive Impulsströme kombiniert, wie das bei einem Strahltriebwerk der Fall ist. Wenn man da Physiker ranlässt, wird es oft nur peinlich https://www.tagesanzeiger.ch/schweiz/standard/steuergelder-fuer-heisse-luft/story/19821920#mostPopularComment
_________________
Herzliche Grüsse Werner Maurer |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 13. Jun 2018 23:41 Titel: Re: Impulsbilanz TomS Verfasst am: 13. Jun 2018 23:41 Titel: Re: Impulsbilanz |
 |
|
| Systemdynamiker hat Folgendes geschrieben: | | Meine Frage war, ob das erste Gesetz von Newton ein Spezialfall des zweiten ist. |
Zunächst mal haben wir diskutiert, wie der Kraftbegriff hier definiert sein soll, bzw. dass er eben nicht definiert ist, was die von mir mehrfach genannte Inkonsistenz zur Folge hat.
| Systemdynamiker hat Folgendes geschrieben: | | Die Diskussion ist dann ziemlich rasch in Richtung AR abgedriftet. |
Das war nicht die Absicht, ist jedoch eine mögliche Konsequenz, wenn eine sinnvolle Definition des Kraftbegriffs sucht und Newton (1 - 3) konsistent interpretieren möchte.
| Systemdynamiker hat Folgendes geschrieben: | | Wie definiert man eine Kraft? Das war dann die Folgefrage. |
Zunächst mal versuchsweise über einen Kraftmesser wie z.B. eine Federwaage.
Dabei stellt sich die Frage, in welchem System deren Aufhängung fixiert sein soll. Es bietet sich an, dafür ein System zu benutzen, in dem der Aufhängepunkt selbst frei fallend ist, d.h. in dem ein mitbewegter Beobachter keine Kraft spürt. Dasvführtnzwanglos zum Begriff des Inertialsystems, allerdings entsprechend ART. Der Vorteil ist, dass der Kraftbegriff messtechnisch eingeführt wird und dass man „geradlinig gleichförmig“ nicht explizit nutzen muss.
Allerdings führt dies eben gerade nicht auf die Newtonsche Mechanik.
| Systemdynamiker hat Folgendes geschrieben: | | Zuerst muss man sich bewusst sein, dass im 2. Gesetz von Newton die resultierende Kraft und im 3. die Einzelkräfte gemeint sind. |
Was wiederum darauf hin deutet, dass der Kraftbegriff dringend präzisiert werden muss.
| Systemdynamiker hat Folgendes geschrieben: | | Das einzige für Newton quantitative beschreibbare Beispiel, die Gravitationskraft, hat sich mittlerweile in Geometrie aufgelöst. |
Ein sehr einfaches Beispiel wäre die Federkraft.
Der Unterschied zur Gravitationskraft ist evident: Wenn ausschließlich die Gravitationskraft auf einen ansonsten freien Körper wirkt, spürt dieser keine resultierende Kraft sondern“fällt frei“. Wenn ausschließlich eine Federkraft auf einen ansonsten freien Körper wirkt und dieser beschleunigt wird, spürt ein mitbewegter Beobachter die Trägheitskraft.
Zur Diskussion deiner Frage | Systemdynamiker hat Folgendes geschrieben: | | ..., ob das erste Gesetz von Newton ein Spezialfall des zweiten ist |
fehlt mir immer noch eine Definition der verwendeten Begriffe und die Auflösung der o.g. Widersprüche.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 13. Jun 2018 23:48 Titel: TomS Verfasst am: 13. Jun 2018 23:48 Titel: |
 |
|
Aus der engl. Wikipedia.
https://en.m.wikipedia.org/wiki/Newton%27s_laws_of_motion
https://en.m.wikipedia.org/wiki/Inertial_reference_frame
| Zitat: | First law: In an inertial frame of reference, an object either remains at rest or continues to move at a constant velocity, unless acted upon by a force.[2][3]
Second law: In an inertial reference frame, the vector sum of the forces F on an object is equal to the mass m of that object multiplied by the acceleration a of the object: F = ma. (It is assumed here that the mass m is constant – see below.)
An inertial frame of reference in classical physics and special relativity is a frame of reference in which a body with zero net force acting upon it is not accelerating.
Newton's laws hold only with respect to a certain set of frames of reference called Newtonian or inertial reference frames. Some authors interpret the first law as defining what an inertial reference frame is; from this point of view, the second law holds only when the observation is made from an inertial reference frame, and therefore the first law cannot be proved as a special case of the second. Other authors do treat the first law as a corollary of the second.[11][12]. |
In dieser Form ist das natürlich zirkulär.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 14. Jun 2018 00:08 Titel: VeryApe Verfasst am: 14. Jun 2018 00:08 Titel: |
 |
|
@ tomS könntest du mir folgendes erklären.
https://www.youtube.com/watch?v=LxRvEfyFJu8
da ist ein Frosch im Magnetfeld. Er besteht zu größten Teil aus Wasser (Diamagnetismus).
wenn der Frosch sich nicht dauernd mit seinen Füssen am Zylinder abstossen würde, würde er ruhig schweben.
Der Frosch spürt auch nichts, dann müsste ja dann nach deiner Angabe Frosch spürt nichts keine Kraft wirken oder?=
Aus der Tatsache das man nichts spürt kann man nicht schließlich das nichts wirkt 
Wenn alle einzelteile durch Kräfte ungefähr gleich beschleunigt werden, spürt man eben nichts.
Wenn auf ein objekt nur die Gravitationskraft wirkt, braucht man nur durchschneiden und sieht sofort wieso man nichts spürt, weil keine Kräfte im Schnitt übertragen werden müssen. weil sie in jeden Massepunkt gleich ansetzt
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 14. Jun 2018 00:19 Titel: TomS Verfasst am: 14. Jun 2018 00:19 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | | Der Frosch spürt auch nichts, dann müsste ja dann nach deiner Angabe Frosch keine Kraft wirken oder? |
Ja, die Summe aller Kräfte ist Null, der Frosch bewegt sich kräftefrei.
| VeryApe hat Folgendes geschrieben: | | Aus der Tatsache das man nichts spürt kann man nicht schließlich das nichts wirkt |
Habe ich so auch nicht behauptet.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 14. Jun 2018 00:25 Titel: VeryApe Verfasst am: 14. Jun 2018 00:25 Titel: |
 |
|
| Zitat: |
Ja, die Summe aller Kräfte ist Null, der Frosch bewegt sich kräftefrei.
|
hast du nicht vorher geschrieben am besten wäre ein freifallendes Bezugssystem als Inertialsystem.
indem würde aber der Frosch nach oben beschleunigen und das Kräfte frei?
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 14. Jun 2018 02:13 Titel: TomS Verfasst am: 14. Jun 2018 02:13 Titel: |
 |
|
Es geht mir um die Definition des Kraftbegriffes.
Gemäß Newton I bewegt sich ein kräftefreier Körper in einem Inertialsystem geradlinig gleichförmig. Man könnte also das bzgl. der Erdoberfläche ortsfeste Bezugsystem als Inertialsystem bezeichnen. In diesem ist der Frosch kräftefrei, und er bewegt sich geradlinig gleichförmig. Die Beschleunigung und die Gesamtkraft sind Null. Passt also.
Nur: für andere Körper gilt dies nicht. Ein frei fallender Beobachter ohne elektromagnetische Kraft ist ebenfalls kräftefrei. Man könnte also dessen Ruhesystem als Inertialsystem verwenden. In diesem ist der frei fallende Beobachter kräftefrei, und er bewegt sich geradlinig gleichförmig. Die Kraft, die der frei fallende Beobachte spürt, ist Null. Passt also ebenfalls.
Beide Ansätze sind in sich konsistent, jedoch sind die Ansätze untereinander nicht verträglich.
Bzgl. des frei im Gravitationsfeld der Erde fallenden Beobachters ist der Frosch nicht kräftefrei, bzgl. des Frosches ist der frei fallende Beobachter nicht kräftefrei.
Ich wollte zunächst nicht darauf hinaus, das das eine besser ist als das andere, sondern darauf, dass der Begriff Inertialsystem noch nicht eingeführt und der Begriff Kraft noch nicht eindeutig definiert ist.
Betrachten wir zuletzt den Fall eines massebehafteten und elektrisch geladenen Körpers, einmal im Gravitationsfeld, einmal im Coulombfeld. In beiden Fällen liegt ein 1/r Potential vor, dennoch sind beide Fälle fundamental verschieden. Der elektrisch geladene Körper wird im Coulombfeld beschleunigt und spürt eine Trägheitskraft. Der massebehafteten Körper wird im Gravitationsfeld beschleunigt, spürt jedoch keine Trägheitskraft. Für den massebehafteten Körper im Gravitationsfeld fühlt sich die Situation kräftefrei an, für den elektrisch geladene Körper im Coulombfeld dagegen nicht.
Dies alles ist in den Newtonschen Axiomen nicht geklärt. Definition von Kraft und Inertialsystem erscheinen irgendwie zirkulär. Im Falle von Einstein ist dagegen alles wunderbar logisch.
Man hat offensichtlich mehrere Möglichkeiten:
1) man bleibt trotz diverser Unzulänglichkeiten bei den Newtonschen Axiomen und ignoriert die o.g. Probleme
2) man folgt Einstein bei der Definition von Inertialsystemen und landet bei der ART
3) man verzichtet auf die Kraft als fundamentale Größe und leitet die klassische Mechanik aus dem Hamiltonschen Prinzip ab
Ich halte den Versuch, das Trägheitsprinzip im Kontext von (1) besser verstehen zu wollen, für Zeitverschwendung. Wenn man am Trägheitsprinzip interessiert ist, ist (2) der richtige Ansatz. Wenn das Ziel die widerspruchsfreie Formulierung der klassischen Mechanik ist, dann ist (3) das Mittel der Wahl. (2) und (3) sind übrigens miteinander verträglich.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 14. Jun 2018 08:32 Titel: VeryApe Verfasst am: 14. Jun 2018 08:32 Titel: |
 |
|
| Zitat: | Es geht mir um die Definition des Kraftbegriffes.
Gemäß Newton I bewegt sich ein kräftefreier Körper in einem Inertialsystem geradlinig gleichförmig. Man könnte also das bzgl. der Erdoberfläche ortsfeste Bezugsystem als Inertialsystem bezeichnen. In diesem ist der Frosch kräftefrei, und er bewegt sich geradlinig gleichförmig. Die Beschleunigung und die Gesamtkraft sind Null. Passt also.
Nur: für andere Körper gilt dies nicht. Ein frei fallender Beobachter ohne elektromagnetische Kraft ist ebenfalls kräftefrei. Man könnte also dessen Ruhesystem als Inertialsystem verwenden. In diesem ist der frei fallende Beobachter kräftefrei, und er bewegt sich geradlinig gleichförmig. Die Kraft, die der frei fallende Beobachte spürt, ist Null. Passt also ebenfalls.
Beide Ansätze sind in sich konsistent, jedoch sind die Ansätze untereinander nicht verträglich.
Bzgl. des frei im Gravitationsfeld der Erde fallenden Beobachters ist der Frosch nicht kräftefrei, bzgl. des Frosches ist der frei fallende Beobachter nicht kräftefrei.
Ich wollte zunächst nicht darauf hinaus, das das eine besser ist als das andere, sondern darauf, dass der Begriff Inertialsystem noch nicht eingeführt und der Begriff Kraft noch nicht eindeutig definiert ist.
|
1 Axiom Körper bewegt sich geradlinig gleichförmig ohne Kräfte
2 Axiom jede einzelne Kraft bewirkt eine beschleunigung - > darauf folgt ide resultierende Kraft bewirkt die resultierende Beschleunigung
3 Axiom für jede einzelne Kraft von A->B gibt es eine entgegengesetze Kraft von B->A
würdest du hergehen und ein freifallendes Bezugssystem als Inertialsystem taufen, dann würden da aus heiterem himmel die gesamte Erde und alle Dinge drauf nach oben beschleunigen.
Nach dem 1 Axiom erfordert das eine Kraft.
und nach dem 3Axiom ist das kein Inertialsystem weil es das wechselwirkungsgesetz nicht erfüllt und die Erde da ohne Wechselwirkung aus heiterem himmel nach oben Beschleunigt.
im Inertialsystem nach Newton müssen alle drei Gesetze erfüllt sein.
Dann hast du ja geschrieben müsste man die Krümmung des Raumes erklären.
Wenn nicht hat man die Gravitationskraft.
Problem ist dann nicht spürbar ?
Wenn Kräfte so wirken das sie jeden Massepunkt gleich beschleunigen sind sie nicht spürbar. Das Problem hätte man doch immer. egal was du da als Inertialsystem definierst.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 14. Jun 2018 09:06 Titel: TomS Verfasst am: 14. Jun 2018 09:06 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | 1 Axiom Körper bewegt sich geradlinig gleichförmig ohne Kräfte
würdest du hergehen und ein freifallendes Bezugssystem als Inertialsystem taufen, dann würden da aus heiterem himmel die gesamte Erde und alle Dinge drauf nach oben beschleunigen. |
Nochmal: das Problem mit Newton 1 ist, dass der Kraftbegriff nicht definiert ist!
Also definieren wir ihn: wir definieren die Kraft bzgl. eines mit einem Körper mitbewegten Bezugsystems; wenn der Körper keine Kraft spürt und bzgl. dieses Bezugsystems keine Kraft messbar ist, dann sei der Körper kräftefrei.
Das funktioniert für diverse Kräfte: keine Federkraft - OK, keine elektrische Kraft - OK, keine Reibungskraft - OK.
| VeryApe hat Folgendes geschrieben: | | Wenn Kräfte so wirken das sie jeden Massepunkt gleich beschleunigen sind sie nicht spürbar. Das Problem hätte man doch immer. egal was du da als Inertialsystem definierst. |
Offensichtlich nicht. Jede der o.g. Kräfte ist spürbar, außer der Gravitationskraft. Wenn ein Körper durch Reibung abgebremst wird, spürt man die Trägheitskraft. Wenn ein Körper durch einen Raketenantrieb beschleunigt wird, spürt man die Trägheitskraft. Wenn ein Körper im Coulombfeld beschleunigt wird, spürt man die Trägheitskraft. Wenn ein Körper im Gravitationsfeld beschleunigt wird, spürt man keine Trägheitskraft.
Nur für die Gewichtskraft funktioniert das also nach Newton nicht. Man kann das Inertialsystemen als frei fallendes Bezugsystem definieren, und damit funktioniert bei Newton alles wie gewohnt, außer der Betrachtung von Gravitationskräften.
Das Problem der Newtonschen Axiome in dieser Form ist, dass „Kraft“ bzw. „kräftefrei“ und „Inertialsystem“ zirkulär eingeführt bzw. nicht präzise definiert werden. Die Axiome verwenden den Begriff „Kraft“ ohne ihn zu definieren. Der Versuch einer anschaulichen Erklärung mittels der gemessenen Kraft führt auf das o.g. Problem für die Gravitation.
| VeryApe hat Folgendes geschrieben: | | würdest du hergehen und ein freifallendes Bezugssystem als Inertialsystem taufen, dann würden da aus heiterem himmel die gesamte Erde und alle Dinge drauf nach oben beschleunigen. |
Es geht darum, den Begriff nicht-zirkulär zu definieren. Mein Ansatz führt auf die Definition des Inertialsystems nach Einstein. Wir sind uns hoffentlich einig, dass das in sich konsistent ist: ein frei fallender = kräftefreier Körper definiert lokal ein Inertialsystem, er bewegt sich geradlinig und gleichförmig, jedoch bzgl. einer verallgemeinerten Geometrie. Die Gravitation ist in diesem Sinne keine Kraft.
Der Versuch, dies gemäß Newton durchzuführen, führt auf ein offensichtliches und ganz anschauliches Problem, das du noch nicht erklären konntest:
Axiom 1: „ein Körper bewegt sich geradlinig gleichförmig ohne Kräfte“
Beobachtung: „ein frei fallender Körper im Gravitationsfeld ist messbar kräftefrei“
weitere Beobachtung: „ein frei fallender Körper im Gravitationsfeld bewegt sich entlang einer Ellipse oder einer Hyperbel“
Schlussfolgerung: es existiert ein Widerspruch zu Axiom 1.
Wie löst du dieses Problem nach Newton? Wie definierst du also „Inertialsystem“, „geradlinig gleichförmig“ sowie „Kraft“ und „kräftefrei“ - nicht-zirkulär - so dass diese Probleme vermieden werden?
EDIT: ich verlange nicht, dass du meiner Schlussfolgerung in Richtung Einstein folgst; ich denke, du kannst zustimmen, dass sie eine mögliche Lösung darstellt. Außerdem solltest du zustimmen, dass die Newtonschen Axiome ohne weitere Erklärung unvollständig bzw. teilweise zirkulär erscheinen und zu dem o.g. Problem führen. Du kannst dann gerne eine andere Präzisierung vorschlagen, die am Newtonschen Paradigma festhält.
Aus der Diskussion folgt m.E., dass man Newton 1 als unabhängig betrachten sollte, da es auch in der ART gültig bleibt und zur Definition von Inertialsystemen herangezogen werden kann. Newton 2 kann dann durch die Geodätengleichung plus Terme mit „echten“ Kräften ersetzt werden.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 14. Jun 2018 09:47 Titel: VeryApe Verfasst am: 14. Jun 2018 09:47 Titel: |
 |
|
| Zitat: | | Das funktioniert für diverse Kräfte: keine Federkraft - OK, keine elektrische Kraft - OK, keine Reibungskraft - OK. |
| Zitat: | | Offensichtlich nicht. Jede der o.g. Kräfte ist spürbar, außer der Gravitationskraft |
Und wo ist jetzt der Frosch obwohl auf ihn eine Kraft wirkt spürt er nichts.
würde ich lauter minifeder am Körper anbringen können und das in seinen einzelnen Masseteilen würde er auch nichts spüren und keine Belastung vorweisen.
würde ich einen geladenen Körper haben der aus den gleichen Material besteht würde er auch nichts spüren und keine Belastung aufweisen.
| Zitat: |
Wie löst du dieses Problem nach Newton? Wie definierst du also „Inertialsystem“, „geradlinig gleichförmig“ sowie „Kraft“ und „kräftefrei“ - nicht-zirkulär - so dass diese Probleme vermieden werden? |
Leider kann ich das m.E. nicht lösen, weil man aus der Tatsache das man lokal nichts messen kann nicht schließen kann das nichts wirkt.. Man muß postulieren das etwas wirkt oder nicht wirkt und schauen ob es aufgeht,
wie macht einstein das den beim Frosch.
Offensichtlich ist der kräftefrei denn er spürt auch nichts . trotzdem beschleunigt er auf das freifallende Bezugssystem-
Krümmt jetzt das Magnetfeld den Raum so lokal das er ruhen kann, oder wie funktioniert das jetzt?
ich schlage hier gar nichts vor, ich stelle nur Fragen.-
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 14. Jun 2018 12:06 Titel: TomS Verfasst am: 14. Jun 2018 12:06 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: | | Und wo ist jetzt der Frosch obwohl auf ihn eine Kraft wirkt spürt er nichts. |
Im Falle des Frosches liegt ja eine Summe von realen Kräften vor, die sich zu Null addieren. Das ist etwas anderes, als dass jede einzelne Kraft verschwindet.
| VeryApe hat Folgendes geschrieben: | | Leider kann ich das m.E. nicht lösen, weil man aus der Tatsache das man lokal nichts messen kann nicht schließen kann das nichts wirkt. |
Das ist nicht der Punkt. Es geht zunächst mal um eine Definition.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 14. Jun 2018 14:26 Titel: index_razor Verfasst am: 14. Jun 2018 14:26 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: |
wie macht einstein das den beim Frosch.
Offensichtlich ist der kräftefrei denn er spürt auch nichts . trotzdem beschleunigt er auf das freifallende Bezugssystem-
|
Nein, laut Einstein ist der Frosch nicht kräftefrei, wenn er nicht frei fällt. Stell es dir so vor: die Bewegungsgleichung des Frosches ist sowas in der Art
^i}{m}.)
(natürlich noch summiert über alle Dipole etc.) Links steht die Beschleunigung, rechts die Kraft pro Masse. Daß der Frosch schwebt oder ruht, bedeutet nun lediglich 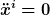 , aber nicht, daß er unbeschleunigt ist. Du bist zwar gewohnt, den Term , aber nicht, daß er unbeschleunigt ist. Du bist zwar gewohnt, den Term

als (negative) Kraft pro Masse anzusehen und nicht als Beschleunigung, aber Einstein lädt dich ein, in diesem Punkt umzudenken. Und aus Newtons Sicht besteht kein theoretisch zwingender Einwand. Im Gegenteil: es besteht genau dieselbe theoretische Motivation dafür, nämlich das Äquivalenzprinzip. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 14. Jun 2018 19:06 Titel: DrStupid Verfasst am: 14. Jun 2018 19:06 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Nochmal: das Problem mit Newton 1 ist, dass der Kraftbegriff nicht definiert ist! |
Newton 1 ist Teil der Definition. Der Newtonsche Kraftbegriff wird durch die Newtonschen Axime definiert.
| TomS hat Folgendes geschrieben: | | Also definieren wir ihn: [...] |
Das ist die Quelle der von Dir behauteten Inkonsistenzen. Wenn Du einfach irgendwelche Privatdefinitionen für die Kraft erfindest, dann darfst Du Dich nicht wundern, wenn am Ende nichts mehr zusammen passt. |
|
 |
|
|
















