| Autor |
Nachricht |
Gast1001
Anmeldungsdatum: 10.03.2024
Beiträge: 2
|
 Gast1001 Verfasst am: 10. März 2024 20:20 Titel: QM harmonischer Oszillator Gast1001 Verfasst am: 10. März 2024 20:20 Titel: QM harmonischer Oszillator |
 |
|
Meine Frage:
Bin noch ganz am Anfang und verstehe einige grundlegende Sachen zur Energie des Oszillators nicht. Die diskreten Energieniveaus sind ja durch
 )
gegeben. Sind dies die kinetischen Energien oder die Gesamtenergien? Außerdem habe ich bei Wikipedia folgendes gefunden: "Bei jedem physikalischen System erfüllen Energie E und Kreisfrequenz  seiner quantenmechanischen Phase die Gleichung seiner quantenmechanischen Phase die Gleichung  ". Ist in dieser Formel E nur die kinetische Energie oder die Gesamtenergie und ist das ". Ist in dieser Formel E nur die kinetische Energie oder die Gesamtenergie und ist das  in den beiden Gleichungen dasselbe, oder ist das nur zufällig dieselbe Bezeichung. Dankeschön in den beiden Gleichungen dasselbe, oder ist das nur zufällig dieselbe Bezeichung. Dankeschön
Meine Ideen:
Also die erste Formel erhält man ja durch Lösen der stationären SGL, da hat man gar keinen Zeitanteil. Ich würde vermuten in der ersten Formel beschreibt das  wie gestreckt/gestaucht das Parabelpotential ist und in der zweiten Formel mit welcher Kreisfrequenz die Wellenfunktion zeitlich schwinkt, wenn man den Zeitanteil mitdran multipliziert. Deswegen glaube ich, dass das wie gestreckt/gestaucht das Parabelpotential ist und in der zweiten Formel mit welcher Kreisfrequenz die Wellenfunktion zeitlich schwinkt, wenn man den Zeitanteil mitdran multipliziert. Deswegen glaube ich, dass das  in beiden Gleichungen unterschiedlich ist und nur zufällig gleich bezeichnet ist. in beiden Gleichungen unterschiedlich ist und nur zufällig gleich bezeichnet ist. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18086
|
 TomS Verfasst am: 10. März 2024 21:18 Titel: Re: QM harmonischer Oszillator TomS Verfasst am: 10. März 2024 21:18 Titel: Re: QM harmonischer Oszillator |
 |
|
| Gast1001 hat Folgendes geschrieben: | Die diskreten Energieniveaus sind ja durch
 )
gegeben. Sind dies die kinetischen Energien oder die Gesamtenergien? |
Es sind die Eigenwerte des Gesamt-Hamiltonoperators, also die Gesamtenergien.
Die kinetischen Energien sind – wie im klassischen Fall – nicht konstant.
| Gast1001 hat Folgendes geschrieben: | Außerdem habe ich bei Wikipedia folgendes gefunden: "Bei jedem physikalischen System erfüllen Energie E und Kreisfrequenz  seiner quantenmechanischen Phase die Gleichung seiner quantenmechanischen Phase die Gleichung  ". Ist in dieser Formel E nur die kinetische Energie oder die Gesamtenergie und ist das ". Ist in dieser Formel E nur die kinetische Energie oder die Gesamtenergie und ist das  in den beiden Gleichungen dasselbe, oder ist das nur zufällig dieselbe Bezeichung. in den beiden Gleichungen dasselbe, oder ist das nur zufällig dieselbe Bezeichung. |
Es ist in dieser allgemeinen Form nicht mal richtig. "Bei jedem abgeschlossenen System …" ist zutreffend.
Es handelt sich wieder um die Gesamtenergie eines stationären Zustandes.
| Gast1001 hat Folgendes geschrieben: | Ich würde vermuten in der ersten Formel beschreibt das  wie gestreckt/gestaucht das Parabelpotential ist … wie gestreckt/gestaucht das Parabelpotential ist … |
Richtig. Das ist völlig analog zur klassischen Gleichung. Siehe jedoch das folgende.
| Gast1001 hat Folgendes geschrieben: | … und in der zweiten Formel mit welcher Kreisfrequenz die Wellenfunktion zeitlich schwinkt, wenn man den Zeitanteil mitdran multipliziert. Deswegen glaube ich, dass das  in beiden Gleichungen unterschiedlich ist und nur zufällig gleich bezeichnet ist. in beiden Gleichungen unterschiedlich ist und nur zufällig gleich bezeichnet ist. |
Nein, es ist das selbe.
Bei der stationären Schrödingergleichung hat man lediglich die zeitabhängige e-Funktion bereits gekürzt.
Das omega ist erst ein Ergebnis der Lösung der Schrödingergleichung. Dabei erkennt man, dass es aus der Form des Potentials folgt, und schreibt deswegen das Potential gerne unter Verwendung von omega. Ursprünglich steckt es da jedoch noch nicht drin.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Gast1001
Anmeldungsdatum: 10.03.2024
Beiträge: 2
|
 Gast1001 Verfasst am: 11. März 2024 18:44 Titel: Gast1001 Verfasst am: 11. März 2024 18:44 Titel: |
 |
|
Das hilft mir schonmal weiter. Vielen Dank. Ich glaube, dass ich die Gleichung  im Kontext der QM noch nicht richtig verstehe. Die beiden obigen Gleichungen sind ja unterschiedlich. Welche beschreibt den jetzt genau die Gesamtenergie richtig? Für im Kontext der QM noch nicht richtig verstehe. Die beiden obigen Gleichungen sind ja unterschiedlich. Welche beschreibt den jetzt genau die Gesamtenergie richtig? Für  liefert die erste Gleichung ja höhere Energien. liefert die erste Gleichung ja höhere Energien.
Also ich kam auf die Frage, da im Lehrbuch bei der SGL für den Oszillator:

die Ersetzungen

und

gemacht werden und ich nicht ganz verstehe warum man bei C nicht 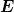 und und  gegeneinander wegkürzen darf. Dann noch eine Frage, wenn ich die Lösung für die stationäre SGL habe, kann ich für die vollständige Lösung einfach den Term gegeneinander wegkürzen darf. Dann noch eine Frage, wenn ich die Lösung für die stationäre SGL habe, kann ich für die vollständige Lösung einfach den Term  dran multiplizieren und dann für dran multiplizieren und dann für  wiederum wiederum
\hbar\omega )
einsetzten oder? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18086
|
 TomS Verfasst am: 12. März 2024 08:04 Titel: TomS Verfasst am: 12. März 2024 08:04 Titel: |
 |
|
Sorry, ich hatte deine Frage falsch verstanden; meine Antwort hat wohl mehr verwirrt als geholfen; wie auch immer.
1. Aus der de-Broglischen Theorie der Materiewellen für nicht-relativistische freie Teilchen mit

kennt man die Zusammenhänge
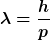

Dabei verwendet man häufig


und damit
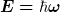
2. Die zeitabhängige Schrödingergleichung ist in gewisser Weise eine Verallgemeinerung dieser Theorie unter Berücksichtigung von Wechselwirkungen, d.h. auch Potentialen. Für die Lösung verwendet man häufig den Separationansatz
 = e^{-i\omega t} \, u(x))
wobei die ortsabhängigen Funktionen u(x) dann den Eigenfunktionen des Hamiltonoperators H zum Energie-Eigenwert E entsprechen:
 \, u_E(x) = 0)
Dabei gilt wiederum wie bei de Broglie
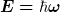
3. Beim harmonischen Oszillator tritt dessen Winkelfrequenz Omega anders auf.
Man betrachtet das klassische Potential
 = \frac{1}{2}k x^2)
und die klassische Schwingungsfrequenz Omega gemäß

Damit haben wir
)
 = e^{-i\omega_nt} u_n(x))
Die Verwirrung tritt also letztlich dann auf, wenn man das Potential des harmonischen Oszillators durch die klassische Frequenz Omega ausdrückt, und wenn man dabei nicht von der Frequenz der Lösung der zeitabhängigen Schrödingergleichung unterscheidet.
Man erhält quantenmechanische Zustände mit dieser klassischen Schwingungsfrequenz Omega mittels der Konstruktion sogenannter kohärenter Zustände. Dabei handelt es sich jedoch nicht um Energie-Eigenzustände, die eben immer diese n-abhängige Frequenz omega aufweisen.
Das sind jedoch alles spezifische Fragen für den harmonischen Oszillator.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|















