| Autor |
Nachricht |
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
 MCF Verfasst am: 05. Dez 2006 19:54 Titel: gedämpfter Oszillator |
 |
|
hallooo 
gegeben ist die bewegungsgleichung
die frage ist, für welchen wert omega folgende funktion eine lösung ist:
 = x_0 \cdot e^{( (- \gamma/2) \cdot t)} \cdot \cos (\omega t))
also ich habe mir die 2. fkt mal zerlegt und weiß, dass cos (wt) ja die harmonische schwingung ist und e^( (- ɣ/2) t) aus dem negativen, sowie dem postitven gegen die xachse verläuft. also liegt meine funktion im grunde graphisch gesehn dazwischen..
die amplitude wird kleiner je länger es schwingt.
http://www.paraview.de/help/hilfe/beispielehtml/spielwiese/gedaempfte-schwingung.gif
ich kann mir auch vorstellen, dass ich die erste fkt erst mal 2x ableiten muss, damit ich mit meinem w variieren kann, ... so, jetzt ihr, wie mach ich das?? 
grüüüße
[TeX, para] |
|
 |
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 05. Dez 2006 20:19 Titel: |
|
|
Einverstanden, du rechnest dir das ) aus, indem du das ) einmal nach der Zeit ableitest, und das ) rechnest du dir aus, indem du das dann nochmal nach der Zeit ableitest.
Dann kannst du das , das und das in deine Differentialgleichung einsetzen und dann durch geschicktes Rechnen und Umformen herausfinden, für welchen Wert der Kreisfrequenz  diese Gleichung stimmt. |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 05. Dez 2006 20:39 Titel: |
|
|
|
wie lautet denn die produktregel bei 3 fakotren? |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 05. Dez 2006 20:40 Titel: |
|
|
|
Der erste Faktor ist konstant, da reicht dir hier also die Produktregel für 2 Faktoren. |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 05. Dez 2006 21:06 Titel: |
|
|
 )
ok? |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 05. Dez 2006 21:09 Titel: |
|
|
Du hast zwar ein paar Klammern vergessen, aber du meinst das richtige. OK  |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 05. Dez 2006 21:36 Titel: |
|
|
|
wo denn klammern vergessen?? |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 05. Dez 2006 21:41 Titel: |
|
|
Mit den nötigen Klammern sieht das ganze so aus:
 * e^{-\frac{\gamma}{2}* t} * cos (w * t) + e^{-\frac{\gamma}{2}* t} * w * (-sin (wt)) ) |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 05. Dez 2006 21:46 Titel: |
|
|
ahh klar.. *g
bei der x(t)'' brauch ich hilfe.. |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 05. Dez 2006 21:48 Titel: |
|
|
|
Tipp: Wenn du die erste Ableitung geschafft hast, dann schaffst du auch die zweite. Die zweite ist nämlich nicht schwieriger, sondern nur ein bisschen mehr Schreibarbeit. |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 05. Dez 2006 21:54 Titel: |
|
|
tipp befolgt^^
^2 * e^{- \frac{\gamma}{2}*t}*w*(-sin(wt))+(-\frac{\gamma}{2})* e^{- \frac{\gamma}{2}*t}*w^2(-cos(wt)) ) |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 05. Dez 2006 22:07 Titel: |
|
|
|
Wie hast du das gerechnet? Dein Ergebnis kann ich noch nicht so recht nachvollziehen. Ich hätte erwartet, dass du nun beim zweiten Mal Ableiten zunächst vier Terme bekommst. |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 05. Dez 2006 22:15 Titel: |
|
|
uiii.. also...
^2 * e^{- \frac{\gamma}{2}*t}*cos(wt)+ (-\frac{\gamma}{2})*e^{- \frac{\gamma}{2}*t}*w*(-sin(wt)) + \frac{\gamma}{2}* e^{- \frac{\gamma}{2}*t}*w*(-sin(wt))+e^{- \frac{\gamma}{2}*t}*w^2(-cos(wt))
<br />
)
better? |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 05. Dez 2006 22:39 Titel: |
|
|
Much better Nur im dritten Term hast du noch ein Minuszeichen vergessen.
Jetzt kannst du das ganze möglichst sauber und übersichtlich aufschreiben (am besten noch, soweit möglich, ein bisschen zusammenfassen), dann tief Luft holen und alles in die DGL einsetzen |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 05. Dez 2006 22:48 Titel: |
|
|
1. du meinst das - vor dem bruch??
2. wo kann ich denn da was zusammenfassen??
3. ich setze also in meine bewegungsgleichung für x'' die zweite, für x' die erste ableitung und für x anfangsgleichung ein?
4. ich habs grad einfach alles eingesetzt und fühl mich überfordert 
also.. ich weiß gar nicht richtig, wie ich damit umgehen soll.. ich habe mir jetzt ein paar einzelteile rausgepickt un zusammengeklatscht^^
7 *  + 3*  + ^2 ) + 3 * (w*(-sin(wt))) + 3*x0 + 2*cos(wt) + w^2 * (-cos(wt))+w0^2
Zuletzt bearbeitet von MCF am 05. Dez 2006 23:11, insgesamt einmal bearbeitet |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 05. Dez 2006 23:10 Titel: |
|
|
1. da steht ja "e hoch MINUS gamma/2", also musst du das Minus beim Ableiten mit dem gamma/2 davorziehen.
2. Schau dir zum Beispiel mal ganz scharf den zweiten und den dritten Term an (nachdem du den Vorzeichenfehler aus 1. korrigiert hast)
3. Ja.
4. Ich glaube, da hilft nur:
* Vorher sehr gut schauen, was du zusammenfassen und ausklammern kannst, so dass das so übersichtlich wie möglich wird
* Ein Blatt Papier quer nehmen, sehr sauber schreiben und sehr sorgfältig rechnen
* Nicht nur mechanisch rechnen, sondern viel schauen, ob und wann du irgendetwas übersichtlicher schreiben, ausklammern oder herauskürzen kannst.
* Eine optimale Uhrzeit wählen, um dich dieser Herausforderung mit frischem Kopf zu stellen (Es gibt Leute, die so etwas abends um 23.00 Uhr nicht mehr hinbekommen, dafür haben sie zu anderen Uhrzeiten eine echte Chance ) |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 05. Dez 2006 23:18 Titel: |
|
|
|
also war mein ansatz totaler humbug? |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 05. Dez 2006 23:24 Titel: |
|
|
Überhaupt nicht!
Du bist bisher genau den richtigen Weg gegangen.
Den Vorzeichenfehler aus 1. musst du noch korrigieren, und dein Ansatz, das nun alles in die DGL einzusetzen, ist genau richtig (siehe "3. Ja").
Um diesen Weg nun sauber durchzuziehen, brauchst du nun wahrscheinlich einfach noch Tipps wie die aus 4., damit du durch diese Rechnung durchkommst, obwohl du mir den Eindruck zu haben scheinst, dass du bisher noch nicht so oft mit so "langen" Gleichungen gerechnet hast, und dass das für dich noch ein bisschen was von dem Gefühl einer "neuen Herausforderung" hat, da fehlerfrei durchzukommen. |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 05. Dez 2006 23:25 Titel: |
|
|
hast du den editierten beitrag auf seite 1 gesehn?
"herausforderung" triffts voll und ganz |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 06. Dez 2006 00:08 Titel: |
|
|
Jetzt habe ich das Edit gesehen. Ich kann allerdings nicht nachvollziehen, wie du auf diese Terme kommst.
Ich schlage vor, am besten machst du das Ganze schrittweise, eins nach dem anderen.
Was bekommst du für die zweite Ableitung des Ortes nach der Zeit, wenn du den Vorzeichenfehler, den ich in 1. angesprochen habe, korrigierst? |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 06. Dez 2006 00:14 Titel: |
|
|
wär toll, wenn wir das heut noch hinbekämen, würd mir sehr weiterhelfen den fehler habe ich korrigiert. aber ich weiß nicht, ob es sinnvoll ist, einen ganzen term rauszunehmen...
ich habe bei meinem edit quasi die einzelnen faktoren gezählt und addiert (bin bei der gesamtgleichung) |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 06. Dez 2006 00:23 Titel: |
|
|
Puh, ich glaube, anders als schrittweise dürfte das schwierig werden.
Vielleicht magst du dir mal zum Vergleich folgenden Thread anschauen, da haben wir neulich etwas ganz ähnliches für einen gedämpften elektrischen Schwingkreis gemacht. Da kannst du ein bisschen sehen, wie man weitermachen kann, wenn man alles in die DGL eingesetzt hat.
http://www.physikerboard.de/ltopic,7011,0,asc,0.html |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 06. Dez 2006 00:24 Titel: |
|
|
wenigstens ein bisschen zusammengefasst:
^2 * 2*[ e^{- \frac{\gamma}{2}*t}*cos(wt)]+ 2*[(-\frac{\gamma}{2})*e^{- \frac{\gamma}{2}*t}*w*(-sin(wt))] + e^{- \frac{\gamma}{2}*t}*w^2*(-cos(wt))+ \gamma*x_0*-\frac{\gamma}{2}* e^{- \frac{\gamma}{2}*t}*cos(wt)+e^{- \frac{\gamma}{2}*t}*w*(sin(wt))+w_0^2*x_0*e^{- \frac{\gamma}{2}*t}*cos(wt) ) |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 06. Dez 2006 00:26 Titel: |
|
|
Soll das schon nach dem Einsetzen in die DGL sein?
Dann würde ich eine Gleichung erwarten, keinen Term. |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 06. Dez 2006 00:30 Titel: |
|
|
|
= 0 |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 06. Dez 2006 00:35 Titel: |
|
|
Okay, helfen dir nun die Tipps aus dem anderen Thread zum elektrischen gedämpften Schwingkreis?
* Also auf beiden Seiten durch den e-hoch-Term teilen, dann verschwindet der.
* cos-Terme auf die eine Seite, sin auf die andere
* sin bzw cos ausklammern.
* Die Klammern beide Null setzen, damit die Gleichung erfüllt werden kann.
* Daraus die Dämpfungskonstante und die Kreisfrequenz bestimmen. |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 06. Dez 2006 00:36 Titel: |
|
|
also ich rechne jetzt mal un poste dir meine lösung (und du hast sie wahrscheinlich schon )
auf beiden seiten durch den e-term?? ich hab doch nur eine seite wo der vorkommt... |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 06. Dez 2006 00:43 Titel: |
|
|
Na, auf der rechten Seite ist Null durch irgendwas ja wieder Null.
Tipp zum Ergebnis: Das wird dieselbe Form haben wie das, was im elektrischen Fall herausgekommen ist. Vielleicht kommt dir das Endergebnis dann auch aus deinen Büchern bekannt vor |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 06. Dez 2006 00:47 Titel: |
|
|
|
hab jetzt cosin auf einer und sin auf der andren seite, e habe ich gekürzt, das mit dem ausklammern was genau? nur den cos oder cos(wt)?? |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 06. Dez 2006 00:52 Titel: |
|
|
Das cos(wt).
Zuletzt bearbeitet von dermarkus am 06. Dez 2006 01:01, insgesamt einmal bearbeitet |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 06. Dez 2006 00:57 Titel: |
|
|
|
und jetzt? |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 06. Dez 2006 01:10 Titel: |
|
|
beim 1. (cos)
erhalte ich
und auf der andren seite w=0 |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 06. Dez 2006 01:21 Titel: |
|
|
Die Lösung w=0 ist nicht die allgemeine Lösung, die du suchst. Was gibt dir die Gleichung aus der Klammer für den Sinus für ein Ergebnis für die Dämpfungskonstante, wenn du diese Gleichung auf beiden Seiten durch w teilst?
Was bekommst du folglich als Lösung für w aus der Gleichung aus der Klammer für den cos? |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 06. Dez 2006 01:31 Titel: |
|
|
schau bitte zuerst ob die ausklammerung stimmt, bitte:
 * [x_0*(- (\frac{\gamma}{2}))^2-w^2+\gamma*x_0*(- (\frac{\gamma}{2}))+w_0^2*x_0 )
=
*[- (\frac{\gamma}{2})*w- (\frac{\gamma}{2})*w+w] )
für w bekomme ich 0, für gamma = 1 |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 06. Dez 2006 02:00 Titel: |
|
|
Wenn ich mich jetzt um diese Uhrzeit nicht verrechnet habe, dann bekomme ich für die Klammer am Cosinus dasselbe wie du,
und für die Klammer am Sinus bekomme ich Null, egal wie groß omega und gamma sind. (Die Klammer am Sinus bringt hier also keine zusätzliche Information)
Das bedeutet, du kannst, indem du die Klammer am Cosinus Null setzt, eine Beziehung aufstellen, mit der du omega in Abhängigkeit von \omega_0 und gamma ausdrücken kannst; das ist dann deine Lösung für omega. |
|
|
MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 06. Dez 2006 02:03 Titel: |
|
|
hast du beim sinus wirklich null in der klammer?  was hab ich denn da falsch gemacht? oder hast du da omega drin stehen, dann habe ich nämlich einen vorzeichenfehler...
zu der cos klammer: bringt es was, dort x_0 auszuklammern oder wäre ich mit gamma besser bedient? oder gar nicht ausklammern?? |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 06. Dez 2006 02:08 Titel: |
|
|
| MCF hat Folgendes geschrieben: | hast du beim sinus wirklich null in der klammer? was hab ich denn da falsch gemacht? oder hast du da omega drin stehen, dann habe ich nämlich einen vorzeichenfehler...
|
Ich vermute, du hast bei deinem dritten Term in der Klammer ein gamma vergessen, das dir beim Ableiten irgendwo abhanden gekommen ist.
| Zitat: |
zu der cos klammer: bringt es was, dort x_0 auszuklammern oder wäre ich mit gamma besser bedient? oder gar nicht ausklammern?? |
Ja, das x_0 klammerst du aus, die restliche Klammer setzt du Null, und dann hast du auch schon nach kurzem Umformen das Ergebnis.
 |
|
|
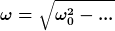MCF
Anmeldungsdatum: 04.12.2006
Beiträge: 52
|
| MCF Verfasst am: 06. Dez 2006 02:12 Titel: |
|
|
musste mir nochmal genau sagen, wo ich mein gamma verloren hab...
... wurzel [w_0 - (3gamma^2) / 4] ???? |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 06. Dez 2006 02:16 Titel: |
|
|
Das muss irgendwo gewesen sein, als du beim Ableiten vergessen hast, eine innere Ableitung mit nach vorne zu nehmen.
Oder hast du vielleicht beim Einsetzen von x' vergessen, dass da in der DGL noch ein gamma davorsteht?
--------------
Ich glaube, du bist jetzt so nahe dran, dass du es nun selbst hinbekommen kannst Und ich verkrieche mich in mein Bett, damit morgen auch noch ein Tag ist  |
|
|
|
Registrieren
Login
FAQ
Suchen
