| Autor |
Nachricht |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 12:12 Titel: Harmonischer Oszillator und Störungstheorie Sasquat Verfasst am: 28. Jul 2019 12:12 Titel: Harmonischer Oszillator und Störungstheorie |
 |
|
Meine Frage:
Betrachten Sie eine lineareStörung des harmonischen Oszillators, wie folgt:
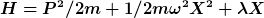
Berechnen Sie die erste nichtverschwindende Korrektur zu den Energieeigenwerten des un-gestörten harmonischen Oszillators mit Hilfe von Störungstheorie.
Meine Ideen:
Ich habe für diese Aufgabe eine Lösung bei der ich jedoch probleme hab sie zu verstehen. Als erstes kann man die Störung mit den Leiteroperatoren ausdrücken:
)
In erster Ordunung gilt ja dann
}=\frac{\lambda x_{0}}{\sqrt{2}}\left< n |(a+a^{t})| n \right> )
Dies ist null weil wir ja nicht die gleiche Anzahl an Erzeugungs und Vernichtungsoperatoren haben oder? Und so somit die Brakets zusammen null sind.
In zweiter Ordnung gilt:
}=(\frac{\lambda x_{0}}{\sqrt{2}})^{2}\sum\limits_{n\neq m}^n \frac{|\left< n |a+a^{t}| n \right>|^{2}}{E_{n}- E_{m} } )
Wenn ich es richtig Verstanden hab dann steht im Betrag am Ende n+1+n=2n+1 ich weiß aber einfach nicht was mit den Energien unter dem Bruch passiert. In der Musterlösung steht einfach das
}=- \frac{\lambda^{2}x_{0}^2}{2\omega hquer} )
aber verstehe nicht wieso. Danke im Vorraus für jede Hilfe.
Korrektur aus zweitem Beitrag übernommen, diesen gelöscht, damit es nicht so aussieht, als ob schon jemand antwortet. Steffen |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 12:59 Titel: index_razor Verfasst am: 28. Jul 2019 12:59 Titel: |
 |
|
Die 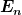 sind die Energieeigenwerte des ungestörten harmonischen Oszillators sind die Energieeigenwerte des ungestörten harmonischen Oszillators

Setze dies mal in den Korrekturterm 2. Ordnung ein. |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 14:56 Titel: Sasquat Verfasst am: 28. Jul 2019 14:56 Titel: |
 |
|
Ich sehe zwar jetzt woher das hquer omega in der Lösung kommt aber ich verstehe nicht ganz was dann  ist. Wieso ist die Lösung auch negativ? ist. Wieso ist die Lösung auch negativ? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 15:38 Titel: index_razor Verfasst am: 28. Jul 2019 15:38 Titel: |
 |
|
Vielleicht ist das Problem, daß du den Term 2. Ordnung falsch hingeschrieben hast. Ich dachte erst das wäre ein bloßer Tippfehler. Da muß stehen
}_n = \lambda^2 \sum_{m\neq n}\frac{|\langle n| X| m\rangle|^2}{E_n - E_m})
die Summe geht über m. Nun setze noch mal alles ein. |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 15:48 Titel: Sasquat Verfasst am: 28. Jul 2019 15:48 Titel: |
 |
|
Es ist
}=(\frac{\lambda x_{0}}{\sqrt{2}})^{2}\sum\limits_{n\neq m}^n \frac{|\left< n |a+a^{t}| m \right>|^{2}}{E_{n}- E_{m} } )
Wenn ich nun einsetze habe ich:
}=(\frac{\lambda x_{0}}{\sqrt{2}})^{2}\sum\limits_{n\neq m}^n \frac{\left< n |a^2+aa^{t}+a^{t}a+(a^{t})^2| m \right>}{ hquer\omega n- E_{m} } )
Ist dies richtig? und wenn ja was mach ich als nächstes? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 15:53 Titel: index_razor Verfasst am: 28. Jul 2019 15:53 Titel: |
 |
|
|
Nein, das ist nicht richtig. Schreib dir mal ein paar Summanden explizit hin, also sagen wir für m=0,1,2... Wie sehen die einzelnen Summanden aus? |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 15:56 Titel: Sasquat Verfasst am: 28. Jul 2019 15:56 Titel: |
 |
|
|
Um ehrlich zu sein bin ich verwirrt was mach ich mit zB E0? Ist das einfach null? und E1 ist dann hquer omega? Und wende ich die Operatoren dann bei 0 und 1 etc alle einmal an? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 16:01 Titel: index_razor Verfasst am: 28. Jul 2019 16:01 Titel: |
 |
|
| Sasquat hat Folgendes geschrieben: | | Um ehrlich zu sein bin ich verwirrt was mach ich mit zB E0? Ist das einfach null? |
Nein, das ist nicht null. Ich würde gern sehen, wie du darauf kommst. Die Korrekturen sind unabhängig von n. |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 16:03 Titel: Sasquat Verfasst am: 28. Jul 2019 16:03 Titel: |
 |
|
|
Ich meine unter dem Bruch wenn En definiert ist als n hquer omega dann ist für 0 doch das Em in diesem fall Null oder? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 16:06 Titel: index_razor Verfasst am: 28. Jul 2019 16:06 Titel: |
 |
|
| Sasquat hat Folgendes geschrieben: | | Ich meine unter dem Bruch wenn En definiert ist als n hquer omega dann ist für 0 doch das Em in diesem fall Null oder? |
Im Nenner steht ein 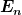 und ein anderes und ein anderes  ( ( ). Nur eins davon kann null sein. Schreib doch mal die ersten beiden Terme der Summe, von mir aus für n=0, hin. ). Nur eins davon kann null sein. Schreib doch mal die ersten beiden Terme der Summe, von mir aus für n=0, hin. |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 16:09 Titel: Sasquat Verfasst am: 28. Jul 2019 16:09 Titel: |
 |
|
|
Ich verstehe eine Sache nicht wenn wir sagen n=0 ist dann m zB 1? Es kann ja nicht auch null sein. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 16:10 Titel: index_razor Verfasst am: 28. Jul 2019 16:10 Titel: |
 |
|
| Sasquat hat Folgendes geschrieben: | | Ich verstehe eine Sache nicht wenn wir sagen n=0 ist dann m zB 1? Es kann ja nicht auch null sein. |
Ja, das stimmt. Und wo ist das Problem dabei? |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 16:17 Titel: Sasquat Verfasst am: 28. Jul 2019 16:17 Titel: |
 |
|
}=(\frac{\lambda x_{0}}{\sqrt{2}})^{2}\sum\limits_{n\neq m} \frac{\left< 0 |a^2+aa^{t}+a^{t}a+(a^{t})^2| 1 \right>}{ 0-hquer\omega } )
Nun kann ich ja die Operatoren anwenden aber ich kriege bei allen null raus da das Braket nicht die gleiche Zahl hat. Was mache ich falsch? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 16:22 Titel: index_razor Verfasst am: 28. Jul 2019 16:22 Titel: |
 |
|
Der Zähler ^2| 1 \right>) stimmt nicht. Das muß stimmt nicht. Das muß

heißen. Bei dir steht
 . . |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 16:23 Titel: Sasquat Verfasst am: 28. Jul 2019 16:23 Titel: |
 |
|
|
Ich weiß leider nicht wie sich das Quadrat auf das ganze Braket auswirkt. Könntest du mir das erklären? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 16:27 Titel: index_razor Verfasst am: 28. Jul 2019 16:27 Titel: |
 |
|
Für eine komplexe z Zahl gilt: 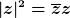 , wobei , wobei  komplex-konfigiert zu komplex-konfigiert zu  ist. Das bedeutet ist. Das bedeutet
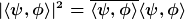 . .
Das heißt, du berechnest  , bildest das komplex-konjugierte und multiplizierst beides. , bildest das komplex-konjugierte und multiplizierst beides. |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 16:33 Titel: Sasquat Verfasst am: 28. Jul 2019 16:33 Titel: |
 |
|
Ist dies schonmal richtig?
 |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 16:37 Titel: index_razor Verfasst am: 28. Jul 2019 16:37 Titel: |
 |
|
|
Fast. Nach dem ersten '=' scheint aus einer Addition aber plötzlich eine Multiplikation geworden zu sein. |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 16:40 Titel: Sasquat Verfasst am: 28. Jul 2019 16:40 Titel: |
 |
|
|
Mein Fehler Also steht dort am Ende 1+0 was mit sich selbst multipliziert auch eins ist richtig? Und das endergebniss ist dann das Gleiche wie die Musterlösung. Wie macht man dies nun Allgemein? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 16:44 Titel: index_razor Verfasst am: 28. Jul 2019 16:44 Titel: |
 |
|
Im allgemeinen berechnest du erstmal
 . .
Dazu mußt du dir überlegen, für welche Werte von m da etwas von null verschiedenes rauskommen kann. |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 16:56 Titel: Sasquat Verfasst am: 28. Jul 2019 16:56 Titel: |
 |
|
|
Es geht ja nur wenn n=m+1 oder m-1 da wir um einen aufsteigen oder absteigen. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 16:59 Titel: index_razor Verfasst am: 28. Jul 2019 16:59 Titel: |
 |
|
|
Ja, und was kommt dann raus? |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 17:06 Titel: Sasquat Verfasst am: 28. Jul 2019 17:06 Titel: |
 |
|
}=(\frac{\lambda x_{0}}{\sqrt{2}})^{2}\sum\limits_{n\neq m} \frac{|\left< n |\sqrt{m}| m-1 \right>+\left< n |\sqrt{m+1}| m+1 \right>|^2}{ hquer\omega n-hquer\omega m } )
Jetzt muss ich das ganze noch miteinander multiplizieren aber ich bin mir unsicher wie das geht. Was passiert mit den Brakets? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 17:20 Titel: index_razor Verfasst am: 28. Jul 2019 17:20 Titel: |
 |
|
Die kannst du bereits explizit ausrechnen. Es handelt sich bei 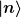 etc. um die Eigenzustände des ungestörten Hamiltonoperators. Diese sind orthogonal und normiert, also gilt etc. um die Eigenzustände des ungestörten Hamiltonoperators. Diese sind orthogonal und normiert, also gilt

Wenn dir das alles nicht klar ist, solltest du unbedingt nochmal die Grundlagen etwas auffrischen.
Übrigens, das Latex-Kommando für 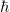 ist . ist . |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 17:33 Titel: Sasquat Verfasst am: 28. Jul 2019 17:33 Titel: |
 |
|
Also gilt:

und somit

ist dies dann einfach
 \delta_{nm+1}} { \hbar \omega n - \hbar \omega m} )
Das kann aber nicht richtig sein oder? Das ganze sollte sich ja wegkürzen tut es aber nicht. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 17:40 Titel: index_razor Verfasst am: 28. Jul 2019 17:40 Titel: |
 |
|
| Sasquat hat Folgendes geschrieben: |

ist dies dann einfach
 \delta_{nm+1}} { \hbar \omega n - \hbar \omega m} )
Das kann aber nicht richtig sein oder? |
Ist es auch nicht. Wie kommst du darauf? Bleib mal bei diesem Ausdruck

Und denk daran: Dieser steht unter einer Summe über m. Schreib dir einfach mal ein paar Summanden mit expliziten Werten für m hin. Dann überlege dir welche davon stehen bleiben. |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 17:45 Titel: Sasquat Verfasst am: 28. Jul 2019 17:45 Titel: |
 |
|
|
Okay ich bin wieder verwirrt wie kann ich wissen welche stehen bleiben wenn ich nicht weiß was n ist? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 17:54 Titel: index_razor Verfasst am: 28. Jul 2019 17:54 Titel: |
 |
|
Es bleiben Terme stehen, in denen m jeweils eins kleiner oder eins größer als n ist. Das hast du gerade ausgerechnet.
Wenn z.B. m = n-2 wäre, dann wäre sowohl  als auch als auch 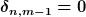 . . |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 17:57 Titel: Sasquat Verfasst am: 28. Jul 2019 17:57 Titel: |
 |
|
|
Kann ich mir dann nicht einfach die zwei Fälle angucken wo ich für n m+1 und m-1 einsetze? Aber das scheint auch nicht das richtige Ergebniss zu liefern. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 17:59 Titel: index_razor Verfasst am: 28. Jul 2019 17:59 Titel: |
 |
|
n ist fix. Über m wird summiert.
Was heißt "es scheint nicht das richtige Ergebnis zu liefern"? Hast du das ausgerechnet? Wenn ja, wie sieht die Rechnung aus? |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 18:04 Titel: Sasquat Verfasst am: 28. Jul 2019 18:04 Titel: |
 |
|
|
Sagen wir mal m=n-1 dann ist der zweite Term über dem Bruch nicht null. Wenn man für m nun n-1 einsetzt steht dort wurzel n und dies zum quadrat also einfach n. Unter dem Bruch kann man das h und das omega ausklammern und erhält n-(n-1)=1 also steht am ende n/1=n dort. Ist dies Falsch? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 18:09 Titel: index_razor Verfasst am: 28. Jul 2019 18:09 Titel: |
 |
|
Das klingt zumindest erstmal richtig. Es beschreibt aber noch nicht alle Korrekturterme zum n-ten Eigenwert.
Es wäre übrigens leichter zu prüfen, wenn du Formeln hinschreiben würdest. |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 18:11 Titel: Sasquat Verfasst am: 28. Jul 2019 18:11 Titel: |
 |
|
|
Was genau meinst du mit es beschreibt noch nicht alle Korrekturterme? Was muss ich noch machen? |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 18:13 Titel: Sasquat Verfasst am: 28. Jul 2019 18:13 Titel: |
 |
|
|
Ohh weil es eine Summe ist muss ich auch noch den Wert für m=n+1 berechnen der -n-1 ist und somit hat man dann n-n-1 was -1 ist und das ist dann die Musterlösung. Ist das Richtig? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 18:13 Titel: index_razor Verfasst am: 28. Jul 2019 18:13 Titel: |
 |
|
|
m=n-1 ist nicht der einzige von null verschiedene Term. Es gibt noch einen anderen. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2019 18:14 Titel: index_razor Verfasst am: 28. Jul 2019 18:14 Titel: |
 |
|
| Sasquat hat Folgendes geschrieben: | | Ohh weil es eine Summe ist muss ich auch noch den Wert für m=n+1 berechnen der -n-1 ist und somit hat man dann n-n-1 was -1 ist und das ist dann die Musterlösung. Ist das Richtig? |
Ja, das klingt richtig. |
|
 |
Sasquat
Gast
|
 Sasquat Verfasst am: 28. Jul 2019 18:14 Titel: Sasquat Verfasst am: 28. Jul 2019 18:14 Titel: |
 |
|
|
Okay Vielen Dank für die Geduld ich hab es jetzt endlich verstanden. |
|
 |
|















