| Autor |
Nachricht |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Feb 2017 20:47 Titel: Harmonischer Oszillator Max Cohen Verfasst am: 11. Feb 2017 20:47 Titel: Harmonischer Oszillator |
 |
|
Hallo, ich habe die Aufgabe:
a) Wir betrachten einen harmonischen Oszillator mit dem Potential =\frac{1}{2}m\omega^2x^2)
Berechne den Wert für  unter ader Annahme, dass unter ader Annahme, dass =Axe^{-\alpha x^2}) eine Lösung der SG ist und bestimme den Energieeigenwert eine Lösung der SG ist und bestimme den Energieeigenwert 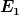
b) Ein harmonischer Oszillator befinde sich zum Zeitpunkt  im Zustand im Zustand
\rangle=\frac{1}{2}(|0\rangle+e^{i\phi}|1\rangle))
berechne den Ortserwartungswert von  als Funktion von als Funktion von 
Meine Idee:
a) Ich habe die Wellenfunktion in die SG eingesetzt. Es gilt:

=E\phi(x))
-4\alpha\phi_1(x)-2\alpha\phi_1(x)]+\frac{1}{2}m\omega^2x^2\phi_1(x)=E\phi_1(x))

Ist das bereits der Energieeigenwert?
Das Ganze kann ich auch nach  auflösen. auflösen.
Das wäre dann der Aufgabenteil a)?
b) Hier habe ich noch keine Idee. Ich weiß das gilt 
Ich weiß allerdings nicht wie ich damit weiter rechne.
Kann mir jemand helfen?
Danke! |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Feb 2017 20:57 Titel: Re: Harmonischer Oszillator jh8979 Verfasst am: 11. Feb 2017 20:57 Titel: Re: Harmonischer Oszillator |
 |
|
| Max Cohen hat Folgendes geschrieben: |

|
Nein, der Energieeigenwert ist ja eine feste Zahl (mit Einheiten) und kann somit nicht von x abhängen. |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Feb 2017 21:26 Titel: Max Cohen Verfasst am: 11. Feb 2017 21:26 Titel: |
 |
|
Hallo, bin ich bei der Bestimmung von 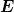 und und  falsch vorgegangen oder ist es ein Rechenfehler meinerseits? falsch vorgegangen oder ist es ein Rechenfehler meinerseits?
b) Kannst du mir sagen wie ich den Teil am besten löse?
Gruß |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Feb 2017 21:28 Titel: jh8979 Verfasst am: 11. Feb 2017 21:28 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | Hallo, bin ich bei der Bestimmung von 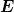 und und  falsch vorgegangen oder ist es ein Rechenfehler meinerseits? falsch vorgegangen oder ist es ein Rechenfehler meinerseits?
|
Rechenfehler weiss ich nicht, die Idee ist schon richtig. |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Feb 2017 21:51 Titel: Max Cohen Verfasst am: 11. Feb 2017 21:51 Titel: |
 |
|
Wie kann ich denn sonst das  und den Energieeigenwert und den Energieeigenwert 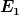 bestimmen? bestimmen?
Ich habe auch noch einmal nachgerechnet. Ich erhalte für die Ableitung =\phi_1(x)[8\alpha^2x+4\alpha^2x^2-2\alpha])
Gruß! |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Feb 2017 21:54 Titel: Re: Harmonischer Oszillator jh8979 Verfasst am: 11. Feb 2017 21:54 Titel: Re: Harmonischer Oszillator |
 |
|
| jh8979 hat Folgendes geschrieben: | | der Energieeigenwert ... kann somit nicht von x abhängen. |
Kann man vllt alpha so wählen? |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Feb 2017 22:00 Titel: Max Cohen Verfasst am: 11. Feb 2017 22:00 Titel: |
 |
|
Einfach wählen? Ich glaube das darf ich nicht.
Zumindest steht in der Aufgabe das man diesen Wert berechnen soll.
Angenommen ich würde  wählen, wie komme ich dann an den Energieeigenwert? wählen, wie komme ich dann an den Energieeigenwert?
b) Kannst du mir einen Tipp geben damit ich überhaupt irgendwo ansetzen kann? Ich stehe momentan noch komplett auf dem Schlauch.
Gruß |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Feb 2017 22:01 Titel: jh8979 Verfasst am: 11. Feb 2017 22:01 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | Einfach wählen? Ich glaube das darf ich nicht.
Zumindest steht in der Aufgabe das man diesen Wert berechnen soll. |
ach so ...
| Zitat: |
Angenommen ich würde  wählen, wie komme ich dann an den Energieeigenwert? wählen, wie komme ich dann an den Energieeigenwert? |
Vllt hängt das ja sogar zusammen....verrückt... |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Feb 2017 22:06 Titel: Max Cohen Verfasst am: 11. Feb 2017 22:06 Titel: |
 |
|
Entweder willst du mich trollen oder du möchtest mir nicht helfen.
Hat vielleicht jemand anderes einen Tipp für mich? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Feb 2017 22:07 Titel: jh8979 Verfasst am: 11. Feb 2017 22:07 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | Entweder willst du mich trollen oder du möchtest mir nicht helfen.
|
Oder Du solltest mal über meine Antworten nachdenken... wer weiss das schon... so viele Möglichkeiten... |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Feb 2017 22:17 Titel: Max Cohen Verfasst am: 11. Feb 2017 22:17 Titel: |
 |
|
Arrogant und Selbstherrlich sage ich zu deinen Hilfestellungen nur. Wenn du als Moderator die Stütze und erste Anlaufstelle bist dann läuft hier etwas gewaltig schief.
Ich hoffe das mir jemand anderes noch kompetent helfen kann und nicht sollch einen Rotz als Hilfestellung verkauft.
Danke! |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Feb 2017 22:21 Titel: jh8979 Verfasst am: 11. Feb 2017 22:21 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | ... dann läuft hier etwas gewaltig schief.
|
Seh ich aus meiner Warte genauso... Meine Antwort sagt Dir alles was Du wissen musst.
PS: Löscht Du die Frage und Deine Posts eigentlich wieder, wenn sie endgültig beantwortet wurden? Rein interessehalber.... |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 11. Feb 2017 22:24 Titel: TomS Verfasst am: 11. Feb 2017 22:24 Titel: |
 |
|
@ Mac Cohen: Ich verstehe den Ärger nicht.
Der Wert von Alpha ist geeignet zu bestimmen. Das steht so in der Aufgabe, und darauf hat jh8979 hingewiesen (und die Gleichungen stehen bereits da).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Feb 2017 22:44 Titel: Max Cohen Verfasst am: 11. Feb 2017 22:44 Titel: |
 |
|
Hallo TomS, in der Aufgabe steht das man  berechnen soll. Wie soll man den Wert für berechnen soll. Wie soll man den Wert für  geeignet bestimmen, was ist damit gemeint? geeignet bestimmen, was ist damit gemeint?
Ich habe nochmal nachgerechnet.
=\phi_1(x)[12\alpha^2x^2-2\alpha])

Ich habe das Ganze einmal umgestellt.

Hier könnte ich die Nullstellen und somit die Werte für  bestimmen. Es sind dann allerdings zwei Werte und von diesen den "sinnvollen" Wert für bestimmen. Es sind dann allerdings zwei Werte und von diesen den "sinnvollen" Wert für  auswählen. auswählen.
Ist das so gemeint? Dann fehlt allerdings immer noch der Energieeigenwert.
Grüße! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 11. Feb 2017 22:54 Titel: TomS Verfasst am: 11. Feb 2017 22:54 Titel: |
 |
|
Ich skizziere mal deinen (richtigen) Ansatz; deine Rechnung oben liefert
 = f_\alpha(x)\,\phi_\alpha(x))
Gesucht ist jedoch
 = E\,\phi_\alpha(x))
D.h. es muss gelten
 = E = \text{const.})
Siehst du jetzt, wie's weitergeht?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Feb 2017 23:09 Titel: Max Cohen Verfasst am: 11. Feb 2017 23:09 Titel: |
 |
|
Ok,  muss so gewählt werden, dass die Energie Konstant ist. Beim harmonischen Oszillator sind die Energien muss so gewählt werden, dass die Energie Konstant ist. Beim harmonischen Oszillator sind die Energien )

Jetzt eingesetzt und nun die Nullstellen berechnen?

b) Für den Ortserwartungswert gilt erstmal:
|x|\phi(t=0)\rangle dx=\int_{-\infty}^{\infty}x|\phi(t=0)|^2 dx)
Wenn ich das alles einsetze erhalte ich allerdings ein Integral über x das nicht konvergiert.
Grüße! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 12. Feb 2017 10:09 Titel: TomS Verfasst am: 12. Feb 2017 10:09 Titel: |
 |
|
Ich weiß nicht, was du da rechnest.
Du hast oben bereits alles hingeschrieben:
+\frac{1}{2}m\omega^2x^2\right]\,\phi_1 = E\,\phi_1)
Links steht zunächst die Funktion f
 = f_\alpha(x)\,\phi_\alpha(x))
Gesucht ist jedoch eine Eigenfunktion
 = E\,\phi_\alpha(x))
D.h. die Ortsabhängigkeit muss verschwinden
 = E = \text{const.})
Also muss

gelten. |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 12. Feb 2017 11:19 Titel: Max Cohen Verfasst am: 12. Feb 2017 11:19 Titel: |
 |
|
Ok, die Ortsabhängigkeit ist genau dann Null, wenn 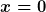 gilt oder gilt oder 
So passt das nun?
Grüße! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 12. Feb 2017 12:32 Titel: TomS Verfasst am: 12. Feb 2017 12:32 Titel: |
 |
|
Ortsunabhängigkeot für genau ein x ist sinnlos.
alpha muss einen ganz bestimmten Wert haben, dann und nur dann liefert der o.g. Ansatz eine Eigenfunktion. Und die Eigenschaften der Auf- und Absteigeoperatoren stellen sicher, dass dieses alpha auch für andere n=0,2,3,... die korrekte Wahl ist.
Damit hast du zu (a) den richtigen Wert von alpha; jetzt benötigst du noch den Energieeigenwert. |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 12. Feb 2017 13:18 Titel: Max Cohen Verfasst am: 12. Feb 2017 13:18 Titel: |
 |
|
Den erhalte ich vermutlich nicht indem ich mein  hier einsetze da der Energieeigenwert immer noch x-abhängig ist. hier einsetze da der Energieeigenwert immer noch x-abhängig ist.

Warum ist der Energieeigenwert nicht  ? ?
Gruß! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 12. Feb 2017 17:22 Titel: TomS Verfasst am: 12. Feb 2017 17:22 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | Den erhalte ich vermutlich nicht indem ich mein  hier einsetze da der Energieeigenwert immer noch x-abhängig ist. hier einsetze da der Energieeigenwert immer noch x-abhängig ist.
 |
Warum glaubst du nicht, dass der Energieeigenwert daraus folgt? Für das von dir o.g. alpha verschwindet doch die x-Abhängigkeit.
Und grundsätzlich: es gibt keinen x-abhängigen Eigenwert! Wenn die x-Abhängigkeit nicht verschwinden würde, dann läge kein Eigenwert vor; das ist letztlich eine reine Definitionssache.
| Max Cohen hat Folgendes geschrieben: | Warum ist der Energieeigenwert nicht  ? ? |
Wer sagt, dass das nicht der Fall sein sollte?
Natürlich muss dieses Ergebnis aus deinem Ansatz folgen; du darfst es nur nicht hineinstecken. |
|
 |
hoher Preis
Gast
|
 hoher Preis Verfasst am: 12. Feb 2017 18:29 Titel: hoher Preis Verfasst am: 12. Feb 2017 18:29 Titel: |
 |
|
kann man überhaupt ein H-Atom als harmonischer Oszillator betrachten (beschreiben)?
Gibt es da Probleme? |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 12. Feb 2017 19:11 Titel: Max Cohen Verfasst am: 12. Feb 2017 19:11 Titel: |
 |
|
Ich check's nicht. Wenn ich  einsetze erhalte ich: einsetze erhalte ich:
 Das ist doch eindeutig x-abhängig. Das ist doch eindeutig x-abhängig. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 12. Feb 2017 20:15 Titel: TomS Verfasst am: 12. Feb 2017 20:15 Titel: |
 |
|
Nein, ist es nicht
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 12. Feb 2017 20:20 Titel: TomS Verfasst am: 12. Feb 2017 20:20 Titel: |
 |
|
Aber mit dem anderen Term stimmt irgendwas nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 13. Feb 2017 11:56 Titel: Max Cohen Verfasst am: 13. Feb 2017 11:56 Titel: |
 |
|
Hallo Tom, schonmal danke für deine Hilfe. Ich habe noch eine Frage zu der b)
Meine Idee dazu ist die folgende:
|^2dx=\int_{-\infty}^{\infty}xdx) erhalte ich hier aufgrund der Orthonormiertheit der Wellenfunktionen. Das Integral ist allerdings so nicht berechenbar. Ich habe mir auch die zugehörigen WF einmal rausgesucht. erhalte ich hier aufgrund der Orthonormiertheit der Wellenfunktionen. Das Integral ist allerdings so nicht berechenbar. Ich habe mir auch die zugehörigen WF einmal rausgesucht.
^{1/4}e^{-\frac{\alpha}{2}x^2})
^{3/4}\sqrt{2}\sqrt{\alpha}xe^{-\frac{\alpha x^2}{2}})
Das wäre noch eine weitere Idee um das Integral auszuwerten.
Was habe ich denn hier falsch gemacht?
Andererseits ist natürlich |^2) eine gerade Funktion und eine gerade Funktion und  eine ungerade Funktion. Das Produkt ist demnach eine ungerade Funktion. Das heißt also das eine ungerade Funktion über ein symmetrisches Intervall integriert wird. Damit muss Null herauskommen. Ist das des Rätsels Lösung? eine ungerade Funktion. Das Produkt ist demnach eine ungerade Funktion. Das heißt also das eine ungerade Funktion über ein symmetrisches Intervall integriert wird. Damit muss Null herauskommen. Ist das des Rätsels Lösung?
Andererseits wenn die Varianz  berechnet wird erhält man schlussendlich das Integral berechnet wird erhält man schlussendlich das Integral  was ebenfalls Null ergibt und das wäre jede Potenz von was ebenfalls Null ergibt und das wäre jede Potenz von  . Das kann doch nicht sein ... . Das kann doch nicht sein ...
Grüße! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 13. Feb 2017 22:39 Titel: TomS Verfasst am: 13. Feb 2017 22:39 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | Meine Idee dazu ist die folgende:
|^2dx=\int_{-\infty}^{\infty}xdx) |
Das zweite Gleichheitszeichen ist falsch. Wieso sollte das Absolutquadrat der Wellenfunktion wegfallen?
| Max Cohen hat Folgendes geschrieben: | Ich habe mir auch die zugehörigen WF einmal rausgesucht.
^{1/4}e^{-\frac{\alpha}{2}x^2})
^{3/4}\sqrt{2}\sqrt{\alpha}xe^{-\frac{\alpha x^2}{2}}) |
Die Wellenfunktion ist nicht mit dem Zustand identisch, sie entspricht der Projektion des Zustandes auf Ortseigenzustände.
 = \langle x|0\rangle = (\frac{\alpha}{\pi})^{1/4}e^{-\frac{\alpha}{2}x^2})
| Max Cohen hat Folgendes geschrieben: | Andererseits wenn die Varianz  berechnet wird erhält man schlussendlich das Integral berechnet wird erhält man schlussendlich das Integral  was ebenfalls Null ergibt und das wäre jede Potenz von was ebenfalls Null ergibt und das wäre jede Potenz von  . Das kann doch nicht sein ... . Das kann doch nicht sein ... |
Selben Fehler wie oben; es gilt
 \rangle = \int_{-\infty}^{+\infty}dx\,f(x)\,|\phi(x)|^2)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 13. Feb 2017 23:43 Titel: Max Cohen Verfasst am: 13. Feb 2017 23:43 Titel: |
 |
|
Hallo, ich dachte es gilt:
|^2=\phi^*(t=0)\phi(t=0)=\frac{1}{2}(|0\rangle+e^{-i\phi}|1\rangle)\frac{1}{2}(|0\rangle+e^{i\phi}|1\rangle))
Aufgrund der Orthonormiertheit bleibt dann nur übrig:
=\frac{1}{2})
Damit dann also ...
Das scheint allerdings falsch zu sein. Wie kann ich den Erwartungswert denn korrekt berechnen?
Grüße! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 14. Feb 2017 00:31 Titel: TomS Verfasst am: 14. Feb 2017 00:31 Titel: |
 |
|
Jetzt vergiss erst mal bras und kets, die hast du offensichtlich nicht verstanden.
Wie soll denn bitte

gelten, wenn

gilt.
Lediglich für das Integral gilt

Ich schlage dir ernsthaft vor, nochmal über "Los" zu gehen und die Grundlagen durchzuarbeiten. |
|
 |
|















