| Autor |
Nachricht |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 08. Nov 2015 17:08 Titel: Harmonischer Oszillator Max Cohen Verfasst am: 08. Nov 2015 17:08 Titel: Harmonischer Oszillator |
 |
|
##########
Zuletzt bearbeitet von Max Cohen am 11. Nov 2015 23:20, insgesamt einmal bearbeitet |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 08. Nov 2015 20:22 Titel: Re: Harmonischer Oszillator jh8979 Verfasst am: 08. Nov 2015 20:22 Titel: Re: Harmonischer Oszillator |
 |
|
| Max Cohen hat Folgendes geschrieben: |
Hallo zusammen,
Ich soll zeigen dass der angetriebene harmonische Oszillator
)
im stationären Zustand keine Energie hinzugewinnt das heißt keine Leistung aus dem antreibenden Feld absorbiert wenn er ungedämpft ist also wenn 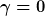 . .
Wenn 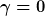 vereinfacht sich die DGL zu: vereinfacht sich die DGL zu:
)
Ich bin mir ehrlich gesagt garnicht sicher ob nun die DGL gelöst werden soll oder ob man das anders zeigen muss. Hat jemand eine Idee?
|
[jh8979: Da Du es für eine gute Idee hieltest, Deinen Urspungspost nach Tagen zu löschen, hielt ich es für eine gute Idee ihn hier wieder herzustellen. LG]
| Max Cohen hat Folgendes geschrieben: |
Ich bin mir ehrlich gesagt garnicht sicher ob nun die DGL gelöst werden soll oder ob man das anders zeigen muss. Hat jemand eine Idee? |
Das wäre eine Möglichkeit das Problem anzugehen.
Zuletzt bearbeitet von jh8979 am 12. Nov 2015 00:19, insgesamt einmal bearbeitet |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 10. Nov 2015 16:49 Titel: Max Cohen Verfasst am: 10. Nov 2015 16:49 Titel: |
 |
|
Hallo jh8979, soll denn die allgemeine Lösung gelöst werden oder ist es richtig das man direkt 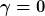 setzen kann? setzen kann?
Falls ich direkt 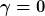 setzen darf erhalte ich für die homogene Lösung setzen darf erhalte ich für die homogene Lösung
=c_1e^{i\omega_0t}+c_2e^{-i\omega_0t})
Nun muss ich noch die partikuläre Lösung finden. Vorab aber erstmal bevor ich versuche diese Lösung zu finden ist der Ansatz soweit korrekt oder übersehe ich hier etwas?
Zuletzt bearbeitet von Max Cohen am 10. Nov 2015 17:26, insgesamt einmal bearbeitet |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 10. Nov 2015 16:53 Titel: jh8979 Verfasst am: 10. Nov 2015 16:53 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | Hallo jh8979, soll denn die allgemeine Lösung gelöst werden oder ist es richtig das man direkt 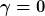 setzen kann? setzen kann?
|
Woher soll ich wissen, was Deine Aufgabe ist?  |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 10. Nov 2015 16:58 Titel: Max Cohen Verfasst am: 10. Nov 2015 16:58 Titel: |
 |
|
|
Wie meinst du das? Ich habe doch die Fragestellung in meinen ersten Post geschrieben. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 10. Nov 2015 17:00 Titel: jh8979 Verfasst am: 10. Nov 2015 17:00 Titel: |
 |
|
|
Dann weiss ich nicht, wieso Du mich fragst: Da steht dann doch, ob Du den Fall gamma=0 betrachten sollst, oder nicht ... |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 10. Nov 2015 17:25 Titel: Max Cohen Verfasst am: 10. Nov 2015 17:25 Titel: |
 |
|
Ehrlich gesagt bin ich mir ziemlich unsicher was es genau zu zeigen gibt.
Wenn ich mich nicht verrechnet habe erhalte ich für die partikuläre Lösung =k_1e^{i\omega t}+k_2e^{-i\omega t})
Das muss ich nun in die ursprüngliche DGL einsetzen. Wenn ich alles richtig gemacht habe erhalte ich:
)
Kannst du mir nicht sagen was ich hier machen soll?
Zuletzt bearbeitet von Max Cohen am 11. Nov 2015 14:08, insgesamt 3-mal bearbeitet |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Nov 2015 13:30 Titel: Max Cohen Verfasst am: 11. Nov 2015 13:30 Titel: |
 |
|
|
Kann mir noch jemand helfen? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Nov 2015 14:43 Titel: jh8979 Verfasst am: 11. Nov 2015 14:43 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: |
Wenn ich mich nicht verrechnet habe erhalte ich für die partikuläre Lösung =k_1e^{i\omega t}+k_2e^{-i\omega t})
|
i.A. ist das keine partikuläre Lösung, sondern nur für bestimmte Werte von k1 und k2.
Ansonsten geht das Lösen wie immer: Allgemeine Lösung der homogenen DGL bestimmten, plus spezielle Lösung der inhomogenen. |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Nov 2015 14:56 Titel: Max Cohen Verfasst am: 11. Nov 2015 14:56 Titel: |
 |
|
Ja genau, die Werte für 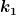 und und 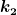 müsste ich nun mittels eines Koeffizientenvergleichs bestimmen. Ich habe p(t) in die DGL eingesetzt und bin auf müsste ich nun mittels eines Koeffizientenvergleichs bestimmen. Ich habe p(t) in die DGL eingesetzt und bin auf
)
gekommen. Nun müsste ich hier wohl einen Koeffizientenvergleich durchführen um 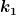 und und 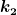 zu bestimmen. Die allgemeine Lösung wäre dann zu bestimmen. Die allgemeine Lösung wäre dann =h(t)+p(t))
Der Koeffizientenvergleich scheint hier aber alles andere als einfach zu sein um die Lösung zu erhalten ...
Ist das denn der richtige Gedanke so das ich mich daran setzen kann? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Nov 2015 15:23 Titel: jh8979 Verfasst am: 11. Nov 2015 15:23 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: |
Der Koeffizientenvergleich scheint hier aber alles andere als einfach zu sein um die Lösung zu erhalten ... |
Dass Das täuscht, wusste Herr E. schon vor 267 Jahren ...  |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Nov 2015 16:17 Titel: Max Cohen Verfasst am: 11. Nov 2015 16:17 Titel: |
 |
|
Ja ich habe es jetzt soweit hinbekommen.
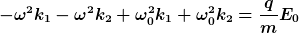
Für den Sinus-Term erhalte ich (Lässt man i dabei stehen?)
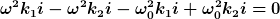
Jetzt habe ich zwei Gleichungen mit 2 unbekannten.
Für 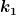 erhalte ich: erhalte ich: }{\omega^2+\omega_0^2})
Ich erhalte durch die zweite Gleichung für }{\omega_0^2-\omega^2})
Das kann ich nun in die erste Gleichung einsetzen. Wenn ich mich nicht verrechnet habe erhalte ich für k_1 folgendes:
(1-\frac{\omega^2-\omega_0^2}{\omega^2+\omega_0^2})})
Damit kann ich nun 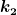 bestimmen. Scheint dir das richtig zu sein? bestimmen. Scheint dir das richtig zu sein?
Wenn ich 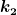 habe wie geht es dann weiter? habe wie geht es dann weiter? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Nov 2015 16:54 Titel: jh8979 Verfasst am: 11. Nov 2015 16:54 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | Scheint dir das richtig zu sein?
|
Keine Ahnung. Rechne k2 aus. Dann setz beides ein und guck ob es eine Lösung der DGL ist. Es gibt wenige Dinge, die leichter sind, als zu gucken, ob die gefundene Lösung für eine DGL richtig ist. |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Nov 2015 18:16 Titel: Max Cohen Verfasst am: 11. Nov 2015 18:16 Titel: |
 |
|
|
Wenn es eine Lösung ist wie rechne ich dann weiter oder war es das schon? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Nov 2015 20:52 Titel: jh8979 Verfasst am: 11. Nov 2015 20:52 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | | Wenn es eine Lösung ist wie rechne ich dann weiter oder war es das schon? |
Was ist denn die Aufgabe? |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Nov 2015 20:58 Titel: Max Cohen Verfasst am: 11. Nov 2015 20:58 Titel: |
 |
|
Ja ich soll zeigen das der harmonische Oszillator im stationären Zustand keine Energie hinzugewinnt. Ich meine mit der Lösung der DGL kann es doch nicht getan sein. Die habe ich nämlich. Ich sehe nämlich nicht warum der Oszillator keine Energie hinzugewinnen könnte.
Für die partikuläre Lösung erhalte ich zumindest einen zeitunabhängigen Ausdruck. Das heißt doch soviel das mit der Zeit sich die Energie nicht ändert.
In der homogenen Lösung taucht allerdings eine Zeitabhängigkeit auf.  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Nov 2015 21:02 Titel: jh8979 Verfasst am: 11. Nov 2015 21:02 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: |
Für die partikuläre Lösung erhalte ich zumindest einen zeitunabhängigen Ausdruck. |
Dann hast Du Dich offensichtlich verrechnet. Setz die Lösung doch einfach mal ein... |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Nov 2015 21:27 Titel: Max Cohen Verfasst am: 11. Nov 2015 21:27 Titel: |
 |
|
Ja, passt offensichtlich nicht. Langsam dreh ich durch.
Ich habe jetzt die Gleichungen:
})
(\omega_0^2-\omega^2)=0)
Aus der zweiten folgt doch das 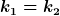 gilt. Damit ist dann gilt. Damit ist dann })
Wenn ich das in meine partikuläre Lösung einsetze =k_1e^{i\omega t}+k_2e^{-i\omega t})
=k_1e^{i\omega t}+k_1e^{-i\omega t})
Das ist meine partikuläre Lösung. Demnach erhalte ich die Lösung =c_1e^{i\omega_0 t}+c_2e^{-i\omega_0 t}+k_1e^{i\omega t}+k_1e^{-i\omega t})
Wenn ich es einsetze erhalte ich nicht Null.  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Nov 2015 21:30 Titel: jh8979 Verfasst am: 11. Nov 2015 21:30 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: |
Aus der zweiten folgt doch das 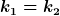 gilt. Damit ist dann gilt. Damit ist dann })
Wenn ich das in meine partikuläre Lösung einsetze =k_1e^{i\omega t}+k_2e^{-i\omega t})
=k_1e^{i\omega t}+k_1e^{-i\omega t})
|
vllt solltest Du das noch etwas vereinfachen, dann sieht man auch leichter, dass es wirklich eine Lösung ist.
| Zitat: |
Das ist meine partikuläre Lösung. Demnach erhalte ich die Lösung =c_1e^{i\omega_0 t}+c_2e^{-i\omega_0 t}+k_1e^{i\omega t}+k_1e^{-i\omega t})
Wenn ich es einsetze erhalte ich nicht Null.  |
Schonmal gut, Null soll ja auch nicht rauskommen... |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Nov 2015 21:43 Titel: Max Cohen Verfasst am: 11. Nov 2015 21:43 Titel: |
 |
|
Ok, die partikuläre Lösung kann ich noch umschreiben mit =2k_1\cos(\omega t))
Wenn ich das in die DGL einsetze erhalte ich:
1=1 somit müsste es doch eine Lösung sein!!! 
Ist damit die Aufgabe erledigt? |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Nov 2015 22:40 Titel: Max Cohen Verfasst am: 11. Nov 2015 22:40 Titel: |
 |
|
|
Ist damit nun die Aufgabe erledigt oder gibt es noch etwas zu zeigen? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Nov 2015 22:47 Titel: jh8979 Verfasst am: 11. Nov 2015 22:47 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | Max Cohen hat Folgendes geschrieben: | | Wenn es eine Lösung ist wie rechne ich dann weiter oder war es das schon? |
Was ist denn die Aufgabe? |
|
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Nov 2015 22:55 Titel: Max Cohen Verfasst am: 11. Nov 2015 22:55 Titel: |
 |
|
|
Ich soll zeigen das der harmonische Oszillator im stationären Zustand keine Energie hinzugewinnt. Also das heißt soviel wie wenn der Oszillator eingeschwungen ist das dieser keine Energie hinzugewinnt. Ich weiß ehrlich gesagt nicht woran ich das nun erkennen soll. Deshalb auch das große Rätselraten meinerseits. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Nov 2015 23:02 Titel: jh8979 Verfasst am: 11. Nov 2015 23:02 Titel: |
 |
|
Mal abgesehen davon, dass es ohne Dämpfung keine Einschwingphase gibt (siehe Lösung der Bewegungsgleichung):
Wie wäre es denn damit die Energie auszurechnen, um zu zeigen, dass nichts dazukommt? Ist jetzt irgendwie kein so grosses Rätsel, wenn man zeigen soll, dass die Energie nicht zunimmt... |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Nov 2015 23:09 Titel: Max Cohen Verfasst am: 11. Nov 2015 23:09 Titel: |
 |
|
Die Gesamtenergie ist 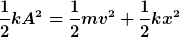
Wie zeige ich das nun damit? Ich muss leider gleich gehen und ich muss die Aufgabe noch fertig bekommen. Nun die Lösung der Bewegungsleichung für  einsetzen und dann? einsetzen und dann? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 11. Nov 2015 23:14 Titel: jh8979 Verfasst am: 11. Nov 2015 23:14 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | Die Gesamtenergie ist 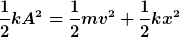
|
Woher weist Du das denn?
| Zitat: |
Wie zeige ich das nun damit? Ich muss leider gleich gehen und ich muss die Aufgabe noch fertig bekommen. Nun die Lösung der Bewegungsleichung für  einsetzen und dann? einsetzen und dann? |
und dann? ... mmhm... schwer zu sagen ...
PS: Sorry, ich hasse dieses kleinteilige Nachfragen nach jedem kleinsten Schritt. Erstens muss man mal lernen selbstständig was zu rechnen und zweitens ist das nun wirklich nicht so schwer gerade... |
|
 |
Max Cohen

Anmeldungsdatum: 13.04.2014
Beiträge: 280
|
 Max Cohen Verfasst am: 11. Nov 2015 23:20 Titel: Max Cohen Verfasst am: 11. Nov 2015 23:20 Titel: |
 |
|
Wenn mir mal ordentlich gesagt würde was zu tun ist und nicht nur gewisse Stichwörter genannt werden dann würde ich mich auch da ran setzen. Die DGL habe ich gelöst und das offensichtlich umsonst wenn sich das Problem auf die Energieerhaltung beschränkt.
Jetzt ist es sowieso zu spät da ich gehen muss.
Danke trotzdem. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 12. Nov 2015 00:05 Titel: jh8979 Verfasst am: 12. Nov 2015 00:05 Titel: |
 |
|
| Max Cohen hat Folgendes geschrieben: | wenn sich das Problem auf die Energieerhaltung beschränkt.
|
Die ist doch genau zu zeigen... einfach sagen "ist erhalten" reicht da offensichtlich nicht aus.
Ausserdem ist das Lösen der Bewegungsgleichung einer erzwungenen Schwingung nichts, wofür man 4 Tage brauchen muss. Mal ganz abgesehen davon, dass das Standardmaterial ist, welches man überall finden kann.
Zuletzt bearbeitet von jh8979 am 12. Nov 2015 00:09, insgesamt einmal bearbeitet |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 12. Nov 2015 00:07 Titel: jh8979 Verfasst am: 12. Nov 2015 00:07 Titel: |
 |
|
|
PS: Im übrigen: Den ursprünglichen Post zu löschen ist mehr als nur schlechte Praxis. Glaubst Du ernsthaft ich mach mir jetzt nochmal die Mühe Dir zu antworten? |
|
 |
|




















