| Autor |
Nachricht |
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 303
|
 vtxt1103 Verfasst am: 27. Nov 2021 16:46 Titel: Zweidimensionaler harmonischer Oszillator vtxt1103 Verfasst am: 27. Nov 2021 16:46 Titel: Zweidimensionaler harmonischer Oszillator |
 |
|
Meine Frage:
Hallo Leute, im Anhang findet ihr eine Aufgabe zum harmonischen Oszilator in 2 dimensionen mit dem ich nicht weiter komme. Ich bedanke mich schonmal für eure Hilfe im Voraus
Meine Ideen:
Ausgehen sollen wir von der newtonischen Bewegungsgleichung
| Beschreibung: |
|

Download |
| Dateiname: |
HO.PNG |
| Dateigröße: |
161.11 KB |
| Heruntergeladen: |
157 mal |
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 28. Nov 2021 09:29 Titel: Myon Verfasst am: 28. Nov 2021 09:29 Titel: |
 |
|
Die Bewegungen in x- und y-Richtung sind ja unabhängig voneinander. Wie sieht denn die allgemeine Lösung aus für einen eindimensionalen harmonischen Oszillator? Was folgt aus den gegebenen Anfangsbedingungen für die Amplituden und Phasenverschiebungswinkel der allgemeinen Lösung für die x- und y-Bewegung?
Zu b) Was folgt aus dem Radius R für die Amplituden der beiden Oszillatoren? Was kann man sonst über die notwendigen Anfangsbedingungen noch sagen? Offensichtlich muss ja jeweils ein Oszillator beim Nulldurchgang sein, wenn der andere die maximale Amplitude hat, damit die Trajektorie kreisförmig wird. Verwende für die notwendigen Bedingungen auch die Energie eines Oszillators für den Zusammenhang zwischen Amplitude und Geschwindigkeit beim Nulldurchgang.
Zu c) Damit nach endlicher Zeit t die Trajektorie wieder einen gleichen Punkt erreicht, muss dieses t ein ganzzahliges Vielfaches der beiden Perioden sein, d.h. es muss gelten
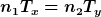
für natürliche n1, n2. Was bedeuetet das für das Verhältnis 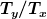 bzw. das Verhältnis bzw. das Verhältnis 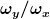 ? ?
|
|
 |
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 303
|
 vtxt1103 Verfasst am: 28. Nov 2021 20:34 Titel: vtxt1103 Verfasst am: 28. Nov 2021 20:34 Titel: |
 |
|
|
Müsste dann bei der a nicht eine kreisförmige und eine elipsenförmige bewegung rauskommen ?
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 28. Nov 2021 21:10 Titel: Myon Verfasst am: 28. Nov 2021 21:10 Titel: |
 |
|
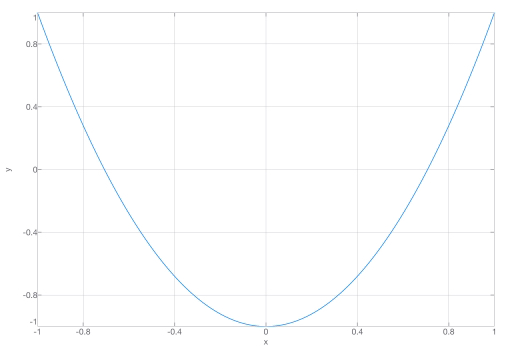
Nein, es ergibt sich weder ein Kreis (es gilt ja immer x(t)=y(t), somit ...?) noch eine Ellipse. Für eine nichtentartete Ellipse müssten die Amplituden unterschiedlich sein. Du kannst ja überlegen, wo die Punkte (x,y) liegen bei einer halben Periode Tx, bei einer ganzen Periode Tx usw. Es sollte sich etwas ergeben wie im untenstehenden Plot.
PS: Man sieht es vielleicht nicht so genau auf dem Plot, aber die Trajektorie geht nicht durch (0,0), sondern durch (0,-1).
| Beschreibung: |
|
| Dateigröße: |
40.06 KB |
| Angeschaut: |
980 mal |
|
|
|
 |
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 303
|
 vtxt1103 Verfasst am: 28. Nov 2021 21:44 Titel: vtxt1103 Verfasst am: 28. Nov 2021 21:44 Titel: |
 |
|
|
Ach okay man hat eine gerade und eine nach rechts geöffnete Parabel
|
|
 |
vtxt1103
Anmeldungsdatum: 14.11.2021
Beiträge: 303
|
 vtxt1103 Verfasst am: 28. Nov 2021 22:32 Titel: vtxt1103 Verfasst am: 28. Nov 2021 22:32 Titel: |
 |
|
Zu b) Was folgt aus dem Radius R für die Amplituden der beiden Oszillatoren? Was kann man sonst über die notwendigen Anfangsbedingungen noch sagen? Offensichtlich muss ja jeweils ein Oszillator beim Nulldurchgang sein, wenn der andere die maximale Amplitude hat, damit die Trajektorie kreisförmig wird. Verwende für die notwendigen Bedingungen auch die Energie eines Oszillators für den Zusammenhang zwischen Amplitude und Geschwindigkeit beim Nulldurchgang.
für die beiden Oszilatoren kommen dann ja nur sinus und cosinus in betracht und der Radius muss konstant sein, somit würde sich ergeben
x,y(t) R*cos(ω*t)
R*sin(ω*t)
Richtig ?
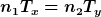
für natürliche n1, n2. Was bedeuetet das für das Verhältnis 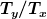 bzw. das Verhältnis bzw. das Verhältnis 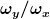 ?[/quote] ?[/quote]
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 29. Nov 2021 09:08 Titel: Myon Verfasst am: 29. Nov 2021 09:08 Titel: |
 |
|
| vtxt1103 hat Folgendes geschrieben: | | Ach okay man hat eine gerade und eine nach rechts geöffnete Parabel |
Für 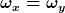 ergibt sich eine Gerade von (-R,R) bis (R,R). Für ergibt sich eine Gerade von (-R,R) bis (R,R). Für 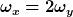 sieht die Trajektorie ähnlich wie eine Parabel aus, es ist aber keine. Vgl. den Plot für R=1, hier müsste gelten sieht die Trajektorie ähnlich wie eine Parabel aus, es ist aber keine. Vgl. den Plot für R=1, hier müsste gelten 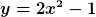 , was nicht der Fall ist. , was nicht der Fall ist.
| Zitat: | x,y(t) R*cos(ω*t)
R*sin(ω*t)
Richtig ? |
Ja, für
\\y(t)\end{pmatrix}=\begin{pmatrix}R\cos(\omega t)\\R\sin(\omega t)\end{pmatrix})
ergibt sich ein Kreis. Hinreichende Anfangsbedingungen wären also
\\y(0)\end{pmatrix}=\begin{pmatrix}R\\0\end{pmatrix},\quad \begin{pmatrix}\dot{x}(0)\\\dot{y}(0)\end{pmatrix}=\begin{pmatrix}0\\\omega R\end{pmatrix})
Notwendig sind die Bedingungen nicht, denn es könnte noch eine Phasenverschiebung hinzukommen. Notwendig und hinreichend ist also, wenn für ein ) gilt gilt
\\y(0)\end{pmatrix}=\begin{pmatrix}R\cos\theta\\R\sin\theta\end{pmatrix},\quad \begin{pmatrix}\dot{x}(0)\\\dot{y}(0)\end{pmatrix}=\begin{pmatrix}-\omega R\sin\theta\\\omega R\cos\theta\end{pmatrix}) . .
|
|
 |
|
















