| Autor |
Nachricht |
clueless_noob
Gast
|
 clueless_noob Verfasst am: 27. Apr 2020 11:48 Titel: Integral über Produkt von Mayer-f-Funktionen clueless_noob Verfasst am: 27. Apr 2020 11:48 Titel: Integral über Produkt von Mayer-f-Funktionen |
 |
|
Meine Frage:
Hallo!
Ich möchte ein Integral über das Produkt zweier Mayer-f-Funktionen für harte Kugeln ausführen:
*f(\vec{r} - \vec{r'}) \, \dd \vec{r'} )
 = -1 ; f(\vec{r}, r\geq\sigma = 0)
Dabei ist 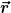 der Verbindungsvektor zwischen zwei Kugeln gleicher Art mit Durchmesser der Verbindungsvektor zwischen zwei Kugeln gleicher Art mit Durchmesser 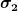 und und 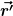 verbindet eine Kugel vom Typ 2 mit einer Kugel anderer Art ( verbindet eine Kugel vom Typ 2 mit einer Kugel anderer Art (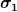 ). ).
Die Integration über die f-Funktion, die nur von 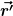 abhängt ist kein Problem. Aber ich weiß nicht, wie ich mit der anderen Funktion, welche die Subtraktion enthält, umgehen soll. abhängt ist kein Problem. Aber ich weiß nicht, wie ich mit der anderen Funktion, welche die Subtraktion enthält, umgehen soll.
Meine Ideen:
Die Funktion hängt ja eigentlich nur vom Betrag des Verbindungsvektors ab.
Daher wollte ich diesen durch die beiden Vektoren parametrisieren.
Aber ich hab leider noch keinen sinnvollen Ansatz dafür gefunden....
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 27. Apr 2020 12:23 Titel: Steffen Bühler Verfasst am: 27. Apr 2020 12:23 Titel: |
 |
|
Es ist zwar nicht mein Fachgebiet, aber wenn Du Dir die beiden zu multiplizierenden Funktionen skizzierst, siehst Du, dass das Produkt für 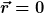 im Bereich im Bereich 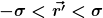 Eins ist, sonst Null. Eins ist, sonst Null.
Wenn Du nun 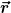 erhöhst, wird dieser Bereich zunächst kleiner, geht auf Null, um dann wieder größer zu werden. So kannst Du das Integral in Abhängigkeit von erhöhst, wird dieser Bereich zunächst kleiner, geht auf Null, um dann wieder größer zu werden. So kannst Du das Integral in Abhängigkeit von 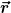 angeben. angeben.
Viele Grüße
Steffen
|
|
 |
clueless_noob
Gast
|
 clueless_noob Verfasst am: 27. Apr 2020 16:29 Titel: clueless_noob Verfasst am: 27. Apr 2020 16:29 Titel: |
 |
|
| Steffen Bühler hat Folgendes geschrieben: | Es ist zwar nicht mein Fachgebiet, aber wenn Du Dir die beiden zu multiplizierenden Funktionen skizzierst, siehst Du, dass das Produkt für 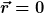 im Bereich im Bereich 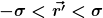 Eins ist, sonst Null. Eins ist, sonst Null.
Wenn Du nun 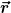 erhöhst, wird dieser Bereich zunächst kleiner, geht auf Null, um dann wieder größer zu werden. So kannst Du das Integral in Abhängigkeit von erhöhst, wird dieser Bereich zunächst kleiner, geht auf Null, um dann wieder größer zu werden. So kannst Du das Integral in Abhängigkeit von 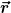 angeben. angeben.
Viele Grüße
Steffen |
Ich steh auf dem Schlauch oder ich bin zu blöd, jedenfalls verstehe ich leider nicht so ganz wie du das meins.
Die Funktion hängt ja vom Betrag des Verbindungsvektors der Raumpunkte ab. Aber da es sich um Vektoren handelt spielt die Orientierung ja auch eine Rolle, will sagen:
Wenn ich einfach nur einen bestimmten Betrag für r annehme, ist die Länge des Verbindungsvektors ja trotzdem noch von der Orientierung von r abhängig.
Ich hatte jetzt noch eine andere Idee:
Wenn ich jetzt den Verbindungsvektor der beiden gleichartigen Kugeln entlang der z-Achse annehme, dann entspricht der Winkel zwischen 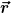 und und 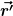 ja dem Azimutwinkel in Kugelkoordinaten. ja dem Azimutwinkel in Kugelkoordinaten.
|
|
 |
clueless_noob
Gast
|
 clueless_noob Verfasst am: 27. Apr 2020 16:32 Titel: clueless_noob Verfasst am: 27. Apr 2020 16:32 Titel: |
 |
|
Ich hatte jetzt noch eine andere Idee:
Wenn ich jetzt den Verbindungsvektor der beiden gleichartigen Kugeln entlang der z-Achse annehme, dann entspricht der Winkel zwischen 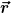 und und 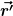 ja dem Azimutwinkel in Kugelkoordinaten.[/quote] ja dem Azimutwinkel in Kugelkoordinaten.[/quote]
OK, das bringt mich wohl leider auch nicht weiter....
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 27. Apr 2020 17:04 Titel: Steffen Bühler Verfasst am: 27. Apr 2020 17:04 Titel: |
 |
|
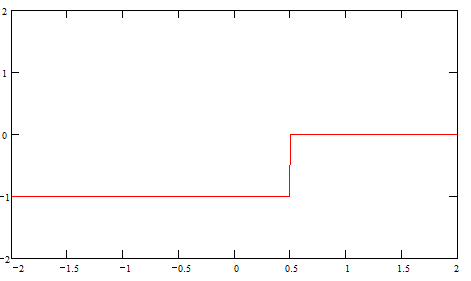
Was ich meine, siehst Du unten in den zwei Diagrammen. Das obere zeigt die Funktion ) , das untere die Funktion , das untere die Funktion ) . Das ganze ist jeweils über der . Das ganze ist jeweils über der 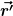 -Achse aufgetragen, denn darüber wird ja integriert. Dann ist -Achse aufgetragen, denn darüber wird ja integriert. Dann ist 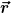 eine Konstante, die ich für das Beispiel auf Null gesetzt habe. Und eine Konstante, die ich für das Beispiel auf Null gesetzt habe. Und 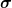 ist fest auf 0,5 gesetzt. ist fest auf 0,5 gesetzt.
Dann ergibt die Multiplikation beider Funktionen eine Produktfunktion, die von -0,5 bis +0,5 den Wert 1 hat und ansonsten Null ist. Das Integral (die Fläche) hat somit ebenfalls den Wert 1.
Das ist nun der Integralwert für 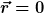 , andere Werte kann man entsprechend berechnen. , andere Werte kann man entsprechend berechnen.
Ich bin zwar nach wie vor nicht sicher, ob dieser rein mathematische, von keinerlei weiterer Kenntnis getrübter Ansatz Dich weiterbringt, aber wer weiß...
| Beschreibung: |
|
| Dateigröße: |
2.12 KB |
| Angeschaut: |
1054 mal |
|
| Beschreibung: |
|
| Dateigröße: |
2.09 KB |
| Angeschaut: |
1054 mal |
|
|
|
 |
clueless_noob
Gast
|
 clueless_noob Verfasst am: 27. Apr 2020 17:30 Titel: clueless_noob Verfasst am: 27. Apr 2020 17:30 Titel: |
 |
|
Erstmal vielen vielen Dank, dass du dir so viel Mühe machst.
Was ich nicht verstehe ist folgendes:
Wenn 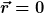 dann macht das für mich alles Sinn. dann macht das für mich alles Sinn.
Aber 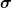 ist nur ein Skalar, was die Bedingung für den Betrag der Vektoren gibt. ist nur ein Skalar, was die Bedingung für den Betrag der Vektoren gibt.
Wenn 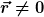 spielt die Orientierung der beiden Vektoren zueinander auch eine Rolle. spielt die Orientierung der beiden Vektoren zueinander auch eine Rolle.
Ich gehe mal vom Betrag aus:
)^{\frac{1}{2}})
Ich weiß, dass der Betrag kleiner 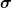 sein muss. Ich habe durch das Produkt mit f(r') auch eine Bedingung für r'. Aber ich kenne den eingeschlossenen Winkel sein muss. Ich habe durch das Produkt mit f(r') auch eine Bedingung für r'. Aber ich kenne den eingeschlossenen Winkel 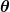 nicht und habe keine dafür gegeben. nicht und habe keine dafür gegeben.
Wenn 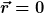 ist das ja kein Problem. ist das ja kein Problem.
|
|
 |
clueless_noob
Gast
|
 clueless_noob Verfasst am: 27. Apr 2020 17:48 Titel: clueless_noob Verfasst am: 27. Apr 2020 17:48 Titel: |
 |
|
Mir ist noch was aufgefallen:
Wieso ist die Mayerfunktion f(r'-r) gleich -1 für 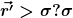 es gilt doch folgendes: es gilt doch folgendes:
 = -1, f(\vec{r'}, r'\geq \sigma) = 0 )
So sollte sich die Funktion doch verhalten wenn 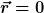
|
|
 |
clueless_noob
Gast
|
 clueless_noob Verfasst am: 27. Apr 2020 18:11 Titel: clueless_noob Verfasst am: 27. Apr 2020 18:11 Titel: |
 |
|
| clueless_noob hat Folgendes geschrieben: | Mir ist noch was aufgefallen:
Wieso ist die Mayerfunktion f(r'-r) gleich -1 für 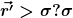 es gilt doch folgendes: es gilt doch folgendes:
 = -1, f(\vec{r'}, r'\geq \sigma) = 0 )
So sollte sich die Funktion doch verhalten wenn 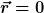 |
Ok vergiss das, ich hab den einen Abschnitt von dir nur nicht richtig gelesen
|
|
 |
Gast002
Gast
|
 Gast002 Verfasst am: 27. Apr 2020 21:43 Titel: Gast002 Verfasst am: 27. Apr 2020 21:43 Titel: |
 |
|
Hallo,
Spezialist auf dem Gebiet bin ich auch nicht. Aber ich denke, der Vektorcharakter von 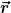 muß eine Rolle spielen. muß eine Rolle spielen.
Mit der Schreibweise, wie ) definiert wurde, komme ich nicht richtig klar. Daher hier eine andere Schreibweise, so wie ich es verstanden habe: definiert wurde, komme ich nicht richtig klar. Daher hier eine andere Schreibweise, so wie ich es verstanden habe:
 = \Big\{ {{-1 \quad wenn \quad r < \sigma} \atop { 0 \quad wenn \quad r \geq \sigma}})
Ist das richtig so?
Wenn es richtig ist, schlage ich folgenden Weg zur Berechnung des Integrals vor:
- Das Koordinatensystem wird so gelegt, daß der bei der Integration konstante Vektor 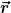 in Richtung der z-Achse zeigt. Dann ist das ganze Problem rotationssymmetrisch zur z-Achse. in Richtung der z-Achse zeigt. Dann ist das ganze Problem rotationssymmetrisch zur z-Achse.
- Die Integration wird in Kugelkoordinaten (für den Vektor 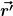 ) ausgeführt ) ausgeführt
- Für die Berechnung der Funktion ) braucht man den Betrag braucht man den Betrag 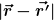 . Der kann über den Kosinussatz aus den Beträgen beider Vektoren und dem Winkel zwischen ihnen bestimmt werden. . Der kann über den Kosinussatz aus den Beträgen beider Vektoren und dem Winkel zwischen ihnen bestimmt werden.
Damit könnte die Berechnung des Integrals machbar sein.
|
|
 |
clueless_noob
Gast
|
 clueless_noob Verfasst am: 27. Apr 2020 22:30 Titel: clueless_noob Verfasst am: 27. Apr 2020 22:30 Titel: |
 |
|
Ja die Definition von f(r) ist richtig so, wie du sie geschrieben hast. Ich wusste nur nicht, wie ich im latex die geschweifte Klammer so machen kann 
Die Idee hatte ich auch, aber ich hab damit keinen Erfolg gehabt. Für heute mach ich schluss und versuch es dann morgen wieder.
|
|
 |
Gast002
Gast
|
 Gast002 Verfasst am: 28. Apr 2020 20:10 Titel: Gast002 Verfasst am: 28. Apr 2020 20:10 Titel: |
 |
|
Hallo,
falls es Dich interessiert, hier ist der Latexausdruck für die Funktionsdefinition:
f(\vec{r}) = \Big\{ {{-1 \quad wenn \quad r < \sigma} \atop { 0 \quad wenn \quad r \geq \sigma}}
Schreib, wo Du bei der Lösung des Integrals hängenbleibst.
|
|
 |
|


















