| Autor |
Nachricht |
physikfan
Anmeldungsdatum: 15.06.2010
Beiträge: 21
|
 physikfan Verfasst am: 02. Nov 2011 16:25 Titel: Wellenpaket, Superposition Summe => Integral ? physikfan Verfasst am: 02. Nov 2011 16:25 Titel: Wellenpaket, Superposition Summe => Integral ? |
 |
|
Man möchte ja Wellen nach dem Superpositionsprinzip aufsummieren, um ein Wellenpaket zu erhalten. Dabei verstehe ich nicht, wieso man da von der Summe zum Integral übergehen kann. Integral und Summe sind doch nicht genau das gleiche.
Das sieht man doch alleine schon daran, dass sich durch Integration die Einheit verändert..
Wieso kann man dann bei der Superposition ein Integral bilden? Liegt das daran, dass jedes "infinitesimales Teilintervall" die gleiche Länge hat und somit sich quasi Integral und Summe nur um ein Vielfaches unterscheiden?
Weiterhin verstehe ich nicht wieso man über k integriert. Hängt das damit zusammen, dass man alle möglichen Zustände, die mit dem Impuls zusammenhängen, der ja mit k verknüpft ist, erfassen möchte? Aber wieso integriert man nicht z.B. über die Kreisfrequenz. |
|
 |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 02. Nov 2011 17:39 Titel: Re: Wellenpaket, Superposition Summe => Integral ? Chillosaurus Verfasst am: 02. Nov 2011 17:39 Titel: Re: Wellenpaket, Superposition Summe => Integral ? |
 |
|
| physikfan hat Folgendes geschrieben: | | Man möchte ja Wellen nach dem Superpositionsprinzip aufsummieren, um ein Wellenpaket zu erhalten. Dabei verstehe ich nicht, wieso man da von der Summe zum Integral übergehen kann.[...] |
Fügt man anstelle des Summenzeichens Delta-Distributionen ein und integriert, sind beide Darstellungen exakt äquivalent. |
|
 |
DivGradPot
Anmeldungsdatum: 07.07.2019
Beiträge: 45
|
 DivGradPot Verfasst am: 10. Aug 2019 11:35 Titel: DivGradPot Verfasst am: 10. Aug 2019 11:35 Titel: |
 |
|
|
Haargenau die gleiche Frage beschäftigt mich im Moment, auch hat jemand dazu eine Antwort mittlerweile? Mich stört vor allem das sich die Einehit beim Integral erhöht. |
|
 |
Chillosaurus
Anmeldungsdatum: 07.08.2010
Beiträge: 2440
|
 Chillosaurus Verfasst am: 10. Aug 2019 11:46 Titel: Chillosaurus Verfasst am: 10. Aug 2019 11:46 Titel: |
 |
|
|
Schreibe bitte ein Beispiel detailliert hin, ansonsten kann niemand raten, was du genau meinst... |
|
 |
Nescio

Anmeldungsdatum: 05.12.2015
Beiträge: 279
|
 Nescio Verfasst am: 10. Aug 2019 13:36 Titel: Re: Wellenpaket, Superposition Summe => Integral ? Nescio Verfasst am: 10. Aug 2019 13:36 Titel: Re: Wellenpaket, Superposition Summe => Integral ? |
 |
|
Ein Integral ist eine Summe, bei der man den Grenzwert gegen unendlich viele infinitesimal kleine Summanden ausgeführt hat. Zum Beispiel kann man die Fläche unter ) annähern als Summe von Rechtecken der Höhe annähern als Summe von Rechtecken der Höhe ) und Breite und Breite 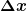 (siehe Riemannsches Integral). Wenn ich die Breite der Intervalle unendlich klein mache erhalte ich (siehe Riemannsches Integral). Wenn ich die Breite der Intervalle unendlich klein mache erhalte ich
 dx =\lim\limits_{\Delta x \rightarrow 0}\sum_{i=a /\Delta x}^{b/\Delta x} f(i\Delta x)\Delta x)
Die Einheit verändert sich durch die Multiplikation mit dem 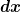 bzw. bzw. 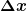 . .
Historisch leitet sich sogar das Integralsymbol daraus ab
| Zitat: | | Die symbolische Schreibweise von Integralen geht auf den Miterstbeschreiber der Differential- und Integralrechnung, Gottfried Wilhelm Leibniz, zurück. Das Integralzeichen ∫ ist aus dem Buchstaben langes s (ſ) für lateinisch summa abgeleitet. Die multiplikativ zu lesende Notation f(x) dx deutet an, wie sich das Integral – dem Riemann-Integral folgend – aus Streifen der Höhe f(x) und der infinitesimalen Breite dx zusammensetzt. |
|
|
 |
DivGradPot
Anmeldungsdatum: 07.07.2019
Beiträge: 45
|
 DivGradPot Verfasst am: 10. Aug 2019 18:37 Titel: DivGradPot Verfasst am: 10. Aug 2019 18:37 Titel: |
 |
|
Hellooo,
Schön das sich doch noch wer meldet trotz der langen zeit des threads.
Yo yo Das ist der Übergang von einer Summe zum Integral, das ist mir bekannt und tatsächlich versteh ich das sogar (glaub ich): Dann bitte ich dich aber mal nen Blick auf folgendes zu werfen, mal sehen ob das damit auch geht, ich sehe es jedenfalls nicht das das funktioniert mit dieser Erklärung...
Man hat also eine Lösung der SGL, sagen wir sie heißt  )
Eine Lösung wäre also durch den Ansatz:  = \phi(k) e^{-i(kx-wt)} )
Dann sagt man das auch die Superposition der Lösungen, also verschiedenen Amplituden auch eine Lösung sind und schreibt diese als Summe:
 = \sum\limits_{k=1}^{\infty} \phi(k) e^{-i(kx-wt)} )
Das Phi von k soll dabei die komplexe Amplitude darstellen und dann geht man zur Integraldarstellung weil k kontinuirlich ist und wie du ja schon geschrieben hast kann man ja Summen so dann als Integral schreiben:
 = \int_{-\infty}^{\infty} \! \phi(k) e^{-i(kx-wt)} \, \dd k )
So und hier fällt jetzt auf was schon der Fragesteller angemerkt hat genauso wie auch mein Problem ist: Da istplötzlich dieses dk was einfach so auftaucht und offenbar die Wellenfkt. Psi einfach mal um eine k-te Einheit erhöht... Wie kann das sein das das die gleiche Wellenfkt sein soll??? Das ist eigentlich nicht möglich. Ich hoffe man sieht jetzt mal mein Problem und das des Fragestellers, das wird nämlich irgendwie nie erklärt und hab auch sonst nichts dazu gefunden.
Beste Grüße Jan |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 10. Aug 2019 19:20 Titel: jh8979 Verfasst am: 10. Aug 2019 19:20 Titel: |
 |
|
| DivGradPot hat Folgendes geschrieben: |
Dann sagt man das auch die Superposition der Lösungen, also verschiedenen Amplituden auch eine Lösung sind und schreibt diese als Summe:
 = \sum\limits_{k=1}^{\infty} \phi(k) e^{-i(kx-wt)} )
|
Ich weiss nicht wer "man" ist, aber das hier ist natürlich ein Problem, da k nicht einheitenlos sein kann, wenn es in der Verbingung ikx in der e-Funktion vorkommt....
Man muss es halt ordentlich machen dann klärt sich auch der Rest.
(oder man pfuscht es physikermäßig hin und hofft, dass es am Ende passt, aber dann entstehen Fragen wie Deine  ) ) |
|
 |
Nescio

Anmeldungsdatum: 05.12.2015
Beiträge: 279
|
 Nescio Verfasst am: 10. Aug 2019 20:06 Titel: Nescio Verfasst am: 10. Aug 2019 20:06 Titel: |
 |
|
Die beiden ) in den beiden Gleichungen sind nicht identisch und haben auch nicht die gleiche Einheit. Es ist verwirrend, dass du beide Versionen gleich benannt hast, deshalb werde ich ab jetzt in den beiden Gleichungen sind nicht identisch und haben auch nicht die gleiche Einheit. Es ist verwirrend, dass du beide Versionen gleich benannt hast, deshalb werde ich ab jetzt
 = \sum\limits_{j=1}^{\infty} \phi(k_j) e^{-i(k_jx-w_jt)} )
und
 = \int_{-\infty}^{\infty} \! \phi'(k) e^{-i(kx-wt)} \, \dd k )
verwenden.
Da|^2 dx) dimensionslos sein muss und dimensionslos sein muss und 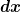 die Einheit die Einheit 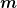 hat, muss hat, muss ) die Einheit die Einheit  haben. Demnach muss haben. Demnach muss ) die Einheit die Einheit  haben. haben.
Dagegen hat ) die Einheit die Einheit  . Außerdem würde man wahrscheinlich eher . Außerdem würde man wahrscheinlich eher  schreiben, da es sich um diskrete Koeffizienten handelt, nicht um eine kontinuierliche Funktion. schreiben, da es sich um diskrete Koeffizienten handelt, nicht um eine kontinuierliche Funktion.
Außerdem ist im allgemeinen  , es seie denn du wählst als , es seie denn du wählst als ) eine Summe von Deltafunktionen. In dem Falle müsstest du die Einheiten der Deltafunktion mit berücksichtigen bei der Einheitenrechnung. eine Summe von Deltafunktionen. In dem Falle müsstest du die Einheiten der Deltafunktion mit berücksichtigen bei der Einheitenrechnung.
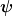 ist eine Wellenfunktion mit diskreter Frequenzverteilung und ist eine Wellenfunktion mit diskreter Frequenzverteilung und 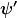 eine Wellenfunktion mit kontinuierlicher Frequenzverteilung. eine Wellenfunktion mit kontinuierlicher Frequenzverteilung.
Das Superpositionsprinzip lässt sich trotzdem für die kontinuierliche Frequenzverteilung anwenden, da man wie oben beschrieben das Integral als Grenzwert einer Summe (von Lösungen der SG) darstellen kann.
Zuletzt bearbeitet von Nescio am 10. Aug 2019 20:59, insgesamt 2-mal bearbeitet |
|
 |
DivGradPot
Anmeldungsdatum: 07.07.2019
Beiträge: 45
|
 DivGradPot Verfasst am: 10. Aug 2019 20:11 Titel: DivGradPot Verfasst am: 10. Aug 2019 20:11 Titel: |
 |
|
Und wie löst sich das Problem jetzt? Das ist doch nicht legitim sowas zu machen oder doch?
Hab ich auch so gesehen als beweis, sehr oft sogar, sonst wird auch manchmal mit der Amplitude was ersetzt durch Substitution und so das dk rein bekommt aber das wird ja dann trotzdem etwas anderes sein, dieses Integral, als wenn ich alle Wellenfkt. aufsummiere. Eigentlich müsste da sowas wie:
 = \int_{-\infty}^{\infty} \! 1 \, \dd (\phi (k) e^{-i(kx-wt)}) )
Wie macht man es denn ordentlich, hat jemand nen Link oder Skriptoder sonst was dazu?
Aber mich würd erstmal interessieren ob das hier überhaupt so stimmt oder ob es doch falsch ist.
Kann man hier eigentlich zitieren oder so aus früheren Beiträgen also Formeln übernehmen mein ich, die muss man immer wieder neu schreiben das ist voll nervig.[/quote] |
|
 |
DivGradPot
Anmeldungsdatum: 07.07.2019
Beiträge: 45
|
 DivGradPot Verfasst am: 10. Aug 2019 20:13 Titel: DivGradPot Verfasst am: 10. Aug 2019 20:13 Titel: |
 |
|
Hey Nescio,
Das hab ich ja nicht so gemacht, den Beweis hab ich nur übernommen und hab ich erschreckend oft im Inet gesehen. aber danke schon mal ich wird mir den gleich mal ansehen und noch fragen stellen wenn ich welche hab.
Danke auf jeden fall dann weiß ich das ich mich da nicht irre |
|
 |
Nescio

Anmeldungsdatum: 05.12.2015
Beiträge: 279
|
 Nescio Verfasst am: 10. Aug 2019 20:24 Titel: Nescio Verfasst am: 10. Aug 2019 20:24 Titel: |
 |
|
| DivGradPot hat Folgendes geschrieben: |
Kann man hier eigentlich zitieren oder so aus früheren Beiträgen also Formeln übernehmen mein ich, die muss man immer wieder neu schreiben das ist voll nervig. |
Im Beitrag oben rechts auf "Zitat" klicken. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 10. Aug 2019 20:43 Titel: jh8979 Verfasst am: 10. Aug 2019 20:43 Titel: |
 |
|
| Nescio hat Folgendes geschrieben: |
 = \sum\limits_{k=1}^{\infty} \phi(k) e^{-i(kx-wt)} )
|
das ist immer noch ein Problem von der Einheit von k ... aber macht was ihr wollt... |
|
 |
Nescio

Anmeldungsdatum: 05.12.2015
Beiträge: 279
|
 Nescio Verfasst am: 10. Aug 2019 20:46 Titel: Nescio Verfasst am: 10. Aug 2019 20:46 Titel: |
 |
|
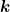 hat die Einheit hat die Einheit  . Ich kann da kein Problem erkennen. . Ich kann da kein Problem erkennen. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 10. Aug 2019 20:53 Titel: jh8979 Verfasst am: 10. Aug 2019 20:53 Titel: |
 |
|
| Nescio hat Folgendes geschrieben: | 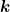 hat die Einheit hat die Einheit  . Ich kann da kein Problem erkennen. . Ich kann da kein Problem erkennen. |
Ich schon, wenn k=1 sein soll.... |
|
 |
Nescio

Anmeldungsdatum: 05.12.2015
Beiträge: 279
|
 Nescio Verfasst am: 10. Aug 2019 20:55 Titel: Nescio Verfasst am: 10. Aug 2019 20:55 Titel: |
 |
|
|
Ah verdammt, das hab ich total übersehen. Jetzt passt es hoffentlich. |
|
 |
DivGradPot
Anmeldungsdatum: 07.07.2019
Beiträge: 45
|
 DivGradPot Verfasst am: 11. Aug 2019 07:39 Titel: DivGradPot Verfasst am: 11. Aug 2019 07:39 Titel: |
 |
|
Hallo ihr beiden,
Ehm das mit dem Zitieren will irgendwie nicht, wenn ich auf Quote klicke dann kommt nur die Umgebung aber ich meinte ob man einfach Formeln kopieren kann oder die Beiträge.
Okaaaay zum eigentlichen Thema bin ich leider raus  was genau hat dich an der Summe gestört jh? Ist die wegen doppelter Nutzung von k falsch gewesen oder was passte dort nicht? was genau hat dich an der Summe gestört jh? Ist die wegen doppelter Nutzung von k falsch gewesen oder was passte dort nicht? |
|
 |
DivGradPot
Anmeldungsdatum: 07.07.2019
Beiträge: 45
|
 DivGradPot Verfasst am: 11. Aug 2019 07:40 Titel: DivGradPot Verfasst am: 11. Aug 2019 07:40 Titel: |
 |
|
Hallo ihr beiden,
Ehm das mit dem Zitieren will irgendwie nicht, wenn ich auf Quote klicke dann kommt nur die Umgebung aber ich meinte ob man einfach Formeln kopieren kann oder die Beiträge.
Okaaaay zum eigentlichen Thema bin ich leider raus  was genau hat dich an der Summe gestört jh? Ist die wegen doppelter Nutzung von k falsch gewesen oder was passte dort nicht? was genau hat dich an der Summe gestört jh? Ist die wegen doppelter Nutzung von k falsch gewesen oder was passte dort nicht? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 11. Aug 2019 09:27 Titel: Re: Wellenpaket, Superposition Summe => Integral ? TomS Verfasst am: 11. Aug 2019 09:27 Titel: Re: Wellenpaket, Superposition Summe => Integral ? |
 |
|
| physikfan hat Folgendes geschrieben: | | Man möchte ja Wellen nach dem Superpositionsprinzip aufsummieren, um ein Wellenpaket zu erhalten. Dabei verstehe ich nicht, wieso man da von der Summe zum Integral übergehen kann. Integral und Summe sind doch nicht genau das gleiche. |
Evtl. ist es einfacher, sich das ursprüngliche Problem anzusehen.
Gegeben ist ein (selbstadjungierter) Differentialoperator D in d/dx mit einer Eigenwertgleichung
\,u_\lambda(x) = 0)
Wenn das Problem auf einem kompakten Intervall

definiert ist, dann hat D ein diskretes Spektrum, d.h. die Eigenfunktionen u sind abzählbar und man findet
 = \sum_\lambda \psi_\lambda \, u_\lambda(x))
Wenn x auf einem nicht-kompakten Raum wie z.B. den reellen Zahlen definiert ist

dann hat D ein kontinuierliches Spektrum, d.h. die verallgemeinerten Eigenfunktionen u sind nicht mehr abzählbar und man findet
 = \int d\lambda \, \psi_\lambda \, u_\lambda(x))
Dazu benötigt man auch keinen Grenzübergang; diese Idee ist zwar physikalisch irgendwie intuitiv, jedoch mathematisch unsauber.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Nescio

Anmeldungsdatum: 05.12.2015
Beiträge: 279
|
 Nescio Verfasst am: 11. Aug 2019 10:43 Titel: Nescio Verfasst am: 11. Aug 2019 10:43 Titel: |
 |
|
| DivGradPot hat Folgendes geschrieben: |
Okaaaay zum eigentlichen Thema bin ich leider raus  was genau hat dich an der Summe gestört jh? Ist die wegen doppelter Nutzung von k falsch gewesen oder was passte dort nicht? was genau hat dich an der Summe gestört jh? Ist die wegen doppelter Nutzung von k falsch gewesen oder was passte dort nicht? |
k ist die Wellenzahl und kein Summationsindex. Das passt auch von der Einheit nicht. Den Summationsindex hattest du komplett vergessen. Das habt ihr auch sicherlich in der Vorlesung nicht so aufgeschrieben, guck das doch mal nach. |
|
 |
DivGradPot
Anmeldungsdatum: 07.07.2019
Beiträge: 45
|
 DivGradPot Verfasst am: 14. Aug 2019 10:57 Titel: DivGradPot Verfasst am: 14. Aug 2019 10:57 Titel: |
 |
|
In der Vorlesung haben wir erst gar nicht die Summe aufgeschrieben sondern das Integral direkt, aber das ist nicht so wichtig, ich wollte das im Detail verstehen und bin auf sowas im Internet gestoßen.
Also warum genau hatte das jetzt nicht gepasst? Ich hab die erste Version nicht mehr im Kopf im Detail, hast du da jetzt einfach die Summe über j laufen lassen anstatt über k? Also dann ja stimmt darauf hab ich auch nicht geachtet, darum ging es mir aber auch gar nicht. |
|
 |
Nescio

Anmeldungsdatum: 05.12.2015
Beiträge: 279
|
 Nescio Verfasst am: 14. Aug 2019 12:00 Titel: Nescio Verfasst am: 14. Aug 2019 12:00 Titel: |
 |
|
| DivGradPot hat Folgendes geschrieben: | | Ich hab die erste Version nicht mehr im Kopf im Detail, hast du da jetzt einfach die Summe über j laufen lassen anstatt über k? |
Die erste Version steht immer noch in deinem Beitrag. Scroll mal nach oben und vergleiche mit der korrigierten Version die ich hingeschrieben habe?
| DivGradPot hat Folgendes geschrieben: |
darum ging es mir aber auch gar nicht. |
Mir auch nicht. Ich bin auf das was du meinst ausführlich in meinen ersten beiden Beiträgen eingegangen. TomS hat eine andere Alternative dazu geliefert. Hast du vielleicht konkrete Fragen dazu? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18067
|
 TomS Verfasst am: 14. Aug 2019 13:57 Titel: TomS Verfasst am: 14. Aug 2019 13:57 Titel: |
 |
|
| Nescio hat Folgendes geschrieben: | | k ist die Wellenzahl und kein Summationsindex. Das passt auch von der Einheit nicht. |
Ok, die Einheit passt nicht, d.h. k=1 ist nicht korrekt.
Dennoch kann man k mit Einheit als Summationsindex auffassen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Nescio

Anmeldungsdatum: 05.12.2015
Beiträge: 279
|
 Nescio Verfasst am: 14. Aug 2019 14:47 Titel: Nescio Verfasst am: 14. Aug 2019 14:47 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Dennoch kann man k mit Einheit als Summationsindex auffassen. |
Wenn man mit dem Kopf durch die Wand will kann man das so machen. Das ist aber sehr ungewöhnlich und wird garantiert für Verwirrung sorgen. Ich finde das ist nicht hilfreich und hat auch nichts mit der originalen Fragestellung zu tun. |
|
 |
|
















 )
) was genau hat dich an der Summe gestört jh? Ist die wegen doppelter Nutzung von k falsch gewesen oder was passte dort nicht?
was genau hat dich an der Summe gestört jh? Ist die wegen doppelter Nutzung von k falsch gewesen oder was passte dort nicht?