| Autor |
Nachricht |
ixviar
Gast
|
 ixviar Verfasst am: 08. Nov 2014 20:26 Titel: Fouriertransformation Gaußsches Wellenpaket ixviar Verfasst am: 08. Nov 2014 20:26 Titel: Fouriertransformation Gaußsches Wellenpaket |
 |
|
Meine Frage:
Hallo,
ich soll folgende Fouriertransformation durchführen:
 = \int_ {-\infty} ^\infty dk A \quad e^{-(k-k_0 )^2 / 2\sigma_k^2}\quad e^{i(kx-\omega t)} )
mit
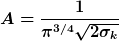
und
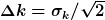
Und aus diesem Ergebnis die Heisenbergsche Unschärferelation 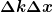 berechnen. berechnen.
Ich komme aber bei der Fouriertransformation nicht weiter.
Meine Ideen:
Ich denke man kann A aus dem integral ziehen, weil diese ja konstant ist(?) -> Ist 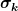 denn eine konstante bzw. denn eine konstante bzw. 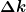 ?? Weil sonst würde das ja nicht funktionieren. ?? Weil sonst würde das ja nicht funktionieren.
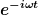 kann ich doch auch aus dem Integral ziehen, weil dieser Term ja nicht von k abhängt oder? kann ich doch auch aus dem Integral ziehen, weil dieser Term ja nicht von k abhängt oder?
Nun muss ich nur noch das restliche integrieren, wobei ich mir schwer tue.
Ich frage mich überhaupt noch, woher ich dann mein konkretes 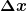 und und 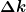 herbekomme... herbekomme...
LG |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18015
|
 TomS Verfasst am: 08. Nov 2014 23:20 Titel: TomS Verfasst am: 08. Nov 2014 23:20 Titel: |
 |
|
Du musst im Exponenten eine quadratische Ergänzung vornehmen und anschließend geeignet substituieren.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 08. Nov 2014 23:51 Titel: ixviar Verfasst am: 08. Nov 2014 23:51 Titel: |
 |
|
Ok, aber stimmen meine anderen Sachen? Also steht im endeffekt nur noch das Integral von der e-Funktion da?
Lg |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 09. Nov 2014 10:39 Titel: ixviar Verfasst am: 09. Nov 2014 10:39 Titel: |
 |
|
Also ich habe jetzt folgendes Integral:
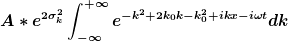
den quadratischen Term mit 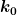 kann ich herausziehen, ja. Aber was ist mit dem gemischen term? kann ich herausziehen, ja. Aber was ist mit dem gemischen term?
Die quadratische ergänzung muss ja den komplexen Term 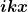 mitnehmen oder? Der gemischte Term mit mitnehmen oder? Der gemischte Term mit 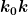 steht mir aber noch im weg :/ steht mir aber noch im weg :/
Was ist eigentlich mit dem 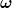 ? Dieser hängt doch auch von k ab!? ? Dieser hängt doch auch von k ab!?
LG  |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18015
|
 TomS Verfasst am: 09. Nov 2014 10:52 Titel: TomS Verfasst am: 09. Nov 2014 10:52 Titel: |
 |
|
Du hast bei den Rechenregeln im Exponenten irgendwas falsch gemacht, jedenfalls kann der Vorfaktor des Integrals nicht stimmen. Vorher hattest du im Exponenten dein sigma im Nenner, jetzt steht es auf einmal ohne k vor dem Integral. Wie geht das?
Zur quadratischen Ergänzung: wenn du im Exponenten soetwas wie
)
stehen hast, dann musst du das auf eine Form
^2 + d)
bringen, wobei auch komplexe Zahlen auftreten können. Die Konstanten k-bar und d musst du geeignet bestimmen.
Anschließend substituierst du
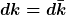
und kannst das Gaußsche Integral ganz normal lösen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 09. Nov 2014 11:12 Titel: ixviar Verfasst am: 09. Nov 2014 11:12 Titel: |
 |
|
Dankeschön für Deine Antwort.
Zum Vorfaktor des Integrals:
Ich verstehe, ich habe das falsch heraus gezogen... Kann man das überhaupt herausziehen,ich denke nicht. Naja dann ist es eben nur eine Konstante, die ich mit in die quadratische Ergänzung bringen muss:)
Also ich muss jetzt auf jeden Fall diesen Term quadratisch Ergänzen oder?:
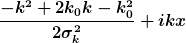
Ich habe  ) und und 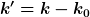 gesetzt und komme nun auf die Form: ( mit gesetzt und komme nun auf die Form: ( mit 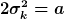 ) )
 x - \frac{2k'^2}{a} )
Wenn dieser Term stimmt, dann muss ich nun quadratisch ergänzen und kann das Integral dann lösen oder?
LG |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 09. Nov 2014 11:43 Titel: jh8979 Verfasst am: 09. Nov 2014 11:43 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Anschließend substituierst du
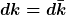
und kannst das Gaußsche Integral ganz normal lösen. |
Das denkt man sich so und es wird leider auch sehr sehr oft so gemacht, weil zufällig(?) das richtige rauskommt. Aber um das Integral korrekt zu loesen muss man den Residuensatz anwenden, da es sich um eine Integration in der komplexen Ebene handelt:
Seite 8, Kapitel 7.: http://people.reed.edu/~jerry/311/lec08.pdf
Es gibt auch einen eleganten Beweis, der das Problem auf eine DGL zurückführt:
http://www.cse.yorku.ca/~kosta/CompVis_Notes/fourier_transform_Gaussian.pdf
(dabei benutzt er nur die Eigenschaften 106 und 107 von hier) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18015
|
 TomS Verfasst am: 09. Nov 2014 11:50 Titel: TomS Verfasst am: 09. Nov 2014 11:50 Titel: |
 |
|
Du startest mit
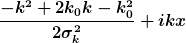
Schreib das doch als
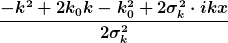
Jetzt die Terme nach Potenzen von k zusammenfassen und quadratisch ergänzen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 09. Nov 2014 12:06 Titel: ixviar Verfasst am: 09. Nov 2014 12:06 Titel: |
 |
|
Danke für die Hilfe!
Ich hab mir jetzt schon die Mühe gemacht und mit meinem Term die quadratische Ergänzung gemacht und vereinfacht (stimmt doch auch so oder?):
 = A e^{\frac{1}{4} \sigma_k^2+k_0^2/2\sigma_k^2} \int_{-\infty}^{+\infty} exp[ \frac{(k'- \frac{1}{2} i \sigma_k^2)^2}{\sigma_k^2} - i \omega t] dk')
Wenn das nun totaler quatsch ist... dann mache ichs natürlich mit Deinem Ansatz 
Jetzt fehlt nur noch der Term mit dem 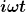
Was stell ich denn mit dem an  ? ?
LG |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18015
|
 TomS Verfasst am: 09. Nov 2014 13:07 Titel: TomS Verfasst am: 09. Nov 2014 13:07 Titel: |
 |
|
Der Vorfaktor ist wieder falsch. Die 2 im Nenner (im Integral) fehlt. Dein x ist verschwunden.
Ich weiß nicht, was du da treibst.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 09. Nov 2014 13:28 Titel: ixviar Verfasst am: 09. Nov 2014 13:28 Titel: |
 |
|
hey,
Es fehlt keine 2 im Nenner, das habe ich vorher herausgekürzt. Aber egal.
Das x fehlt tatsächlich  ... sorry. ... sorry.
Naja ich habe mal nach deiner Form eine quadratische Ergänzung durchgeführt:
Ergebnis: )^2 - (k_0 + i \sigma_k^2 x)^2 - k_0 ^2 )
Das ganze natürlich noch durch 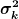 geteilt!! geteilt!!
Nun kann ich alle "konstanten" aus dem Integral ziehen und dann so substituieren, dass nur noch ein 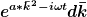 (Mit a als vorfaktor ) zu integrieren ist oder? (Mit a als vorfaktor ) zu integrieren ist oder?
Lg
Sorry für meine Unfähigkeit ...  |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18015
|
 TomS Verfasst am: 09. Nov 2014 13:34 Titel: TomS Verfasst am: 09. Nov 2014 13:34 Titel: |
 |
|
| ixviar hat Folgendes geschrieben: | | Es fehlt keine 2 im Nenner, das habe ich vorher herausgekürzt. |
Schau dir mal bitte deinen ersten Beitrag und im Integral den k^2-Term an. Da hast du ein 1/2.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18015
|
 TomS Verfasst am: 09. Nov 2014 13:37 Titel: TomS Verfasst am: 09. Nov 2014 13:37 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Anschließend substituierst du
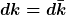
und kannst das Gaußsche Integral ganz normal lösen. |
Sorry, das ist falsch. Es muss lauten
 = dk^\prime)
D.h. du musst im Komplexen verschieben (jh8979 hat ansonsten natürlich recht)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 09. Nov 2014 13:55 Titel: ixviar Verfasst am: 09. Nov 2014 13:55 Titel: |
 |
|
So, jetzt komme ich letztendlich auf:
 = A exp[ \frac{-(k_0 + i\sigma_k^2x)^2 - k_0^2}{2\sigma_k^2}] \int_{-\infty}^{+\infty} exp[ \frac{-(k-(k_0 + i\sigma_k^2x))^2}{2\sigma_k^2 } - i \omega t] dk )
Wenn das nun falsch ist, dann will ich Dich nicht mehr damit nerven, tut mir echt leid...
Falls das stimmt, dann muss ich nun nur noch das Integral durch Substitution lösen... zb mit: ) )
LG |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 09. Nov 2014 15:31 Titel: jh8979 Verfasst am: 09. Nov 2014 15:31 Titel: |
 |
|
| ixviar hat Folgendes geschrieben: |
 = A exp[ \frac{-(k_0 + i\sigma_k^2x)^2 - k_0^2}{2\sigma_k^2}] \int_{-\infty}^{+\infty} exp[ \frac{-(k-(k_0 + i\sigma_k^2x))^2}{2\sigma_k^2 } - i \omega t] dk )
|
Das allererste Vorzeichen in der Exponentialfunktion vor dem Integral ist falsch.Wenn ich (= Mathematica  ) mich nicht verrechnet hab, dann sollte da ein Plus stehen : ) mich nicht verrechnet hab, dann sollte da ein Plus stehen :
 = A e^{ \frac{+(k_0 + i\sigma_k^2x)^2 - k_0^2}{2\sigma_k^2} } \int_{-\infty}^{+\infty}\!\! dk \, \,e^{= \frac{(k-(k_0 + i\sigma_k^2x))^2}{2\sigma_k^2 } - i \omega t} )
| Zitat: |
Falls das stimmt, dann muss ich nun nur noch das Integral durch Substitution lösen... zb mit: ) )
|
Wie schon weiter oben geschrieben geht das nicht wirklich mit Substitution (überleg Dir mal was mit den Grenzen passieren würde), sondern per Residuensatz (was dann dasselbe Ergebnis liefert, wie die naive und falsche Substitution).
Wie das genau geht, steht z.B. in dem Link, aus meinem ersten Post. |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 09. Nov 2014 15:49 Titel: ixviar Verfasst am: 09. Nov 2014 15:49 Titel: |
 |
|
Stimmt, da gehört ein plus hin, danke!
Also in der Angabe steht, ich soll das integral mit dem Normierungsintegral lösen:
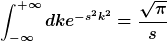
Ich habe nun das Wellenpaket so berechnet und bekomme für das Wellenpaket AM ZEITPUNKT t=0 (Aufgabenstellung) :
 = \frac{\sqrt{\sigma_k}}{\pi^{1/4}}e^{-\sigma_k^2x^2 + 2 i x k_0} )
Das 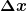 soll ich nun aus dem Betragsquadrat: soll ich nun aus dem Betragsquadrat:
 |^2 = \psi(x,0) \psi(x,0) * ) bekommen. bekommen.
Ich habe das ausgerechnet und komme auf:
 |^2 = \frac{\sigma_k e^{-2\sigma_k x^2}}{\sqrt{\pi}} )
Ich schätze mal da ist wieder irgendwas falsch... 
Aber das Problem mit dem 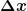 hat sich noch nicht geklärt! Ich soll ja hat sich noch nicht geklärt! Ich soll ja 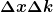 letztendlich berechnen. letztendlich berechnen.
LG |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 09. Nov 2014 15:58 Titel: jh8979 Verfasst am: 09. Nov 2014 15:58 Titel: |
 |
|
|
Abgesehen davon, dass diese Substitution so falsch ist (wenn auch vielfach so gezeigt) und dass man mit dem Residuensatz begründen muss wieso das Integral und das Normierungsintegral gleich sind, ist das Ergebnis bis auf ein Faktor 1/2 im Exponenten richtig. |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 09. Nov 2014 16:20 Titel: ixviar Verfasst am: 09. Nov 2014 16:20 Titel: |
 |
|
Ok, dankeschön. Ich glaube, dass es nicht beabsichtigt war, dass wir solche Sätze anwenden (3. sem BA physik)
Wie komme ich jetzt auf das 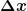
In der Aufgabenstellung steht, dass wir dieses aus dem betragsquadrat bekommen sollen... wie soll das denn funktionieren?
LG |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 09. Nov 2014 16:33 Titel: jh8979 Verfasst am: 09. Nov 2014 16:33 Titel: |
 |
|
| ixviar hat Folgendes geschrieben: | Ok, dankeschön. Ich glaube, dass es nicht beabsichtigt war, dass wir solche Sätze anwenden (3. sem BA physik)
|
Ob beabsichtigt oder nicht: So wie Du es jetzt gemacht hast (und wohl auch machen solltest), ist die Herleitung falsch. Die Substitution führt auf einen Integrationsweg, der im komplexen liegt (wie man an den Grenzen schoen erkennen kann).
[Der Residuensatz kommt oft schon im 2ten Semester in "Mathematische Methoden" dran.]
| Zitat: |
Wie komme ich jetzt auf das 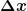
In der Aufgabenstellung steht, dass wir dieses aus dem betragsquadrat bekommen sollen... wie soll das denn funktionieren?
|
Welche der Parameter bestimmt denn, wie sehr Deine Wellenfunktion ausgedehnt ist? Oder anders: woher kommt denn Dein ∆k ? |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 09. Nov 2014 16:46 Titel: ixviar Verfasst am: 09. Nov 2014 16:46 Titel: |
 |
|
Also die Breite müsste doch das Intervall zwischen zwei Nullstellen der EINHÜLLENDEN Welle sein oder?
Das deltaK ist ja schon in der Angabe definiert.
Ich verstehe nur nicht, warum ich das betragsquadrat berechnen sollte.
Wenn ich das Betragsquadrat der Welle über die beiden Nullstellen Integriere, so müsste ich doch die Wahrscheinlichkeit 1 haben oder?
also:
 |^2 = 1)
LG |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 09. Nov 2014 16:48 Titel: jh8979 Verfasst am: 09. Nov 2014 16:48 Titel: |
 |
|
Viel Spass beim Nullstellen bestimmen 
Ja ∆k ist schon gegeben, aber wieso hat es den Wert den es hat? Theoretisch hättest Du das auch aus der Wellenfunktion berechnen können. |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 09. Nov 2014 16:57 Titel: ixviar Verfasst am: 09. Nov 2014 16:57 Titel: |
 |
|
Ich weiß nicht, wie ich sonst vorgehen soll. In der Vorlesung haben wir aus einer Rechteckswelle das so gemacht.
Das Delta k ergibt sich doch aus den Überlagerung der Partialwellen oder?
Zum Glück ist es gegeben 
Also mit der normierung des Betragsquadrats komm ich auch nicht weiter, weil das eine hässlliche integration eines gauß integrals wäre...
lg |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 09. Nov 2014 17:13 Titel: jh8979 Verfasst am: 09. Nov 2014 17:13 Titel: |
 |
|
Wenn Du die Normierung ausrechnen willst benutzt Du am besten den Satz von Parseval (hochtrabender Name für die Aussage: Die Normierung ändert sich nicht (oder nur um 2*pi) unter Fouriertransformation  ) )
http://de.wikipedia.org/wiki/Satz_von_Parseval#Anwendungen
Mach Dir doch mal eine Skizze Deiner Wellenfunktion, vllt kommst Du dann darauf was ∆k ist (und später dann ∆x). |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 09. Nov 2014 17:31 Titel: ixviar Verfasst am: 09. Nov 2014 17:31 Titel: |
 |
|
Also meine Verteilung der Wellenzahlen gehen ja von minus unendlich bis plus unendlich, deswegen ist doch ein delta k bei mir nicht wirklich definiert oder  ... ...
Das Delta x ergibt sich ja dann aus der Wahrscheinlichkeitsverteilung des Betragsquadrats.. Also muss ich irgendwie einen Zusammenhang zwischen delta x und dem Betragsquadrat haben... über die normierung bekomme ich ja kein delta x mit rein, weil das integral zwischen -infty und +infty verläuft und nicht in meinen vorher festgelegten grenzen.. (d.h. delta x ist auch nicht definiert wegen den uneigentlichen grenzen  ) ) |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 09. Nov 2014 17:34 Titel: jh8979 Verfasst am: 09. Nov 2014 17:34 Titel: |
 |
|
|
Zeichne doch mal die Funktion... vllt ist es dann klarer... |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 09. Nov 2014 17:49 Titel: ixviar Verfasst am: 09. Nov 2014 17:49 Titel: |
 |
|
Das habe ich.
Die Betragsquadrat Funktion ist eine Gaußsche Kurve um x=0 ohne Nullstelle.
Soll ich denn eine "eigene"Gaußsche Funktion um x=0"erzeugen" die 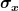 enthält? enthält?
also:
 |^2 = \frac{1}{\sigma_x \sqrt{2\pi}}e^{-\frac{1}{2} (\frac{x}{\sigma_x})^2} )
und dann beide vergleichen? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 09. Nov 2014 17:52 Titel: jh8979 Verfasst am: 09. Nov 2014 17:52 Titel: |
 |
|
|
Du hast doch ausgerechnet was die FT ist.. was willst Du jetzt noch erzeugen? Siehst Du auch was ∆k ist in Deiner Zeichnung? |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 09. Nov 2014 17:58 Titel: ixviar Verfasst am: 09. Nov 2014 17:58 Titel: |
 |
|
ich versuche damit einen zusammenhang zwischen 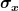 und und 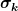 zu erzeugen .......... Das mit dem delta k habe ich trotz zeichnung immer noch nicht verstanden, weil es meiner meinung nach uneigentlich ist. zu erzeugen .......... Das mit dem delta k habe ich trotz zeichnung immer noch nicht verstanden, weil es meiner meinung nach uneigentlich ist.
Und die FT im Betragsquadrat ergibt eine Verteilung um x=0 die ich mit delta x ausdrücken kann, da es eine gaußverteilung ist...
weiter weiß ich einfach net |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 09. Nov 2014 18:08 Titel: jh8979 Verfasst am: 09. Nov 2014 18:08 Titel: |
 |
|
| ixviar hat Folgendes geschrieben: | ich versuche damit einen zusammenhang zwischen 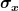 und und 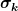 zu erzeugen .......... zu erzeugen .......... |
Ok. Dann mach das. Die Idee dahinter ist richtig (wenn ich Dich richtig verstehe  ). ). |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 09. Nov 2014 18:20 Titel: ixviar Verfasst am: 09. Nov 2014 18:20 Titel: |
 |
|
Naja.. ich weiß nicht ob das stimmt aber ich komme auf:

und weil gilt: 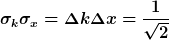
lg |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8576
|
 jh8979 Verfasst am: 09. Nov 2014 19:07 Titel: jh8979 Verfasst am: 09. Nov 2014 19:07 Titel: |
 |
|
|
Dir ist irgendwie ein √2 verloren gegangen (vermutlich die 1/2 die ich oben schon meinte). Es sollte ∆k ∆x = 1/2 rauskommen. |
|
 |
ixviar
Gast
|
 ixviar Verfasst am: 09. Nov 2014 19:08 Titel: ixviar Verfasst am: 09. Nov 2014 19:08 Titel: |
 |
|
Ok, das könnte gut sein 
Vielen Dank für die Hilfe!
LG |
|
 |
|

















 ... sorry.
... sorry.

 ) mich nicht verrechnet hab, dann sollte da ein Plus stehen :
) mich nicht verrechnet hab, dann sollte da ein Plus stehen :

 ...
...
 )
)