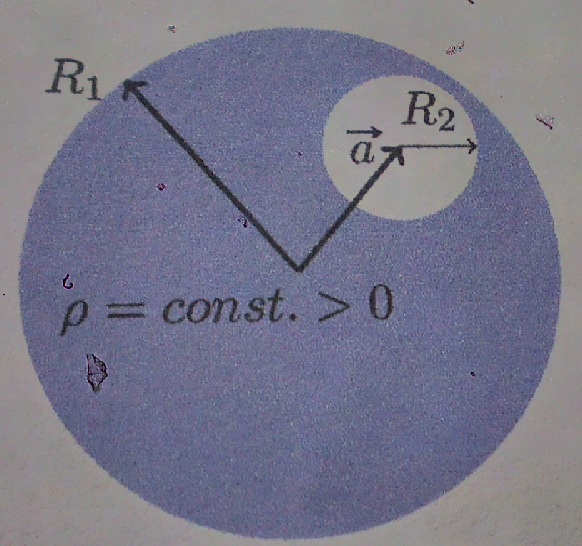| Autor |
Nachricht |
St3fan
Anmeldungsdatum: 25.05.2015
Beiträge: 19
Wohnort: Hamburg
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 31. Okt 2015 09:47 Titel: isi1 Verfasst am: 31. Okt 2015 09:47 Titel: |
 |
|
In der Vollkugel (Radius r) hätten wir die Ladung Q = V*ρ = 4/3 r³pi ρ
Eine Ldung Q hat bekanntlich das Feld E = Q / (4pi ε0 r²) = 3,76E10 m/F * r * ρ (r als Vektor).
Die gleiche Formel für die ausgeschnittenen Kugel mit dem Mittelpunkt vek{a} und negativem ρ.
Wird mathematisch etwas mühselig, oder?
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 31. Okt 2015 15:33 Titel: GvC Verfasst am: 31. Okt 2015 15:33 Titel: |
 |
|
| isi1 hat Folgendes geschrieben: | | Wird mathematisch etwas mühselig, oder? |
Möglicherweise lautet die Aufgabenstellung ja ein bisschen anders, als vom Fragesteller hier wiedergegeben. Man sollte ihn deshalb erstmal nach dem originalen Wortlaut der Aufgabenstellung fragen. Sollte das aber die originale Aufgabenstellung sein, wird es in der Tat etwas mühsam.
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 31. Okt 2015 18:19 Titel: Re: Gaußsches Gesetz, Kugel mit Kugelausschnitt Bestimmung v jh8979 Verfasst am: 31. Okt 2015 18:19 Titel: Re: Gaußsches Gesetz, Kugel mit Kugelausschnitt Bestimmung v |
 |
|
| St3fan hat Folgendes geschrieben: |
Muss ich das jetzt für die Vollkugel (mit 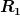 und und 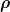 ) ausrechnen und getrennt für die ausgeschnittene Kugel (mit ) ausrechnen und getrennt für die ausgeschnittene Kugel (mit 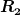 und und 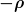 ) und die beiden Ergebnisse dann addieren? ) und die beiden Ergebnisse dann addieren? |
Ja das ist richtig.
Ich weiss auch nicht wieso die beiden anderen meinen, dass dies mathematisch mühselig wäre. Ich glaub das ist sogar ziemlich trivial, aber vllt ueberseh ich ja was.
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 31. Okt 2015 18:39 Titel: Re: Gaußsches Gesetz, Kugel mit Kugelausschnitt Bestimmung v isi1 Verfasst am: 31. Okt 2015 18:39 Titel: Re: Gaußsches Gesetz, Kugel mit Kugelausschnitt Bestimmung v |
 |
|
| jh8979 hat Folgendes geschrieben: | | Ich weiss auch nicht wieso die beiden anderen meinen, dass dies mathematisch mühselig wäre. Ich glaub das ist sogar ziemlich trivial, aber vllt ueberseh ich ja was. |
Wenn Du das behauptest, wissen wir aus Erfahrung, dass Du fast immer recht hast, JH.
Magst Du uns mal bitte zeigen, wie's einfach geht?
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 31. Okt 2015 18:47 Titel: Re: Gaußsches Gesetz, Kugel mit Kugelausschnitt Bestimmung v jh8979 Verfasst am: 31. Okt 2015 18:47 Titel: Re: Gaußsches Gesetz, Kugel mit Kugelausschnitt Bestimmung v |
 |
|
Genau so:
| St3fan hat Folgendes geschrieben: |
Muss ich das jetzt für die Vollkugel (mit 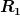 und und 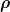 ) ausrechnen und getrennt für die ausgeschnittene Kugel (mit ) ausrechnen und getrennt für die ausgeschnittene Kugel (mit 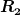 und und 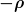 ) und die beiden Ergebnisse dann addieren? ) und die beiden Ergebnisse dann addieren? |
Das Einzige was man wissen muss, ist wie das Feld im Inneren einer homogen geladenen Kugel aussieht. Der Rest der Rechnung ist ein Zweizeiler. Die Tatsache dass man nur das Feld im Hohlraum will, macht das Ergebnis besonders einfach.
PS: Das ist im Übrigen eine Standardaufgabe in der Elektrostatik, um die Macht des Superpositionsprinzips zu zeigen.
|
|
 |
St3fan
Anmeldungsdatum: 25.05.2015
Beiträge: 19
Wohnort: Hamburg
|
 St3fan Verfasst am: 31. Okt 2015 19:09 Titel: St3fan Verfasst am: 31. Okt 2015 19:09 Titel: |
 |
|
Also das ist der originale Wortlaut der Aufgabe und der Titel ist der Gleiche wie von der Aufgabe auch.
Wir sollen die Aufgabe mit dem Gauß'schen Satz lösen.
Ich hab es jetzt mal versucht und komme auf das gleiche Ergebnis wie isi1
Ich habe das Feld der Ganzen Kugel 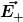 genannt und das Feld der kleinen in der großen genannt und das Feld der kleinen in der großen 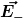 genannt: genannt:

Und für die kleine Kugel enthalte ich dementsprechend:
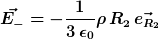
Nach dem Superpositionsprinzip muss ich doch jetzt
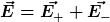
machen.
Aber woran erkenne ich denn das Feld nur in dem kleinen Hohlraum?
Zuletzt bearbeitet von St3fan am 31. Okt 2015 19:18, insgesamt einmal bearbeitet |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 31. Okt 2015 19:17 Titel: jh8979 Verfasst am: 31. Okt 2015 19:17 Titel: |
 |
|
| St3fan hat Folgendes geschrieben: |
Nach dem Superpositionsprinzip muss ich doch jetzt
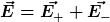
machen. |
Dann mach doch.
| Zitat: |
Aber woran erkenne ich denn das Feld nur in dem kleine Hohlraum? |
Ich versteh die Frage nicht.
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 31. Okt 2015 19:22 Titel: isi1 Verfasst am: 31. Okt 2015 19:22 Titel: |
 |
|
Vielleicht E(x,y,z) = k * ( (1/ε_r)*√(x²+y²+z²) - √((x-x₁)²+(y-y₁)²+(z-z₁)²) ?
Scheint mir nicht gerade simpel.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 31. Okt 2015 19:24 Titel: jh8979 Verfasst am: 31. Okt 2015 19:24 Titel: |
 |
|
| isi1 hat Folgendes geschrieben: | Vielleicht E(x,y,z) = k * ( (1/ε_r)*√(x²+y²+z²) - √((x-x₁)²+(y-y₁)²+(z-z₁)²) ?
Scheint mir nicht gerade simpel. |
Man kann die einzelnen Komponenten Ex, Ey und Ez auch noch getrennt aufschreiben, um es möglichst kompliziert zu machen...
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 31. Okt 2015 19:26 Titel: isi1 Verfasst am: 31. Okt 2015 19:26 Titel: |
 |
|
Meine Gleichung stimmt ohnehin nicht, da ich die Vektoreigenschaft nicht berücksichtigt habe.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
St3fan
Anmeldungsdatum: 25.05.2015
Beiträge: 19
Wohnort: Hamburg
|
 St3fan Verfasst am: 31. Okt 2015 19:41 Titel: St3fan Verfasst am: 31. Okt 2015 19:41 Titel: |
 |
|
Ich hab jetzt raus:
 = \frac{1}{3 \, \epsilon_0} \rho \, \left ( \vec{R_1}-\vec{R_2} \right ))
Nur weiß ich ehrlich gesagt nicht was für ein Feld ich damit angebe...
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 31. Okt 2015 19:43 Titel: jh8979 Verfasst am: 31. Okt 2015 19:43 Titel: |
 |
|
|
R1 und R2 hängen zusammen, das vereinfacht das Ergebnis nochmal etwas.
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 31. Okt 2015 19:57 Titel: isi1 Verfasst am: 31. Okt 2015 19:57 Titel: |
 |
|
Aha
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ
Zuletzt bearbeitet von isi1 am 23. Jan 2016 18:57, insgesamt einmal bearbeitet |
|
 |
St3fan
Anmeldungsdatum: 25.05.2015
Beiträge: 19
Wohnort: Hamburg
|
 St3fan Verfasst am: 31. Okt 2015 20:14 Titel: St3fan Verfasst am: 31. Okt 2015 20:14 Titel: |
 |
|
Die hängen zusammen?
Mir würde jetzt nur einfallen, dass sie mit einem Vektor 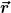 zusammenhängen, so dass: zusammenhängen, so dass:
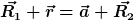
und somit:
=
<br />
\frac{1}{3 \, \epsilon_0} \rho \, \left ( \vec{a}+\vec{r} \right ))
Aber das vereinfacht nichts und nun ist da noch ein unbekannter Vektor drin...
|
|
 |
St3fan
Anmeldungsdatum: 25.05.2015
Beiträge: 19
Wohnort: Hamburg
|
 St3fan Verfasst am: 31. Okt 2015 20:18 Titel: St3fan Verfasst am: 31. Okt 2015 20:18 Titel: |
 |
|
|
Zu Isi1: der r_2, zeigt der auf einen bestimmten Punkt oder auf den Rand der großen Kugel?
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 31. Okt 2015 20:19 Titel: isi1 Verfasst am: 31. Okt 2015 20:19 Titel: |
 |
|
| St3fan hat Folgendes geschrieben: | | Zu Isi1: der r_2, zeigt der auf einen bestimmten Punkt oder auf den Rand der Kugel? |
Der kann auf irgend einen (Mess-)Punkt P innerhalb der kleinen Kugel zeigen (siehe meine Zeichnung oben).
Es hat mich schon immer gewundert, dass in der dielektrischen Kugel im konstanten Feld die Feldlinien genau gerade und parallel verlaufen (also E konstant ist), während sie außerhalb natürlich ordentlich verformt werden.
In Deinem Fall scheint demnach E im ganzen Hohlraum konstant und gleich dem Feld im Mittelpunkt der kleinen Kugel zu sein.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
St3fan
Anmeldungsdatum: 25.05.2015
Beiträge: 19
Wohnort: Hamburg
|
 St3fan Verfasst am: 31. Okt 2015 20:37 Titel: St3fan Verfasst am: 31. Okt 2015 20:37 Titel: |
 |
|
Ich guck die ganze Zeit auf dein Bild und deinen Text aber ich kann deinen Ahhaa Moment nich nachvollziehen 
Wie hängen denn dadurch die Vektoren R_1 und R_2 zusammen?
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 31. Okt 2015 20:44 Titel: isi1 Verfasst am: 31. Okt 2015 20:44 Titel: |
 |
|
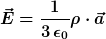
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ
Zuletzt bearbeitet von isi1 am 23. Jan 2016 18:59, insgesamt einmal bearbeitet |
|
 |
St3fan
Anmeldungsdatum: 25.05.2015
Beiträge: 19
Wohnort: Hamburg
|
 St3fan Verfasst am: 31. Okt 2015 20:54 Titel: St3fan Verfasst am: 31. Okt 2015 20:54 Titel: |
 |
|
Das versteh ich nicht, Zeigt der 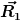 nicht immer zum Rand der großen Kugel mit der länge nicht immer zum Rand der großen Kugel mit der länge 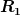 ? ?
Oder zeigt der in den gesamten Raum in der großen Kugel?
Oder wurde die Kugel jetzt einfach so gewählt das es mit 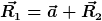 passt? passt?
|
|
 |
St3fan
Anmeldungsdatum: 25.05.2015
Beiträge: 19
Wohnort: Hamburg
|
 St3fan Verfasst am: 31. Okt 2015 22:26 Titel: St3fan Verfasst am: 31. Okt 2015 22:26 Titel: |
 |
|
Ok, ich habe jetzt im Großen und ganzen das Problem verstanden. Das einzige was mich noch verwirrt, ist der Tipp von unseren Professor.
Warum kann ich annehmen, dass die Ladingsdichte der kleinen Kugel 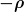 ist? ist?
|
|
 |
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2903
Wohnort: München
|
 isi1 Verfasst am: 31. Okt 2015 22:36 Titel: isi1 Verfasst am: 31. Okt 2015 22:36 Titel: |
 |
|
| St3fan hat Folgendes geschrieben: | Warum kann ich annehmen, dass die Ladingsdichte der kleinen Kugel 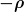 ist? ist? |
Wenn wir die große Kugel ganz mit Ladung füllen, haben wir zuviel Ladung, nämlich den Raum der kleinen Kugel. Also nehmen wir die kleine Kugel mit minus rho an, dann hebt sich in der kleinen Kugel dieses Minus mit dem Plus der großen Kugel auf, sodass wir in diesem Bereich weisungsgemäß die Ladung Null haben.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
 |
St3fan
Anmeldungsdatum: 25.05.2015
Beiträge: 19
Wohnort: Hamburg
|
 St3fan Verfasst am: 31. Okt 2015 22:51 Titel: St3fan Verfasst am: 31. Okt 2015 22:51 Titel: |
 |
|
|
Ahh Ok, jetzt versteh ich es. Vielen Dank für die tolle Hilfe und der Geduld mit mir.
|
|
 |
|