| Autor |
Nachricht |
sterni17
Anmeldungsdatum: 17.10.2022
Beiträge: 3
|
 sterni17 Verfasst am: 17. Okt 2022 22:25 Titel: Integral für Beschleunigung aufstellen sterni17 Verfasst am: 17. Okt 2022 22:25 Titel: Integral für Beschleunigung aufstellen |
 |
|
Hey Leute,
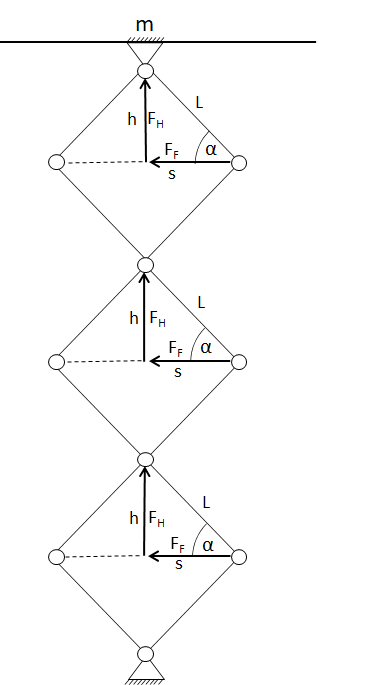
ich habe eine Frage zu einem System, was ich mir gerade angucke. Eine Prinzipskizze habe ich angehangen.
In diesem dynamischen System wird durch Zugfedern eine Hubkraft FH generiert. Die Federkraft ist F_F in der Skizze, der Federweg s. Die Federn sind am Anfang gespannt, das System zusammen geklappt und der Winkel alpha dementsprechend klein. Wenn das System ausgelöst wird, soll die Federn zusammen gezogen werden, alpha wird größer und eine Kraft nach oben wird generiert, die eine Masse auf der Platte oben beschleunigt. Dabei möchte ich sehen, wie meine Kraft F_H von den Federn abhängt und wie ich die Beschleunigung berechne bzw das die Geschwindigkeit über das Integral.
Die Kraft ist von Federkraft, die sich über den Federweg s ändert, und vom Winkel alpha abhängig. Damit ist meine Beschleunigung nicht konstant. Mein Ansatz:
 = F_F(t) \cdot tan(\alpha (t)) = F_F(t) \cdot \dfrac{sin(\alpha (t))}{cos(\alpha (t)} = F_F(t) \cdot \dfrac{dh}{ds} )
Über Pythagoras bekomme ich:
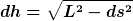
Und über die Federkonstante D:
 = D \cdot ds )
 = D \cdot ds \cdot \dfrac{ \sqrt{L^2 - ds^2}}{ds} = D \cdot \sqrt{L^2 - ds^2} = D \cdot dh )
Am Ende hätte ich nur eine Abhängigkeit von der Federkonstante zu dh bzw zu ds über Pythagoras und ich kann mir irgendwie nicht vorstellen, dass es ein so vereinfachtes Ergebnis ist. Was übersehe ich? Über jede Hilfe wäre ich dankbar. Am Ende möchte ich die Kraft über den Weg integrieren, um meine Energie zu errechnen und die Beschleunigung bilden mit:
 = \dfrac{F_H (t)}{m} )
um über Integral auf meine Geschwindigkeit zu kommen.
Vielen Dank und liebe Grüße!
| Beschreibung: |
|
| Dateigröße: |
13.3 KB |
| Angeschaut: |
1730 mal |
|
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 18. Okt 2022 15:06 Titel: Mathefix Verfasst am: 18. Okt 2022 15:06 Titel: |
 |
|
Ich betrachte 1 Hubelement:
l_f = Jeweilige Länge der Feder

 = \frac{h}{l_f} \rightarrow F_h = F_f\cdot \frac{h}{l_f} )


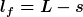
 = F_f\cdot \sqrt{\frac{L^{2}}{(L - s)^{2}} -1} )
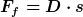
 = \frac{ D \cdot s \cdot \sqrt{\frac{L^{2}}{(L - s)^{2}} -1}}{m} )
|
|
 |
sterni17
Anmeldungsdatum: 17.10.2022
Beiträge: 3
|
 sterni17 Verfasst am: 18. Okt 2022 15:41 Titel: sterni17 Verfasst am: 18. Okt 2022 15:41 Titel: |
 |
|
Hey,
vielen Dank für deine Antwort.
Ich hätte zwei Fragen zu der Rechnung:
1) Wieso hast du den Federweg s mit l_f ersetzt und wieso ist l_f = L-s?
2) Ich habe jetzt ja die Beschleunigung von s abhängig. Wenn ich das integriere bekomme ich aber nicht die Geschwindigkeit, weil ich das ganze zeitlich abhängig machen müsste oder? Wenn ich Fh über s integriere, ist das meine potentielle Energie oder sollte ich das dann nochmal von h abhängig machen?
Vielen Dank und beste Grüße.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 18. Okt 2022 16:06 Titel: Mathefix Verfasst am: 18. Okt 2022 16:06 Titel: |
 |
|
| sterni17 hat Folgendes geschrieben: | Hey,
vielen Dank für deine Antwort.
Ich hätte zwei Fragen zu der Rechnung:
1) Wieso hast du den Federweg s mit l_f ersetzt und wieso ist l_f = L-s?
2) Ich habe jetzt ja die Beschleunigung von s abhängig. Wenn ich das integriere bekomme ich aber nicht die Geschwindigkeit, weil ich das ganze zeitlich abhängig machen müsste oder? Wenn ich Fh über s integriere, ist das meine potentielle Energie oder sollte ich das dann nochmal von h abhängig machen?
Vielen Dank und beste Grüße. |
zu Frage 1) Im vollständig gespannten Zustand hat die Feder die Länge L (L liegt horizontal) und h ist gleich 0.
Wird die Feder um den Betrag s entspannt, beträgt ihre Länge l_f = L - s und damit h = (L - s) * tan(alpha).
Zu Frage 2)
a(t) ist gesucht. Kann über s(t) ermittelt werden. Über die Herleitung muss ich noch nachdenken. Habe eine Idee, aber es kann etwas dauern.
Gruss
Mathefix
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 18. Okt 2022 18:00 Titel: Myon Verfasst am: 18. Okt 2022 18:00 Titel: |
 |
|
Die zeitliche Entwicklung könnte man grundsätzlich auf diesem Weg herleiten:
Aus der Energieherhaltung
-E_F(s)-W_H(s))
(E_F=in den Federn gespeicherte Spannenergie; W_H=geleistete Hubarbeit) kann man h(t) durch Integration erhalten
-E_F(s)-W_H(s))}}=t-t_0)
|
|
 |
sterni17
Anmeldungsdatum: 17.10.2022
Beiträge: 3
|
 sterni17 Verfasst am: 19. Okt 2022 10:58 Titel: sterni17 Verfasst am: 19. Okt 2022 10:58 Titel: |
 |
|
Hey, vielen Dank für eure Antworten.
s ist in dem System jetzt ja der Federweg. Müsste ich Wh nicht von h abhängig machen? Sprich:
 = F_h \cdot h = F_h \cdot \sqrt{L^2 -lf^2} )
Viele Grüße
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 19. Okt 2022 13:03 Titel: Mathefix Verfasst am: 19. Okt 2022 13:03 Titel: |
 |
|
| sterni17 hat Folgendes geschrieben: | Hey, vielen Dank für eure Antworten.
s ist in dem System jetzt ja der Federweg. Müsste ich Wh nicht von h abhängig machen? Sprich:
 = F_h \cdot h = F_h \cdot \sqrt{L^2 -lf^2} )
Viele Grüße |
 = m \cdot g \cdot h(s) )
 = \sqrt{L^{2} - (L-s)^{2} } )
 = m \cdot g \cdot \sqrt{2\cdot L\cdot s - s^{2}} )
|
|
 |
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 851
|
 Qubit Verfasst am: 19. Okt 2022 16:46 Titel: Qubit Verfasst am: 19. Okt 2022 16:46 Titel: |
 |
|
Ich würde hier - wie von Myon vorgeschlagen - gleich über den Energiesatz gehen..
Mit s: Federlänge, also  : :
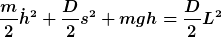
^2 - \frac{D}{2} h(t)^2 + mgh(t) = 0)
Nach der Zeit t ableiten:
 - \frac{D}{m} h(t) + g ] \cdot \dot h(t) = 0)
[..] liefert die entsprechende DGL mit den Lösungen:
 = \frac{m g}{D})
 = c_1 e^{\sqrt{\frac{D}{m}} t} + c_2 e^{-\sqrt{\frac{D}{m}} t})
 = h_H(t) + h_P(t))
Die Kraft ist dann:
 = m \cdot \ddot h(t) = D \cdot h_H(t) = D [h(t) - h_P(t)] = D \cdot h(t) - mg)
PS: man muss bei den Integrationskonstanten beachten, dass D*h > m*g
|
|
 |
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 851
|
 Qubit Verfasst am: 19. Okt 2022 20:37 Titel: Qubit Verfasst am: 19. Okt 2022 20:37 Titel: |
 |
|
Wenn man jetzt deine Gesamtkonstruktion betrachtet, sollte folgendes gelten..
- pro Komponente gibt es 2 Federn, also doppelte Kraft.
- mit den Komponenten addieren sich die Kräfte, d.h. de facto sind die Federn parallel und die Federkonstanten addieren sich mit den n Komponenten:
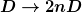
Der Hub ist pro Komponente 2*h, also bedeutet das für die abgeleitete Lösung:
 \rightarrow \frac{h(t)}{2n})
Mithin ergibt sich als Lösung für deine Konstruktion mit n Komponenten:
 = 2n [c_1 e^{\sqrt{\frac{2nD}{m}} \cdot t} + c_2 e^{-\sqrt{\frac{2nD}{m}} \cdot t} + \frac{m g}{2nD}])
Mit der Geamtkraft für n Komponenten:
 = 2nD \cdot h(t) - mg)
|
|
 |
|
















