| Autor |
Nachricht |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 06. März 2007 11:10 Titel: Bewegungsgleichung aufstellen - Taylor-Approximation Incognito Verfasst am: 06. März 2007 11:10 Titel: Bewegungsgleichung aufstellen - Taylor-Approximation |
 |
|
kann mir jemand bei der folgenden aufgabe helfen? habe leider keine richtige idee wie ich anfangen sollte. dgl's haben wir in analysis auch erst angefangen..
und ich hab auch noch nicht so ganz rausgefunden wann ich die taylor entwicklung anwenden kann. also das würd mich ganz allgemein interessieren - unser übungsleiter meinte immer wenn in der aufgabe steht "a ist sehr viel kleiner als b" wär nett wenn das jemand mal präzisieren könnte.
vielen dank im vorraus!
inco
| Beschreibung: |
|

Download |
| Dateiname: |
physik-serie_federn001.jpg |
| Dateigröße: |
65.07 KB |
| Heruntergeladen: |
2733 mal |
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 06. März 2007 12:15 Titel: dermarkus Verfasst am: 06. März 2007 12:15 Titel: |
 |
|
Bei einer Taylor-Approximation erster Ordnung einer Funktion f(x) in der Nähe der Stelle x_0 nähert man die Funktion f(x) an, indem man sie durch die Tangente an diese Funktion im Punkt x_0 ersetzt.
Wenn die Funktion eine irgendwie gekrümmte Funktion ist, dann ist natürlich diese Näherung um so besser, je näher man sich an x_0 befindet.
In dem zweidimensionalen Fall in dieser Aufgabe machst du das ganze für zwei Dimensionen, das heißt, du näherst eine gekrümmte Fläche durch eine Tangentialebene an.
-------------------------
Weißt du denn schon, was eine Bewegungsgleichung ist und wie man sie aufstellt? Wie lautete der a)-Teil und deine Lösung dazu? (ich vermute, was du da gelernt hast, kannst du in b) weiterverwenden.)
Wie sieht das ganze aus, wenn du damit mal mutig anfängst, die Bewegungsgleichung aufzustellen und hinzuschreiben?
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 06. März 2007 12:28 Titel: Incognito Verfasst am: 06. März 2007 12:28 Titel: |
 |
|
joa das war mir auch schon klar, wir hatten nur mal ne übungsaufgabe wo wir nur einen teil der gleichung entwickeln sollten und es konnte mir irgendwie keiner sagen warum.. naja müsste ich dann wohl speziell zu der aufgabe ne frage stellen.
aber kann mir noch jemand nen tipp geben zu dieser?
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 06. März 2007 13:19 Titel: Incognito Verfasst am: 06. März 2007 13:19 Titel: |
 |
|
oh da stand ja noch was, dachte das wäre die signatur 
im teil a) war ein gewicht an zwei federn (nebeneinander) aufgehängt und gefragt welche federkonstante eine feder hätte die die zwei federn ersetzt. naja k_neu = m*g/2x ?
weiß leider nicht so richtig wie ich anfangen soll
ich hab die kraft in x richtung F_x1 = -k1*x = m*x(zweimal abgeleitet) (t), analog für y
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 06. März 2007 13:57 Titel: dermarkus Verfasst am: 06. März 2007 13:57 Titel: |
 |
|
|
Welchen Ausdruck bekommst du denn, wenn du den vollen Ansatz machst und alle vier Federkräfte vektoriell addierst?
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 06. März 2007 14:24 Titel: Incognito Verfasst am: 06. März 2007 14:24 Titel: |
 |
|
F_x = -(k1+k2+k3+k4)x
F_y = -(...) y
als tipp haben wir bekommen dass F_y1,y3 und F_x2,x4 = 0 - warum das?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 06. März 2007 18:00 Titel: dermarkus Verfasst am: 06. März 2007 18:00 Titel: |
 |
|
| Incognito hat Folgendes geschrieben: | F_x = -(k1+k2+k3+k4)x
F_y = -(...) y
|
Da musst du dich beim Rechnen mit Vektoren verrechnet haben. Da hast du einfach nur x und y geschrieben, ohne dabei die verschiedenen Richtungen und die verschiedenen Auslenkungen der Federn zu berücksichtigen.
Was bekommst du denn, wenn du den vollen Ausdruck
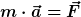
mit 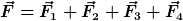
zum Rechnen verwendest?
| Incognito hat Folgendes geschrieben: |
als tipp haben wir bekommen dass F_y1,y3 und F_x2,x4 = 0 - warum das? |
Das weiß ich noch nicht, dazu müsste man erstmal loslegen mit der Rechnung. Wo stand der Tipp und wie war er genau formuliert? Soll das ein Zwischenergebnis zur Kontrolle sein oder eine Ergänzung der Aufgabenstellung in Form einer zusätzlichen Vereinfachung der Anfangsbedingungen, um die Aufgabe für euch einfacher zu machen?
Zuletzt bearbeitet von dermarkus am 07. März 2007 11:20, insgesamt einmal bearbeitet |
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 07. März 2007 10:13 Titel: Incognito Verfasst am: 07. März 2007 10:13 Titel: |
 |
|
der tipp gehört nicht zur aufgabenstellung, könnte zur überprüfung da sein. wir haben noch nen tipp bekommen der mich mehr verwirrt als dass er hilft, nämlich für k1 (nehme ich mal an):
^2+y^2}*cos(\alpha)-L)
^2+y^2}*sin(\alpha))
warum wird hier nur in x richtung ausgelenkt?
wenn ich das so nehme ist ^2+y^2}*cos(\alpha)-L)-k2*...) ? ?
sorry ich steh aufm schlauch..
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. März 2007 11:29 Titel: dermarkus Verfasst am: 07. März 2007 11:29 Titel: |
 |
|
Klammere dich erst einmal nicht zu sehr an die Tipps, die du da bekommen zu haben scheinst, sondern fang erst einmal selbst an zu rechnen. Also ganz sorgfältig Schritt für Schritt:
1) Wo liegt der Anfangspunkt der Feder 1, und welche Koordinaten hat er?
2) Wo liegt der Endpunkt der Feder 1, und welche Koordinaten hat er?
3) Wie lang ist also die Feder 1? (Tipp: Erinnere dich daran, dass du das mit dem Satz des Pythagoras ausrechnen kannst.)
4) Wie groß ist die Länge der Feder 1, wenn diese Feder im entspannten Zustand ist? Macht die Aufgabenstellung dazu eine Aussage? (Wenn ich mit dem, was ich bisher weiß, raten müsste, dann würde ich entweder annehmen, diese Länge sei Null, oder aber annehmen, diese Länge sei L)
5) Wie groß ist also die Auslenkung der Feder 1?
6) Wie groß ist also der Betrag der Federkraft 1 ?
7) In welche Richtung zeigt die Federkraft 1? Wie groß sind ihre x-Komponente und ihre y-Komponente? Kannst du dir dafür eine Skizze machen mit einem rechtwinkligen Dreieck, an dem du ablesen kannst, wie du den Winkel und die Winkelfunktionen zur Bestimmung des Ausdrucks für diese Kraftkomponenten wählen musst?
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 07. März 2007 11:58 Titel: Incognito Verfasst am: 07. März 2007 11:58 Titel: |
 |
|
joa diese tipps sind irgendwie mehr fluch als segen glaub ich :p
ok mal schaun:
1) (-L,0)
2) (L+x,y)
3) ^2+y^2}) (jetzt mach das sogar sinn *g*) (jetzt mach das sogar sinn *g*)
4) zu der aufgabe steht nicht mehr als auf diesem bild
5) in x-richtung: ^2+y^2}*cos(\alpha)-L)
in y-richtung: ^2+y^2}*sin(\alpha))
6) 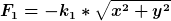 ? x,y aus 5) ? x,y aus 5)
7) ich nehe mal an sie zeigt entgegen der auslenkung
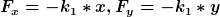 ? x,y wieder die aus 5) ? x,y wieder die aus 5)
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. März 2007 12:10 Titel: dermarkus Verfasst am: 07. März 2007 12:10 Titel: |
 |
|
| Incognito hat Folgendes geschrieben: |
1) (-L,0)
2) (L+x,y)
3) ^2+y^2}) (jetzt mach das sogar sinn *g*) (jetzt mach das sogar sinn *g*)
4) zu der aufgabe steht nicht mehr als auf diesem bild
|
So weit bin ich noch einverstanden. Damit du aber nun selbst weiterrechnen kannst, musst du für 4.) sagen, mit welcher Annahme du weiterrechnest. Denn das brauchst du dann ja in der 5), denn für die Auslenkung der Feder brauchst du erstmal gar keine x- und y-Komponente, sondern die Auslenkung der Feder ist schlicht und einfach die Differenz zwischen der aktuellen Länge der Feder (Wink mit dem Zaunpfahl: Die hast du in 3.) ausgerechnet) und ihrer Länge im entspannten Zustand.
| Zitat: |
5) in x-richtung: ^2+y^2}*cos(\alpha)-L)
in y-richtung: ^2+y^2}*sin(\alpha))
6) 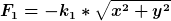 ? x,y aus 5) ? x,y aus 5)
7) ich nehe mal an sie zeigt entgegen der auslenkung
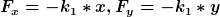 ? x,y wieder die aus 5) ? x,y wieder die aus 5) |
Da hast du dich irgendwie total verzettelt, mach das lieber nochmal sorgfältig neu, ohne dich dabei an irgendwelchen scheinbar fertigen Zwischenergebnissen aus irgendwelchen Tipps zu orientieren.
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 07. März 2007 12:29 Titel: Incognito Verfasst am: 07. März 2007 12:29 Titel: |
 |
|
ok ich nehme mal an dass alle federn im ursprung entspannt sind
ist dann die auslenkung nicht einfach ^2+y^2}-L) ? ja ok ich schmeiß die tipps glaub echt weg.. ? ja ok ich schmeiß die tipps glaub echt weg..
^2+y^2}-L))
dann ist die kraft in x richtung ^2+y^2}-L)*cos(\alpha)) ? in y eben sinus ? in y eben sinus
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. März 2007 12:37 Titel: dermarkus Verfasst am: 07. März 2007 12:37 Titel: |
 |
|
Einverstanden 
Kannst du nun noch das ) und das und das ) durch Ausdrücke ersetzen, in denen nur noch x, y und L stehen? durch Ausdrücke ersetzen, in denen nur noch x, y und L stehen?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. März 2007 12:54 Titel: dermarkus Verfasst am: 07. März 2007 12:54 Titel: |
 |
|
Nachtrag:
| Incognito hat Folgendes geschrieben: |
2) (L+x,y)
3) ^2+y^2}) (jetzt mach das sogar sinn *g*) (jetzt mach das sogar sinn *g*)
|
In 2) hast du dich übrigens noch vertippt: das Ende der Feder 1 liegt bei (x,y), denn der Koordinatenursprung liegt ja in der Mitte des Bildes.
In 3) hast du aber offenbar wieder ohne diesen Tippfehler weitergerechnet  , also stimmte es ab 3) wieder , also stimmte es ab 3) wieder 
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 07. März 2007 13:20 Titel: Incognito Verfasst am: 07. März 2007 13:20 Titel: |
 |
|
joa stimmt
meinst du mit anderer darstellung kosinus bzw sinussatz?
dann wäre das für cosinus: ^2+y^2}-L)^2-y}{2*x*(\sqrt{(L+x)^2+y^2}-L)}) ? ist das wirklich nötig? weil in den tipps (ja die bösen tipps :p) steht ein ansatz mit sinus und cosinus. ? ist das wirklich nötig? weil in den tipps (ja die bösen tipps :p) steht ein ansatz mit sinus und cosinus.
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. März 2007 13:30 Titel: dermarkus Verfasst am: 07. März 2007 13:30 Titel: |
 |
|
| Incognito hat Folgendes geschrieben: |
meinst du mit anderer darstellung kosinus bzw sinussatz?
|
Nein, einfach nur Cosinus gleich Ankathete durch Hypothenuse und Sinus gleich Gegenkathete durch Hypothenuse.
Das alpha in deinen Gleichungen musst du noch rausschmeißen, weil du ja hinterher die Gesamtkraft als Funktion von x und y haben möchtest, nicht als Funktion von alpha.
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 07. März 2007 13:53 Titel: Incognito Verfasst am: 07. März 2007 13:53 Titel: |
 |
|
hmm dann kürzt sich doch dann alles wieder raus
^2+y^2}-L)*\frac{x}{\sqrt{(L+x)^2+y^2}-L})
ich weiß ich stell mich grad ziemlich blöd an..
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 07. März 2007 17:13 Titel: dermarkus Verfasst am: 07. März 2007 17:13 Titel: |
 |
|
Tipp: Mach dir dafür unbedingt eine übersichtliche Skizze.
Sowohl bei der Ankathete (die ist nicht x, sondern länger) als auch bei der Hypothenuse (die ist nicht gleich der Auslenkung der Feder, sondern gleich der Federlänge), hast du einfache, vermeidbare Fehler gemacht, die dir nicht passiert wären, wenn du das mit sorgfältig in einer Skizze aufgemalt und abgelesen hättest.
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 08. März 2007 14:17 Titel: Incognito Verfasst am: 08. März 2007 14:17 Titel: |
 |
|
stimmts jetzt so?
^2+y^2}-L)(x+L)}{\sqrt{(L+x)^2+y^2}}+k_2*\frac{(\sqrt{x^2+(L+y)^2}-L)*x}{\sqrt{x^2+(L+y)^2}}+k_3*\frac{(\sqrt{(L-x)^2+y^2}-L)*(L-x)}{\sqrt{(L-x)^2+y^2}}+k_4*\frac{(\sqrt{x^2+(L-y)^2}-L)*x}{\sqrt{x^2+(L-y)^2}}))
das sieht unangenehm aus 
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 08. März 2007 18:20 Titel: dermarkus Verfasst am: 08. März 2007 18:20 Titel: |
 |
|
| Incognito hat Folgendes geschrieben: | stimmts jetzt so?
|
Einverstanden, da habe ich nun keinen Fehler mehr drin gefunden 
| Zitat: |
das sieht unangenehm aus  |
Einverstanden  Das ist auch genau der Grund, warum man jetzt eine Taylorentwicklung macht, um weiterrechnen zu können. Besonders für die Summanden, in denen sich die Wurzeln nicht rauskürzen. Das ist auch genau der Grund, warum man jetzt eine Taylorentwicklung macht, um weiterrechnen zu können. Besonders für die Summanden, in denen sich die Wurzeln nicht rauskürzen.
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 09. März 2007 08:40 Titel: Incognito Verfasst am: 09. März 2007 08:40 Titel: |
 |
|
wobei ich mir ableiten jetzt auch nicht so angenehm vorstelle..
also wie funktioniert das hier jetzt genau:
auf dem zettel steht: F(x,y) = F(x_0,y_0) + ... <- also für x und y dann x_0 und y_0 einsetzen? dadurch wirds doch auch nicht einfacher und die ableitung sieht in maple auch nicht gerade freundlich aus. oder versteh ich da grad was falsch?
dank dir erstmal für die ausdauer!  was bedeutet eigentlich "linearisierte bewegungsgleichung"? was bedeutet eigentlich "linearisierte bewegungsgleichung"?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. März 2007 21:40 Titel: dermarkus Verfasst am: 09. März 2007 21:40 Titel: |
 |
|
| Incognito hat Folgendes geschrieben: |
also wie funktioniert das hier jetzt genau:
auf dem zettel steht: F(x,y) = F(x_0,y_0) + ... <- also für x und y dann x_0 und y_0 einsetzen?
|
Ja, aber das ist ja nur der erste Term in dem Hinweis. Für die anderen Terme brauchst du noch die Ableitungen an der Stelle (x_0, y_0).
Jetzt musst du also genau das ausrechnen, was in dem Hinweis angegeben ist. Fang dazu beim Ableiten ruhig mit wenigen Termen an, um herauszufinden, wie man das rechnet (zum Beispiel mit Termen wie "1 geteilt durch die Wurzel"), und mach das lieber erstmal von Hand als mit Maple, dann musst du nicht zwei Sachen gleichzeitig lernen (Wie man das rechnet und wie man das in Maple eingibt).
| Zitat: |
was bedeutet eigentlich "linearisierte bewegungsgleichung"? |
Das bekommst du als Zwischenergebnis, wenn du die Taylorapproximation geschafft hast 
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 09. März 2007 22:47 Titel: Incognito Verfasst am: 09. März 2007 22:47 Titel: |
 |
|
[quote="dermarkus"] | Incognito hat Folgendes geschrieben: |
Das bekommst du als Zwischenergebnis, wenn du die Taylorapproximation geschafft hast  |
das dacht ich mir fast  ich meinte was bedeutet linear in diesem fall? linear in den anfangsbedingungen? ich meinte was bedeutet linear in diesem fall? linear in den anfangsbedingungen?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. März 2007 22:48 Titel: dermarkus Verfasst am: 09. März 2007 22:48 Titel: |
 |
|
|
Ich denke, linear in (x-x_0) und (y-y_0). Aber das siehst du besser, wenn du die Taylorapproximation wie angegeben ausgerechnet hast.
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 09. März 2007 23:25 Titel: Incognito Verfasst am: 09. März 2007 23:25 Titel: |
 |
|
ich bezweifle zwar fast dass das richtig ist aber mal schaun was du dazu sagst:
für die ableitung des ersten terms hab ich: ^2+y_0^2}}{(L+x_0)^2+y_0^2}+\frac{x_0*L*(2L+2x_0)}{2*((L+x_0)^2+y_0^2)^(3/2)}+\frac{L^2*(2L+2x_0)}{2*((L+x_0)^2+y_0^2)^(3/2)}))
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. März 2007 00:20 Titel: dermarkus Verfasst am: 10. März 2007 00:20 Titel: |
 |
|
Magst du daraus noch eine Gleichung machen, indem du dazuschreibst, dass das die partielle Ableitung der x-Komponente der Kraft F_1 nach x_0 und y_0 sein soll,
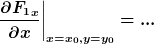
und magst du vor allem dein Ergebnis noch vereinfachen, indem du die Brüche addierst? Dann lässt sich das besser vergleichen. Mein Ergebnis sieht, wenn es fertig vereinfacht ist, deutlich kürzer aus.
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 10. März 2007 09:47 Titel: Incognito Verfasst am: 10. März 2007 09:47 Titel: |
 |
|
^{\frac{3}{2}}}+1))
wer hat sich nur so ne scheiß aufgabe einfallen lassen..
\\Anm. d. Red. : x^{\frac{3}{2}} oder x^{3/2} (Nikolas)
danke
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. März 2007 14:21 Titel: dermarkus Verfasst am: 10. März 2007 14:21 Titel: |
 |
|
Da bekomme ich ein anderes Ergebnis: Mein Ergebnis unterscheidet sich von deinem dadurch, dass sich bei mir im Zähler des Bruches alle Terme mit 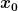 herausheben, und dass der Term mit herausheben, und dass der Term mit 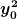 anders aussieht als bei dir. anders aussieht als bei dir.
Magst du deine Ableitung nochmal sauber neu rechnen? Das ist nichts anderes als sorgfältig ableiten und sorgfältig umformen, und um Rechenfehler bei längeren Rechnungen oder beim Rechnen mit größeren Termen zu vermeiden, hilft vielen der Tipp, die Rechnung beim Rechnen möglichst sauber aufzuschreiben.
Magst du, falls du dir dann trotz sorgfältigem Rechnen noch nicht sicher bist, mal deine Rechnung mit allen Zwischenschritten, die du gemacht hast, hier aufschreiben, so dass wir sehen können, wo es dann noch hakt?
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 10. März 2007 16:06 Titel: Incognito Verfasst am: 10. März 2007 16:06 Titel: |
 |
|
oh mann einmal x und L vertauscht >.<
hab jetzt: ^2+y_0^2)^{3/2}}+1)
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 10. März 2007 18:31 Titel: dermarkus Verfasst am: 10. März 2007 18:31 Titel: |
 |
|
Rechts oben im Zähler meinst du sicher y_0 statt y, und das -k_1 vornedran hast du sicher einfach nur vergessen..
Und könnte es sein, dass wenn du nochmal kontrollierst, dass sich bei dir der erste Term im Zähler noch "verflüchtigt" ? In meinem Ergebnis habe ich den nicht bekommen.
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 12. März 2007 09:10 Titel: Incognito Verfasst am: 12. März 2007 09:10 Titel: |
 |
|
hm das x_0*L^2 verschwindet bei mir nicht aber ich nehm mal dein ergebnis, hab irgendwie nicht so viel lust jetzt mich jetzt ewig mit so nem kleinkram rumzuschlagen..
was mach ich denn wenn ich das alles hab? (ich glaub die aufgabe ist echt nur um arme studenten zu quälen..)
ich hab hier den ansatz =A*sin(\omega_x*t)+B*cos(\omega_x*t)) dasselbe für sinus (C und D statt A,B)und zusätzlich die beiden (vermute ich mal) ergebnisse: dasselbe für sinus (C und D statt A,B)und zusätzlich die beiden (vermute ich mal) ergebnisse: *x) und und *y)
wie genau erhalte ich damit A,B,C,D? normal würde ich ja sagen den ansatz zweimal ableiten und für x'' bzw y'' einsetzen und die omegas durch x_0/y_0 ersetzen. aber was mach ich dann mit den anfangsgeschwindigkeiten?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 12. März 2007 12:47 Titel: dermarkus Verfasst am: 12. März 2007 12:47 Titel: |
 |
|
| Incognito hat Folgendes geschrieben: | hm das x_0*L^2 verschwindet bei mir nicht aber ich nehm mal dein ergebnis, hab irgendwie nicht so viel lust jetzt mich jetzt ewig mit so nem kleinkram rumzuschlagen..
|
Hm, studierst du Physik? Ein Indianer, der auf den Stuhl springt, wenn er eine Maus sieht, ist ein bisschen komisch. So ein bisschen ähnlich kommt mir das vor, wenn man als Physikstudent kneift, wenn es ums Ableiten und Umformen geht.
Magst du deine Rechnung für die Ableitung von oben, das sind sicher nicht mehr als ca. 3 bis 7 Zeilen Rechnung, je nachdem wie ausführlich du deine Zwischenschritte machst, hier sauber aufschreiben; dann haben wir im Nu herausgefunden, woran es liegt 
| Zitat: |
was mach ich denn wenn ich das alles hab? |
Dann kannst du das ganze sehr übersichtlich schreiben, indem du genau hinschaust, was Konstanten sind und was du am besten als Variablen verwendest, und welche Konstanten du zusammenfassen und mit abkürzenden Bezeichnungen versehen kannst, und dann machst du dich daran, die Bewegungsgleichung mit diesen Konstanten und Variablen zu lösen.
(Dein Versuch, einen Zwischenteil der Aufgabe durch Raten zu überspringen, war danebengeraten.)
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 12. März 2007 14:12 Titel: Incognito Verfasst am: 12. März 2007 14:12 Titel: |
 |
|
ja ich wollte ein bisschen abkürzen weil es doch sehr mühsam ist zwei so riesen funktionen jeweils zweimal abzuleiten, angst ist das falsche wort.
nungut wie du willst ich schreibs mal auf.
*-k_1*(\frac{x*\sqrt{(L+x)^2+y^2}-x*L+L*\sqrt{...}-L^2}{\sqrt{...}})) ... ist das unter der wurzel, das is ja eh immer gleich ... ist das unter der wurzel, das is ja eh immer gleich
}{2\sqrt{...}}-L+\frac{L*(2L+2x)}{2\sqrt{...}})*\sqrt{...}-(x*\sqrt{...}-x*L+L\sqrt{...}-L^2)*\frac{(2L+2x)}{2\sqrt{...}})*\frac{1}{\sqrt{...}^2})) nicht über \sqrt{...}^2 wundern, das hab ich nur grad im speicher nicht über \sqrt{...}^2 wundern, das hab ich nur grad im speicher 
^2+y^2+\frac{1}{2}x(2L+2x)-L*\sqrt{...}+\frac{1}{2}L*(2L+2x)-(1/2)x(2L+2x)+\frac{x*L(2L+2x)}{2*\sqrt{...}}-(1/2)L(2L+2x)+\frac{L^2(2L+2x)}{2*\sqrt{...}})*\frac{1}{\sqrt{...}^2})) genau deswegen hat ich keine lust das aufzuschreiben :p genau deswegen hat ich keine lust das aufzuschreiben :p
(2L+2x)(2L+2x)}{2*\sqrt{...}^{3/2}}))
(xL+L^2)-2L(L^2+2Lx+x^2+y^2)}{2*\sqrt{...}^{3/2}}+1)) ausklammern kürzen etc.. ausklammern kürzen etc..
Zuletzt bearbeitet von Incognito am 12. März 2007 14:33, insgesamt einmal bearbeitet |
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 12. März 2007 14:16 Titel: Incognito Verfasst am: 12. März 2007 14:16 Titel: |
 |
|
|
so und das noch für die drei anderen k's und das gleiche nochmal nach y und dann noch für die kräfte in y-richtung nochmal... verstehst nicht warum ich das bissl abkürzen will? das ist reine schinderei und am ende bin ich immer noch nicht schlauer wie das jetzt mit dem ansatz funktioniert..
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 12. März 2007 17:39 Titel: dermarkus Verfasst am: 12. März 2007 17:39 Titel: |
 |
|
| Incognito hat Folgendes geschrieben: | (...) so riesen funktionen (...)
*-k_1*(\frac{x*\sqrt{(L+x)^2+y^2}-x*L+L*\sqrt{...}-L^2}{\sqrt{...}})) ... ist das unter der wurzel, das is ja eh immer gleich ... ist das unter der wurzel, das is ja eh immer gleich
|
Jetzt verstehe ich, wo das Problem ist !
Ich verrate dir mal ein großes Geheimnis: Unbedingt immer erst vereinfachen, und dann erst weiterrechnen !!
Für die Funktion ) (also die x-Komponente der Kraft (also die x-Komponente der Kraft 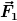 ) bekomme ich, wenn ich ich vor dem Weiterrechnen vereinfache, einen viel einfacheren Ausdruck, vor allem die Wurzeln solltest du unbedingt erstmal rauskürzen, bevor du mit dem Ableiten loslegst: ) bekomme ich, wenn ich ich vor dem Weiterrechnen vereinfache, einen viel einfacheren Ausdruck, vor allem die Wurzeln solltest du unbedingt erstmal rauskürzen, bevor du mit dem Ableiten loslegst:
 = -k_1\left(x+L-\frac{L(x+L)}{\sqrt{(x+L)^2+y^2}} \right))
Und damit rechnet es sich doch gleich schon viel einfacher weiter, findest du nicht auch?
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 12. März 2007 18:31 Titel: Incognito Verfasst am: 12. März 2007 18:31 Titel: |
 |
|
ich fürchte du hast recht, das ist wirklich angenehmer  nun gut dann mach ichs wohl doch mal noch für alle und dann sehn wir weiter nun gut dann mach ichs wohl doch mal noch für alle und dann sehn wir weiter 
aber wo ist jetzt der fehler in meiner rechnung? *grml*
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 13. März 2007 00:55 Titel: dermarkus Verfasst am: 13. März 2007 00:55 Titel: |
 |
|
| Incognito hat Folgendes geschrieben: |
aber wo ist jetzt der fehler in meiner rechnung? *grml*
|
In deiner Rechnung von der ersten zur fünften Zeile finde ich zwar Schreibfehler, aber keine Rechenfehler 
In der vierten Zeile ist im Term
| Incognito hat Folgendes geschrieben: |
(2L+2x)(2L+2x)}{2*\sqrt{...}^{3/2}}))
|
ein Faktor (2L+2x) zu viel im Zähler, (in der vierten Zeile stimmt das allerdings wieder, also war das sicher nur ein Eintippfehler)
und statt 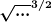 meinst du sicher immer jeweils meinst du sicher immer jeweils 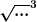 . .
Mit deinem Zwischenergebnis in der letzten Zeile
| Zitat: |
(xL+L^2)-2L(L^2+2Lx+x^2+y^2)}{2*\sqrt{...}^{3/2}}+1)) ausklammern kürzen etc.. ausklammern kürzen etc.. |
bin ich einverstanden (denn im Nenner meinst du sicher "hoch 3" statt "hoch 3/2"); dein Rechenfehler muss also irgendwo danach im Ausklammern und Kürzen liegen 
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 13. März 2007 12:18 Titel: Incognito Verfasst am: 13. März 2007 12:18 Titel: |
 |
|
so jetzt kommen wir der sache näher:
}{\partial x}=-k_1*(1-\frac{Ly^2}{((L+x)^2+y^2)^{3/2}}))
}{\partial x}=-k_2*(1-\frac{L(L+y)^2}{(x^2+(L+y)^2)^{3/2}}))
}{\partial x}=-k_3*(-(1-\frac{Ly^2}{((L-x^2)+y^2)^{3/2}}))
}{\partial x}=-k_4*(1-\frac{L(L-y)^2}{(x^2+(L-y^2)^{3/2}}))
}{\partial y}=-k_1*(-\frac{Lxy+L^2y}{\sqrt{(x+L)^2+y^2}}))
}{\partial y}=-k_2*(-\frac{Lxy+L^2x}{\sqrt{x^2+(L+y)^2}}))
}{\partial y}=-k_3*(\frac{Lxy+L^2y}{\sqrt{(L-x)^2+y^2}}))
}{\partial y}=-k_4*(-\frac{Lxy-L^2x}{\sqrt{x^2+(L-y)^2}}))
hoffe es stimmt jetzt wenigstens modulo tippfehler
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 13. März 2007 13:17 Titel: dermarkus Verfasst am: 13. März 2007 13:17 Titel: |
 |
|
Da bin ich schon mit fast allem einverstanden 
Nur in den Ableitungen von F_x3 und F_x4 nach x ist die Klammersetzung im Ergebnis noch falsch (besonders im Nenner beim Quadrat),
und dein Ergebnis für die Ableitung von F_x4 nach y enthält einen Vorzeichenfehler.
Kannst du damit nun die linearisierte Bewegungungsgleichung für die x-Komponente der Gesamtkraft komplett hinschreiben?
|
|
 |
Incognito
Anmeldungsdatum: 24.02.2007
Beiträge: 23
|
 Incognito Verfasst am: 14. März 2007 15:16 Titel: Incognito Verfasst am: 14. März 2007 15:16 Titel: |
 |
|
ja hab aber alles richtig aufm zettel geschrieben nur falsch abgetippt..
die bewegungsgleichung aufstellen ist ja nur alles zusammenpacken wies auf dem zettel steht, aber kann es sein dass das ergebnis immer noch recht unangenehm ist? kann sein dass ich wieder den überblick verloren habe aber irgendwie kürzt sich da diesmal gar nichts raus wenn ich z.b. alle k_1 therme zusammenfasse?
|
|
 |
|



















 nun gut dann mach ichs wohl doch mal noch für alle und dann sehn wir weiter
nun gut dann mach ichs wohl doch mal noch für alle und dann sehn wir weiter