| Autor |
Nachricht |
Ula
Gast
|
 Ula Verfasst am: 07. Mai 2014 20:06 Titel: Bewegungsgleichung, Kegelgleichung |
 |
|
Meine Frage:
Ein Massenpunkt der Masse m gleitet reibungsfrei auf einem Kegelmantel, dessen Achse parallel zum Schwerefeld steht. Die Kegelgleichung sei
dabei \sqrt{x²+y²} =z\cdot tan\alpha
mit z, \alpha > 0.
(a) Geben Sie die Lagrange-Funktion in den Koordinaten z und \varphi =arctan(y/x) an.
(b) Stellen Sie die Lagrange-Bewegungsgleichungen auf.
(c) Zeigen Sie, dass für den Fall z(t)=z_{0} die Gleichungen aus (b) eine horizontale
Kreisbahn mit konstanter Winkelgeschwindigkeit \omega beschreiben
und geben Sie diese Winkelgeschwindigkeit an.
(d) Geben Sie die Zwangskraft des Kegels auf den Massenpunkt für den Spezialfall aus (c) an.
Meine Ideen:
ALso ich habe schon überlegt, ob ich mit Polarkoordinaten arbeiten soll, oder mit den trigonometrischen Funktionen. Dann wäre z.B. y=x tan \phi; z=x/tan(\alpha) Aber ich weiß nicht, ob das so ok wäre. |
|
 |
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 07. Mai 2014 21:44 Titel: |
|
|
Verstehe nicht die Frage: Es steht doch da, welche beiden Variablen Du nehmen sollst: z und 
Wie ist denn T und V in Abhängigkeit dieser beiden Variablen, wenn sich die Masse immer auf dem Kegelmantel befindet?
Gruß
Marco |
|
|
ula
Gast
|
| ula Verfasst am: 08. Mai 2014 11:46 Titel: |
|
|
|
ALso T=0,5 m T= 0,5 m v² = 0,5 (\dot{x} ² + \dot{y} ² + \dot{z} ²) |
|
|
Ula
Gast
|
| Ula Verfasst am: 08. Mai 2014 11:49 Titel: |
|
|
|
Nur wie soll ich x und y als z und phi schreiben? |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 08. Mai 2014 13:26 Titel: |
|
|
Hallo,
ich denke am einfachsten ist es, wenn Du Dir das hier überlegst:
Die Masse ist an einem bestimmten Punkt auf dem Kegelmantel mit einem bestimmten z und einem bestimmten phi. Wenn Du das phi um  veränderst, wie weit bewegt sich dann die Masse?
Wenn Du z um dz veränderst, dann ändert sich ja nicht nur z, sondern die Masse muss sich schräg entlang des Kegelmantels bewegen. Um wieviel?
Diese beiden Bewegungsrichtungen, also in phi-Richtung und entlang der Schrägen des Kegelmantels nach oben und unten, stehen senkrecht aufeinander, so dass Du mit dem Pythagoras das gesamt ds ausrechnen kannst.
Gruß
Marco |
|
|
Ula
Gast
|
| Ula Verfasst am: 08. Mai 2014 20:31 Titel: |
|
|
"Diese beiden Bewegungsrichtungen, also in phi-Richtung und entlang der Schrägen des Kegelmantels nach oben und unten, stehen senkrecht aufeinander, so dass Du mit dem Pythagoras das gesamt ds ausrechnen kannst. "
Warum stehen sie senkrecht aufeinander? Ich würde sagen, dass der Winkel (90° - alfa) ist... |
|
|
Ula
Gast
|
| Ula Verfasst am: 08. Mai 2014 21:44 Titel: |
|
|
Also ich danke, das müsste ungefähr so sein:
 + ............)) |
|
|
Ula
Gast
|
| Ula Verfasst am: 09. Mai 2014 12:44 Titel: |
|
|
|
Also T= 0, 5 m (... ) natürlich |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 09. Mai 2014 13:32 Titel: |
|
|
| Ula hat Folgendes geschrieben: | | Warum stehen sie senkrecht aufeinander? Ich würde sagen, dass der Winkel (90° - alfa) ist... |
Ein Einheitsvektor in Richtung phi ist doch parallel zur x-y-Ebene und tangential. Der in Richtung schräg oben/unten hat nur einen radialen Anteil (also von der Achse weg oder hin) und einen nach oben/unten.
ME müsste also das hier sein:
^2 = \left[\frac{1}{\cos{\alpha}}\cdot\mathrm dz\right]^2 + \left[\left(z\tan{\alpha}\right)\cdot \mathrm d\phi\right]^2)
Gruß
Marco |
|
|
Ula
Gast
|
| Ula Verfasst am: 09. Mai 2014 20:40 Titel: |
|
|
Also ich habe zuerst x ausgerechnet:
 }{1+\tan²(\varphi ) } } =z \tan(\alpha ) \cos(\varphi ))
y:
 \sin(\varphi ) ) .
Da es nur eine Zwangsbed. gibt: 3*1-1=2. Ich muss 2 generalisierten Koordinaten haben. Sei nun :
Dann erhalte ich :
 \sin(q_{2} )
<br />
und
<br />
\dot{y} = -q_{1} \dot{q_{2} } ² \tan(\alpha ) \cos(q_{2} )) |
|
|
Ula
Gast
|
| Ula Verfasst am: 09. Mai 2014 20:48 Titel: |
|
|
DIe kinetische Energie:
 + \dot{q_{1}² } )) .
Die potentielle Energie:
V=mgz
DIe Lagrange Funktion:
 + \dot{q_{1}² } ] - mgz) . Ist das so OK? |
|
|
Ula
Gast
|
| Ula Verfasst am: 09. Mai 2014 21:46 Titel: |
|
|
Also wenn das richtig ist, dann habe ich in b).: Bewegungsgleichung für q1:
 + g=0)
und für q2:
 + q_{1} ² \ddot{q_{2} } \tan ²(\alpha ) =0
<br />
<br />
)
Ist das richtig so? Oder habe ich mich verrechnet?
Gruß
Ula |
|
|
Ula
Gast
|
| Ula Verfasst am: 09. Mai 2014 21:58 Titel: |
|
|
|
WIe kann ich nun die c) lösen? |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 10. Mai 2014 03:01 Titel: |
|
|
Nein...
Also erstens: Du musst nicht q1, q2 und so verwenden, Du kannst ruhig auch phi und z weiter verwenden!
Dann weiß ich nicht, was Du da mal mit einem q2² und mal ohne hast...
Dann stimmt das mit der z-Komponenten nicht: Wenn sich die Masse um eine Einheit in z-Richtung bewegt, dann ist die Strecke, die sie sich bewegt hat, größer. Letztlich stimmt dein 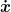 dann auch nicht, weil x und y sich automatisch verändert, wenn sich z verändert.
Du machst Dir das viel zu kompliziert: Wenn sich der Winkel verändert aber z festgehalten wird, dann bewegt sich die Masse auf einer Kreisbahn und der Radius kann direkt über  angegeben werden. Du hast also:
und außerdem:
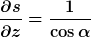
Und die beiden Bewegungsrichtung stehen senkrecht aufeinander, ob Du es glaubst oder nicht!
Dann hast Du (wie ich schon geschrieben hatte...)
^2 + \left(\frac{1}{\cos{\alpha}}\dot z\right)^2)
Dann ist nämlich der Lagrange:
^2 + \left(\frac{1}{\cos{\alpha}}\dot z\right)^2\right] - mgz)
Gruß
Marco |
|
|
Ula
Gast
|
| Ula Verfasst am: 10. Mai 2014 08:37 Titel: |
|
|
Sorry, da habe ich mich vertippt, es soll so sein, wenn ich noch z und phi benutze
 \sin(\varphi ) \\
<br />
\dot{y} = z \dot{\varphi } \tan(\alpha) \cos(\varphi ) )
Ich denke, wenn ich nur in meiner Lagrange Funktion 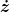 ändern werde: 1/cos alpha , dann sehen unsere Funktionen gleich aus.
Bin davon ausgegangen, dass:
, deswegen \ steht \ bei\ mir\ \dot{z} \ ohne \ \frac{1}{\cos(\alpha ) } .) |
|
|
Ula
Gast
|
| Ula Verfasst am: 10. Mai 2014 08:40 Titel: |
|
|
|
Jetzt noch die Lagrange Bewegungsgleichung.... |
|
|
Ula
Gast
|
| Ula Verfasst am: 10. Mai 2014 08:52 Titel: |
|
|
Und diese ist:
 \cdot \dot{\varphi })
 } \dot{z} )
 } \ddot{z} - mz \tan ²(\alpha ) \dot{\varphi } ²)
Ist das so ok? |
|
|
Ula
Gast
|
| Ula Verfasst am: 10. Mai 2014 09:12 Titel: |
|
|
Stimmt, meine Lösung ist wesentlich aufwändiger , aber ich dachte, wenn die Kegelgleichung vorgegeben ist und ) , dann soll man das auch nutzen. |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 10. Mai 2014 09:29 Titel: |
|
|
Zu dem z-Punkt: eigentlich stimmen Deine Gleichungen für x-Punkt und y-Punkt nicht. X hängt ja sowohl von phi als auch von z ab und es verändert sich, wen z sich verändert. Also muss doch auch in x-Punkt irgendwo ein z-Punkt vor kommen. Genau so in y-Punkt.
Dann zu der Rechnung in Deinem vorletzten Post. In der ersten Zeile fehlt ein Quadrat am Ende, ist aber offenbar nur ein Tippfehler, weil Du ja in der letzten das wieder dabei hast. In der zweiten Zeile fehlt noch der Faktor m/2. da ist doch eine Klammer davor beim Ausdruck für L, also musst Du den natürlich in jeden Summanden einmultiplizieren.
Das fällt mir gerade im Moment so auf.
Ich denke, die Angabe mit x, y und dem Tangens ist letztlich nur gemacht, um klar den Kegel und den Winkel und auch die z-Achse zu bestimmen. Es steht ja explizit dann auch da, dass man z und phi als die beiden unabhängigen Variablen verwenden solle. Wenn Du Deine Rechning richtig gemacht hättest, wärest Du ja auch aufs richtige Ergebnis gekommen.
Gruß
Marco |
|
|
Ula
Gast
|
| Ula Verfasst am: 10. Mai 2014 12:11 Titel: |
|
|
|
Ok. Eigentlixh hast du recht. Uns wurde nur ein tipp gegeben, dass wir die gegebene funktion nach x und y auflösen sollen. Deswegen weiss ich nicht wie ich auf 1/ cos alfa bei z kommen soll. |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 10. Mai 2014 16:17 Titel: |
|
|
Ich hatte doch schon geschrieben: Deine x-Punkt und y-Punkt sind falsch! Schreibe x und y in Abhängigkeit von z und phi nochmal hin. Die totale Ableitung nach der Zeit ist dann doch:
Genau so für y-Punkt.
Rechne das mal nochmal aus, das stimmt bei Dir nämlich einfach nicht, ich kann kein z-Punkt bei Dir entdecken!
Gruß
Marco |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 11. Mai 2014 00:41 Titel: |
|
|
Hallo!
Ich hab das mal nochmal für Dich gerechnet, damit Du siehst, dass das schon aufs selbe raus läuft:
Jetzt die Geschwindigkeit:
Da siehst Du, der Mischterm hebt sich weg, weil er bis auf das Vorzeichen identisch ist. Daraus ergibt sich dann:
\dot z^2 + z^2\dot{\varphi}^2\tan^2{\alpha}
<br />
&=& \frac{\cos^2{\alpha} + \sin^2{\alpha}}{\cos^2{\alpha}} \dot z^2 + z^2\dot{\varphi}^2\tan^2{\alpha}
<br />
&=&\frac{1}{\cos^2{\alpha}} \dot z ^2+ z^2\dot{\varphi}^2\tan^2{\alpha})
Kommt also genau das selbe raus... Nur dass ich das auch gleich so sagen konnte, ohne die längliche Rechnung. 
Gruß
Marco |
|
|
Ula
Gast
|
| Ula Verfasst am: 11. Mai 2014 11:39 Titel: |
|
|
OK, das überzeugt mich ! Danke!
Nun komme ich zu der Aufgabe b). (Bewegungsgleichung)
für z:
 } \dot{z} \\
<br />
\frac{\dd }{\dd x} \frac{\partial L}{\partial \dot{z} } = m \frac{1}{\cos ²(\alpha ) }\ddot{z} \\
<br />
\frac{\partial L}{\partial z} = m\dot{\varphi } ² z \tan²(\alpha ) - mg\\
<br />
\frac{\dd }{\dd x} \frac{\partial L}{\partial \dot{z} }- \frac{\partial L}{\partial z} = m \frac{1}{\cos ²(\alpha ) }\ddot{z} - m\dot{\varphi } ² z \tan²(\alpha ) - mg\\) |
|
|
Ula
Gast
|
| Ula Verfasst am: 11. Mai 2014 11:49 Titel: |
|
|
Und für phi:
\\
<br />
<br />
\frac{\dd }{\dd x} \frac{\partial L}{\partial \dot{\varphi } } =
<br />
2m\dot{\varphi } \tan ²(\alpha ) z \dot{z} +m z² \tan ²(\alpha ) \ddot{\varphi }
<br />
\\
<br />
\frac{\dd }{\dd x} \frac{\partial L}{\partial \dot{z} }- \frac{\partial L}{\partial z} = 2m\dot{\varphi } \tan ²(\alpha ) z \dot{z} +m z² \tan ²(\alpha ) \ddot{\varphi }) |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 11. Mai 2014 11:50 Titel: |
|
|
Ja.
Allerdings leitest Du nicht nach x ab (weil Du immer d/dx geschrieben hast), sondern nach t, also musst Du d/dt schreiben.
Dann ist das unten ja noch keine echte Gleichung. Da fehlt noch, dass die gerade 0 sein muss. Du musst also noch ein = 0 hinten dran schreiben.
Und jetzt noch die mit phi. Das ist eine zyklische Variable (sie kommt in L nicht vor, nur phi-Punkt), deshalb wird da wohl ein Erhaltungssatz raus kommen.
Gruß
Marco |
|
|
Ula
Gast
|
| Ula Verfasst am: 11. Mai 2014 11:54 Titel: |
|
|
Ja, natürlich nach t. (in der Formel in Latex ist immer d/dx und ich habe vergessen das zu ändern).
"=0" ist mir auch klar.
Nun brauche ich ein Tipp für die Aufgabe c) |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 11. Mai 2014 12:07 Titel: |
|
|
Hallo!
OK, das sieht alles ganz gut aus. Sehr schön! 
Die Aufgabe ist jetzt: z soll einen konstanten Wert  = z_0) haben. Logischerweise ist dann  = 0) und genau so die Beschleunigung in z auch (also die zweite Ableitung nach der Zeit).
Das kannst Du einmal in die Bewegungsgleichung einsetzen, die Du für phi bekommen hast. Alle Summanden, in denen ein  oder  vorkommt, fallen dann ja automatisch weg.
Wenn Du das tust, was bekommst Du dann für die phi-Ableitungen für Ergebnisse aus den Bewegungsgleichungen?
Gruß
Marco |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 11. Mai 2014 12:08 Titel: |
|
|
Mir ist noch was aufgefallen: Du hast das Vorzeichen am Ende vor dem mg falsch, bei der Gleichung für z. Schau das nochmal an!
Gruß
Marco |
|
|
Ula
Gast
|
| Ula Verfasst am: 11. Mai 2014 12:22 Titel: |
|
|
Ja, stimmt. Die Potentielle Energie hat "+" Vorzeichnen. --> in der L-Funktion dann "-". und weil ich in der Bewegungsgleichung substrahieren muss, dann habe ich wieder "+".
Gruß
Ula |
|
|
Ula
Gast
|
| Ula Verfasst am: 11. Mai 2014 12:25 Titel: |
|
|
c).: Ich erhalte dann:
 =0) |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 11. Mai 2014 12:45 Titel: |
|
|
Gut, dabei ist ja alles dann konstant, außer 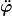 . Damit hast Du schonmal raus bekommen, dass die Winkelgeschwindigkeit konstant ist, also eine gleichförmige Kreisbewegung vorliegt.
Jetzt nimm Dir noch die andere Gleichung vor!
Gruß
Marco |
|
|
Ula
Gast
|
| Ula Verfasst am: 11. Mai 2014 12:54 Titel: |
|
|
 + mg=0 ) |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 11. Mai 2014 13:57 Titel: |
|
|
Du hast das Vorzeichen schon wieder falsch.
Dann einfach nach der Winkelgeschwindigkeit auflösen.
Gruß
Marco |
|
|
Ula
Gast
|
| Ula Verfasst am: 11. Mai 2014 14:08 Titel: |
|
|
ok, stimmt, also dann habe ich:
 } } ) .
Gruß,
Ula |
|
|
Ula
Gast
|
| Ula Verfasst am: 11. Mai 2014 14:29 Titel: |
|
|
d). Nun muss ich noch die Zwangskraft berechnen. Es gibt solche Formel:
 |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 11. Mai 2014 14:39 Titel: |
|
|
| Ula hat Folgendes geschrieben: | ok, stimmt, also dann habe ich:
|
Ich bin am grübeln... Bei mir ist kein Quadrat am phi-Punkt gewesen und dann beim Ergebnis auch keine Wurzel... 
Gruß
Marco |
|
|
Ula
Gast
|
| Ula Verfasst am: 11. Mai 2014 14:46 Titel: |
|
|
|
ALso bei der Lagrange Funktion steht da phi-punkt ², und wenn ich partielle Ableitung nach z mache, dann bleibt das da so stehen....[/latex] |
|
|
Ula
Gast
|
| Ula Verfasst am: 11. Mai 2014 15:18 Titel: |
|
|
Also dann müsste die Zwangskraft so berechnet werden:
Ist es so? |
|
|
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
| as_string Verfasst am: 11. Mai 2014 23:07 Titel: |
|
|
Ja, Du hast Recht... Ich hatte das Quadrat irgendwo verschluckt auf dem weg. Deine Winkelgeschwindigkeit ist mE richtig.
Bei der letzten würde ich das aber eher etwas einfacher rechnen: Du hast ja eine Kreisbewegung und die Winkelgeschwindigkeit schon ausgerechnet. Außerdem kennst Du den Radius dieser Kreisbahn:  . Du Weißt also, dass eine Komponente der Zwangskraft (in horizontaler Richtung) gerade die Zentripetalkraft sein muss, die die Masse auf der Kreisbahn hält, also 
Außerdem wirkt in vertikaler Richtung noch die Gewichtskraft, bzw. die Zwangskraft muss diese ja aufheben, indem sie eine vertikaler Komponente hat, die gleich groß aber nach oben gerichtet ist.
Mit Pythagoras sollte man diese beiden Komponenten ja zu einem Betrag zusammen bekommen können.
Du kannst zur Kontrolle dann mal schauen: Diese Zwangskraft muss ja auf jeden Fall senkrecht auf die Kegel-Innenfläche stehen. Der Winkel zu der Horizontalen von dieser Kraft sollte also gerade  entsprechen. Wenn alles richtig gerechnet ist, sollte also bei:
 gerade  raus kommen.
Gruß
Marco |
|
|
Ula
Gast
|
| Ula Verfasst am: 11. Mai 2014 23:41 Titel: |
|
|
Ok, das ist eigentlich alles nachvollziehbar.
Die Zwangskraft:
 } ) .
Jetzt noch die Aufgabe e).
WIe berechne ich die elementare Ableitung von
 ?
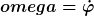DANKE!
Gruß,
Ula |
|
|
|
Registrieren
Login
FAQ
Suchen
