| Autor |
Nachricht |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 05. Jul 2017 18:29 Titel: Bewegungsgleichung lösen Silencium92 Verfasst am: 05. Jul 2017 18:29 Titel: Bewegungsgleichung lösen |
 |
|
Guten Tag,
gegeben sei der Hamiltonoperator eines "verschobenen" harmonischen Oszillator:

Ich soll die Bewegungsgleichungen aufstellen und diese lösen.
Die Bewegungsgleichung ist ja definiert als:
)
Ich habe noch keine Bewegungsglg. im Heisenbergbild gelöst und weiß um ehrlich zu sein, jetzt nicht genau was ich machen muss.
Soll ich in die Bewegungsgleichung (1) jeweils

einsetzen und lösen? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 05. Jul 2017 20:21 Titel: Re: Bewegungsgleichung lösen index_razor Verfasst am: 05. Jul 2017 20:21 Titel: Re: Bewegungsgleichung lösen |
 |
|
| Silencium92 hat Folgendes geschrieben: | Guten Tag,
gegeben sei der Hamiltonoperator eines "verschobenen" harmonischen Oszillator:

Ich soll die Bewegungsgleichungen aufstellen und diese lösen.
Die Bewegungsgleichung ist ja definiert als:
)
|
Wenn ich mich nicht täusche, hat der Kommutator das falsche Vorzeichen.
| Zitat: |
Ich habe noch keine Bewegungsglg. im Heisenbergbild gelöst und weiß um ehrlich zu sein, jetzt nicht genau was ich machen muss.
Soll ich in die Bewegungsgleichung (1) jeweils

einsetzen und lösen? |
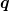 und und 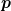 würden reichen. Wenn du die Zeitentwicklung für würden reichen. Wenn du die Zeitentwicklung für 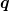 kennst, kennst du auch die für kennst, kennst du auch die für  . Aus demselben Grund macht es, denke ich, nicht viel Sinn, die Bewegungsgleichung für . Aus demselben Grund macht es, denke ich, nicht viel Sinn, die Bewegungsgleichung für 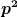 zu lösen. zu lösen. |
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 06. Jul 2017 15:59 Titel: Silencium92 Verfasst am: 06. Jul 2017 15:59 Titel: |
 |
|
Hallo razor,
danke für den Tipp und ja in "meiner" Heisenberggleichung fehlt ein minus.
a) Die Bewegungsgleichungen sollten wie folgt aussehen
 \quad \land \quad \frac{d}{dt}\hat{p}_H = \frac{1}{i\hbar}[\hat{p}_H,\hat{H}] \quad (2) )
, weil die Operatoren 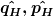 nicht explizit von der Zeit abhängen und somit die partielle Ableitung 0 ist. nicht explizit von der Zeit abhängen und somit die partielle Ableitung 0 ist.
b) Bewegungsgleichungen Lösen
zu (1) 
Im Text ist nicht genau angegeben, was f ist. Deshalb habe ich es einfach als Konstante angenommen.
zu (2) 
Ist das bis dahin alles korrekt?
Zuletzt bearbeitet von Silencium92 am 06. Jul 2017 18:13, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 06. Jul 2017 17:21 Titel: index_razor Verfasst am: 06. Jul 2017 17:21 Titel: |
 |
|
Nicht ganz. Auf der rechten Seite von (2) ist die Konstante f verlorengegangen. Ansonsten stimmt es mit meiner Rechnung überein.
Übrigens kannst du auch durch Vergleich mit den klassischen Hamiltonschen Gleichungen prüfen, ob das Ergebnis plausibel ist. |
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 06. Jul 2017 18:20 Titel: Silencium92 Verfasst am: 06. Jul 2017 18:20 Titel: |
 |
|
Habe es korrigiert.


Wow, ist das Zufall?
Zuletzt bearbeitet von Silencium92 am 06. Jul 2017 18:35, insgesamt einmal bearbeitet |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 06. Jul 2017 18:34 Titel: Silencium92 Verfasst am: 06. Jul 2017 18:34 Titel: |
 |
|
So jetzt muss ich die DGL (abgekürzte Schreibweise)
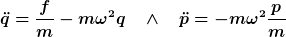
lösen.
Die DGL lassen sich dann relativ einfach lösen.
Jetzt kommt noch die letzte Teilaufgabe.
Geben Sie die Lösung in der Impulsdarstellung an.
Wie mache ich das? Im Schrödinger Bild, konnte man eine Fouriertrafo machen. Gibt es sowas auch im Heisenbergbild?
Zuletzt bearbeitet von Silencium92 am 06. Jul 2017 18:38, insgesamt 2-mal bearbeitet |
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 06. Jul 2017 18:36 Titel: Silencium92 Verfasst am: 06. Jul 2017 18:36 Titel: |
 |
|
Ahh, wenn das mein ehemaliger Dozent für Theoretische Mechanik gesehen hätte  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 06. Jul 2017 18:39 Titel: jh8979 Verfasst am: 06. Jul 2017 18:39 Titel: |
 |
|
| Silencium92 hat Folgendes geschrieben: |
Jetzt kommt noch die letzte Teilaufgabe.
Geben Sie die Lösung in der Impulsdarstellung an.
|
Versteh ich nicht. Kannst Du die ganze Aufgabe mal hier reinstellen? |
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 06. Jul 2017 19:03 Titel: Silencium92 Verfasst am: 06. Jul 2017 19:03 Titel: |
 |
|
Gegeben sei der Hamiltonoperator eines "verschobenen" harmonischen Oszillator:

a) Bestimmen Sie die Heisenbergschen Bewegungsgleichungen
b) Lösen Sie diese Gleichungen
c) Geben Sie die Lösung in der Impulsdarstellung an |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 06. Jul 2017 19:28 Titel: jh8979 Verfasst am: 06. Jul 2017 19:28 Titel: |
 |
|
| Silencium92 hat Folgendes geschrieben: | Gegeben sei der Hamiltonoperator eines "verschobenen" harmonischen Oszillator:

a) Bestimmen Sie die Heisenbergschen Bewegungsgleichungen
b) Lösen Sie diese Gleichungen
c) Geben Sie die Lösung in der Impulsdarstellung an |
Danke. Aber versteh ich immer noch nicht... trotz jahrelangem Physikstudium... 
Vllt will er einfach fass Du p durch p und q durch Ableitung nach p ersetzt... keine Ahnung was der Teil soll. |
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 06. Jul 2017 20:16 Titel: Silencium92 Verfasst am: 06. Jul 2017 20:16 Titel: |
 |
|
Gern geschehen.
Ich frage morgen mal nach. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 06. Jul 2017 21:40 Titel: index_razor Verfasst am: 06. Jul 2017 21:40 Titel: |
 |
|
Sehr offensichtlich finde ich die Fragestellung auch nicht. Es könnte aber folgendes gemeint sein.
Im Heisenbergbild hängen die (verallgemeinerten) Impulseigenzustände 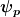 von der Zeit ab.*) Daraus folgt eine Bewegungsgleichung für die Funktion von der Zeit ab.*) Daraus folgt eine Bewegungsgleichung für die Funktion =\langle \psi_{p'}(0)|\psi_p(t)\rangle) . Die findest du, wenn du in die Eigenwertgleichung . Die findest du, wenn du in die Eigenwertgleichung
|\psi_p(t)\rangle =p|\psi_p(t)\rangle )
die Lösung aus der vorigen Aufgabe einsetzt. Zum Zeitpunkt  ist ist
= \langle \psi_{p'}(0)|\psi_p(0)\rangle=\delta(p'-p).)
Das ist die Anfangsbedingung. Ist das eine plausible Interpretation der Aufgabenstellung? Ich habe noch nicht ausprobiert, ob man da auf was lösbares kommt, also vielleicht solltest du wirklich vorher nochmal nachfragen, wenn du es nicht einfach so aus Spaß mal versuchen willst.
________
*) Das muß so sein, da die Eigenwerte 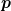 in in
|\psi_p\rangle = p|\psi_p\rangle.)
konstant sind. Würden sich die Eigenzustände nicht ändern, könnte man leicht einen Widerspruch zu den Heisenbergschen Bewegungsgleichungen ableiten. |
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 07. Jul 2017 15:59 Titel: Silencium92 Verfasst am: 07. Jul 2017 15:59 Titel: |
 |
|
Man soll die Operatoren, welche in den Lösungen der DGL
| Zitat: | 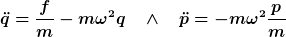 |
 &= A\cos(\sqrt{m}\omega t) + B\sin(\sqrt{m}\omega t) +\frac{f}{m^2 \omega^2} )
 &= C \cos(\omega t) + D \sin(\omega t))
auftauchen, in der Impulsdarstellung angeben.
Er hatte noch gesagt, dass in der Impulsdarstellung folgendes gilt:
> = i\hbar \frac{d}{dp}|\psi(p)> \quad \land \quad \hat{p}|\psi(p)> = p|\psi(p) )
In den obigen Lösungen der DGL tauchen die Operatoren aber nicht auf...
Versteht ihr, was er gemeint hat? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 07. Jul 2017 18:24 Titel: index_razor Verfasst am: 07. Jul 2017 18:24 Titel: |
 |
|
Was bedeuten denn die Konstanten A, B, C, D bei dir? Sind sie alle unabhängig?
Wie ist der Zusammenhang zwischen den Operatoren im Schrödinger- und Heisenbergbild zur Zeit t=0? |
|
 |
Heisenberg93
Anmeldungsdatum: 31.10.2015
Beiträge: 93
|
 Heisenberg93 Verfasst am: 07. Jul 2017 18:38 Titel: Heisenberg93 Verfasst am: 07. Jul 2017 18:38 Titel: |
 |
|
|
Die Aufgabe in ihrer jetzigen Form ergibt keinen Sinn |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 07. Jul 2017 19:09 Titel: index_razor Verfasst am: 07. Jul 2017 19:09 Titel: |
 |
|
|
Wie kommst du darauf? Ich denke sie ergibt schon Sinn. |
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 07. Jul 2017 20:06 Titel: Silencium92 Verfasst am: 07. Jul 2017 20:06 Titel: |
 |
|
Ich habe einfach die beiden DGL gelöst.
| Zitat: | | Wie ist der Zusammenhang zwischen den Operatoren im Schrödinger- und Heisenbergbild zur Zeit t=0? |
Hmm, in der Aufgabe sind nur folgende Angaben enthalten
| Zitat: |
Gegeben sei der Hamiltonoperator eines "verschobenen" harmonischen Oszillator: ...
a) Bestimmen Sie die Heisenbergschen Bewegungsgleichungen
b) Lösen Sie diese Gleichungen
c) Geben Sie die Lösung in der Impulsdarstellung an
|
Es gibt keine Informationen über mögliche Randbedingungen. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 07. Jul 2017 22:27 Titel: index_razor Verfasst am: 07. Jul 2017 22:27 Titel: |
 |
|
| Silencium92 hat Folgendes geschrieben: | Ich habe einfach die beiden DGL gelöst.
|
Es gibt einen Zusammenhang zwischen p und q, den du nicht berücksichtigt hast.

| Zitat: |
| Zitat: | | Wie ist der Zusammenhang zwischen den Operatoren im Schrödinger- und Heisenbergbild zur Zeit t=0? |
Hmm, in der Aufgabe sind nur folgende Angaben enthalten
|
Verwende doch einfach die Definition des Heisenbergbildes.

Was ist 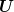 ? Das ist Grundwissen. Das wird nicht in jeder Aufgabe wiederholt. ? Das ist Grundwissen. Das wird nicht in jeder Aufgabe wiederholt.
| Zitat: |
Es gibt keine Informationen über mögliche Randbedingungen. |
Doch, die gibt es. Sie folgt m.E. aus der Definition des Heisenbergbildes. |
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 07. Jul 2017 23:11 Titel: Silencium92 Verfasst am: 07. Jul 2017 23:11 Titel: |
 |
|
| Zitat: | Es gibt einen Zusammenhang zwischen p und q, den du nicht berücksichtigt hast.

|
Ich habe diesen Zusammenhang benutzt, um aus den beiden gekoppelten DGL erster Ordnung
| Zitat: | 

|
zwei ungekoppelte DGL zweiter Ordnung zu erhalten
| Zitat: |
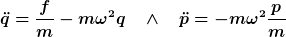
|
.
Dessen Lösungen ich hingeschrieben hatte. Ich mache wahrscheinlich irgendwo einen Denkfehler oder verstehe deinen Hinweis nicht.
| Zitat: | Was ist 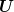 |
Das ist der Zeitpropagator (auch Zeitentwicklungsoperator genannt).
Gruß
Alex |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Jul 2017 09:10 Titel: index_razor Verfasst am: 08. Jul 2017 09:10 Titel: |
 |
|
Zunächst hätte mir wahrscheinlich früher auffallen sollen, daß deine Bewegungsgleichung für q einen Fehler enthält. Rechne noch mal nach. Es müßte

rauskommen. Damit mußt du deine Lösung korrigieren.
So, nun müssen wir allerdings diese Gleichung gar nicht nach Schema F für gewöhnliche inhomogene DGL mit konstanten Koeffizienten lösen. Denn wir haben schon die Lösung für p
 + D\sin(\omega t))
und wir wissen, daß

d.h. da steht unsere Lösung für q. Wir müssen nur noch einsetzen. Wie lautet das Ergebnis?
Ich muß noch auf einen logischen Fehler eingehen, den du hier begehst. Unser Problem besteht ja darin die allgemeine Lösung für die gekoppelten Bewegungsgleichungen

und

zu finden. Wir haben nun durch nochmaliges Ableiten die Gleichungen entkoppelt. Diese entkoppelten Gleichungen lassen sich einfacher lösen, sie sind aber redundant. Nicht jede allgemeine Lösung der beiden entkoppelten Gleichungen führt automatisch auf eine Lösung des ursprünglichen gekoppelten Systems.*) Das müssen wir durch Einsetzen der Lösung nochmal prüfen.
| Silencium92 hat Folgendes geschrieben: |
| Zitat: | Was ist 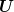 |
Das ist der Zeitpropagator (auch Zeitentwicklungsoperator genannt).
|
Wie lautet er denn explizit für die Transformation vom Schrödingerbild ins Heisenbergbild? Welche Form hat er bei t=0?
______________
*) Ähnliche Sorgfalt mußt du z.B. bei der Ableitung der Wellengleichung aus den Maxwellgleichungen aufwenden. Man bildet nochmal die Rotation und erhält zwei unabhängige Gleichungen für E und B. Dann muß man die Lösungen dieser beiden Wellengleichungen aber nochmal in die Maxwellgleichungen ensetzen und bekommt die Bedingung, daß E orthogonal zu B stehen muß. Andere Winkel sind von den Maxwellgleichungen verboten, und deshalb unphysikalisch, aber von den entkoppelten Gleichungen nicht ausgeschlossen. |
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 08. Jul 2017 10:30 Titel: Silencium92 Verfasst am: 08. Jul 2017 10:30 Titel: |
 |
|
- C\sin(\omega t)) \quad \Rightarrow \quad q = -\frac{ (D\cos(\omega t)- C\sin(\omega t))}{m\omega} +\frac{f}{m\omega^2})
Komisch, wenn ich die Ableitung bilde, erhalte ich folgendes:

| Zitat: | | Diese entkoppelten Gleichungen lassen sich einfacher lösen, sie sind aber redundant. |
Hier liegt also ein solcher Fall vor (falls ich mich nicht verrechnet habe). Wie komme ich den jetzt an eine "richtige" Lsg. ?
 = e^{-\frac{i}{\hbar}\hat{H}(t-t_0)}= e^{-\frac{i}{\hbar}\hat{H}t} )
| Zitat: | | Wie lautet er denn explizit für die Transformation vom Schrödingerbild ins Heisenbergbild? |
 \hat{F}_S \hat{U}(t,t_0) \quad \quad |\psi_H> = {U}^\dagger(t,t_0) |\psi(t)_S>)
Wobei ) der adjungierte Operator ist. der adjungierte Operator ist. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Jul 2017 11:15 Titel: index_razor Verfasst am: 08. Jul 2017 11:15 Titel: |
 |
|
| Silencium92 hat Folgendes geschrieben: | - C\sin(\omega t)) \quad \Rightarrow \quad q = -\frac{ (D\cos(\omega t)- C\sin(\omega t))}{m\omega} +\frac{f}{m\omega^2})
|
Das sieht richtig aus.
| Zitat: |
Komisch, wenn ich die Ableitung bilde, erhalte ich folgendes:

|
Nein, das stimmt nicht.
| Zitat: |
| Zitat: | | Diese entkoppelten Gleichungen lassen sich einfacher lösen, sie sind aber redundant. |
Hier liegt also ein solcher Fall vor (falls ich mich nicht verrechnet habe). Wie komme ich den jetzt an eine "richtige" Lsg. ?
|
Du hast die Lösung doch gerade, meiner Beschreibung folgend, selbst hingeschrieben. Es kommt mir so vor, als wäre dir gar nicht klar, was du da eigentlich rechnest.
Jetzt müssen wir uns eigentlich nur noch um die Anfangsbedingungen kümmern...
| Zitat: |
 = e^{-\frac{i}{\hbar}\hat{H}(t-t_0)}= e^{-\frac{i}{\hbar}\hat{H}t} )
|
Ich frage danach, wegen deiner Bemerkung über die fehlenden Anfangsbedingungen. Die entscheidende Frage hast du nun wieder nicht beantwortet: Wie sieht die Transformation bei t=0 aus? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Jul 2017 21:50 Titel: index_razor Verfasst am: 08. Jul 2017 21:50 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
| Zitat: |
Komisch, wenn ich die Ableitung bilde, erhalte ich folgendes:

|
Nein, das stimmt nicht.
|
Der Fehler ist wahrscheinlich, daß du beim Ableiten irgendwann die Konstanten C und D vor den Winkelfunktionen vertauscht hast.
Hier vielleicht zur Motivation und damit du weißt, in welche Richtung du ungefähr zielen mußt, meine Lösung zum Vergleich (Fehler natürlich nicht ausgeschlossen)
=\sin(\omega t)\frac{p}{m\omega} - \cos(\omega t)\left(\frac{f}{m\omega^2} - i \frac{\partial}{\partial p}\right) + \frac{f}{m\omega^2}
<br />
)
=\cos(\omega t)p + \sin(\omega t)\left(\frac{f}{\omega}-i m\omega\frac{\partial}{\partial p}\right)
<br />
) |
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 11. Jul 2017 09:23 Titel: Silencium92 Verfasst am: 11. Jul 2017 09:23 Titel: |
 |
|
- C\sin(\omega t))}{m\omega} +\frac{f}{m\omega^2})
Hieraus folgt:
 - \omega C \cos(\omega t)}{m \omega}= \frac{C\cos(\omega t)+D\sin(\omega t)}{m}=\frac{p}{m})
Damit ich habe jetzt beide Lsg. gefunden.
Zur Randbedingung:
Die Transformation für t=0 sieht so aus.
>) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 11. Jul 2017 09:53 Titel: index_razor Verfasst am: 11. Jul 2017 09:53 Titel: |
 |
|
| Silencium92 hat Folgendes geschrieben: |
Zur Randbedingung:
Die Transformation für t=0 sieht so aus.
>) |
Ja, die Zustände interessieren uns allerdings gerade weniger als die Transformationen der Operatoren
 = U(t)^\dagger q_S U(t))
also für t=0
 = q_S)
usw. Wie lauten nun die beiden Schrödinger-Operatoren für Ort und Impuls in der Impulsdarstellung? Ist dir klar, wie du jetzt weiter machen mußt? |
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 11. Jul 2017 10:25 Titel: Silencium92 Verfasst am: 11. Jul 2017 10:25 Titel: |
 |
|
Ich bin mir nicht sicher 
Also die beiden Lsg. für die Operatoren im Heisenbergbild lauten:
 = -\frac{ (D\cos(\omega t)- C\sin(\omega t))}{m\omega} +\frac{f}{m\omega^2})
=C\cos(\omega t) + D\sin(\omega t))
| Zitat: | | Wie lauten nun die beiden Schrödinger-Operatoren für Ort und Impuls in der Impulsdarstellung? |
> = i\hbar \frac{d}{dp}|\psi(p)> \quad \land \quad \hat{p}|\psi(p)> = p|\psi(p) )
Jetzt weiß ich, dass
| Zitat: |
also für t=0
 = q_S) |
Also kann ich die Konstanten wie folgt bestimmen:
 = - \frac{D}{m \omega} + \frac{f}{m\omega^2} = q_s=i\hbar \frac{d}{dp} \quad \Rightarrow \quad -\frac{D}{m\omega}=i\hbar \frac{d}{dp} - \frac{f}{m\omega^2})

 = C = p_s = p )
Ist das so korrekt? |
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 11. Jul 2017 16:07 Titel: Silencium92 Verfasst am: 11. Jul 2017 16:07 Titel: |
 |
|
Ich kam heute morgens nicht mehr dazu, die Gleichungen in der Impulsdarstellung hinzuschreiben.
Aus
 = -\frac{ (D\cos(\omega t)- C\sin(\omega t))}{m\omega} +\frac{f}{m\omega^2})
=C\cos(\omega t) + D\sin(\omega t))
wird dann
 = -\frac{ (\frac{f}{m} - i\hbar m\omega \frac{d}{dp})\cos(\omega t)- p\sin(\omega t))}{m\omega} +\frac{f}{m\omega^2})
=p\cos(\omega t) + (\frac{f}{m} - i\hbar m\omega \frac{d}{dp})\sin(\omega t))
Diese Lösung stimmt aber nicht mit deiner über ein
| Zitat: | =\sin(\omega t)\frac{p}{m\omega} - \cos(\omega t)\left(\frac{f}{m\omega^2} - i \frac{\partial}{\partial p}\right) + \frac{f}{m\omega^2}
<br />
)
=\cos(\omega t)p + \sin(\omega t)\left(\frac{f}{\omega}-i m\omega\frac{\partial}{\partial p}\right)
<br />
) |
Kann es sein, dass du bei D das h quer vergessen hast oder habe ich einen Fehler gemacht? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 11. Jul 2017 17:34 Titel: index_razor Verfasst am: 11. Jul 2017 17:34 Titel: |
 |
|
| Silencium92 hat Folgendes geschrieben: |
Kann es sein, dass du bei D das h quer vergessen hast oder habe ich einen Fehler gemacht? |
Naja, vergessen nicht gerade. Damit man solche Konstanten nicht durch die ganze Rechnung schleifen muß, ist es üblich in Einheiten mit 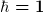 zu rechnen. zu rechnen.
| Zitat: |
 = -\frac{ (\frac{f}{m} - i\hbar m\omega \frac{d}{dp})\cos(\omega t)- p\sin(\omega t))}{m\omega} +\frac{f}{m\omega^2})
=p\cos(\omega t) + (\frac{f}{m} - i\hbar m\omega \frac{d}{dp})\sin(\omega t))
|
In ) vor dem Sinus und in vor dem Sinus und in ) vor dem Kosinus ist der Term vor dem Kosinus ist der Term  falsch. Da hast du dich aber offenbar nur vertippt. Sonst scheint alles zu stimmen. falsch. Da hast du dich aber offenbar nur vertippt. Sonst scheint alles zu stimmen. |
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 11. Jul 2017 20:30 Titel: Silencium92 Verfasst am: 11. Jul 2017 20:30 Titel: |
 |
|
Ich sehe gerade nicht warum der f/m-Term falsch ist. D ist doch wie folgt definiert:

Und das habe ich jeweils in die Lsg. eingesetzt. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 11. Jul 2017 20:44 Titel: index_razor Verfasst am: 11. Jul 2017 20:44 Titel: |
 |
|
Weiter oben hattest du noch geschrieben:
| Silencium92 hat Folgendes geschrieben: |

|
Eine Zeile später stimmt's nicht mehr. Du hast falsch gekürzt. f/m kann übrigens schon deshalb nicht stimmen, weil f eine Kraft ist und Kraft pro Masse eine Beschleunigung ergibt, aber keinen Impuls. |
|
 |
Silencium92
Anmeldungsdatum: 24.01.2017
Beiträge: 59
|
 Silencium92 Verfasst am: 12. Jul 2017 13:14 Titel: Silencium92 Verfasst am: 12. Jul 2017 13:14 Titel: |
 |
|
Oh man, wieder ein unnötiger Rechenfehler meinerseits...
Nichts desto trotz, vielen Dank für deine Hilfe und Geduld. |
|
 |
|

















