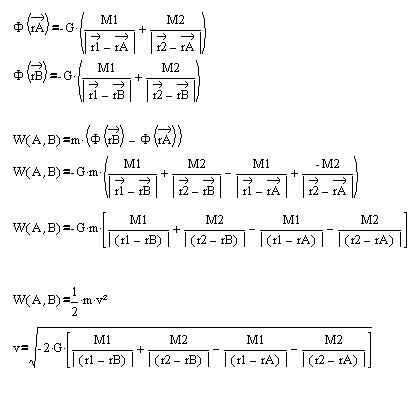| Autor |
Nachricht |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 17. Okt 2004 10:13 Titel: Potential bei mehreren Gravitationszentren para Verfasst am: 17. Okt 2004 10:13 Titel: Potential bei mehreren Gravitationszentren |
 |
|
Hallo,
normalerweise betrachtet man Arbeit eines Körpers im Gravitationsfeld ja im Bezug auf ein Gravitationszentrum, womit für die Änderung der kinetischen Energie gilt: ΔE=f(Δr).
Jetzt habe ich aber statt einem Gravitationszentrum aber noch ein zweites. Wie kann ich dann die Arbeit errechnen, wenn ich den Körper vom Punkt A zum Punkt B (beide außerhalb der Gravitationszentren) bewege (bzw. er sich selbst bewegt)?
Para.
_________________
Formeln mit LaTeX
Zuletzt bearbeitet von para am 14. Mai 2006 13:52, insgesamt einmal bearbeitet |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 17. Okt 2004 11:33 Titel: Nikolas Verfasst am: 17. Okt 2004 11:33 Titel: |
 |
|
Mal eine Idee (weiss aber nicht, ob's wirklich simmt):
Wende das Prinzip der ungestörten Superposition an. Also ein Zentrum abschalten, Energier ausrechnen, anderes Zentrum ausschalten, diese Enerdie berechnen und dann diese Energien addieren. (?)
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
dachdecker2
Administrator

Anmeldungsdatum: 15.06.2004
Beiträge: 1174
Wohnort: Zeppelinheim / Hessen
|
 dachdecker2 Verfasst am: 17. Okt 2004 15:09 Titel: dachdecker2 Verfasst am: 17. Okt 2004 15:09 Titel: |
 |
|
Die Arbeit im Gravitationsfeld ist doch genau so groß, wie der Unterschied der Bahnenergien, die jewwils zu den Zuständen vorher und nachher gehören, oder?
Jetzt würde ich mal behaupten wollen, das man beim eingeschränkten 3-Körperproblem nur Bahnenergien für sehr kleine Bahnen um einen der beiden Zentralkörper und Bahnenergien für sehr große Bahnen um beide Zentralkörper annehernd angeben kann. Bahnen, die an in geringer Entfernung zu beiden Zentralkörpern vorbeiführen, ändert sich der Bahnstaus bestimmt unentwegt. Außerdem gibt es in diesem Bereich keine stabilen Bahnen.
Du wirst vielleicht unter Umständen die Gravitationsarbeit angeben können, aber viel bringen wird die Zahl sicherlich nicht...
_________________
Gruß, dachdecker2
http://rettedeinefreiheit.de |
|
 |
Meromorpher

Anmeldungsdatum: 09.03.2004
Beiträge: 388
|
 Meromorpher Verfasst am: 17. Okt 2004 15:24 Titel: Meromorpher Verfasst am: 17. Okt 2004 15:24 Titel: |
 |
|
@toxman:
da muss man aber vorsichtig sein, die vorzeichen genau zu betrachten.
exakter ist es das feld, nicht das potential, mit linearer superposition (addieren) zu berechnen, und dann einfach über den weg integrieren.
@dachdecker: so wie ich das verstehe kennt er die bahn schon und will nur die energie berechnen..
|
|
 |
dachdecker2
Administrator

Anmeldungsdatum: 15.06.2004
Beiträge: 1174
Wohnort: Zeppelinheim / Hessen
|
 dachdecker2 Verfasst am: 17. Okt 2004 15:25 Titel: dachdecker2 Verfasst am: 17. Okt 2004 15:25 Titel: |
 |
|
Ich habe es mir nicht von nahem angeschaut, aber kann man sich sicher sein, das der Weg egal ist?
_________________
Gruß, dachdecker2
http://rettedeinefreiheit.de |
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 17. Okt 2004 15:37 Titel: para Verfasst am: 17. Okt 2004 15:37 Titel: |
 |
|
Mein Problem ist etwa der Natur, dass eine Probemasse (sehr klein) von zwei Gravitationszentren angezogen wird. Die Probemasse bewegt sich auf einer festen Bahn (wird also geführt), von Punkt A nach B. Dabei passiert diese eins der Gravi-Zentren, entfernt sich jedoch auch wieder von diesem. Letztendlich ist die Probemasse also im Punkt B angelangt. Jetzt interessiert mich die Geschwindigkeit, die dir Probemasse im Punkt B erreicht hat.
Natürlich könnte ich jeweils die Kräfte in Richtung der Gravi-Zentren vektoriell addieren, die Komponente in Bewegunsrichtung ermitteln, und dann über den Weg integrieren, aber wenn man einfache Ausdrücke für die potentielle Energie am Punkt A und dem Punkt B machen könnte, könnte ich mir das sparen - und: Die Faulheit ist der Menschheit größter Antrieb *g*
_________________
Formeln mit LaTeX |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 17. Okt 2004 17:02 Titel: Nikolas Verfasst am: 17. Okt 2004 17:02 Titel: |
 |
|
Studierst du, oder wo bekommst du solche Aufgaben gestellt? Das hört sich ja richtig interessant an. 
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
albega

Anmeldungsdatum: 08.03.2004
Beiträge: 11
|
 albega Verfasst am: 17. Okt 2004 18:57 Titel: albega Verfasst am: 17. Okt 2004 18:57 Titel: |
 |
|
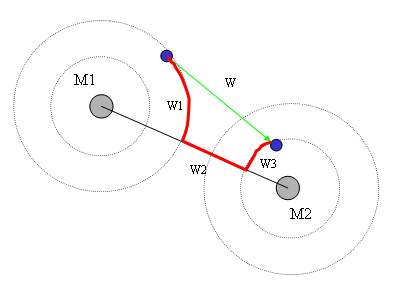
Vielleicht könnte man das Problem vereinfachen, wenn man den Weg ersetzt, wie in der
angehängten Skizze. Die Arbeit W1 hängt nur von der Kraft in Richtung M2 ab, da sich der
Körper auf einer Äquipotentialebene von M1 bewegt. Analoges gilt für W3. Und W2 dürfte relativ
einfach zu berechnen sein, da sich der Körper hier auf der direkten Verbindungslinie der
beiden Massezentren bewegt.
MfG
Albega
| Beschreibung: |
|
| Dateigröße: |
12.1 KB |
| Angeschaut: |
8242 mal |
|
|
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 17. Okt 2004 19:48 Titel: para Verfasst am: 17. Okt 2004 19:48 Titel: |
 |
|
In der Skizze sind beide Zentren von einem homogenen Feld umgeben - ist es nicht aber so, dass sich die Felder überlagern?
Naja, ich glaube ich werd' erstmal fleißig integrieren und dann schauen, ob ein einfacherer Lösungsweg zum gleichen Ergebnis führt.
_________________
Formeln mit LaTeX |
|
 |
Nikolas
Ehrenmitglied

Anmeldungsdatum: 14.03.2004
Beiträge: 1873
Wohnort: Freiburg im Brsg.
|
 Nikolas Verfasst am: 17. Okt 2004 20:12 Titel: Nikolas Verfasst am: 17. Okt 2004 20:12 Titel: |
 |
|
Die beiden Felder überlagern sich natürlich, aber der Trick von Albega war einfach, das es sich auf bis auf den Strich in der Mitte immer auf ein Aquipotentialfläche eines Zentrums bewegt hat und es somit ausgeschaltet hat.
_________________
Nikolas, the mod formerly known as Toxman.
Erwarte das Beste und sei auf das Schlimmste vorbereitet. |
|
 |
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
 Bruce Verfasst am: 18. Okt 2004 09:24 Titel: Bruce Verfasst am: 18. Okt 2004 09:24 Titel: |
 |
|
Das -1/r^2 Kraftgesetz des Garavitationsfeldes gehört zu einem konservativen
Kraftfeld, d.h. die wirkende Kraft in einem Punkt des Kraftfeldes kann aus
einer skalaren Potentialfunktion durch Gradientenbildung berechnet werden.
Die besondere Eigenschaft eines konservativen Kraftfeldes liegt darin, daß
die Arbeit W(A,B), die aufgebracht werden muß, um einen Probekörper im
Kraftfeld vom Punkt A zum Punkt B zu bewegen, unabhängig vom durchlaufenen
Weg von A nach B ist. Mathematisch wird dies dadurch ausgedrückt, daß

für das Wegintegral der Kraft entlang einer beliebigen geschlossenen Kurve C gilt.
Für das konkrete Problem von Para ist dieses Potential durch
\;=\;-Gm\, \left(\frac{M_1}{|\vec{r_1}-\vec{r}|}\,+\,\frac{M_2}{|\vec{r_2}-\vec{r}|} \right))
gegeben. Die Vektoren r1 und r2 sind die Ortsvektoren der Gravitationszentren.
Für die Arbeit W(A,B), die für die Verschiebung des Probekörpers vom Punkt rA
zum Punkt rB aufgewandt werden muß, gilt:
\;=\;\Phi(\vec{r}_B)-\Phi(\vec{r}_A).)
Gruß von Bruce
|
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 18. Okt 2004 15:45 Titel: para Verfasst am: 18. Okt 2004 15:45 Titel: |
 |
|
Was Vektorrechnung anbelangt bin ich noch nicht so weit - ich denke ich verstehe aber den Kern. Aber wofür steht das r, wenn r1 und r2 bereits die "Abstände" zu den Gravi-Zentren kennzeichnen?
Wäre es evt. auch ein Ansatz, den Schwerpunkt beider Zentren zu bilden, so dass man sich die Gesamtmasse in diesem Punkt konzentriert denkt? Dann müsste man die pot. Energie nur noch im Bezug auf ein Zentrum bestimmen und könnte die Differenz ebenfalls leicht bilden.
_________________
Formeln mit LaTeX |
|
 |
albega

Anmeldungsdatum: 08.03.2004
Beiträge: 11
|
|
 |
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
 Bruce Verfasst am: 18. Okt 2004 19:53 Titel: Bruce Verfasst am: 18. Okt 2004 19:53 Titel: |
 |
|
@para
Vergiß die Idee mit dem Schwerpunkt, das funktioniert nur im Fall einer
radialsymmetrischen Massenverteilung!
Die Vektoren r, r1 und r2 beziehen sich auf den Ursprung eines beliebig
vorgegebenen kartesischen Koordinatensystems. r ist der Ortsvektor
eines beliebigen Punktes und r1, r2 sind die Ortsvektoren der Massenzentren
M1 und M2.
Gruß von Bruce
|
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 18. Okt 2004 20:57 Titel: para Verfasst am: 18. Okt 2004 20:57 Titel: |
 |
|
| Bruce hat Folgendes geschrieben: | | Vergiß die Idee mit dem Schwerpunkt, das funktioniert nur im Fall einer radialsymmetrischen Massenverteilung! |
Ok ... dann mach ich mal mit den Vektoren los.
_________________
Formeln mit LaTeX |
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 23. Okt 2004 19:52 Titel: para Verfasst am: 23. Okt 2004 19:52 Titel: |
 |
|
| Bruce hat Folgendes geschrieben: |
Für das konkrete Problem von Paranoia ist dieses Potential durch
\;=\;-Gm\,\left(\frac{M_1}{|\vec{r_1}-\vec{r}|}\,+\,\frac{M_2}{|\vec{r_2}-\vec{r}|}\right))
gegeben. Die Vektoren r1 und r2 sind die Ortsvektoren der Gravitationszentren.
Für die Arbeit W(A,B), die für die Verschiebung des Probekörpers vom Punkt rA
zum Punkt rB aufgewandt werden muß, gilt:
\;=\;\Phi(\vec{r}_B)-\Phi(\vec{r}_A).) |
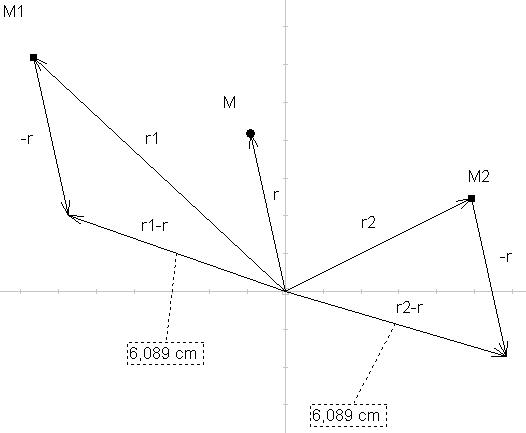
Ich hab' mir das mal angeschaut. Dabei hat sich allerding s bei mir eine Frage ergeben.
Angenommen M1 und M2 sind gleich groß, dann heben sich die Gravitationskräfte zwischen diesen Massen genau auf, wenn sich der Probekörper exakt in der Mitte der beiden befindet. Müsste dann aber nicht auch das Potential gleich null sein? Wenn man das mit dieser Formel berechnet, gibt es keine Möglichkeit (außer wenn M1 und M2 zusammenfallen), auf dieses Ergebnis zu kommen. Oder sind meine Anschauungen zum Potential falsch?
| Beschreibung: |
M1, M2 ... Massen der Gravi-Zentren
M ... Probemasse, die bewegt werden soll
Vektoren nach Bruce, Koordinatensystem ist eingezeichnet. |
|
| Dateigröße: |
21.19 KB |
| Angeschaut: |
7345 mal |
|
_________________
Formeln mit LaTeX
Zuletzt bearbeitet von para am 14. Mai 2006 13:49, insgesamt einmal bearbeitet |
|
 |
dachdecker2
Administrator

Anmeldungsdatum: 15.06.2004
Beiträge: 1174
Wohnort: Zeppelinheim / Hessen
|
 dachdecker2 Verfasst am: 24. Okt 2004 09:16 Titel: dachdecker2 Verfasst am: 24. Okt 2004 09:16 Titel: |
 |
|
Definitionsgemäß ist das Potential im unendlichen null. Das bedeutet, dass das System keine (negative) otentielle Energie hat, wenn es ungebunden (also frei) ist. Da der Punkt zwischen den Massen aber im Gravitationstopf liegt, ordnet man im eine negative potentielle Energie zu.
Die Potentielle Energie alleine reicht aber nicht um den Zusatand der Probemasse zu beschreiben, da diese im Normalfall auch kinetische Energie beinhaltet. Potentielle und kinetische Energie werden kontinuierlich inenander Umgewandelt - Deswegen kann man vielleicht die Gesamtenergie (kinetiasche + potentielle) angeben. Ich würde aber meinen, das selbst das in einem 3-Körpersystem (oder einem höheren) nicht ausreicht, da die energie auch zwischen den Massen ausgetauscht wird... (Die Beschleunigen sich ja gegenseitig)
_________________
Gruß, dachdecker2
http://rettedeinefreiheit.de |
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 24. Okt 2004 11:41 Titel: para Verfasst am: 24. Okt 2004 11:41 Titel: |
 |
|
| dachdecker2 hat Folgendes geschrieben: | | Ich würde aber meinen, das selbst das in einem 3-Körpersystem (oder einem höheren) nicht ausreicht, da die energie auch zwischen den Massen ausgetauscht wird... (Die Beschleunigen sich ja gegenseitig) |
Vereinfachung: m<<M1, m<<M2, M1 und M2 verändern ihre Position nicht.
Um noch einmal auf meine Aufgabenstellung hinzuweisen: Ein Körper wird (wie auch immer) auf den Punkt A gesetzt (kinetische Energie=0) und bewegt sich dann auf einer definierten Bahn zum Punkt B ... jetzt ist die Frage, welche kinetische Energie er dort hat (was ja der Differenz der pot. Energien von A und B entsprechen dürfte).
_________________
Formeln mit LaTeX |
|
 |
dachdecker2
Administrator

Anmeldungsdatum: 15.06.2004
Beiträge: 1174
Wohnort: Zeppelinheim / Hessen
|
 dachdecker2 Verfasst am: 24. Okt 2004 12:00 Titel: dachdecker2 Verfasst am: 24. Okt 2004 12:00 Titel: |
 |
|
Wenn das so ist, dann hängt die kinetische Energie nachher davon ab, wie der körper beschleunigt wird. Da er sich ja auf einer Geraden bewegt, muss es eine Kraft geben, die ihn dort hält (sehe ich das richtig?). Dann kommt es noch auf die Masse der festgepinnten Massen an - es könnte ja sein (wie aus dem Bild ersichtlich) das der körper sich nicht in die "richtige" Richtung bewegen würde, weil der nähere Stern eine größere Kraft ausübt...
Kann Paranoia vielleicht eine detailierte Skizze zu seiner Frage machen, damit wir hier nicht so "ins Blaue" hineindiskutieren müssen?
Wäre es nicht am einfachsten, schnell ne Simulation zu programmieren? Vielleicht fällt einem dann auch ein, was mit den Beschleunigungsanteilen wird, die nicht in Richtung der Festgelegten Bahn zeigen... Hier gibts lauter offene Fragen bezüglich der gegebenen Bedingungen.
In 14 Tagen hab ich vielleicht ein bisschen Zeit zum proggen, da läge es nahe, dass ich mir die Sache mit den Lagrange-Punkten auch gleich mal anschaue  . .
Ich lass das Prob mal im Hinterkopf und poste dann hier ne Gleichung, wenn mir eine einfällt...
_________________
Gruß, dachdecker2
http://rettedeinefreiheit.de |
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
 para Verfasst am: 24. Okt 2004 13:40 Titel: para Verfasst am: 24. Okt 2004 13:40 Titel: |
 |
|
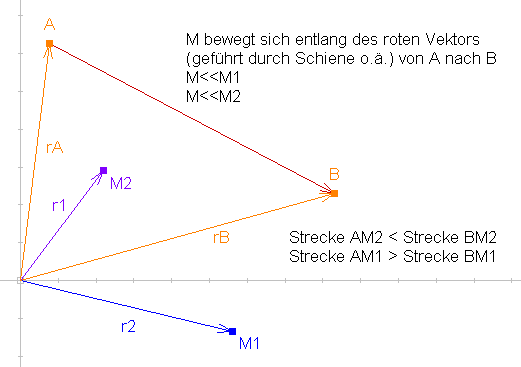
Eine Simulation würde ich nur ungern durchführen ... mathematisch korrekt wäre schöner, zumal ja nur der Endzustand interessiert.
Ich habe den Sachverhalt mal skizziert, ich hoffe dass es jetzt klar ist wie ich das meine ...
P.S: Wie der Körper auf seiner Bahn gehalten wird, ist erstmal zweitrangig ...
| Beschreibung: |
|
| Dateigröße: |
5.66 KB |
| Angeschaut: |
7322 mal |
|
_________________
Formeln mit LaTeX |
|
 |
dachdecker2
Administrator

Anmeldungsdatum: 15.06.2004
Beiträge: 1174
Wohnort: Zeppelinheim / Hessen
|
 dachdecker2 Verfasst am: 24. Okt 2004 14:48 Titel: dachdecker2 Verfasst am: 24. Okt 2004 14:48 Titel: |
 |
|
Ich denke, dass man damit schon was anfangen kann... Ich werd mir mal was einfallen lassen.
Könntest du mal noch schreiben, wo das vorkommt? Interessant sind auch die Zwangsbedingungen neben der Bewegungsbahn (also auch die unbewegten Massen). Würdest du die näherungsweise Lösung (Simulation) dann akzeptieren, wenn die symbolische Lösung nicht möglich wäre?
_________________
Gruß, dachdecker2
http://rettedeinefreiheit.de |
|
 |
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
 Bruce Verfasst am: 24. Okt 2004 22:01 Titel: Bruce Verfasst am: 24. Okt 2004 22:01 Titel: |
 |
|
@para
Deine Skizzen sehen vernünftig aus. Poste mal eine Rechnung, dann
kann ich dir sagen ob dein Ergebnis stimmt oder nicht.
@Dachdecker
Bevor Du anfängst zu rechnen, halte bitte noch mal inne und komme zur
Ruhe! Ich glaube Du denkst bei paras Problem zu kompliziert.
Er hat kein Dreikörperproblem!
Der Weg von A nach B spielt keine Rolle für die Änderung der
potentiellen Energie und deswegen kann die Änderung der
kinetischen Energie im Prinzip sehr einfach berechnet werden.
Wenn ich ihn richtig verstanden habe, dann sucht er ja nicht
den Geschwindigkeitsvektor im Endpunkt B sondern höchstens
den Betrag der Geschwindigkeit.
Gruß von Bruce.
|
|
 |
para
Moderator

Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
|
 |
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
 Bruce Verfasst am: 25. Okt 2004 21:11 Titel: Bruce Verfasst am: 25. Okt 2004 21:11 Titel: |
 |
|
@para
Dein Ergebnis sieht im wesentlichen richtig aus. Ein Schönheitsfehler
liegt darin, daß Du noch nicht weißt, welches Vorzeichen der Ausdruck
unter dem Wurzelzeichen hat. Deswegen schreibt man da besser
Betragsstriche und berücksichtigt dann das korrekte Vorzeichen
in der Änderung der kinetischen Energie. Die kann zu oder abnehmen.
Gruß von Bruce
|
|
 |
maxdull
Anmeldungsdatum: 26.10.2004
Beiträge: 26
|
 maxdull Verfasst am: 26. Okt 2004 04:35 Titel: maxdull Verfasst am: 26. Okt 2004 04:35 Titel: |
 |
|
Das mit dem Vorzeichen in der Wurzel stimmt nicht: Wird dieses negativ, so ist der Betrag der Geschwindigkeit imaginär. Dies bedeutet, dass der Körper nicht an diesen Punkt gelangen kann wenn seine kinetische Energie am Startpunkt Null ist wie in dieser Rechnung. Ist sie ungleich Null, so tritt sie als weiterer positiver Summand in der Wurzel auf.
Ferner: Es ist korrekt, dass sich die Kräfte in der Mitte zwischen zwei gleichen Massen aufheben, auch wenn das Potential nicht Null ist: In einem Vergleich mit Hügellandschaft entspricht dem Wert des Potentials die Höhe über Meer am entsprechenden Ort und die Geländeneigung entspricht der Kraft.
Gruss
|
|
 |
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
 Bruce Verfasst am: 26. Okt 2004 10:57 Titel: Bruce Verfasst am: 26. Okt 2004 10:57 Titel: |
 |
|
@maxdull
Das mit dem Vorzeichen meinst Du nicht ernst, oder?
Wenn die Änderung der kinetischen Energie negativ ist, dann hat
sich der Betrag der Geschwindigkeit verkleinert.
Es wurde nicht vorausgesetzt, daß die Masse ohne äußere
Kräfte von A nach B kommt. Es soll lediglich die Änderung
der potentiellen Energie berechnet werden und diese Änderung
ist wegunabhängig. Die einzigen Randbedingungen sind der
Anfangspunkt und der Endpunkt.
Gruß von Bruce.
@edit
Jetzt fällt mir auf, daß maxdull in einem Punkt recht hat. Die
Formel von para ist so nicht korrekt. Die Wurzel zu ziehen
ist riskant. Eigentlich gilt:
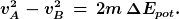
Deswegen muß man aufpassen.
Aber das gilt nur dann, wenn keine äußeren Kräfte wirken, d.h. wenn die
Bewegung der Masse m allein durch das Gravitationsfeld von mA und mB
beeinflußt wird. Sollte dann die Änderung der potentiellen Energie ein
anderes Vorzeichen habe als die Differenz der Geschwindigkeitsquadrate,
dann kann die Masse m im Punkt B nicht die Geschwindigkeit vB haben.
|
|
 |
maxdull
Anmeldungsdatum: 26.10.2004
Beiträge: 26
|
 maxdull Verfasst am: 27. Okt 2004 01:33 Titel: maxdull Verfasst am: 27. Okt 2004 01:33 Titel: |
 |
|
@Bruce
Ich meine es ernst, wie Du bemerkt hast:
Wenn externe Kräfte wirken oder wenn der Körper zu Beginn kinetische Energie besitzt, muss dies in einer Energiebilanz berücksichtigt werden - die entsprechende Arbeit resp. kin. Energie zeigt sich als zusätzlicher Term in der Wurzel für die Endgeschwindigkeit.
Sofern ich nur die Differenz der potentiellen Energien berechnen muss, gibt es kein Problem, weil dann ja auch keine Wurzel zu ziehen ist.
Zusammengefasst: Vorzeichen sind wichtig! Imaginäre Resultate sagen oft aus, dass der angenommen, physikalische Prozess in der klassischen Physik nicht existiert. Das Interessante ist aber, dass "imaginäre Prozesse" in der Quantenphysik mit bestimmter Wahrscheinlichkeit trotzdem passieren - finde ich faszinierend. Ein berühmtes Beispiel ist der Tunneleffekt, bei dem eine Kugel über einen Hügel rollt, obwohl die Berechnung auf dem höchsten Punkt des Hügels eine imaginäre Geschwindigkeit liefert.
Gruss
|
|
 |
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
 Bruce Verfasst am: 27. Okt 2004 11:18 Titel: Bruce Verfasst am: 27. Okt 2004 11:18 Titel: |
 |
|
O.k. maxdull,
es ist ja alles korrekt was Du sagst. Ich wollte im Fall von Para
nicht übermäßig ins Detail gehen und bin dabei wohl etwas zu sehr
in Larifari-BlaBla verfallen.
Allerdings ist Para in Mathematik noch recht unerfahren und
nun hast Du vielleicht die Aufgabe, ihm komplexe Zahlen und
den quantenmechanischen Tunneleffekt in einer für Schüler der
Klasse 11 verständlichen Form darzustellen.
Ich bin gespannt, wie Du mit den Geistern, die Du da gerufen
hast, zurecht kommst.
Gruß von Bruce
|
|
 |
Gast
|
 Gast Verfasst am: 28. Okt 2004 07:56 Titel: Gast Verfasst am: 28. Okt 2004 07:56 Titel: |
 |
|
@ Bruce, Para,
ich bin einverstanden, dass diese Geister etwas mehr Arbeit zum bändigen benötigen würden.
Nun, sie sollten Para nur etwas aufmuntern und zeigen, dass es in der Physik noch viel Interessantes zum entdecken gibt.
Maxdull
|
|
 |
|



















 .
.