| Autor |
Nachricht |
dr_fine
Anmeldungsdatum: 25.12.2008
Beiträge: 8
|
 dr_fine Verfasst am: 25. Dez 2008 20:55 Titel: Harmonische Schwingung im Lennard-Jones-Potential dr_fine Verfasst am: 25. Dez 2008 20:55 Titel: Harmonische Schwingung im Lennard-Jones-Potential |
 |
|
huhu ich hab ich ein Problem bei dem lennard-jones potential die schwingungfrequenz zu berechnen. ich schreib mal die aufgabe und das was ich bisher gemacht hab hin. ich wre über jeden hinweis oder bestätigung/kritik für das was ich gemacht habe froh. danke schonmal im voraus.
Das Lennard-Jones-Potential beschreibt die Wechselwirkung zwischen ungeladenen ungebundenen
Atomen. Es besteht aus einem anziehenden Teil, der aus van-der-Waals-Kräften und Dipol-Dipol-
Wechselwirkungen resultiert, und einem abstoßenden Teil, der aufgrund des Pauli-Prinzips eingeht.
Zusammen ergibt sich (alle Konstanten sind positiv):
=4 \cdot \varepsilon \cdot \left[\left(\frac{\sigma}{r}\right)^{12}-\left(\frac{\sigma}{r}\right)^{6}\right])
a) das lass ich mal weg
b) Bestimmen Sie das Minimum des Potentials!
dies hab ich schon gemacht und ich hab rausbekommen:

c) Entwickeln Sie das Potential in einer Taylorreihe inkl. der quadratischen Ordnung! Bestimmen
Sie außerdem die Schwingungsfrequenz, die sich daraus ergibt!
hier hab ich so meine probleme wenn ich die taylorreihe mache sieht es doch etwa so aus:
 &=& V(r_m)+\frac{\dd}{\dd r} \, V(r_m) \cdot (r-r_m)+\frac{1} {2} \cdot \frac{\dd^{2}}{\dd r^{2}} \, V(r_m) \cdot (r-r_m)^{2} \\ &=&V(r_m)+\frac{1}{2} \cdot \frac{\dd^{2}}{\dd r^{2}} \, V(r_m) \cdot (r-r_m)^{2})
aber wie komm ich den davon auf die Schwingungsfreqenz???
d)das lass ich auch mal weg
Für Argon sind die Parameter gegeben durch  und und 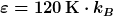
e) Bei welchem Abstand liegt für Argon das Minimum des Potentials? Wie groß ist die Schwingungsfrequenz?
hier müsste man ja lediglich sigma in die gleichung für minimums einsetzten und erhielte den Radius im minimum:


auch gut aber die schwingungfreqenz kann hier nun auch wieder nicht berechnen |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 26. Dez 2008 13:13 Titel: Re: Lennard-Jones Potential as_string Verfasst am: 26. Dez 2008 13:13 Titel: Re: Lennard-Jones Potential |
 |
|
| dr_fine hat Folgendes geschrieben: | | aber wie komm ich den davon auf die Schwingungsfreqenz??? |
Bei so einem Potential ist ja der konstante Teil (zumindest für die Schwingung) egal. Man könnte ja bei einem Potential immer eine Konstante dran addieren und hätte dann immer noch die selben Bewegungsgleichungen.
Der lineare Teil fällt weg, weil er bei einem Minimum ja immer 0 sein muss (hast Du ja auch schon so geschreiben).
Bleibt also nur noch der quadratische Term. Wenn Du Dich an einen harmonischen Oszillator zurück erinnerst, gibt es dort auch nur einen quadratischen Anteil. Wenn die Ausschläge um das Minimum herum also klein sind und deshalb die Taylor-Reihe bis dahin die Funktion genau genug abbildet, kannst Du immer von einer harmonischen Schwingung in dieser Näherung ausgehen. Das macht harmonische Schwingungen besonders wichtig, weil die in der ersten Näherung bei kleinen Ausschlägen immer ganz gut stimmen und weil man dafür auch eine Lösung kennt. Aus der Lösung eines harmonischen Oszillators, bei dem auch die Frequenz bekannt ist, kannst Du hier auch eine Frequenz bestimmen. Deshalb: Wie sieht ein harmonischen Potential aus? Vergleiche das (besonders die Konstanten) mit dem quadratischen Teil der Taylor-Reihe des LJ-Potentials. Damit kannst Du sehen, welche Konstanten sich entsprechen und damit auch die Schwingungsfrequenz Dir überlegen, indem Du die Lösung für das harmonische Potential nimmst.
Alternativ könntest Du genau wie beim harmonischen Oszillator die Differentialgleichung für die Bewegung aufstellen und die dann lösen. Aber das ist ja genau das selbe, wie auch schon beim harmonischen Oszillator, weshalb Du einfach die Lösung verwenden kannst.
Gruß
Marco |
|
 |
dr_fine
Anmeldungsdatum: 25.12.2008
Beiträge: 8
|
 dr_fine Verfasst am: 28. Dez 2008 17:05 Titel: dr_fine Verfasst am: 28. Dez 2008 17:05 Titel: |
 |
|
ja genau das hab ich mir auch gedacht dass nur der quadratische therm über bleibt.
also bei einer harmonischen schwingung, bei einem federpendel zb hab ich ja

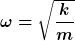

wobei k die federkonstante is und gleichzeitig die zweite ableitung von potential ist:


kann man dann auch sagen dass die zweite ableitung des LJ Potentials dem k entspricht und sagen:

also:
*\frac{1}{m}})
*\frac{1}{m}}*\frac{1}{2*\pi})
so in etwa? |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 28. Dez 2008 17:18 Titel: as_string Verfasst am: 28. Dez 2008 17:18 Titel: |
 |
|
Hallo!
Ich hab's jetzt wirklich nur ganz kurz überflogen, aber es erscheint mir richtig zu sein. Für die ganzen Konstanten kann ich jetzt aber keine Hand ins Feuer legen, aber das Prinzip ist richtig, mE.
Gruß
Marco |
|
 |
dr_fine
Anmeldungsdatum: 25.12.2008
Beiträge: 8
|
 dr_fine Verfasst am: 28. Dez 2008 18:11 Titel: dr_fine Verfasst am: 28. Dez 2008 18:11 Titel: |
 |
|
ok das ist doch mal gut, vielen dank
ich hab für ein argon atom jetzt etwa 3 Terahz als schwingungsfreqenz rausbekommen kann das größenordungsmäßig sein? |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 28. Dez 2008 21:38 Titel: as_string Verfasst am: 28. Dez 2008 21:38 Titel: |
 |
|
Die Größenordnung sieht mir ok aus. So weit ich weiß, sind solche Schwingungsfrequenzen im THz Bereich. Aber ich werde es bei Gelegenheit mal noch nachrechnen, denke ich.
Gruß
Marco |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 29. Dez 2008 13:10 Titel: as_string Verfasst am: 29. Dez 2008 13:10 Titel: |
 |
|
Hallo!
Ich habe jetzt auch mal eine Weile rumgerechnet. Ich komme allerdings auf ein etwas anderes Ergebnis (was aber durchaus falsch sein kann...):
Ich habe für 2·V''(rm):
 = \frac{12^2}{\sqrt[3]{2}}\frac{\varepsilon}{\sigma^2})
Dann würde mein

Und wenn ich daraus die Frequenz ausrechne, dann habe ich:

Mmh... Ich muss das mal noch nachprüfen. Mit den Konstanten bin ich mir komplett unsicher. Außerdem könnte man mal schauen, ob man für die Schwingungsfrequenz nicht auch einen echten Wert im Internet finden kann. Zumindest um die Größenordnung zu bestätigen.
Gruß
Marco |
|
 |
dr_fine
Anmeldungsdatum: 25.12.2008
Beiträge: 8
|
 dr_fine Verfasst am: 30. Dez 2008 14:23 Titel: dr_fine Verfasst am: 30. Dez 2008 14:23 Titel: |
 |
|
1.was hast du als epsilon genommen?
bin mir da nicht so sicher was das k_B in der aufgabenstellung bedeutet, ich habe 1,2*10^-21J als epsilon genommen, bin aber nicht so sicher ob das richtig ist.
2. | Zitat: |  = \frac{12^2}{\sqrt[3]{2}}\frac{\varepsilon}{\sigma^2}) |
da hab ich nicht mal 2 genommen. sondern ) gesetzt gesetzt |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 30. Dez 2008 14:55 Titel: as_string Verfasst am: 30. Dez 2008 14:55 Titel: |
 |
|
| dr_fine hat Folgendes geschrieben: | | 1.was hast du als epsilon genommen? |
Ich habe das hier genommen:
http://www.google.de/search?q=120K%2Aboltzmann+constant
Wie kommst Du auf Dein Ergebnis?
| dr_fine hat Folgendes geschrieben: | 2. | Zitat: |  = \frac{12^2}{\sqrt[3]{2}}\frac{\varepsilon}{\sigma^2}) |
da hab ich nicht mal 2 genommen. sondern ) gesetzt gesetzt |
Kann sein, dass ich das die ½ aus der Taylor-Entwicklung vergessen habe. Wahrscheinlich hast Du recht, dass da kein Faktor von 2 rein kommt. Ich muss das nochmal überprüfen.
Gruß
Marco |
|
 |
dr_fine
Anmeldungsdatum: 25.12.2008
Beiträge: 8
|
 dr_fine Verfasst am: 30. Dez 2008 15:25 Titel: dr_fine Verfasst am: 30. Dez 2008 15:25 Titel: |
 |
|
also is schonmal gut zu wissen dass das die boltzman konstante ist 
naja mein wert is dann falsch (hab irgendwo im internet gefunden das das epsilon in der gößenordung von 10^-21 sein muss da hab ich es einfach übernommen)
mit der 2 dadrin bin ich mir auch nicht so sicher ob man die braucht oder nicht. wo nimmst du die denn her?
mit der zwei erhält man dein berechnetes ergebnis 0,79 THz
und ohne erhält man 0,559THz
ich habe bisher noch kein gesichertes ergebnis dafür gefunden,womit man überprüfen kann welches eher hinhaut. |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 30. Dez 2008 16:20 Titel: as_string Verfasst am: 30. Dez 2008 16:20 Titel: |
 |
|
| dr_fine hat Folgendes geschrieben: | also is schonmal gut zu wissen dass das die boltzman konstante ist  |
Ja, das müsste schon die Boltzmann-Konstante sein. Für die schreibt man häufig kb. Außerdem stimmt die Größenordnung dann auch und es soll ja außerdem eine Energie herauskommen. Man kann Kelvin auf diese Art quasi als eine Energieeinheit auffassen mit dem Umrechnungsfaktor kb einfach.
| dr_fine hat Folgendes geschrieben: | | mit der 2 dadrin bin ich mir auch nicht so sicher ob man die braucht oder nicht. wo nimmst du die denn her? |
Ich denke, die ist falsch. Ich bin ausgegangen von V=½kx² und hatte gedacht, dass für die Entwicklung des LJ-Potentials einfach V''(r_m)·delta r² raus käme. Dann hätte ich eben V'' = ½k und dann den Faktor 2 drin. Das ist aber nicht richtig, weil bei der Taylor-Entwicklung ja auch ein Faktor von ½ drin steht, den ich vergessen hatte. Deshalb müsste eigentlich k=V''(r_m) sein.
| dr_fine hat Folgendes geschrieben: | mit der zwei erhält man dein berechnetes ergebnis 0,79 THz
und ohne erhält man 0,559THz |
Genau, das habe ich auch. Die 0,558THz wären dann mein Ergebnis. Ich bin mir aber bei der ganzen Rumrechnerei nicht so sicher, dass das mit der 12² und so weiter alles stimmt. Ich bin irgendwie auch zu faul, das jetzt nochmal nach zu rechnen...
| dr_fine hat Folgendes geschrieben: | | ich habe bisher noch kein gesichertes ergebnis dafür gefunden,womit man überprüfen kann welches eher hinhaut. |
Ich hatte auch kurz geschaut und auf die Schnelle zumindest nichts gefunden. Mmh, keine Ahnung, wie man da am einfachsten/schnellst Werte bekommen kann. Zumindest eine grobe Größenordnung wäre erstmal ja schon hilfreich. Das würde dann zwar noch nicht unbedingt helfen, zwischen den beiden Ergebnissen zu unterscheiden, aber wenigstens zeigen, ob wir in etwa im richtigen Bereich liegen.
Gruß
Marco
PS: Wenn Du irgendwann das Ergebnis haben würdest, würde mich das natürlich sehr interessieren! Aber vom Prinzip her ist es schon richtig (also der Lösungsweg) und Rechenfehler sind zwar ärgerlich, aber vielleicht auch nicht so wahnsinnig wichtig. |
|
 |
dr_fine
Anmeldungsdatum: 25.12.2008
Beiträge: 8
|
 dr_fine Verfasst am: 30. Dez 2008 16:35 Titel: dr_fine Verfasst am: 30. Dez 2008 16:35 Titel: |
 |
|
ja das passt schon
ergebnis kann noch etwas dauern bis ich das habe, so 8 jan oder so,lass ich dir zukommen
vielen vielen dank nochmal |
|
 |
Suppenmax
Anmeldungsdatum: 03.01.2009
Beiträge: 2
|
 Suppenmax Verfasst am: 03. Jan 2009 15:39 Titel: Suppenmax Verfasst am: 03. Jan 2009 15:39 Titel: |
 |
|
Hallo! Ich hätte mal eine Frage.
Warum taylort man in dem Minimum der Funktion und nicht in der Nullstelle  ? Ich habe mir das so vorgestellt, dass der Abstand, in dem das Potential Null ist, die Ruhelage der Oszillation ist. Wenn nein, warum nicht? Was bedeutet dieses Minimum wo ihr aproximiert habt? Es ist doch eigentlich der Punkt, wo die auslenkung in die negative Richtung maximal ist, oder? ? Ich habe mir das so vorgestellt, dass der Abstand, in dem das Potential Null ist, die Ruhelage der Oszillation ist. Wenn nein, warum nicht? Was bedeutet dieses Minimum wo ihr aproximiert habt? Es ist doch eigentlich der Punkt, wo die auslenkung in die negative Richtung maximal ist, oder? |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 03. Jan 2009 15:57 Titel: as_string Verfasst am: 03. Jan 2009 15:57 Titel: |
 |
|
| Suppenmax hat Folgendes geschrieben: | | Ich habe mir das so vorgestellt, dass der Abstand, in dem das Potential Null ist, die Ruhelage der Oszillation ist. Wenn nein, warum nicht? Was bedeutet dieses Minimum wo ihr aproximiert habt? Es ist doch eigentlich der Punkt, wo die auslenkung in die negative Richtung maximal ist, oder? |
Nein, das ist der Punkt, an dem der Körper kräftefrei ist. Vom Potential kommt man auf die Kraft, indem man den Gradienten bildet, im eindimensionalen also einfach die Ableitung. Und da wo ein Minimum ist, ist die Ableitung 0, also ist es dort kräftefrei.
Stell Dir doch einfach ein Höhenprofil vor. Da bleibt eine Kugel auf im tiefsten Punkt liegen und nicht irgendwo, wo man zufällig gesagt hat, dass das Potential 0 sein soll. Den absoluten Wert kann man doch beliebig festlegen. Man könnte genau so gut ein Potential nehmen, bei dem man noch einen konstanten Wert dazu addiert hat.
Was mir aber noch zur Schwingungsfrequenz eingefallen ist: Die beiden Atome haben in unserem Bsp. ja die selbe Masse. Wir haben aber angenommen, dass ein Körper im ortsfesten Potential des anderen schwingt. Das ist aber nicht so ganz richtig, weil der andere sich ja genau so bewegt und damit das Potential auch nicht ortsfest ist. Eigentlich ist das nämlich ein Zweikörper-Problem. Und da würde man eher die "reduzierte Masse" dann nehmen müssen, was in unserem Bsp. doch wieder ein Faktor von ½ irgendwo rein bringen müsste.
Gruß
Marco |
|
 |
Suppenmax
Anmeldungsdatum: 03.01.2009
Beiträge: 2
|
 Suppenmax Verfasst am: 03. Jan 2009 20:55 Titel: Suppenmax Verfasst am: 03. Jan 2009 20:55 Titel: |
 |
|
Danke!
| Zitat: | c) Entwickeln Sie das Potential in einer Taylorreihe inkl. der quadratischen Ordnung! Bestimmen
Sie außerdem die Schwingungsfrequenz, die sich daraus ergibt! |
Man braucht doch eigentlich gar nicht die Taylorreihe, um auf die Schwingungsfrequenz zu schließen, oder? Man muss doch um k zu bestimmen nur die die zweite Ableitung des Potentials im punkt des Minimums kennen. Warum dann der Aufwand mit der Taylorreihung? |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 04. Jan 2009 00:19 Titel: as_string Verfasst am: 04. Jan 2009 00:19 Titel: |
 |
|
| Suppenmax hat Folgendes geschrieben: | | Man braucht doch eigentlich gar nicht die Taylorreihe, um auf die Schwingungsfrequenz zu schließen, oder? Man muss doch um k zu bestimmen nur die die zweite Ableitung des Potentials im punkt des Minimums kennen. Warum dann der Aufwand mit der Taylorreihung? |
Das ist doch das selbe. Man weiß schon, dass die erste Ableitung 0 sein wird und dass der konstante Term keine Rolle spielt. Also läuft die Taylorreihe bis zur zweiten Ordnung doch gerade darauf raus.
Die Sache ist doch zu verstehen, dass ein Potential immer dann, wenn es ein Minimum hat, in dieser Art behandelt werden kann. Wenn die Ausschläge klein sind um das Minimum herum, dann kann man für ein solches eben die harmonische Näherung verwenden. Aber um das zu verstehen, muss man ja schon mit der Taylorentwicklung argumentieren. Sonst kommt man ja nicht unbedingt a priori darauf, dass die Frequenz überhaupt etwas mit der zweiten Ableitung zu tun hat.
Außerdem kommt da ja auch noch der Faktor ½ dazu, den ich oben vergessen hatte, der aber aus der Taylorreihe direkt folgt.
Dann kann man dieses Prinzip auch noch weiter verfolgen und z. B. versuchen zu der harmonischen Lösung noch die dritte Ordnung als "Störterm" oder Störpotential aufzufassen und mit der Störungsrechnung das dann auch noch mit zu berücksichtigen.
Ich wüsste zumindest jetzt nicht, wie ich begründen sollte, dass die Lösung für das harmonische Potential auch in erster Näherung die Lösung für eine kleine Schwingung in einem beliebigen Potential mit einem Minimum sein muss, ohne mit der Taylorreihe zu argumentieren. Und warum das k des harmonischen Potentials dann gerade der zweiten Ableitung an dieser Stelle entspricht, wird mir auch erst mit der Taylorreihe klar. Oder hast Du da eine direktere Erklärung dafür?
Gruß
Marco |
|
 |
Henri
Anmeldungsdatum: 08.02.2014
Beiträge: 82
|
 Henri Verfasst am: 03. Jan 2017 20:40 Titel: Henri Verfasst am: 03. Jan 2017 20:40 Titel: |
 |
|
Servus,
ich grabe das mal aus, weil ich dazu eine kurze Frage habe:
| dr_fine hat Folgendes geschrieben: |
wobei k die federkonstante is und gleichzeitig die zweite ableitung von potential ist:
 |
Vielleicht eine blöde Frage aber woher weiß man dass die Federkonstante die zweite Ableitung des Potentials ist? Das höre ich zum ersten Mal, aber wenn ich mir das herleiten könnte wäre es sehr hilfreich 
Viele Grüße |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 03. Jan 2017 20:44 Titel: jh8979 Verfasst am: 03. Jan 2017 20:44 Titel: |
 |
|
|
Leite mal V_F zweimal ab. |
|
 |
Henri
Anmeldungsdatum: 08.02.2014
Beiträge: 82
|
 Henri Verfasst am: 04. Jan 2017 12:31 Titel: Henri Verfasst am: 04. Jan 2017 12:31 Titel: |
 |
|
Ups  |
|
 |
|

















