| Autor |
Nachricht |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 07. Feb 2018 15:10 Titel: Resonanzfrequenz einer gedämpften Schwingung. itscool123 Verfasst am: 07. Feb 2018 15:10 Titel: Resonanzfrequenz einer gedämpften Schwingung. |
 |
|
Hallo ich benötige hilfe bei folgender Aufgabenstellung:
Eine Masse m = 12,5g führt an zwei parallel wirkenden Federn D1=500N/m, D2=1,5kN/m eine gedämpfte Schwingung aus, wenn sie durch einen Stoß ausgelenkt wird. Über viskose Reibung Fr=k*v erfolgt eine Dämpfung der Schwingung. Die Resonanzfrequenz des gedämpften Systems beträgt 65,66 Hz
a. Wie groß ist die Gesamtfederkonstante D?
b. Wie groß ist die Reibungskonstante k=2*s/m wenn sich die Schwingungsamplitude zwischen 3 Maxima Halbiert?
c. Wie groß ist die Resonanzfrequenz der ungedämpften Schwingung?
d. Skizzieren sie den Verlauf der ersten 3 Schwingungen
e Durch Kurzschluss der Schwingspule kann das System in den aperiodischen Grenzfall überführt werden. Um welchen Faktor muss die Reibungskonstante k dazu erhöht werden ?
Ich brauche zu allen Teilaufgaben Hilfe 
Erstmal zur a.)
Die resonanzfrequenz sollte mir eigentlich informationen über die Amplitude geben, oder? Denn da sollte die Amplitude doch am höchsten sein ? " Ist die Erregerfrequenz gleich der Eigenfrequenz des Schwingers, so erreicht die Amplitude der Schwingung ein Maximum. Das wird als Resonanz bezeichnet. "
Also wollte ich für die Eigenfrequenz die ich für die Formel 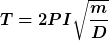 benötige berechnen, da ich sie für T brauche. Nur weiß ich nicht wie ich auf diese komme. Gibt es eine Formel dazu die ich nicht finde ? benötige berechnen, da ich sie für T brauche. Nur weiß ich nicht wie ich auf diese komme. Gibt es eine Formel dazu die ich nicht finde ?
Würde mich um Hife freuen 
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 07. Feb 2018 15:29 Titel: Steffen Bühler Verfasst am: 07. Feb 2018 15:29 Titel: |
 |
|
Was die a betrifft, sollst Du lediglich die Federkonstante der Parallelschaltung D1||D2 berechnen.
Viele Grüße
Steffen
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 07. Feb 2018 19:44 Titel: itscool123 Verfasst am: 07. Feb 2018 19:44 Titel: |
 |
|
|
Also einfach D1+D2?
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 07. Feb 2018 19:56 Titel: Myon Verfasst am: 07. Feb 2018 19:56 Titel: |
 |
|
|
Ja, D=D1+D2.
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 08. Feb 2018 14:26 Titel: itscool123 Verfasst am: 08. Feb 2018 14:26 Titel: |
 |
|
Keine Ahnung warum ich nicht daran gedacht habe. Jedenfalls ist die Federkonstante somit 2kN/m.
Und zur b.)
Also ist die Reibungskonstante so groß dass sich die Amplituden nach 3 Perioden sich Halbiert? Also ist die reibungskonstante 2/3=0,6?
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 08. Feb 2018 14:31 Titel: itscool123 Verfasst am: 08. Feb 2018 14:31 Titel: |
 |
|
|
ich meine 1/2:3=0,16 ist die konstante nicht 0,6
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 08. Feb 2018 14:57 Titel: Steffen Bühler Verfasst am: 08. Feb 2018 14:57 Titel: |
 |
|
Nein, so einfach ist das dann auch nicht.
Die Reibungskonstante k ist laut Aufgabe ja eine Größe, die mit der Geschwindigkeit multipliziert die Reibungskraft ergibt (Fr=k*v). Sie kann also nicht dimensionslos sein.
Vielmehr entspricht sie dem d in der hier beschriebenen Differentialgleichung. Und weiter unten wird dort auch die Lösung für den Schwingfall gezeigt: eine Sinusschwingung, die mit 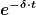 abklingt, mit abklingt, mit 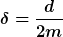
Und dieses Abklingen hilft uns weiter! Wir brauchen nun die Zeit vom ersten Maximum bis zum dritten Maximum, die ist ja bekannt. Diese setzen wir in den Exponentialterm ein. Wenn die Schwingung in dieser Zeit auf die Hälfte abgeklungen ist, muss der also welche Zahl ergeben? Genau. Und nun nach  auflösen und d (das ist das gesuchte k) bestimmen. auflösen und d (das ist das gesuchte k) bestimmen.
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 08. Feb 2018 16:08 Titel: itscool123 Verfasst am: 08. Feb 2018 16:08 Titel: |
 |
|
T = 2PI ·√ m/D
Für die Zeit fällt mir nur die Periodendauer ein und für diese habe ich ja alles....
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 08. Feb 2018 16:11 Titel: Steffen Bühler Verfasst am: 08. Feb 2018 16:11 Titel: |
 |
|
| itscool123 hat Folgendes geschrieben: | | T = 2PI ·√ m/D |
Diese Formel ist hier nicht von Belang. Die gilt nur im ungedämpften Zustand. Für c kannst Du sie also schon mal im Kopf behalten.
| itscool123 hat Folgendes geschrieben: | | Für die Zeit fällt mir nur die Periodendauer ein |
Genau, aber eben die vom aktuellen, also gedämpften System. Die ist ja über die genannte Resonanzfrequenz bekannt. Wie lang dauert es also vom ersten Maximum bis zum dritten?
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 08. Feb 2018 20:18 Titel: itscool123 Verfasst am: 08. Feb 2018 20:18 Titel: |
 |
|
| itscool123 hat Folgendes geschrieben: | | Für die Zeit fällt mir nur die Periodendauer ein |
Genau, aber eben die vom aktuellen, also gedämpften System. Die ist ja über die genannte Resonanzfrequenz bekannt. Wie lang dauert es also vom ersten Maximum bis zum dritten?[/quote]
mhhh Ich weiß nicht wie ich auf eine Zeit Angabe kommen kann.
Ich verstehe auch nicht was die Resonanzfrequenz so ganz ist.
Ich weiß was Resonanz ist, aber die Frequenz nicht. Resonanz ist wenn die zugeführte energie genau so groß ist wie energie des systems?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 08. Feb 2018 21:15 Titel: Re: Resonanzfrequenz einer gedämpften Schwingung. Steffen Bühler Verfasst am: 08. Feb 2018 21:15 Titel: Re: Resonanzfrequenz einer gedämpften Schwingung. |
 |
|
Laut Aufgabe führt die Masse
| Zitat: | eine gedämpfte Schwingung aus, wenn sie durch einen Stoß ausgelenkt wird.
...
Die Resonanzfrequenz des gedämpften Systems beträgt 65,66 Hz. |
Das ist wie immer: man haut irgendwo drauf, und es macht dong. Und zwar mit der Resonanzfrequenz. Ein abklingender Cosinus ebendieser Frequenz. Zeichne ihn Dir ruhig mal hin (sollst Du ja auch für d). Geht mit dem ersten Maximum los, runter, rauf zum zweiten, runter, rauf zum dritten. Dann ist nur noch die Hälfte vom ersten da.
Jetzt?
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 09. Feb 2018 11:29 Titel: Steffen Bühler Verfasst am: 09. Feb 2018 11:29 Titel: |
 |
|
Nein.
Das erste Maximum des Cosinus liegt bei Null.
Das zweite Maximum des Cosinus liegt bei 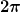 , also nach einer Periode. , also nach einer Periode.
Das dritte Maximum des Cosinus liegt bei 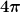 , also nach zwei Perioden. , also nach zwei Perioden.
Zwischen diesen drei Maxima liegen also zwei Perioden.
Zwischen diesen drei Maxima halbiert sich die Schwingungsamplitude.
Nun wissen wir, dass die Frequenz unserer Schwingung 65,66 Hz ist.
Wie lang ist also die Periode?
Wie lang sind also zwei Perioden?
Innerhalb welcher Zeit halbiert sich also die Schwingungsamplitude?
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 09. Feb 2018 12:13 Titel: itscool123 Verfasst am: 09. Feb 2018 12:13 Titel: |
 |
|
Wie lang ist also die Periode?
Wie du gesagt hast, 2PI.
Wie lang sind also zwei Perioden?
4PI
Innerhalb welcher Zeit halbiert sich also die Schwingungsamplitude?
Innerhalb der 4PI
Warum betrachten wir eigentlich den Cosinus?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 09. Feb 2018 12:35 Titel: Steffen Bühler Verfasst am: 09. Feb 2018 12:35 Titel: |
 |
|
Ich will aber wissen, innerhalb wieviel Sekunden sich die Amplitude halbiert. Wie lang ist denn die Periode der Schwingung in Sekunden?
Den Cosinus habe ich genommen, weil der hier von der Anschauung besser passt: das System wird zum Zeitpunkt Null angestoßen und hat da also gleich das erste Maximum. Den Sinus kannst Du zur Berechnung aber natürlich genauso nehmen.
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 09. Feb 2018 13:16 Titel: itscool123 Verfasst am: 09. Feb 2018 13:16 Titel: |
 |
|
Och man ich bin richtig blöd.
Hab vergessen dass, Hertz 1/s ist und auch eine Zeit ist... das sind dann 0,0157s für 63,66. In der Aufgabenstellung steht 65,33 das habe ich falsch aus der Aufgabenstellung bei mir übernommen. Also 63,33 Hertz
Also ist T=0,0157s
Also halbiert sich die Amplitude nach 3*T = 0,047s
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 09. Feb 2018 13:22 Titel: Steffen Bühler Verfasst am: 09. Feb 2018 13:22 Titel: |
 |
|
Nein, eben nicht nach 3T, sondern, e nun schon mehrfach von Dir und mir geschrieben...
Eine Periode liegt zwischen zwei Maxima, wieviel Perioden liegen zwischen drei Maxima?
Wenn Du das hast, kannst Du  berechnen. Was hast Du da raus? Was ergibt sich dann für die Reibungskonstante? berechnen. Was hast Du da raus? Was ergibt sich dann für die Reibungskonstante?
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 09. Feb 2018 13:53 Titel: itscool123 Verfasst am: 09. Feb 2018 13:53 Titel: |
 |
|
Nach 2 Perioden..
also dann 2*T= 0,0315s
also e^-d/m*t=s (abklkingungs ding)
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 09. Feb 2018 13:55 Titel: Steffen Bühler Verfasst am: 09. Feb 2018 13:55 Titel: |
 |
|
|
Richtig. Was ergibt sich dann für die Reibungskonstante?
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 09. Feb 2018 14:37 Titel: itscool123 Verfasst am: 09. Feb 2018 14:37 Titel: |
 |
|
Hab aber zwei Variablen in meiner Gleichung?
ln(-d/m*t)=s
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 09. Feb 2018 14:58 Titel: Steffen Bühler Verfasst am: 09. Feb 2018 14:58 Titel: |
 |
|
Dieses s sagt mir nichts, ich kenne Eure Formelsammlung nicht.
Aber ich ja weiter oben geschrieben habe, geht es jetzt darum, dass die Amplitude in der Zeit von Null bis 2T auf die Hälfte gesunken ist.
Also von 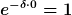 auf auf 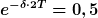 . .
Wie gesagt: setz ein, löse nach  auf und berechne die Reibungskonstante auf und berechne die Reibungskonstante 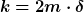 . Dann hast Du's. . Dann hast Du's.
Oder verrate mir, was s sein soll.
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 09. Feb 2018 15:52 Titel: Steffen Bühler Verfasst am: 09. Feb 2018 15:52 Titel: |
 |
|
Ich hab die Formeln aus dem genannten Wiki-Link.
Aber dann nehmen wir die aus Deiner Formelsammlung. Ab Seite 44 wird das dort erklärt. Die Reibungskonstante heißt in der Aufgabe k, bei Wiki d, und hier nun b. Als ich studiert habe, wurde sie übrigens R genannt.
[offtopic]
Das ist etwas, was ich den Physikdozenten dieser Welt bis heute ankreide: eigentlich ist das Thema gar nicht so schwer, aber wenn man die Studenten mit derart viel Durcheinander verwirrt, braucht man sich nicht zu wundern, wenn es Schwierigkeiten gibt.
[/]
Der Abklingkoeffizient heißt hier aber zum Glück ebenfalls 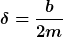 . Dann passt es wunderbar, lös mal auf. . Dann passt es wunderbar, lös mal auf.
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 09. Feb 2018 16:53 Titel: itscool123 Verfasst am: 09. Feb 2018 16:53 Titel: |
 |
|
| Steffen Bühler hat Folgendes geschrieben: |
Also von 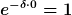 auf auf 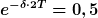 . .
Wie gesagt: setz ein, löse nach  auf und berechne die Reibungskonstante auf und berechne die Reibungskonstante 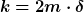 . Dann hast Du's. . Dann hast Du's.
Oder verrate mir, was s sein soll. |
wie bist du denn darauf gekommen dass das =0,5 ist ? und kommt dieses e^-s(abklingkoeffizient)*t von dem hier vielleicht :
=x_{0}\cdot e^{-\delta \cdot t} \cdot cos(w\cdot t+\varphi ))
seite 45 ganz oben die gleichung
Jedenfalls kommt dort dann für den Abklingkoeffizient 2,07 raus laut deiner Formel. Und für k=0,125kg*2,07=0,258?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 09. Feb 2018 17:10 Titel: Steffen Bühler Verfasst am: 09. Feb 2018 17:10 Titel: |
 |
|
Das mit der 0,5 hatte ich vorher mit einigen Zaunpfählen versucht, Dir klarzumachen. Es liegt in der Tat an der Gleichung, die Du abgeschrieben hast.
Wir haben doch eine Schwingung, bei der die Amplitude exponentiell kleiner wird. Wie schnell sie kleiner wird, beschreibt eben dieser Abklingkoeffizient  . Wenn man den nicht kennt, schaut man eben, nach welcher Zeit die Amplitude auf z.B. die Hälfte gegangen ist (das nennt man übrigens deswegen Halbwertzeit), dann muss man . Wenn man den nicht kennt, schaut man eben, nach welcher Zeit die Amplitude auf z.B. die Hälfte gegangen ist (das nennt man übrigens deswegen Halbwertzeit), dann muss man 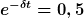 nach nach  auflösen, wie hier. Man muss nicht unbedingt die Hälfte nehmen, wenn man ein Zehntel nimmt, geht's zum Beispiel auch: auflösen, wie hier. Man muss nicht unbedingt die Hälfte nehmen, wenn man ein Zehntel nimmt, geht's zum Beispiel auch: 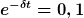
Beim Auflösen ist Dir aber irgendwas durcheinandergeraten. Rechne noch mal langsam:
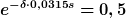
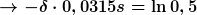
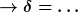
Die Einheit nicht vergessen. Und dann die richtige Masse für die Reibungszahl! Deine 0,125kg sind eigenartig.
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 09. Feb 2018 17:21 Titel: itscool123 Verfasst am: 09. Feb 2018 17:21 Titel: |
 |
|
ACHSO DIE HÄLFTE DER ZEIT DESWEGEN DIE 0,5
DU GENIE ICH MAG DICH VOLL
stimmt meine 0,125kg sind falsch 0,0125kg dann
Für den Abklingkoeffizienten dann =22?
und für k=2*22= 44
Was ist denn mit dem rest der Funktion passiert ? die cos(w*t+phi) usw?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 09. Feb 2018 17:44 Titel: Steffen Bühler Verfasst am: 09. Feb 2018 17:44 Titel: |
 |
|
| itscool123 hat Folgendes geschrieben: | | stimmt meine 0,125kg sind falsch 0,0125kg dann |
Richtig, das ist die Masse m.
| itscool123 hat Folgendes geschrieben: | | Für den Abklingkoeffizienten dann =22? |
Der Zahlenwert stimmt. Ich glaube, ich hatte was von "Einheit" geschrieben. Also?
| itscool123 hat Folgendes geschrieben: | | für k=2*22= 44 |
Das ist aber nicht streng nach der Formel 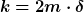 , oder? , oder?
| itscool123 hat Folgendes geschrieben: | | Was ist denn mit dem rest der Funktion passiert? |
Das ist eben die eigentliche Schwingung, das "dong". Ein Cosinus mit einer Frequenz und einer Phasenverschiebung. Die Frequenz ist unsere Resonanzfrequenz, die Phasenverschiebung ist hier unbekannt, ist für die Rechnung aber auch egal. Durch die e-Funktion davor klingt diese Schwingung ab. Und nur dieses Abklingen interessiert hier.
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 09. Feb 2018 17:57 Titel: itscool123 Verfasst am: 09. Feb 2018 17:57 Titel: |
 |
|
achsooo K=2*s/m
Ich weiß auch nicht warum ich dachte das dass meter oder irgendeine Einheit wäre, jesus.
ALSO:
laut deiner formel k=2*m*abklingkoeffizient =2*0,0125kg*22=0,55
In meiner Aufgabenstellung steht aber irgendwie k=2*abklingkoeffizient/m?
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 09. Feb 2018 18:00 Titel: itscool123 Verfasst am: 09. Feb 2018 18:00 Titel: |
 |
|
hier mal die aufgabe
| Beschreibung: |
|

Download |
| Dateiname: |
cool123.png |
| Dateigröße: |
60.43 KB |
| Heruntergeladen: |
346 mal |
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 09. Feb 2018 18:07 Titel: Steffen Bühler Verfasst am: 09. Feb 2018 18:07 Titel: |
 |
|
| itscool123 hat Folgendes geschrieben: | | k=2*m*abklingkoeffizient =2*0,0125kg*22=0,55 |
Gut, wenn Du's nicht tust, muss ich Dir halt die Einheiten hinschreiben:

Denn  hat die Einheit hat die Einheit 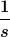 , Du hast ja durch eine Zeit geteilt, um es zu bestimmen. Sonst würde auch , Du hast ja durch eine Zeit geteilt, um es zu bestimmen. Sonst würde auch 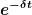 gar nicht funktionieren, denn die e-Funktion kann nur mit Zahlen was anfangen. Und nur so heben sich die Einheiten gegenseitig auf. gar nicht funktionieren, denn die e-Funktion kann nur mit Zahlen was anfangen. Und nur so heben sich die Einheiten gegenseitig auf.
| itscool123 hat Folgendes geschrieben: | | In meiner Aufgabenstellung steht aber irgendwie k=2*abklingkoeffizient/m? |
Ja, hab ich gesehen. Sehr diffus. Meine Meinung über Physikdozenten hab ich ja schon mitgeteilt.
So, ich hab jetzt meinen Schachabend. Bis demnächst!
Viele Grüße
Steffen
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 09. Feb 2018 18:18 Titel: itscool123 Verfasst am: 09. Feb 2018 18:18 Titel: |
 |
|
Ich bedanke mich sehr!!! Und viel spaß beim Schachabend!!!

|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 16. Feb 2018 13:05 Titel: itscool123 Verfasst am: 16. Feb 2018 13:05 Titel: |
 |
|
|
Wie berechne ich denn jetzt die Resonanzfrequenz der ungedämpften schwingung aus?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 16. Feb 2018 13:32 Titel: Steffen Bühler Verfasst am: 16. Feb 2018 13:32 Titel: |
 |
|
Wie immer über 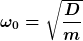 . .
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 17. Feb 2018 16:05 Titel: itscool123 Verfasst am: 17. Feb 2018 16:05 Titel: |
 |
|
|
die winkelgeschwindigkeit am anfang ist die resoannz ? oder warum?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 17. Feb 2018 16:11 Titel: Steffen Bühler Verfasst am: 17. Feb 2018 16:11 Titel: |
 |
|
|
Wegen der Null? Nein, das ist allgemein die Abkürzung für die Resonanzfrequenz ohne Dämpfung. Steht auch in Deiner Formelsammlung.
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 17. Feb 2018 16:20 Titel: itscool123 Verfasst am: 17. Feb 2018 16:20 Titel: |
 |
|
Die Resonanzfrequenz einer ungedämpften Schwingung entspricht der Kreisfrequenz? Warum?
Wie würde man die Resonanzfrequenz einer gedämpften Schwingung denn berechnen?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 17. Feb 2018 16:31 Titel: Steffen Bühler Verfasst am: 17. Feb 2018 16:31 Titel: |
 |
|
Auch das steht in Deiner Formelsammlung: 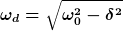
Sie ist also grundsätzlich kleiner als die Eigenkreisfrequenz. Und wenn die Dämpfung  gerade so groß ist, dass gerade so groß ist, dass 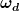 auf Null geht, haben wir den aperiodischen Grenzfall. auf Null geht, haben wir den aperiodischen Grenzfall.
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 17. Feb 2018 16:59 Titel: itscool123 Verfasst am: 17. Feb 2018 16:59 Titel: |
 |
|
Bei uns wurde komischer weise diese Formel benutzt:
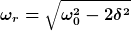
die finde ich nicht in meiner formelsammlung. Wo für ist die ?
|
|
 |
itscool123
Anmeldungsdatum: 25.01.2018
Beiträge: 73
|
 itscool123 Verfasst am: 17. Feb 2018 17:04 Titel: itscool123 Verfasst am: 17. Feb 2018 17:04 Titel: |
 |
|
|
Okay ich habe sie doch gefunden aber jetzt bin ich verwirrt. Da in der Aufgabe steht dass man die Resonanzfrequenz ohne Dämpfung berechnet aber in der Formel wird die Dämpfung berücksichtigt ?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7295
|
 Steffen Bühler Verfasst am: 17. Feb 2018 19:08 Titel: Steffen Bühler Verfasst am: 17. Feb 2018 19:08 Titel: |
 |
|
Die von Dir genannte Formel gilt für erzwungene Schwingungen, hier wird aber nichts erzwungen, unser System schwingt frei.
In der Formel steht nichts von Dämpfung. Falls Du das D meinst: das ist die Federkonstante. (Ja, ich weiß, in der Formelsammlung heißt sie k, aber in der Aufgabe D. Meine Meinung zu diesem Wirrwarr habe ich ja schon kundgetan.)
Einsetzen und ausrechnen.
|
|
 |
|

















