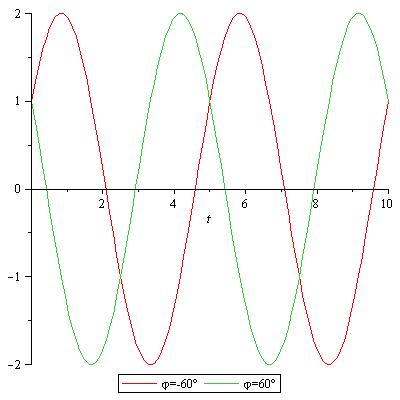
Schwingung - Nullphasenwinkel

L.i.t.t.l.e.13 · Anmeldungsdatum: 25.10.2007 Beiträge: 4

Hallo,

brauche leider Hilfe bei einer kleinen Physikaufgabe.
Die Aufg. lautet etwa wie folgt: Eine harmonische Schwingung hat die Frequenz 0,2 Hz, die Amplitude 2 cm und die Anfangsauslenkung 1 cm. Das Maximum der Schwingung kommt später.

Jetzt soll man unter anderem den Nullphasenwinkel berechnen. Der beträgt laut Lösung -60°.

Mir ist jetzt aber leider nicht klar, warum da ein minus davor steht.. ? Im Buch steht zwar ein Hinweis "(da Maximum später)", aber ich kann mir nichts darunter vorstellen. Und wie kann ich mir eine solche Schwingung überhaupt vorstellen, wenn die Anfangsauslenkung 1 cm, die Amplitude aber 2 cm beträgt.. ?

Hatte leider in der Oberstufe kein Physik mehr und jetzt im Studium hauts ganz schön rein ... :-(

Pls help ... Hilfe

Lg L.i.t.t.l.e.13

t.t. · Anmeldungsdatum: 04.10.2007 Beiträge: 113 Wohnort: Konstanz

Hallo L.i.t.t.l.e13,

erstmal willkommen im Forum

Nun zu deiner Frage:

Eine periodische Schwingung kann man ja mit der Formel

mathematisch ausdrücken. Ganz klar ist, dass man hier auf jeden Fall

setzen muss. Die Kreisfrequenz ist ja auch klar, die ist hier

.

Jetzt hast du als "Anfangsbedingung" deiner Schwingung gegeben, dass diese gerade 1cm sein soll. Das führt auf eine gleichung zur bestimmung des Nullphasenwinkels

.

Die Gleichung hat mehrere Lösungen. Normalerweise gibt man den Nullphasenwinkel in einem Bereich von -180° bis 180° an. Es bleiben also die Lösungen

und

.
Die Zusatzbedingung, dass das Maximum später durchlaufen werden soll (ist nicht toll ausgedrückt, besser wäre, dass das Maximum vor dem nächsten Nulldurchgang durchlaufen werden soll) lässt einen der Winkel ausschließen.

Als Verdeutlichung hilft da meistens die graphische Darstellung der Schwingung

Gruß T.T.

KUGA · Anmeldungsdatum: 30.07.2007 Beiträge: 21

bleibt da nicht auch noch die frage ob man mit sinus oder cosinus rechnet? das würde doch den winkel ändern. oder ist hier der cosinus konvetion?

t.t. · Anmeldungsdatum: 04.10.2007 Beiträge: 113 Wohnort: Konstanz

Stimmt der Winkel ist abhängig davon, welche Funktion man nutzt und das ist auch nicht Konvention. Aber das Ergebnis passt, deshalb würde ich hier den Cosinus nehmen.
Ein weiterer Grund für den Kosinus ist der, das Physiker gerne die komplexe Exponentialfunktion für Schwingungen nutzen und dann nur den Realteil als Amplitude betrachten und der ist grade der Kosinus.

Gruß T.T.

L.i.t.t.l.e.13 · Anmeldungsdatum: 25.10.2007 Beiträge: 4

Danke, die Grafik ist echt gut!

Mit der versteht man endlich was mit "das Maximum kommt später" gemeint ist. Thumbs up!

Hab bestimmt bald wieder eine Frage... :-)

L.i.t.t.l.e.13 · Anmeldungsdatum: 25.10.2007 Beiträge: 4

Hätte auch schon eine Frage. :-)

Und zwar, hieß die Aufgabe, dass man für ein Federpendel, dass einmalig ausgelenkt wird, nachweisen sollte, dass die Schwingung harmonisch ist.

Wie die Aufgabe gelöst wurde, ist mir klar. F = m * a und F = D * s gleichsetzen und auflösen, sodass am Ende w = Wurzel ( D / m ) rauskommt. Dazu habe ich aber zwei Verständnisfragen.

1.) Wieso ist damit bewiesen, dass die Schwingung harmonisch ist? Nehme an, weil die Gleichung, mit der die Auslenkung beschrieben wurde, ein cosinus/sinus enthält... Die Antwort befriedigt mich aber nicht, vlt auch wegen der nächsten:

2.) Wie kann ich mir die Gleichung m * a = D * s vorstellen? D * s ist doch am größten, wenn das Pendel maximal ausgelenkt ist. Ist an dem Punkt die Beschleunigung etwa auch maximal? Wie kommt es, dass beide Größen immer gleich sind?

Danke L.i.t.t.l.e.13

t.t. · Anmeldungsdatum: 04.10.2007 Beiträge: 113 Wohnort: Konstanz

Abend L.i.t.t.l.e.13,

ich glaube du hast da einen Vorzeichenfehler. Die Rücktreibende Kraft einer Feder ist entgegengesetzt zur Auslenkung.

Mit dem richtigen Vorzeichen erhällst du dann die Gleichung

Das ist die Differentialgleichung für eine harmonische Schwingung mit der Frequenz

. Differentialgleichung deshalb, weil in der Gleichung die Funktion

und die zweite Ableitung der Funktion

vorkommen.

Wenn du jetzt mal für

oder den Kosinus einsetzt wirst du sehen, dass die Gleichung gelöst wird.

Und ja die Gleichung heisst, dass die Beschleunigung am Punkt der maximalen Auslenkung von der Ruhelage auch Extremal wird, halt nur mit umgegehrtem Vorzeichen. Das liegt daran, dass die Feder die masse zurück in die Ruhelage bringen will.

Gruß T.T.