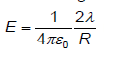| Autor |
Nachricht |
StromImpuls
Anmeldungsdatum: 14.07.2019
Beiträge: 51
|
 StromImpuls Verfasst am: 27. Dez 2019 23:29 Titel: Potential einer Linienladung StromImpuls Verfasst am: 27. Dez 2019 23:29 Titel: Potential einer Linienladung |
 |
|
Moin!
Weshalb steht im Zähler im ln das +d? Bekanntlich steht bei ln im Nenner der Abstand zur Linienladungsdichte und im Zähler der Abstand wo das Potential zu Null angenommen wird.
Wird denn das Potential folglich nicht nach Aufgabenstellung bei y=0 auf Null gesetzt? Wie kann dann der Zähler eine y-Komponente haben und dann noch +d.
| Beschreibung: |
|

Download |
| Dateiname: |
brucherat.png |
| Dateigröße: |
56.51 KB |
| Heruntergeladen: |
235 mal |
|
|
 |
StromImpuls
Anmeldungsdatum: 14.07.2019
Beiträge: 51
|
 StromImpuls Verfasst am: 30. Dez 2019 15:13 Titel: StromImpuls Verfasst am: 30. Dez 2019 15:13 Titel: |
 |
|
|
/push
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 30. Dez 2019 16:29 Titel: kingcools Verfasst am: 30. Dez 2019 16:29 Titel: |
 |
|
|
Leite es doch mal her
|
|
 |
StromImpuls
Anmeldungsdatum: 14.07.2019
Beiträge: 51
|
 StromImpuls Verfasst am: 30. Dez 2019 17:40 Titel: StromImpuls Verfasst am: 30. Dez 2019 17:40 Titel: |
 |
|
Also meinst du ich soll die Formel herleiten? Wir haben ja eine unendlich auszubreitende Linienladung. Das heißt wir müssen die Linienladungsdichte nicht durch n Punktladungen darstellen und können stattdessen wir folgt vorgehen:
2*pi*r*Länge*D=Q=Linienladungsdichte*Länge
<->
D=Linienladungsdichte/(2*pi*r)
E=D/e=Linienladungsdichte/(2*pi*r*e)
Jetzt die Richtungsinformation des Feldes beachten:
Vektor E=E*Basisvektor.
Wohin zeigt der Basisvektor bei einer Linienladungsdichte?
Ansonsten müsste ich noch eine Wegparametrisieren zwischen zwei Punkten oder wie bekomme ich das z und y aus der Musterlösung in meine Rechnung
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 30. Dez 2019 20:11 Titel: kingcools Verfasst am: 30. Dez 2019 20:11 Titel: |
 |
|
| Zitat: | | Ansonsten müsste ich noch eine Wegparametrisieren zwischen zwei Punkten oder wie bekomme ich das z und y aus der Musterlösung in meine Rechnung |
Was bedeutet denn r in deiner Formel? Ist das immer gleich egal wo ich bin?
|
|
 |
StromImpulse
Gast
|
 StromImpulse Verfasst am: 30. Dez 2019 20:22 Titel: StromImpulse Verfasst am: 30. Dez 2019 20:22 Titel: |
 |
|
Das r ist der Radius ( Kann man bei einer Linienladungsdichte von Radius sprechen?) Wo das Feld wirkt.
r kann man nun auch über den Betrag eines radius darstellen. Jetzt kommen wir aber zu meinen Ausgangsproblem. Hier scheitert es mit dem + bzw - d.
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 30. Dez 2019 20:35 Titel: kingcools Verfasst am: 30. Dez 2019 20:35 Titel: |
 |
|
|
Berechne doch mal r für verschiedene Positionen
|
|
 |
StromImpulse
Gast
|
 StromImpulse Verfasst am: 30. Dez 2019 20:40 Titel: StromImpulse Verfasst am: 30. Dez 2019 20:40 Titel: |
 |
|
|
(x,y,z)-(0,d,0) aber das Vorzeichen stimmt nicht im Zähler
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 30. Dez 2019 20:56 Titel: kingcools Verfasst am: 30. Dez 2019 20:56 Titel: |
 |
|
|
Eine x-Abhängigkeit liegt nicht vor, r beschreibt den senkrechten Abstand von der Linienladung. Laut http://wwwex.physik.uni-ulm.de/lehre/el-2008/node9.html ist das Potential mit nem Minuszeichen versehen. Das wurde offenbar in den Logarithmus gezogen (-log(x) = log(1/x)). Hilft das?
|
|
 |
StromImpulse
Gast
|
 StromImpulse Verfasst am: 30. Dez 2019 21:16 Titel: StromImpulse Verfasst am: 30. Dez 2019 21:16 Titel: |
 |
|
Hab es jetzt verstanden vielen dank. Aber um nun das Potential bei der Herleitung über
U= S E ds=phi=Phi b - Phi a ( Integration von a nach b)
Zu ermitteln wie sind die Grenzen zu bestimmen? Es ist ja nach dem Potential und nicht der Spannung gefragt.
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 30. Dez 2019 21:22 Titel: kingcools Verfasst am: 30. Dez 2019 21:22 Titel: |
 |
|
Versuch mal Latex zu verwenden 
Das Potential ist nur bis auf eine Konstante eindeutig bestimmt. Randbedingungen (z.B. Null im Unendlichen) liefern dann die Konstante. Hier hast du ja eine Randbedingung vorgegeben. Welche ist das?
|
|
 |
StromImpulse
Gast
|
 StromImpulse Verfasst am: 30. Dez 2019 21:51 Titel: StromImpulse Verfasst am: 30. Dez 2019 21:51 Titel: |
 |
|
Die Randbedingung ist phi(unendlich)=0
Dann komm ich aber auf phi(unendlich)-phi(a)=-phi(a)=-phi(r)....
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 30. Dez 2019 21:52 Titel: kingcools Verfasst am: 30. Dez 2019 21:52 Titel: |
 |
|
Du hast hier ja noch eine Platte gegeben 
|
|
 |
StromImpuls
Anmeldungsdatum: 14.07.2019
Beiträge: 51
|
 StromImpuls Verfasst am: 30. Dez 2019 22:11 Titel: StromImpuls Verfasst am: 30. Dez 2019 22:11 Titel: |
 |
|
Ich verstehe das irgendwie nicht. Die xz-Ebene ist ja die eine Platte die auf Nullpotential liegt. Dann haben wir noch unsere Linienladungsdichte die bei (0,d,0) liegt. Wenn ich das Potential angeben soll, dann ist das Potential zwischen der Platte und der Linienladungsdichte gefragt? Also nicht nur das Potential einer Linienladung ?
Handelt es sich dann nicht um eine Spannung ?
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 31. Dez 2019 02:55 Titel: kingcools Verfasst am: 31. Dez 2019 02:55 Titel: |
 |
|
|
Du hast noch eine Integrationskonstante die du bestimmen möchtest. Das kannst du über die Platte machen.
|
|
 |
StromImpulse
Gast
|
 StromImpulse Verfasst am: 31. Dez 2019 12:57 Titel: StromImpulse Verfasst am: 31. Dez 2019 12:57 Titel: |
 |
|
Hey, ich versuche gerade die genaue Herleitung bei der Potetialbestimmung einer Linienladungsdichte nachzuvollziehen. Dachte ja das ich es verstanden habe, aber das ist nicht so ganz der Fall. Ich kann in dem Link den du mir geschickt hast nicht ganz das U(r0) - die Integration von r0 bis r verstehen.
Was genau ist r0 und was ist r?
Bei einem Zylinderkondensator wäre die Integration ja einfach vom Inneren zum Äußeren Radius, also da wo sich das Feld befindet. Da die Linienladungsdichte unendlich dünn ist? kann sie doch kein inneren Radius haben und nur in einem Abstand r der nicht zu verwechseln ist mit dem Radius R.
Ich habe hier noch einige Denkprobleme wo ich unbedingt Hilfe brauche.
Lg & einen schönen rutsch Ihnen noch.
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 31. Dez 2019 13:14 Titel: kingcools Verfasst am: 31. Dez 2019 13:14 Titel: |
 |
|
|
Fang erstmal mit dem E-Feld der Linienladung an. Wenn du das richtig berechnen kannst dann sollte das Potential kein problem darstellen.
|
|
 |
StromImpulse
Gast
|
 StromImpulse Verfasst am: 31. Dez 2019 13:32 Titel: StromImpulse Verfasst am: 31. Dez 2019 13:32 Titel: |
 |
|
Es ist ja eine unendliche Linenladungsdichte. Im falle zb einer die sich auf der z Achse von -a bis +a befindet ginge man wie folgt vor:
Die Abhängigkeit der elektrischen Feldstärke E der Punktladung von Q umschreiben zu Q=Linienladungsdichte * dz
Jetzt dieseselektrische Feld integrieren von -a bis +a also folgt
S E dz von -a bis +a.
Wir haben aber eine unendlich lange Linienladungsdichte gegeben, wie sind da die Grenzen zu wählen?
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 31. Dez 2019 14:06 Titel: kingcools Verfasst am: 31. Dez 2019 14:06 Titel: |
 |
|
Na von -unendlich bis +unendlich.
| Zitat: | | Q=Linienladungsdichte * dz |
Es muss dQ lauten.
Wie lautet die Formel für das E-Feld einer Punktladung?
|
|
 |
Stromimpulse
Gast
|
 Stromimpulse Verfasst am: 31. Dez 2019 23:18 Titel: Stromimpulse Verfasst am: 31. Dez 2019 23:18 Titel: |
 |
|
In Betragsschreibweise:
E=1/(4*pi*e)*q/r^2
|
|
 |
StromImpulse
Gast
|
 StromImpulse Verfasst am: 01. Jan 2020 00:37 Titel: StromImpulse Verfasst am: 01. Jan 2020 00:37 Titel: |
 |
|
|
Ich habe jetzt alles verstanden außer wieso + und - d gilt.
|
|
 |
StromImpuls
Anmeldungsdatum: 14.07.2019
Beiträge: 51
|
 StromImpuls Verfasst am: 01. Jan 2020 01:56 Titel: StromImpuls Verfasst am: 01. Jan 2020 01:56 Titel: |
 |
|
Hey tut mir leid der LogIn hat irgendwie nicht funktioniert, da ich das Passwort nicht richtig geschrieben habe.
Kannst du mir bitte sagen wieso bei dem rotunterstrichenen es R und nicht R^2 sind und das noch wichtigere wieso es 2*lambda sind und nicht lambda*dR
| Beschreibung: |
|

Download |
| Dateiname: |
Unbenannt.png |
| Dateigröße: |
63.02 KB |
| Heruntergeladen: |
532 mal |
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 01. Jan 2020 13:06 Titel: kingcools Verfasst am: 01. Jan 2020 13:06 Titel: |
 |
|
|
Integriere das infinitesimale E-Feld (aka berechne das E-Feld einer unendlich ausgedehnten Linienladung) und du wirst es wissen.
|
|
 |
StromImpuls
Anmeldungsdatum: 14.07.2019
Beiträge: 51
|
 StromImpuls Verfasst am: 01. Jan 2020 13:38 Titel: StromImpuls Verfasst am: 01. Jan 2020 13:38 Titel: |
 |
|
Unendliche Linienladungsdichte:
Bei einer unendlichen Linienladungsdichte läuft es hinaus über DA=D*2*pi*r*l=Q=Lambda*l <-> E=D/e=lambda/(2*pi*r*l). Ich möchte aber verstehen wieso man auf dieses selbe Ergebnis kommt indem man man das im Anhang hochgeladene betrachtet.
Endliche Linienladungsdichte:
Mir ist bewusst das man bei einer endlichen Linienladungsdichte zb auf der z Achse von -a bis +a wie folgt vorgehen kann:
Elektrisches Feld einer Punktladung
E=1/(4*pi*e)*dQ/(r^2) mit dQ=Linienladungsdichte*dz und das nun integrieren von -a bis +a. So wird die endliche Linienladungsdichte durch n Punktladungen ausgedrückt/dargestellt.
Aber das im Anhang verwendet eine vollständg andere herangehensweise, da im Nenner nur eine Abhängigkeit von R anstatt R^2 ist und im Zähler eine 2 vorhanden ist. Am Ende kommt man auf das Ergebnis auf das elektrische Feld E eienr unendlich langen Linienladungsdichte.
Edit: Wenn ich wie du sagst das unendlich ausbreitende integriere dann komm ich ja auf eine Spannung bzw. Potential. Wieso soll ich da sehen weshalb man eine 2 im Zähler in einem Rechenschritt davor hat...
| Beschreibung: |
|
| Dateigröße: |
1.23 KB |
| Angeschaut: |
2297 mal |
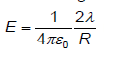
|
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 01. Jan 2020 13:43 Titel: kingcools Verfasst am: 01. Jan 2020 13:43 Titel: |
 |
|
|
Du kommst nicht auf ein Potential, da du erst dE betrachtest und durchs Integrieren E erhälst und nicht Phi.
|
|
 |
StromImpulse
Gast
|
 StromImpulse Verfasst am: 03. Jan 2020 01:27 Titel: StromImpulse Verfasst am: 03. Jan 2020 01:27 Titel: |
 |
|
Ich verstehe nicht wie man das r und r0 hier zu wählen hat damit man auf die Musterlösung kommt. Ich habe heute alle verschiedenen Potentiale hergeleitet
(endliche und unendliche Ladungsverteilungen)
phi=lambda/(2*pi*e) ln(r/r0). Ich kann die komplette Herleitung nachvollziehen
Auch das lnr-ln ro = ln(r/r0) hilft mir nicht weiter. ro ist doch in Zylinderkoordinaten ausgedrückt der Punkt an dem das Nullpotential angenommen wird und r der Ort das Bezugspunktes
|
|
 |
StromImpulse
Gast
|
 StromImpulse Verfasst am: 04. Jan 2020 00:21 Titel: StromImpulse Verfasst am: 04. Jan 2020 00:21 Titel: |
 |
|
|
Ich habe es jetzt endlich verstanden! Ich denke es ist wichtig zu erwähnen, dass es sich die ganze Zeit um eine Spegelladungaufgabe handelt, d.h. man kommt auf die Lösung in dem man die Potentiale der Originalladung und der Spiegelladung addiert.
|
|
 |
kingcools
Anmeldungsdatum: 16.01.2011
Beiträge: 700
|
 kingcools Verfasst am: 05. Jan 2020 15:44 Titel: kingcools Verfasst am: 05. Jan 2020 15:44 Titel: |
 |
|
|
Sehr schön!
|
|
 |
|