| Autor |
Nachricht |
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
 mister Verfasst am: 23. Aug 2016 17:22 Titel: Elektrisches Potential |
 |
|
Hey,
ich versuche gerade das elektr. Potential zu verstehen, jedoch habe ich damit ein paar Probleme.
Es ist definiert als: =-\int_{P}^{P_0}E\cdot ds) und ist im Prinzip die potentiell Energie, die gebraucht wird, wenn man eine Einheitsladung im Feld E vom Bezugspunkt P0 zu einem Punkt P transportiert.
Weil es eine einheitsladung ist, kann man ja einfach statt der Kraft F, das Feld E nehmen, da ja gilt F=E*q.
Nun kommt der unverständliche Teil - Zitat:
"Für eine einzelne Ladung im Ursprung ist das Potential in jedem Punkt folgendes:  = \frac{q}{4\pi\epsilon_0}\frac{1}{r})
Ich nehme an, dass das Feld E von der Punktladung q erzeugt wird und es sich radial ausbreitet. Und mein Bezugspunkt P0 ist der Ursprung. Nun wollen wir eine Einheitsladung von P0 zum Punkt P transportieren. Wenn wir das Potential wissen wollen, dann müssen wir nur für r den Betrag vom Punkt P einsetzen. (Also Abstand zwischen P0 und P) und fertig.
Ist genau das mit diesem obigen Zitat gemeint?
Gruß
Mister
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 23. Aug 2016 21:15 Titel: |
|
|
| mister hat Folgendes geschrieben: | | Und mein Bezugspunkt P0 ist der Ursprung. |
Aber nur, wenn der Ursprung im Unendlichen liegt. Du weißt, dass das Potential das Wegintegral der Feldstärke ist (hast Du ja selber geschrieben). Stell' also mal die Feldstärkeformel für ein kugelsymmetrisches Feld auf und integriere von r bis r0. Dann siehst Du, was ich meine.
|
|
|
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
| mister Verfasst am: 24. Aug 2016 12:29 Titel: |
|
|
Ja, jetzt wird es mir klar! Danke.
=\frac{q}{4\pi\epsilon_0}\frac{1}{r^2}) und wenn ich das dann wie oben integriere kommt genau die Potentialformel raus, wo man gut sehen kann, dass dies mit 1/r abnimmt.
Dann habe ich noch eine Frage zum Überlagerungsprinzip bitte:
Dieses gilt sowohl beim elektr. Feld, als auch beim elektr. Potential.
1. Es ist klar, dass ich ein überlargertes Feld habe, wenn wenn ich 2 oder mehrere Punktladungen nebeneinander setze.
D.h., wenn ich ein Objekt, z.B. einen Draht oder was auch immer, elektr. auflade, dann habe ich schon ein überlagertes Feld?
2. Angenommen wir haben irgendein Objekt mit einer Ladungsdichte  . Wenn ich mir nun das elektr. Potential an einem Punkt ausrechnen möchte, dann brauch ich ja zuerst eine Formel für das elektr. Feld E, um dann das zu integrieren können, nehme ich an.
Hier muss man dann die einzelnen Felder aufintegrieren, also wenn ich meine obige E-Feld Formel umändere in:
=\frac{\lambda}{4\pi\epsilon_0}\int \frac{1}{r^2}dV) - Kann ich das dann so schreiben?
3. Wie habe ändere ich obige Formel um, wenn ich z.B. einen Draht oder Kugel habe?
Es ist klar, dass bei einer Kugel, dasselbe rauskommt, wie bei einer Punktladung, aber ich möchte einfach sehen, wie alles zusammenhängt.
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 24. Aug 2016 14:18 Titel: |
|
|
| mister hat Folgendes geschrieben: | 1. Es ist klar, dass ich ein überlargertes Feld habe, wenn wenn ich 2 oder mehrere Punktladungen nebeneinander setze.
D.h., wenn ich ein Objekt, z.B. einen Draht oder was auch immer, elektr. auflade, dann habe ich schon ein überlagertes Feld?
|
Im Prinzip ja. Allerdings rechnet man das Feld einer Linienladung anders aus, indem man sich nämlich die Zylindergeometrie des Feldes zunutze macht und den Gaußschen Flusssatz anwendet.
| mister hat Folgendes geschrieben: | | - Kann ich das dann so schreiben? |
Nein. Abgesehen davon, dass nicht klar ist, welches infinitesimal kleine Volumen mit dV gemeint ist, fehlt auch die physikalische Begründung für eine solche Vorgehensweise. Insbesondere wird dabei nicht berücksichtigt, dass die Feldstärken infolge jeder einzelnen auf der Geraden liegenden Punktladung in dem betrachteten Punkt unterschiedliche Richtungen haben.
| mister hat Folgendes geschrieben: | Wie habe ändere ich obige Formel um, wenn ich z.B. einen Draht oder Kugel habe?
Es ist klar, dass bei einer Kugel, dasselbe rauskommt, wie bei einer Punktladung, aber ich möchte einfach sehen, wie alles zusammenhängt. |
Der prinzipielle Zusammenhang ergibt sich, wie gesagt, aus dem Gaußschen Flusssatz. Den solltest Du Dir mal im Lehrbuch oder bei wiki oder ... oder ... anschauen.
|
|
|
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 24. Aug 2016 15:51 Titel: |
|
|
| mister hat Folgendes geschrieben: | | Von was für einer Geometrie geht das Wiki hier aus? |
Von beliebiger Geometrie.
| Mister hat Folgendes geschrieben: | | Da es sich um eine Raumladungsdichte handelt bestimmt nicht von einem dünnen Draht. |
Aber Du bist von einem (dünnen) Draht ausgegangen. Jedenfalls hast Du eine Linienladungsdichte vorgegeben. Und hast damit ein Integral angegeben, welches sich deutlich von dem bei wiki unterscheidet und ja noch nicht einmal dimensionsmäßig stimmt. Die Dimension der Feldstärke ist Spannung pro Länge, die Feldstärke nach Deiner Gleichung hat aber die Dimension Spannung mal Länge. Also, irgendwie verstehe ich Deine Argumentation nicht.
Warum folgst Du nicht mal meinem Rat und schaust Dir den Gaußschen Flusssatz an?
|
|
|
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
| mister Verfasst am: 24. Aug 2016 18:51 Titel: |
|
|
Danke, hab mir dieses Gesetz nun in Feynman's Vorlesungen durchgelesen.
Es besagt ja, dass
ist, also das gschlossene Oberflächenintegral eines E-Feldes ist gleich dem Volumenintegral der Divergenz des E-Feldes.
S ist eine geschlossene Fläche, V das eingschlossenen Volumen und n der Normaleinheitsvektor, der normal auf die infinitesimale Fläche 'da' steht.
Dann ist noch ganz wichtig zu sagen, dass laut der Maxwell-Gleichung  ist.
Gut, dann wenden wir das mal auf das Draht-Beispiel an:
Die beste gedachte Fläche ist hier ein Zylinder und innerhalb sollten sich die Ladungen, also der Draht, befinden.
Dann muss  gelten.
Also dieses Gesetz vereinfacht wirklich alles sehr.
Aber es gilt nur, wenn sich das E-Feld radial/kugelsymmetrisch ausbreitet, richtig? Beim Draht geht das auch nur, weil wir ihn unendlich lang darstellen.
D.h. solange sich im Inneren einer noch so unsymmetrischen geschlossenen Fläche eine Punktladung befinden, kann man das Gauß'sche Gesetz anwenden?
Dann wird das E-Feld zwar nicht exakt radial auf die Oberfläche auftreten, aber das Gesetz gilt.
|
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 24. Aug 2016 19:10 Titel: |
|
|
| mister hat Folgendes geschrieben: |
Aber es gilt nur, wenn sich das E-Feld radial/kugelsymmetrisch ausbreitet, richtig? Beim Draht geht das auch nur, weil wir ihn unendlich lang darstellen.
D.h. solange sich im Inneren einer noch so unsymmetrischen geschlossenen Fläche eine Punktladung befinden, kann man das Gauß'sche Gesetz anwenden?
Dann wird das E-Feld zwar nicht exakt radial auf die Oberfläche auftreten, aber das Gesetz gilt. |
Das gaußsche Gesetz gilt natürlich immer. Aber es praktisch anwenden um das elektrische Feld zu berechnen, geht eigentlich nur in sehr symmetrischen Situationen, in denen man was zur Richtung des E-Feldes sagen kann.
|
|
|
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
| mister Verfasst am: 26. Aug 2016 12:43 Titel: |
|
|
Ok, vestehe.
Jedoch ist mir noch nicht ganz klar, wie man genau auf  kommt.
Feynman hat das folgendermaßen beschrieben:
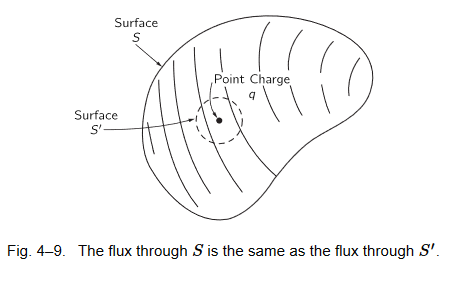
| Zitat: | | Angenommen wir "entfernen" die Ladung aus dem "Innern", indem wir sie mit einer Fläche S' umgeben, die vollständig innerhalb der ursprünglichen Fläche S liegt(siehe Anhang). Das Volumen, das zwischen den beiden Flächen S und S' eingeschlossen ist, enthält nun keine Ladung. Der Gesamtfluss aus diesem Volumen (einschließlich dem durch S') ist Null. Der Fluss durch S ist derselbe wie der Fluss durch S'. |
Jetzt meine Frage:
Es ist klar, dass der Fluss aus dem Volumen zwischen S' und S Null ist, unabhängig davon wie jetzt S' und S genau aussieht.
Der Fluss durch S' und S muss auch derselbe sein, da ja sonst auch der Fluss aus dem Volumen zwischen S' und S nicht Null sein kann, da dieser sich ja aufhebt.
Die Form von der fläche ist deswegen egal, da es ja unendlich viele kleine Feldlinien gibt, die durch diese Fläche gehen. Angenommen die Ladung ist außerhalb eine komischen unsymmetrischen Fläche. Die Feldlinien gehen links in die Fläche rein und rechts raus. Der Fluss links ist gleich dem Fluss rechts, weil es wie gesagt unendlich viele Feldlinien gibt und da die Form der Fläche immer egal sein wird. - Stimmt das so?
Und wenn ich jetzt S' als Kugeloberfläche wähle, dann bekomme ich als Fluss raus und da der Wert unabhängig von dessen Flächen erscheint, gilt das überall.
Hmm, ist das so richtig gesagt? Während dem Versuch des Erklärens wurde es mir deutlich klarer^^.
| Beschreibung: |
|
| Dateigröße: |
12.12 KB |
| Angeschaut: |
5942 mal |
|
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 26. Aug 2016 13:06 Titel: |
|
|
Ja. Der von q ausgehende Fluss muss durch jede beliebige Hüllfläche hindurch, er kann ja nicht irgendwo versickern, sofern sich nicht weitere Ladungen im von der Hüllfläche eingeschlossenen Volumen befinden. Zur Berechnung eignet sich dann besonders eine konzentrische Kugelfläche um die Ladung herum. Denn aus Symmetriegründen
1. ist der Betrag der Flussdichte an jeder Stelle der Kugeloberfläche derselbe und
2. sind Flussdichtevektor und Flächenvektor an jeder Stelle der Kugeloberfläche parallel,
was die Berechnung des Integrals wesentlich vereinfacht.
|
|
|
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
| mister Verfasst am: 26. Aug 2016 17:51 Titel: |
|
|
Ein Beispiel ist noch interessant, wo das Gauß'sche Gesetz eine Rolle spielt:
Angenommen wir haben 3 negative Ladung an den Ecken einens gleichseitigen Dreiecks und in der Mitte platzieren wir eine pos. Ladung.
Ich würde sagen, dass sich alle 4 Ladungen nicht bewegen dürfen, da die pos. Ladung die anderen im Gleichgewicht hält.
Jedoch ist die auf die pos. Ladung wirkende Kraft Null.
1. Wenn man sagt "Die Kraft wird auf diese Ladung", dann meint man die Kraft, die von der Ladung wegwirkt oder? Also ein Pfeil nach außen irgendwo?
2. Warum ist dann die Kraft auf die pos. Ladung Null?
Ich weiß, dass wenn sich eine neg. und pos. Ladung nebeneinander befinden, dass sie sich dann anziehen. Bei zwei neg. Ladungen würden die sich abstoßen, bis sich die Kräfte nicht mehr gegenseitig beeinflussen würden.
Und wenn ein Gleichgewicht besteht, dann muss die Gegenkraft gleich der Kraft die auf die Ladung wirkt sein.
(später wird dann mit dem Gauß'schen Gesetz bewiesen, dass es keine stabile Gleichgewichtslage gibt)
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 27. Aug 2016 14:16 Titel: |
|
|
| mister hat Folgendes geschrieben: | | Ich würde sagen, dass sich alle 4 Ladungen nicht bewegen dürfen, da die pos. Ladung die anderen im Gleichgewicht hält. |
Es ist gerade umgekehrt. Die drei Eckladungen halten die positive ladung im Gleichgewicht. Dafür müssen die drei Eckenladungen ortsfest gehalten werden, sonst würden sie sich auf die positive Ladung zubewegen.
| mister hat Folgendes geschrieben: | | 1. Wenn man sagt "Die Kraft wird auf diese Ladung", dann meint man die Kraft, die von der Ladung wegwirkt oder? Also ein Pfeil nach außen irgendwo? |
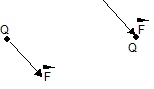
Nee, dieselbe Kraft kann man auch als zur Ladung hin gerichtet sehen. Siehe Skizze unten.
| mister hat Folgendes geschrieben: | | 2. Warum ist dann die Kraft auf die pos. Ladung Null? |
Weil die Vektorsumme der drei gleich großen um 120° gegeneinander verdrehten Kräfte Null ist. Sie bilden nämlich ebenfalls ein gleichseitiges Dreieck.
| Beschreibung: |
|
| Dateigröße: |
2.97 KB |
| Angeschaut: |
5903 mal |
|
| Beschreibung: |
|
| Dateigröße: |
3.84 KB |
| Angeschaut: |
5903 mal |
|
|
|
|
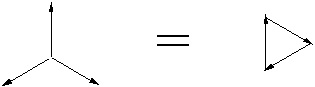
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
| mister Verfasst am: 27. Aug 2016 19:21 Titel: |
|
|
| GvC hat Folgendes geschrieben: |
Es ist gerade umgekehrt. Die drei Eckladungen halten die positive ladung im Gleichgewicht. Dafür müssen die drei Eckenladungen ortsfest gehalten werden, sonst würden sie sich auf die positive Ladung zubewegen. |
Achso ja, jetzt ist es klar. Was ist wenn die Ladungen in einer Reihe folgendermaßen angeordnet sind? neg., pos., neg. - Wenn hier die neg. Ladungen wieder ortsfest sind, dann halten die neg. Ladungen die pos. im Gleichgewicht oder?
| Zitat: |
Nee, dieselbe Kraft kann man auch als zur Ladung hin gerichtet sehen. Siehe Skizze unten. |
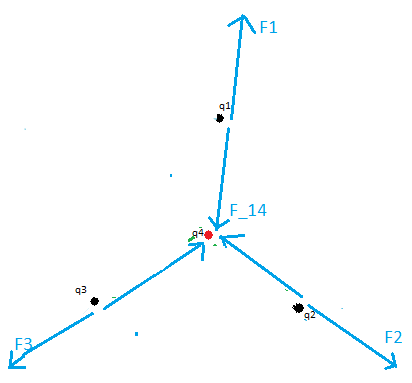
Welche Kraft meint man dann, wenn man folgendes sagt: "die auf die pos. Ladung wirkende Kraft". F1 oder F2 im Bild?
F1 zeigt ja zur pos. Ladung und F2 halt weg.
| Zitat: |
Weil die Vektorsumme der drei gleich großen um 120° gegeneinander verdrehten Kräfte Null ist. Sie bilden nämlich ebenfalls ein gleichseitiges Dreieck. |
Aber diese drei Kräfte haben denselben Betrag, wie kann dann eine Summe aus den dreien Null ergeben? Die Beziehung mit dem gleischseitigen Dreieck ist mir noch nciht so klar hier.
| Beschreibung: |
|
| Dateigröße: |
612 Bytes |
| Angeschaut: |
5891 mal |
|
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 28. Aug 2016 12:22 Titel: |
|
|
| mister hat Folgendes geschrieben: | | Was ist wenn die Ladungen in einer Reihe folgendermaßen angeordnet sind? neg., pos., neg. - Wenn hier die neg. Ladungen wieder ortsfest sind, dann halten die neg. Ladungen die pos. im Gleichgewicht oder? |
Nicht notwendigerweise. Das ist nur an einer ganz bestimmten Position der positiven Ladung der Fall, nämlich an der Stelle, an der die Kräfte infolge der beiden negativen Ldungen betragsmäßig gleich groß sind und sich somit aufheben.
| mister hat Folgendes geschrieben: | | Welche Kraft meint man dann, wenn man folgendes sagt: "die auf die pos. Ladung wirkende Kraft". F1 oder F2 im Bild? |
Du hast es doch selber eingezeichnet: Auf die positive Ladung wirkt die Kraft F2, auf die negative Ladung die Kraft F1. Beide Kräfte sind betragsmäßig gleich groß, wie das in statischen physikalischen Systemen immer so ist: actio = reactio.
| mister hat Folgendes geschrieben: | | Aber diese drei Kräfte haben denselben Betrag, ... |
... aber unterschiedliche Richtung.
| mister hat Folgendes geschrieben: | | ... wie kann dann eine Summe aus den dreien Null ergeben? Die Beziehung mit dem gleischseitigen Dreieck ist mir noch nciht so klar hier. |
Kräfte sind Vektoren. Deren Summe ergibt sich, wenn sie geometrisch addiert werden, wenn also der Fußpunkt eines Kraftpfeils unter Beibehaltung seiner Richtung an die Spitze des anderen Kraftpfeils gelegt wird. Im vorliegenden Fall ergibt sich das gleichseitige Dreieck durch Parallelverschiebung von zweien der drei Kräfte.
|
|
|
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
| mister Verfasst am: 29. Aug 2016 11:32 Titel: |
|
|
Jap, jetzt ist es klar, danke.
Wenn man statt unserer ursprünglichen Ladungsanordnung, die neg. Ladungen so verteilt, dass sie ein Sechseck ergeben und in der Mitte die pos. Ladungen sind, dann kann ich meine Kräfte ja so verschieben, dass diese zwei gleichseitige Dreiecke bilden und da die Summe der Kräfte von beiden Dreiecken jeweils Null ist, ist auch die Gesamtkraft Null.
1.
-----------
Logischerweise wirkt doch auch eine Kraft von den jeweils neg. Ladungen zur pos. Ladung. (also die Kraft auf die neg. Ladung - also nennt man ja so, wenn der Pfeilf von neg. zu pos. zeigt)
D.h. ich könnte auch diese Kraftvektoren verschieben und sehen, dass auch dessen Summe Null ist, da die Pfeile ja nur in die andere Richtung zeigen. Wichtig ist nur, dass die neg. Ladungen ortsfest sind. - richtig?
-----------
2.
-----------
Was würde z.B. passieren, wenn beim Sechseck die neg. Ladungen nicht ortsfest sind, dann würden sich ja die neg. Ladungen abstoßen, da der Abstand so groß ist, wie zur pos. Ladung, also die Kraft ausreicht zwischen den neg. Ladungen ausreicht, um diese wegzustoßen.
Aber kann es sein, dass alles trotzdem im Gleichgewicht ist, da einerseits sich die neg. Ladungen versuchen zu wegstoßen, aber andererseits die pos. Ladung alle neg. Ladungen anzieht.
Die pos. Ladung bewegt sich ja nicht, da von allen Seiten die Kräfte der neg. Ladungen wirken.
------------
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 29. Aug 2016 14:56 Titel: |
|
|
| mister hat Folgendes geschrieben: | | Wenn man statt unserer ursprünglichen Ladungsanordnung, die neg. Ladungen so verteilt, dass sie ein Sechseck ergeben und in der Mitte die pos. Ladungen sind, dann kann ich meine Kräfte ja so verschieben, dass diese zwei gleichseitige Dreiecke bilden und da die Summe der Kräfte von beiden Dreiecken jeweils Null ist, ist auch die Gesamtkraft Null. |
Man kann die 6 gleich großen Kräfte auch zu einem geschlossenen Sechseck zusammenfügen und so erkennen, dass die Gesamtkraft auf die mittlere Ladung Null ist.
Zu 1. Kraft auf die negativen Eckenladungen
| mister hat Folgendes geschrieben: | | D.h. ich könnte auch diese Kraftvektoren verschieben und sehen, dass auch dessen Summe Null ist, da die Pfeile ja nur in die andere Richtung zeigen. |
Du wirst sehen, dass die Gesamtkraft auf jede negative Eckenladung nur dann Null ist, wenn die positive Ladung in der Mitte betragsmäßig genauso groß ist wie jede der negativen Ladungen an den Ecken des Dreiecks. Ist die positive Ladung größer als die Eckladungen, überwiegt die Anziehungskraft zwischen positiver Ladung und den negativen Eckladungen. Ist sie kleiner, überwiegen die Abstoßungskräfte der jeweils beiden anderen Eckladungen.
| mister hat Folgendes geschrieben: | | Was würde z.B. passieren, wenn beim Sechseck die neg. Ladungen nicht ortsfest sind, dann würden sich ja die neg. Ladungen abstoßen, da der Abstand so groß ist, wie zur pos. Ladung, also die Kraft ausreicht zwischen den neg. Ladungen ausreicht, um diese wegzustoßen. |
Nein, das kann man so nicht sagen. Ob die Abstoßungskräfte zwischen den negativen Ladungen die Anziehungskraft durch die positive Ladung überwiegen, hängt wie bei der dreiecksförmigen Anordnung einzig und allein von der Größe der positiven Ladung ab.
|
|
|
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
| mister Verfasst am: 29. Aug 2016 15:48 Titel: |
|
|
| GvC hat Folgendes geschrieben: |
Du wirst sehen, dass die Gesamtkraft auf jede negative Eckenladung nur dann Null ist, wenn die positive Ladung in der Mitte betragsmäßig genauso groß ist wie jede der negativen Ladungen an den Ecken des Dreiecks. Ist die positive Ladung größer als die Eckladungen, überwiegt die Anziehungskraft zwischen positiver Ladung und den negativen Eckladungen. Ist sie kleiner, überwiegen die Abstoßungskräfte der jeweils beiden anderen Eckladungen.
|
Hm verstehe hier nicht, was du genau meinst. Warum spielen die Abstoßungskräfte(zwischen den Eckladungen) hier überhaupt eine Rolle, da diese eh ortsfest sind?
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 29. Aug 2016 16:05 Titel: |
|
|
| mister hat Folgendes geschrieben: | | Warum spielen die Abstoßungskräfte(zwischen den Eckladungen) hier überhaupt eine Rolle, da diese eh ortsfest sind? |
Du hattest ja davon angefangen. Oder hattest Du unter Deinem Punkt 1 etwas anderes gemeint? Ich hatte jedenfalls den Eindruck, dass Du meintest, die elektrischen Abstoßungs- und Anziehungskräfte addierten sich zu Null. Das ist nur für den Sonderfall richtig, dass positive Mitten- und negative Eckladung betragsmäßig gleich groß sind. Wenn die negativen Ladungen ortsfest sind, ist zwar mit Ausnahme des einen Sonderfalls die Summe der elektrischen Kräfte nicht Null, die Gesamtkraft jedoch ist Null. Denn es addiert sich noch eine mechanische Haltekraft dazu, die die Ladungen an ihrer Position hält.
|
|
|
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
| mister Verfasst am: 29. Aug 2016 18:09 Titel: |
|
|
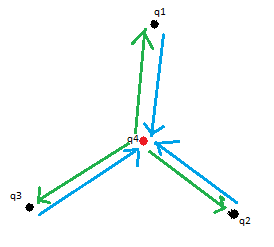
Ich hab nochmals ein Bild dazu gemalt.
Die eingezeichnenten Kräfte wirken ja immer genau so, wenn sich Ladungen nebeneinander befinden.
Die Gesamtkraft auf q4 bilden die grünen Kraftpfeile. Diese Kraft ist eben Null, was eh schon geklärt ist.
Die blauen Kraftpfeile sind die jeweiligen Kräfte die auf je eine neg. Ladung q1-3 wirken.
Wenn ich so darüber nachdenke, ergibt es doch keinen Sinn diese blauen Kraftvektoren überhaupt zu addieren. Für das Gleichgewicht, ist sowieso nur der Gesamtvektor auf q4(pos. Ladung) wichtig, denn der muss Null werden.
Die einzelnen Fälle:
- neg. und pos. Ladung betragsmäßig gleich und neg. Ladungen ortsfest: d.h. hier sind grüne und blaube Kraftpfeile betragsmäßig gleich und heben sich vektoriell auf? In diesem Fall wäre die pos. Ladung dann auch im Gleichgewicht, falls die neg. Ladungen nicht ortsfest wären, oder würden da die Abstoßungskräfte zwischen den neg. Ladungen (q1 u. q2 etc.) stören?
- neg. und pos. Ladung nicht betragsmäßig gleich und neg. Ladungen ortsfest:
Angenommen die pos. Ladung ist größer als die einzelnen neg. Ladungen, dann ist ein grüner Kraftvektor größer als der blaue Kraftvektor. Wenn die neg. Ladungen nicht ortsfest sind, dann besteht trotzdem gleichgewicht oder?
Angenommen die pos. Ladung ist kleiner als die einzelnen neg. Ladungen, dann ist jetzt der blaue Kraftvektor größer als der grüne und die neg. Ladungen werden von der positiven angezogen, falls die neg. Ladungen nicht ortsfest sind.
Sind aber die negativen Ladungen ortsfest, jedoch pos. und neg. Ladung betragsmäßig verschieden, besteht jedoch immer ein Gleichgewicht, da die Gesamtkraft auf die pos. Ladung immer verschwindet.
So stimmts jetzt?
| Beschreibung: |
|
| Dateigröße: |
3.14 KB |
| Angeschaut: |
5828 mal |
|
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 30. Aug 2016 01:18 Titel: |
|
|
| mister hat Folgendes geschrieben: | | Wenn ich so darüber nachdenke, ergibt es doch keinen Sinn diese blauen Kraftvektoren überhaupt zu addieren. |
So ist es. Denn die drei "blauen" Kräfte wirken jede auf eine andere Ladung und stellen lediglich die Anziehungskraft zwischen der jeweiligen Eckladung und der Mittenladung dar. Auf die Eckladungen wirken noch weitere Kräfte, nämlich die Abstoßungskräfte infolge der beiden jeweils benachbarten Eckladungen. In der hier ursprünglich gestellten Frage ging es aber ausschließlich um die Ladung in der Mitte. Und dort sind auch alle Kräfte eingetragen (grün).
| mister hat Folgendes geschrieben: | | Für das Gleichgewicht, ist sowieso nur der Gesamtvektor auf q4(pos. Ladung) wichtig, denn der muss Null werden. |
Ja, für das Gleichgewicht der mittleren Ladung q4. Wenn Du feststellen willst, ob sich das aus 4 Ladungen bestehende Gesamtsystem im Gleichgewicht befindet, musst Du alle Kräfte berücksichtigen, die Du aber gar nicht alle eingezeichnet hast.
| mister hat Folgendes geschrieben: | | - neg. und pos. Ladung betragsmäßig gleich und neg. Ladungen ortsfest: d.h. hier sind grüne und blaube Kraftpfeile betragsmäßig gleich und heben sich vektoriell auf? |
Nein, so kann man das nicht sagen. Grüne und blaue Kraftpfeile würden sich nur dann gegenseitig aufheben, wenn Du alle Kräfte berücksichtigen würdest, was aus Deiner Skizze aber nicht hervorgeht. Da fehlen insgesamt 6 (blaue) Kraftpfeile (zwei zusätzliche auf jede der drei Eckladungen).
| mister hat Folgendes geschrieben: | | In diesem Fall wäre die pos. Ladung dann auch im Gleichgewicht, falls die neg. Ladungen nicht ortsfest wären, oder würden da die Abstoßungskräfte zwischen den neg. Ladungen (q1 u. q2 etc.) stören? |
Wenn alle Ladungen gleichen Betrag haben, dann ist das Gesamtsystem im Gleichgewicht und demzufolge wären auch alle Ladungen ortsfest. Die Abstoßungskräfte zwischen den negativen Ladungen würden nicht "stören", sondern im Gegenteil: sie sorgen dafür, dass das System sich im Gleichgewicht befindet. (Allerdings handelt es sich um ein sehr labiles Gleichgewicht.)
| mister hat Folgendes geschrieben: | | Angenommen die pos. Ladung ist größer als die einzelnen neg. Ladungen, dann ist ein grüner Kraftvektor größer als der blaue Kraftvektor. Wenn die neg. Ladungen nicht ortsfest sind, dann besteht trotzdem gleichgewicht oder? |
Deine Überlegungen kranken daran, dass Du jeweils nur eine der drei Kräfte (blau) auf die negativen Ladungen betrachtest. Das gesamte System besteht aus vier Ladungen. Auf jede der vier Ladungen wirken also drei Kräfte infolge der elektrischen Felder der drei anderen Ladungen. Du hast doch auch drei Kräfte auf die Mittenladung identifiziert (die sich gegenseitig aufheben), warum tust Du das nicht auch für die drei Eckladungen? Bei den Eckladungen betrachtest du aber offenbar nur einen Kraftpfeil, nämlich den, der auf die Mittenladung hin gerichtet ist. Der ist immer genauso groß, wie derjenige der drei grünen Pfeile, der zu der jeweilgen Eckladung hin gerichtet ist. Und was ist mit den beiden anderen (abstoßenden) Kräfte, die ja auch auf jede Eckladung wirken?
Wenn die positive Ladung größer als jede negative Ladung ist, befindet sich das System nicht im statischen Gleichgewicht, es sei denn die negativen Eckladungen würden an ihren Positionen durch irgendeine Vorrichtung festgehalten werden. Anderenfalls würden sie sich auf die positive Ladung zubewegen, da die Anziehungskraft zwischen der mittleren Ladung und jeder Eckladung größer ist als die Summe der beiden abstoßenden Kräfte auf jede Eckladung.
| mister hat Folgendes geschrieben: | | Angenommen die pos. Ladung ist kleiner als die einzelnen neg. Ladungen, dann ist jetzt der blaue Kraftvektor größer als der grüne und die neg. Ladungen werden von der positiven angezogen, falls die neg. Ladungen nicht ortsfest sind. |
Nein, nein. Irgendwie hast Du eine sehr abenteuerliche Vorstellung von den elektrostatischen Kräften. Um in Deinem Bild zu bleiben: Jede der drei grünen Kräfte wäre kleiner als die Summe aller drei blauen Kräfte auf eine Eckladung. Die positive Ladung wäre zwar im Gleichgewicht (sofern die drei Eckladungen gleich groß sind), die negativen Ladungen würden sich aber von der Mittenladung wegbewegen, d.h. das System befände sich nicht in einem statischen Gleichgewicht.
Ich empfehle Dir, mal die Gesamtkraft auf jede Eckladung zu bestimmen, oder vielleicht auch zunächst mal nur die abstoßende Kraft auf jede Eckladung, und die mit der Anziehungskraft infolge des Feldes der mittleren Ladung zu vergleichen. Dann wird sich möglicherweise der Knoten in Deinem Gehirn entwirren.
|
|
|
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
| mister Verfasst am: 30. Aug 2016 11:51 Titel: |
|
|
Danke, es ist klarer geworden.
| Zitat: | Ja, für das Gleichgewicht der mittleren Ladung q4. Wenn Du feststellen willst, ob sich das aus 4 Ladungen bestehende Gesamtsystem im Gleichgewicht befindet, musst Du alle Kräfte berücksichtigen, die Du aber gar nicht alle eingezeichnet hast.
Nein, so kann man das nicht sagen. Grüne und blaue Kraftpfeile würden sich nur dann gegenseitig aufheben, wenn Du alle Kräfte berücksichtigen würdest, was aus Deiner Skizze aber nicht hervorgeht. Da fehlen insgesamt 6 (blaue) Kraftpfeile (zwei zusätzliche auf jede der drei Eckladungen). |
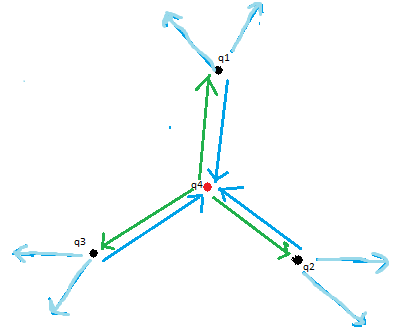
Okay, jetzt habe ich die fehlenden Kraftvektoren, die auf die Eckladungen wirken, ergänzt(hellblau).
| Zitat: | | Wenn alle Ladungen gleichen Betrag haben, dann ist das Gesamtsystem im Gleichgewicht und demzufolge wären auch alle Ladungen ortsfest. Die Abstoßungskräfte zwischen den negativen Ladungen würden nicht "stören", sondern im Gegenteil: sie sorgen dafür, dass das System sich im Gleichgewicht befindet. (Allerdings handelt es sich um ein sehr labiles Gleichgewicht.) |
Also, wenn alle Ladungen den gleichen Betrag haben, dann ist doch die Gesamtkraft der jeweiligen hellblauen Pfeile betragsmäßig genau so groß, wie der jeweilige blaue Pfeil. Und da diese entgegengesetzt(Blau und Hellblau_gesamt) sind, hebt sich die Kraft auf. Und jetzt ist es klar, dass man eben nicht sagen darf, dass sich grüne und blaue Pfeile aufheben dürfen, da man die Hellblauen nicht vergessen darf. Grünen Pfeile heben sich eh schon wie ganz oben beschrieben auf und das System befindet sich im labilen Gleichgewicht. - Labil wahrscheinlich, weil die Ladungen halt nicht 100% festgemacht sind, also kann das System durch irgendwelche Störungen leicht aus dem Gleichgewicht gebracht werden, nehme ich an.
| Zitat: | | Wenn die positive Ladung größer als jede negative Ladung ist, befindet sich das System nicht im statischen Gleichgewicht, es sei denn die negativen Eckladungen würden an ihren Positionen durch irgendeine Vorrichtung festgehalten werden. Anderenfalls würden sie sich auf die positive Ladung zubewegen, da die Anziehungskraft zwischen der mittleren Ladung und jeder Eckladung größer ist als die Summe der beiden abstoßenden Kräfte auf jede Eckladung. |
Wenn dann wie gesagt die pos. Ladung größer als jede neg. Ladung ist, dann ist die Gesamtkraft der jeweiligen hellblauen Pfeile(Abstoßkräfte) kleiner, als die Anziehungskraft(grün=blau) und somit würde die pos. Ladung alle 3 neg. Ladungen anziehen.
| Zitat: |
Um in Deinem Bild zu bleiben: Jede der drei grünen Kräfte wäre kleiner als die Summe aller drei blauen Kräfte auf eine Eckladung. Die positive Ladung wäre zwar im Gleichgewicht (sofern die drei Eckladungen gleich groß sind), die negativen Ladungen würden sich aber von der Mittenladung wegbewegen, d.h. das System befände sich nicht in einem statischen Gleichgewicht.
|
Nun ist es umgekehrt: Die einzelnen neg. Ladungen sind größer als die pos. Ladung.
Da nun die neg. Ladungen größer sind, muss die Gesamtkraft der hellblauen Pfeile größer sein, als die Anziehungskraft.
Diese zwei Fallunterschiede basieren auf dem Coulomb'schen Gesetz: 
Um mich nochmal auf die Ladungen im Bild zu beziehen:
- q1,q2,q3 > q4: Abstoßungskraft muss größer sein, da z.B. gilt: q1*q2 > q1*q4 (der restliche Term im obigen Gesetz ist ja konstant) und dasselbe mit dem Rest. (Wobei man bemerken muss, dass für gesamte Abstoßungskraft die hellblauen Vektoren addiert werden müssen)
- q1,q2,q3 < q4: Wie schon gesagt, umgekehrt: q1*q2 < q1*q4
Ich denke so müsste es passen und so klingt es auch logischer - ich habe in meinen letzten Beitrag das Coulumb'sche Gesetz nicht richtig angewandt.
| Beschreibung: |
|
| Dateigröße: |
6.97 KB |
| Angeschaut: |
5797 mal |
|
|
|
|
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
| mister Verfasst am: 01. Sep 2016 17:48 Titel: |
|
|
Könnte einer bitte noch Bestätigen zur Sicherheit, ob das alles jetzt so stimmt? (bzw. bei Fehlern kommentieren bitte) Danke  .
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 02. Sep 2016 00:19 Titel: |
|
|
| mister hat Folgendes geschrieben: | Um mich nochmal auf die Ladungen im Bild zu beziehen:
- q1,q2,q3 > q4: Abstoßungskraft muss größer sein, da z.B. gilt: q1*q2 > q1*q4 ... |
Das alleine reicht nicht. Die vektorielle Summe der Abstoßungskräfte infolge q2 und q3 muss größer sein als die Anziehungskraft zwischen q1 und q4. Du hast in Deiner Überlegung die Ladung q3 unberücksichtigt gelassen. Außerdem gilt das so pauschal nur, wenn q1=q2=q3. Anderenfalls ist - unabhängig von der absoluten Größe der Ladungen - das System sowieso nicht mehr im Gleichgewicht, da die Summe der abstoßenden Kräfte nicht mehr radial gerichtet ist (von q4 aus gesehen).
Ansonsten sehen Deine Überlegungen ziemlich richtig aus.
Im Übrigen solltest Du, wie von mir bereits vorgeschlagen, mal die Summe der abstoßenden Kräfte allgemein berechnen (nach Betrag und Richtung) und mit der anziehenden Kraft vergleichen, um zu erkennen, warum ein Gleichgewicht nur dann herrscht, wenn alle vier Ladungen denselben Betrag haben.
|
|
|
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
| mister Verfasst am: 03. Sep 2016 14:14 Titel: |
|
|
Danke.
Die Summe der abstoßenden Kräfte?
(F_xy=Kraft zwischen Ladung x und Ladung y)
Betrachten wir erstmal q3. Auf die wirkt F_13 und F_23. Ich kann nun F_12 parallel zu den Spitzen von F_13 und F_23 verschieben.
Naja hier sieht man deutlich, dass sich das Kräftedreieck nicht aufheben kann. Aber ich verstehe nicht, was ich daraus sehen soll.
Folgendes ist mir klar:
 (also grüner pfeil ist immer gleich dem entgegensetzten blauen Pfeil, gilt für alle anderen Ladungen auch) Auch z.B.  etc.
 :
 weil  > C\cdot q_3q_4 )
Und das gilt halt jetzt für die 2 anderen "Ecken" auch. So meinte ich das eigentlich in meinem letzten Beitrag, aber ich habs auch nicht genau hingeschrieben, sorry.
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 04. Sep 2016 12:17 Titel: |
|
|
| mister hat Folgendes geschrieben: |
Die Summe der abstoßenden Kräfte? |
Nein, die vektorielle Summe der abstoßenden Kräfte.
Deshalb ist das hier auch falsch:
| mister hat Folgendes geschrieben: | ...
:
weil |
Du hast hier den Vektorcharakter der Kräfte unberücksichtigt gelassen. Nach Deiner Rechnung wäre das System bei gleichen Ladungsbeträgen nämlich gar nicht im Gleichgewicht, sondern die Summe der abstoßenden Kräfte wäre doppelt so groß wie die anziehende Kraft.
Ich empfehle Dir deshalb zum wiederholten Male, den Betrag der vektoriellen Summe der abstoßenden Kräfte explizit zu berechnen und mit dem Betrag der anziehenden Kraft zu vergleichen. Dazu musst Du natürlich zuvor erkannt haben, dass die Summe der abstoßenden Kräfte um 180° gegen die anziehende Kraft gedreht ist (sonst könnte es ja auch kein Gleichgewicht geben). Nimm zur Hilfestellung mal Deine eigene Skizze.
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 04. Sep 2016 12:54 Titel: |
|
|
Ach ja, noch etwas:
| mister hat Folgendes geschrieben: | | Betrachten wir erstmal q3. Auf die wirkt F_13 und F_23. Ich kann nun F_12 parallel zu den Spitzen von F_13 und F_23 verschieben. |
Bei der Betrachtung der Kraft auf q3 hat die Kraft F_12 nichts zu suchen.
Ich befürchte, Du weißt selber nicht, wovon Du redest, und kann nur hoffen, dass ich Dir mit dieser Bemerkung nicht auf den Schlips trete.
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 04. Sep 2016 13:46 Titel: |
|
|
Oh, ich muss mich tausendmal entschuldigen. Denn meine Behauptung, das System sei bei 4 gleichen Ladungsbeträgen im Gleichgewicht ist falsch. Ich hatte das anfangs nur ganz schnell im Kopf gerechnet und mich dabei um den Faktor  verrechnet.
Nach wie vor ist richtig, dass q4 dann im Gleichgewicht ist, wenn alle drei Eckenladungen gleich groß sind (unabhängig davon, ob sie alle positiv oder alle negativ sind).
Die äußeren negativen Ladungen sind aber nur dann im Gleichgewicht, wenn ihr Betrag um den Faktor größer ist als der der mittleren positiven Ladung. Ich bin drauf gekommen, als ich jetzt endlich selber mal das schriftlich gerechnet habe, was ich Dir mehrfach vorgeschlagen hatte. Tut mir schrecklich leid für die Verwirrung, die ich möglicherweise gestiftet hbe.
Mein Rechenfehler ändert aber nichts daran, dass Du bislang immer noch eine falsche Vorstellung davon hast, wie die abstoßenden Kräfte auf die Eckladungen sich zusammensetzen.
|
|
|
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 05. Sep 2016 17:11 Titel: |
|
|
| mister hat Folgendes geschrieben: | ...
 und Betrag:
 |
Das ist nicht richtig. Rechne lieber nochmal nach.
| mister hat Folgendes geschrieben: | Und  und  |
Das sieht so aus, als sei die Konstante C bei beiden Kräften dieselbe. Das ist nicht der Fall. Kannst Du mal sagen, wie groß das C in den beiden Fällen ist?
| mister hat Folgendes geschrieben: | | Ich denke ich habs jetzt verstanden, nur weiß nicht wie du auf Wurzel 3 gekommen bist, denn bei mir ist es dasselbe nur ein Viertel davon. |
Wenn Du die oben angedeuteten Fehler korrigiert hast, wirst Du erkennen, warum Deine Lösung nicht richtig ist.
|
|
|
mister
Anmeldungsdatum: 23.08.2016
Beiträge: 51
|
| mister Verfasst am: 05. Sep 2016 19:03 Titel: |
|
|
Danke, es ist ganz klar  .
Stimmt, die Konstanten sind tatsächlich nicht gleich, da der Abstand ein anderer ist.
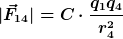
 , der Abstand zwischen q1 und q3, die Seitenlänge vom Dreieck.
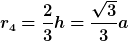 , wobei h die Höhe des gleichseitigen Dreiecks ist.
Beim Vergleich ist dann  und wenn  ist, dann ist die Bedingung erfüllt.
Wobei auch sein könnte, richtig?
|
|
|
|
|
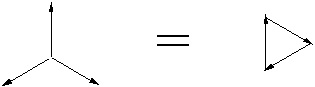
Registrieren
Login
FAQ
Suchen
