| Autor |
Nachricht |
Kaiuwe
Gast
|
 Kaiuwe Verfasst am: 29. Jun 2011 18:02 Titel: Elektrisches Feld im homogen geladenen Hohlzylinder Kaiuwe Verfasst am: 29. Jun 2011 18:02 Titel: Elektrisches Feld im homogen geladenen Hohlzylinder |
 |
|
Für die Ladungsverteilung in einem Hohlzylinder gilt:
Die Ladungsdichte p(r) = 0 für r<a, p(r) = p für a<r<b und p(r) = 0 für r>b. Wobei a der Innenradius und b der Außenradius des Hohlzylinders ist. Berechnen Sie das elektrische Feld entlang der r-Achse, für die 3 angegebenen Bereiche. So für r<a ist E=0, das weiß ich bereits. Für die anderen beiden Bereiche wäre mein Ansatz das Gesetz von Gauß anzuwenden.
Allerdings komme ich nicht wirklich klar. Deswegen hoffe ich hier etwas auf Hilfe:) |
|
 |
Niels90
Anmeldungsdatum: 02.07.2011
Beiträge: 280
|
 Niels90 Verfasst am: 02. Jul 2011 13:02 Titel: Niels90 Verfasst am: 02. Jul 2011 13:02 Titel: |
 |
|
Also ich hätte einen ersten Ansatz:
 \cdot dV)
So aber da fehlt immer noch die rechte Seite, dort muss dann wahrscheinlich etwas in Abhängigkeit von r dargestellt werden. Hat da jemand noch Ansätze? |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 03. Jul 2011 07:49 Titel: schnudl Verfasst am: 03. Jul 2011 07:49 Titel: |
 |
|
Der Satz von Gauss ist hier goldrichtig, nur musst du eben ein variables r nehmen und dieses nicht mit r=b festnageln. Mache eine Skizze !
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
Niels90

Anmeldungsdatum: 02.07.2011
Beiträge: 280
|
 Niels90 Verfasst am: 03. Jul 2011 10:35 Titel: Niels90 Verfasst am: 03. Jul 2011 10:35 Titel: |
 |
|
|
Ok alles klar. Das habe ich mir auch so in etwa schon überlegt, eben weil ja etwas in Abhängigkeit von r gefragt ist. So und jetzt aber die reche Seite. Ich hab echt nicht so richtig Plan wie ich das mit dem Volumenintegral und der Ladungsdichte angehen soll...Man könnte einfach das Volumenelement in Zylinderkoordinaten nehmen, aber ich weiß nicht ob das zum Ziel führen würde. |
|
 |
Niels90

Anmeldungsdatum: 02.07.2011
Beiträge: 280
|
 Niels90 Verfasst am: 03. Jul 2011 10:58 Titel: Niels90 Verfasst am: 03. Jul 2011 10:58 Titel: |
 |
|
Ok also um das nochmal zusammenfassend zu sagen:
Bisher hätte ich dann raus:
\cdot dV}{\epsilon_{0}\cdot 2\pi \cdot h\cdot r} ) |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 03. Jul 2011 18:16 Titel: GvC Verfasst am: 03. Jul 2011 18:16 Titel: |
 |
|
|
Jetzt musst Du nur noch das richtige Volumenelement dV einsetzen. |
|
 |
Niels90

Anmeldungsdatum: 02.07.2011
Beiträge: 280
|
 Niels90 Verfasst am: 03. Jul 2011 18:22 Titel: Niels90 Verfasst am: 03. Jul 2011 18:22 Titel: |
 |
|
Ja da würde ich sagen  , eben das Volumenelement in Zylinderkoordinaten. , eben das Volumenelement in Zylinderkoordinaten.
So also würde dann am Ende rauskommen:

Erscheint mir irgendwie falsch, bzw. zu einfach. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 04. Jul 2011 00:07 Titel: GvC Verfasst am: 04. Jul 2011 00:07 Titel: |
 |
|
Denk' an die Aufgabenstellung. Da ist von drei Bereichen die Rede.
In der Aufgabenstellung fehlt übrigens die Angabe der Materialeigenschaft der Rohrwandung. Da es sich offensichtlich um einen nichtleitenden Feststoff handelt, muss er eine DZ größer als 1 haben. |
|
 |
Niels90

Anmeldungsdatum: 02.07.2011
Beiträge: 280
|
 Niels90 Verfasst am: 04. Jul 2011 13:42 Titel: Niels90 Verfasst am: 04. Jul 2011 13:42 Titel: |
 |
|
Mhm dann vielleicht so:
 dV }{\epsilon _{0}\cdot 2\pi \cdot r\cdot h} + \frac{\int_a^b \varrho (r) dV }{\epsilon _{0}\cdot 2\pi \cdot r\cdot h}+ \frac{\int_b^\infty \varrho (r) dV }{\epsilon _{0}\cdot 2\pi \cdot r\cdot h}) |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 04. Jul 2011 13:48 Titel: GvC Verfasst am: 04. Jul 2011 13:48 Titel: |
 |
|
Nee, das darfst Du nicht addieren. Du musst jeden Bereich getrennt betrachten. Denk' an den Gaußschen Flusssatz. Welche Ladung wird von einem gedachten Hüllzylinder mit dem Radius r eingeschlossen. Das ist in den drei Bereichen unterschiedlich.
Außerdem musst Du im Bereich a<r<b die Permeabilitätszahl 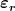 berücksichtigen. berücksichtigen. |
|
 |
Niels90

Anmeldungsdatum: 02.07.2011
Beiträge: 280
|
 Niels90 Verfasst am: 04. Jul 2011 13:58 Titel: Niels90 Verfasst am: 04. Jul 2011 13:58 Titel: |
 |
|
Ok neuer Versuch:)
 dV\cdot \frac{1}{2\pi \cdot r\cdot h\cdot \epsilon _{0} } =0)
Aber für das zweite Integral fehlt mir irgendwie ein Geistesblitz... |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 04. Jul 2011 15:49 Titel: GvC Verfasst am: 04. Jul 2011 15:49 Titel: |
 |
|
| Niels90 hat Folgendes geschrieben: | Ok neuer Versuch:)
 dV\cdot \frac{1}{2\pi \cdot r\cdot h\cdot \epsilon _{0} } =0)
Aber für das zweite Integral fehlt mir irgendwie ein Geistesblitz... |
Du sollst doch nicht nut die Feldstärke an der Stelle a bestimmen, sondern an allen Stellen 0<r<a. Also musst du von 0 bis r integrieren. Aber warum so kompliziert? Der Gaußsche Flusssatz lautet doch

Jetzt brauchst Du nur zu schauen, welche Ladung von einem (gedachten) Zylinder mit dem Radius r eingeschlossen wird. Die ist im Bereich 0<r<a natürlich Null, also ist auch die Feldstärke im gesamten Bereich 0<r<a Null. Das hast Du zwar auch rausbekommen, aber nur für die Stelle r=a.
Für den zweiten Bereich a<r<b ist die eingeschlossene Ladung von r abhängig:
 =\int_a^r \rho\,dV)
Wenn Du das in die Feldstärkegleichung einsetzt, musst Du berücksichtigen dass 
Und im dritten Beeich ist die eingeschlossene Ladung unabhängig von r immer dieselbe, nämlich

Da Du Dich da wieder in Luft befindest, ist  . . |
|
 |
Niels90

Anmeldungsdatum: 02.07.2011
Beiträge: 280
|
 Niels90 Verfasst am: 04. Jul 2011 17:47 Titel: Niels90 Verfasst am: 04. Jul 2011 17:47 Titel: |
 |
|
Ok also nur nochmal für mich zum Verständnis:
r<a ist klar, da ist keine Ladung vorhanden, deswegen auch keine Feldstärke.
Im Bereich a<r<b nimmt die Ladung linear mit dem Abstand zu, sprich je weiter nach außen man geht umso höher ist die Ladung und umso größer ist auch die elektrische Feldstärke.
Und im letzten Bereich hat man dann die Ladung Q, allerdings entfernt man sich vom "Zentrum" sodass das E~1/r abfällt oder? |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 04. Jul 2011 18:15 Titel: GvC Verfasst am: 04. Jul 2011 18:15 Titel: |
 |
|
| Lupoo hat Folgendes geschrieben: | | Im Bereich a<r<b nimmt die Ladung linear mit dem Abstand zu ... |
Na ja, so einfach ist es nun doch nicht. Denk' dran, dass
1. nicht von 0 bis r, sondern von a bis r integriert wird
2. das Integralzeichen nicht vor den Bruchstrich, sondern auf dem Bruchstrich steht |
|
 |
Niels90

Anmeldungsdatum: 02.07.2011
Beiträge: 280
|
 Niels90 Verfasst am: 04. Jul 2011 18:24 Titel: Niels90 Verfasst am: 04. Jul 2011 18:24 Titel: |
 |
|
Oh man, ich glaub heute ist nicht mein Tag:(
Also nochmal für a<r<b

Gilt natürlich nur bis r=b.
Oder hängts da jetzt wieder irgendwo? |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 04. Jul 2011 18:34 Titel: GvC Verfasst am: 04. Jul 2011 18:34 Titel: |
 |
|
| Niels90 hat Folgendes geschrieben: | Oh man, ich glaub heute ist nicht mein Tag:(
Also nochmal für a<r<b

Gilt natürlich nur bis r=b.
Oder hängts da jetzt wieder irgendwo? |
Es hängt wieder. Du hast meine beiden Hinweise nicht berücksichtigt! |
|
 |
Niels90

Anmeldungsdatum: 02.07.2011
Beiträge: 280
|
 Niels90 Verfasst am: 04. Jul 2011 19:02 Titel: Niels90 Verfasst am: 04. Jul 2011 19:02 Titel: |
 |
|
Stimmt, wie gesagt heute ist nicht mein Tag...
Dann so:
}{2\cdot \epsilon _{0}\cdot \epsilon _{r} \cdot r } )
Bitte sag mir dass es diesmal stimmt:) |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 04. Jul 2011 20:24 Titel: GvC Verfasst am: 04. Jul 2011 20:24 Titel: |
 |
|
|
Diesmal stimmt's, und das ist kein linearer Anstieg der Feldstärke mit r. |
|
 |
Niels90

Anmeldungsdatum: 02.07.2011
Beiträge: 280
|
 Niels90 Verfasst am: 04. Jul 2011 20:26 Titel: Niels90 Verfasst am: 04. Jul 2011 20:26 Titel: |
 |
|
|
Super vielen Dank dann an dieser Stelle, hast mir sehr geholfen:) |
|
 |
|















