| Autor |
Nachricht |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 03. März 2021 23:22 Titel: Elektrisches Feld Dexter33 Verfasst am: 03. März 2021 23:22 Titel: Elektrisches Feld |
 |
|
Hey Leute wie zeichne ich das bei der a)?
Meine Idee wäre das es bis r1 eine horizontale ist und wie verläuft das genau von r1 bis r2 ( 2 Bereich)?
Hat jemand eine Idee ?
Zuletzt bearbeitet von Dexter33 am 08. März 2021 07:57, insgesamt einmal bearbeitet |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 04. März 2021 08:14 Titel: Myon Verfasst am: 04. März 2021 08:14 Titel: |
 |
|
Ja, im innersten Bereich  ist die Raumladungsdichte konstant, ist die Raumladungsdichte konstant, =\rho_0) . Ab da nimmt sie linear ab von . Ab da nimmt sie linear ab von =\rho_0) bis bis =0) . .
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 04. März 2021 12:45 Titel: GvC Verfasst am: 04. März 2021 12:45 Titel: |
 |
|
| Dexter33 hat Folgendes geschrieben: | | Würdest du bei der b) zustimmen ? |
Unter b) ist nicht nach der Verschiebungsdichte D gefragt, sondern nach der Gesamtladung in den drei Raumgebieten.
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 04. März 2021 13:10 Titel: Dexter33 Verfasst am: 04. März 2021 13:10 Titel: |
 |
|
Soll ich bei der b) nicht den Gaußschen Satz anwenden ?
Q= Integral D*dA ?
Ist es D*2pi*r1^2 ?
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 04. März 2021 13:23 Titel: Myon Verfasst am: 04. März 2021 13:23 Titel: |
 |
|
Um D(r) zu kennen, musst Du zuerst die Ladung Q(r) kennen, die in einer Kugel mir Radius r ein geschlossen ist. In b) muss ja die Gesamtladung im inneren und im daran anschliessenden Bereich r1<r<r2 bestimmt werden. Dazu die Ladungsdichte integrieren, im 1. Fall z.B.
r^2\,\dd r)
-was hier einfach ist, da in diesem Bereich ) konstant ist. konstant ist.
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 04. März 2021 17:10 Titel: Dexter33 Verfasst am: 04. März 2021 17:10 Titel: |
 |
|
r^2\,\dd r)

Würde das so stimmen ?
Wie integriere ich das im zweiten Fall ?
Gibt es da einen Trick ?
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 05. März 2021 11:32 Titel: Dexter33 Verfasst am: 05. März 2021 11:32 Titel: |
 |
|
Wie kann ich den Term von r1 bis r2 integrieren ?
Der Term ist komplizierter
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 05. März 2021 12:29 Titel: Myon Verfasst am: 05. März 2021 12:29 Titel: |
 |
|
Habe Deinen gestrigen Beitrag übersehen...
| Dexter33 hat Folgendes geschrieben: | 
Würde das so stimmen ? |
Ja, einfach mit 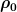 statt statt 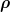 : :

| Zitat: | Wie integriere ich das im zweiten Fall ?
Gibt es da einen Trick ? |
Genauso, wie im ersten Fall:
r^2\,\dd r=\frac{4\pi\rho_0}{r_2-r_1}\int\limits_{r_1}^{r_2}(r_2r^2-r^3)\,\dd r)
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 05. März 2021 18:16 Titel: Dexter33 Verfasst am: 05. März 2021 18:16 Titel: |
 |
|
Das Ergebnis zum zweiten Teil:

Weiss nicht ob man das vereinfachen kann 
Habt ihr Experten auch tipps zu der c) ? 
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 05. März 2021 20:56 Titel: Myon Verfasst am: 05. März 2021 20:56 Titel: |
 |
|
Ich erhalte

Aber ich habe das nicht lange überprüft, es ist sehr gut möglich, dass es nicht korrekt ist. Auf alle Fälle müssen in allen Summenden insgesamt die gleichen Potenzen von r1, r2 vorkommen.
In Aufgabenteil c) genau gleich vorgehen, aber jetzt bis r integrieren. Es ist dann eine Fallunterscheidung zu machen, etwa so:
=\left\{\begin{array}{ll}... &\quad r\leq r_1\\... &\quad r_1< r\leq r_2\\... &\quad r>r_2\end{array}\right.)
Beim Fall  müsste man also rechnen müsste man also rechnen
=\frac{4\pi\rho_0}{r_2-r_1}\int\limits_0^r \rho(r')r'^2\,\dd r')
Beim zweiten Fall,  dann dann
=Q(r_1)+\frac{4\pi\rho_0}{r_2-r_1}\int\limits_{r_1}^r \rho(r')r'^2\,\dd r')
Dabei ist ) natürlich gleich dem bereits in b) berechneten natürlich gleich dem bereits in b) berechneten 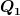 . .
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 06. März 2021 03:49 Titel: Dexter33 Verfasst am: 06. März 2021 03:49 Titel: |
 |
|
In Aufgabenteil c)
=\left\{\begin{array}{ll}... &\quad r\leq r_1\\... &\quad r_1< r\leq r_2\\... &\quad r>r_2\end{array}\right.)
Beim Fall  müsste man also rechnen müsste man also rechnen
=\frac{4\pi\rho_0}{r_2-r_1}\int\limits_0^r \rho(r')r'^2\,\dd r' =1/3*r^3)
Beim zweiten Fall,  dann dann
=Q(r_1)+\frac{4\pi\rho_0}{r_2-r_1}\int\limits_{r_1}^r \rho(r')r'^2\,\dd r' = 1/3 r -1/3*r1)
Das wären meine Ergebnisse ?
Aber verstehe nicht warum man bei c) nur r^2 integriert ?
Verstehe das nicht .
Soll ich jetzt bei d) den Gaußschen Satz anwenden :
Q = Integral D*dA?
Und für die Fläche 4pir^2 einsetzen ?
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 06. März 2021 07:26 Titel: Myon Verfasst am: 06. März 2021 07:26 Titel: |
 |
|
Nur ganz kurz:
| Dexter33 hat Folgendes geschrieben: | Aber verstehe nicht warum man bei c) nur r^2 integriert ?
Verstehe das nicht . |
Im Integrand steht doch r'^2) ? ?
| Zitat: | Soll ich jetzt bei d) den Gaußschen Satz anwenden :
Q = Integral D*dA?
Und für die Fläche 4pir^2 einsetzen ? |
Ja, das Gausssche Gesetz benutzen. Auf der linkekn Seite der Gleichung steht Q(r), und dann wieder die 3 Fälle unterscheiden.
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 06. März 2021 11:42 Titel: Dexter33 Verfasst am: 06. März 2021 11:42 Titel: |
 |
|
d)
 = \int_a^b \! D \, \dd A = D*4\pi *r^2 )

}{4\pi *r^2} )
eingesetzt:

Wie berechne ich das D2 ? 
Wirkt schon kompliziert
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 06. März 2021 14:22 Titel: Myon Verfasst am: 06. März 2021 14:22 Titel: |
 |
|
In d) ist ) gesucht für ein beliebiges gesucht für ein beliebiges 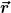 . Aus Symmetriegründen hat . Aus Symmetriegründen hat ) die Form die Form
=D(r)\vec{e}_r)
Um D(r) zu bestimmen, musst Du zuerst c) lösen. Dann für die 3 Bereiche jeweils
=4\pi r^2D(r))
setzen.
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 06. März 2021 15:07 Titel: Dexter33 Verfasst am: 06. März 2021 15:07 Titel: |
 |
|
[quote="Dexter33"]In Aufgabenteil c)
=\left\{\begin{array}{ll}... &\quad r\leq r_1\\... &\quad r_1< r\leq r_2\\... &\quad r>r_2\end{array}\right.)
Beim Fall  müsste man also rechnen müsste man also rechnen
=\frac{4\pi\rho_0}{r_2-r_1}\int\limits_0^r \rho(r')r'^2\,\dd r' =1/3*r^3)
Beim zweiten Fall,  dann dann
=Q(r_1)+\frac{4\pi\rho_0}{r_2-r_1}\int\limits_{r_1}^r \rho(r')r'^2\,\dd r' = 1/3 r -1/3*r1)
die c) habe ich doch hier oben gelöst ?
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 06. März 2021 15:17 Titel: Myon Verfasst am: 06. März 2021 15:17 Titel: |
 |
|
Nein, jedenfalls nicht richtig. Q(r)=r^3/3 ist doch keine Ladung. Du musst ) aus den jeweiligen Bereichen einsetzen und dann integrieren. aus den jeweiligen Bereichen einsetzen und dann integrieren.
Bitte jeweils die Zitate-Funktion oder quote-Umgebung verwenden, dann wird es übersichtlicher und man erkennt, wer was geschrieben hat.
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 06. März 2021 15:23 Titel: Dexter33 Verfasst am: 06. März 2021 15:23 Titel: |
 |
|
Beim Fall  müsste man also rechnen müsste man also rechnen
=\frac{4\pi\rho_0}{r_2-r_1}*[1/3*r^3] )
Beim zweiten Fall,  dann dann
=Q(r_1)+\frac{4\pi\rho_0}{r_2-r_1}*[ 1/3 r -1/3*r1])
Das wäre es richtig oder ?
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 06. März 2021 15:33 Titel: Myon Verfasst am: 06. März 2021 15:33 Titel: |
 |
|
Bitte entschuldige, was ich oben zu c) geschrieben habe, ist grundsätzlich schon richtig, aber die Integrale sind falsch. Es muss das ) integriert werden, das in der Aufgabenstellung gegeben ist. Weiss nicht, was ich da überlegt habe. Bin nun einige Zeit abwesend, melde mich dann wieder. integriert werden, das in der Aufgabenstellung gegeben ist. Weiss nicht, was ich da überlegt habe. Bin nun einige Zeit abwesend, melde mich dann wieder.
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 06. März 2021 16:39 Titel: Dexter33 Verfasst am: 06. März 2021 16:39 Titel: |
 |
|
hi MYon,
Kannst du wenn du zurück bist erklären wie du das dann genau meinst ?
Bin jetzt auch verwirrt 
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 06. März 2021 17:34 Titel: Myon Verfasst am: 06. März 2021 17:34 Titel: |
 |
|
Grundsätzlich ist Q(r) einfach die bis r aufintegrierte Ladungsdichte 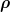 : :
=4\pi \int\limits_0^r\rho(r')r'^2\,dr)
Setzt man für die 3 Bereiche die gegebene Ladungsdichte ein, erhält man (nachprüfen, ohne jede Gewähr...)
-für  : :
=\frac{4\pi}{3}\rho_0r^3)
-für  : :
=Q(r_1)+\frac{4\pi\rho_0}{r_2-r_1}\int\limits_{r_1}^r(r_2-r')r'^2\,dr)
-\frac{1}{4}(r^4-r_1^4)\right])

-für  : :
=Q(r_2)=\frac{\pi\rho_0}{3(r_2-r_1)}(r_2^4-r_1^4))
Zusammengefasst also
=\begin{cases}\frac{4\pi}{3}\rho_0r^3 &\quad r\leq r_1\\ \frac{4\pi\rho_0}{r_2-r_1}\left[\frac{1}{3}r_2r^3-\frac{1}{4}r^4-\frac{1}{12}r_1^4\right] &\quad r_1\leq r\leq r_2\\ \frac{\pi\rho_0}{3(r_2-r_1)}(r_2^4-r_1^4) &\quad r>r_2 \end{cases})
Q(r) muss sicher stetig sein, und das sollte mit dem oben angegebenen Verlauf erfüllt sein.
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 06. März 2021 18:52 Titel: Dexter33 Verfasst am: 06. März 2021 18:52 Titel: |
 |
|
d)
Ich poste mal meinen Ansatz für den ersten Fall .
ich weiss nicht ob das quatsch ist ,aber poste es :
Habe meine Rechnung im Bild angehängt .
?
| Beschreibung: |
|

Download |
| Dateiname: |
Bildschirmfoto 2021-03-06 um 18.51.59.png |
| Dateigröße: |
602.27 KB |
| Heruntergeladen: |
153 mal |
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 07. März 2021 13:33 Titel: Nils Hoppenstedt Verfasst am: 07. März 2021 13:33 Titel: |
 |
|
Moin,
das ist noch nicht ganz richtig. Links ist einfach die radiusabhängige Gesamtladung Q(r) zu nehmen und auf der rechten Seite muss das Flächenintegral berechnet werden. Nicht das Volumenintegral.
Viele Grüße,
Nils
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 07. März 2021 13:57 Titel: Dexter33 Verfasst am: 07. März 2021 13:57 Titel: |
 |
|
Q(r) = D*dA
Q = D*4pi*r^2
meinst du es so?
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 07. März 2021 14:34 Titel: Dexter33 Verfasst am: 07. März 2021 14:34 Titel: |
 |
|
Aber wie mache ich das dann für die anderen Bereiche ?
Dachte das man das für die anderen Bereiche irgendwie machen soll?
Aber das verwirrt mich auch 
Wenn ich auf der linken Seite nur Q einsetzen soll ,dann bin ich ja eigentlich schon fertig damit .
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 07. März 2021 15:17 Titel: Myon Verfasst am: 07. März 2021 15:17 Titel: |
 |
|
D(r) ist für alle Bereiche gegeben durch
=\frac{Q(r)}{4\pi r^2})
Einfach das für jeden Bereich „ausrechnen“, und der gesuchte Vektor D ist dann jeweils
=D(r)\vec{e}_r)
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 07. März 2021 15:20 Titel: Nils Hoppenstedt Verfasst am: 07. März 2021 15:20 Titel: |
 |
|
Ja, die verschiedenen Bereiche sind bereits in Q(r) berücksichtigt und wurde bereits von Myon berechnet (siehe oben). Das kannst du jetzt benutzen, um D(r) darzustellen.
- Nils
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 07. März 2021 16:51 Titel: Dexter33 Verfasst am: 07. März 2021 16:51 Titel: |
 |
|
|
Soll ich für Q jetzt die einzelnen Terme einsetzen und fertig ?
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 07. März 2021 19:22 Titel: Nils Hoppenstedt Verfasst am: 07. März 2021 19:22 Titel: |
 |
|
|
Ja. Ich glaube, der Hauptzweck dieser Aufgabe ist einfach zu verstehen, warum man das D-Feld in diesem Fall direkt so einfach hinschreiben kann. Das liegt letztendlich an der Kugelsymmetrie des Problems.
|
|
 |
Dexter33
Anmeldungsdatum: 07.08.2020
Beiträge: 138
|
 Dexter33 Verfasst am: 07. März 2021 20:06 Titel: Dexter33 Verfasst am: 07. März 2021 20:06 Titel: |
 |
|
Das ist mein Ergebnis zur d)
Richtig?
| Beschreibung: |
|

Download |
| Dateiname: |
Bildschirmfoto 2021-03-07 um 20.05.30.png |
| Dateigröße: |
951.11 KB |
| Heruntergeladen: |
139 mal |
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 07. März 2021 22:58 Titel: Myon Verfasst am: 07. März 2021 22:58 Titel: |
 |
|
Doch, das kann man so schreiben. Auf der linken vom Seite vom Gleichheitszeichen bei D und r noch ein Vektorpfeil drauf.
Als Lösung ist die Notation so nicht optimal, denn es handelt sich um ein Vektorfeld ) , einfach für verschiedene Bereiche von , einfach für verschiedene Bereiche von 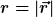 . Ich würde die Lösung so angeben wie Q(r) weiter oben. . Ich würde die Lösung so angeben wie Q(r) weiter oben.
|
|
 |
|


















