| Autor |
Nachricht |
Norbert
Gast
|
 Norbert Verfasst am: 04. Jul 2005 22:54 Titel: Magnetfeld/Stromdichte im Hohlzylinder Norbert Verfasst am: 04. Jul 2005 22:54 Titel: Magnetfeld/Stromdichte im Hohlzylinder |
 |
|
Hallo zusammen,
ich zerbreche mir schon seit einiger Zeit den Kopf über eine Elektrophysik Aufgabe.
Ein leitender Hohlzylinder (R_i = 1cm, R_a =2cm) werde in z-Richtung (also im inneren des Hohlzylinders) von einem elektrischen Strom I = 10A durchflossen.
a) Welche Stromstärke ergibt sich im Hohlzylinder?
b) Wie groß ist das maximale Magnetfeld?
Jetzt habe ich erstmal mit 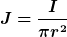
J_i und J_a berechnet.
Kann ich jetzt einfach die Stromdichte des Innenleiters von der Stromdichte des Außenleiters abziehen um die Stromdichte im Hohlzylinder zu bekommen?
Des weiteren habe ich gelesen das beim Koaxialkabel (ist ja hier daselbe Prinzip) das Feld des Innenleiter von der Anwesenheit des Außenleiters nicht beeinflusst wird! D.h. ich könnte das Feld mit der Formel
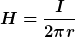
berechnen. Das würde ja weiterhin bedeuten, dass das Feld mit 1/r abnimmt und somit am Innenradius am größten wäre, oder?
Ich hoffe das ihr mir helfen könnt.
Gruß Norbert
|
|
 |
sax

Anmeldungsdatum: 10.05.2005
Beiträge: 377
Wohnort: Magdeburg
|
 sax Verfasst am: 05. Jul 2005 00:50 Titel: sax Verfasst am: 05. Jul 2005 00:50 Titel: |
 |
|
Ehrlich gesagt glaube ich dass du die Aufgabe falsch verstanden hast, oder du hast sie schlecht formuliert.
Du hast eine Stromstärke gegeben, mit der Gleichung:
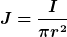
würdest du eine Stromdichte berechnen, allerdings die durch einen Vollzylinder. Die Stromdichte ist im Wesentlichen der Strom, der je Flächenelement durch eine Fläche, senkrecht zum Strom, fließt. Wenn du durch einen Zylinder eine Fläche legst, die Senkrecht zur Stromrichtung liegt,
ist diese ein Kreis. Wenn der Strom homogen in der Fläche verteilt ist, ist die Stromdichte die Stärke des Gesamtstromes durch diese Fläche. Die Fläche eines Kreises ist 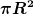 . Deshalb ist Die Stromdichte dann . Deshalb ist Die Stromdichte dann 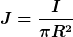 . Diese ist auf der ganzen Kreisfläche konstant, es ist nicht die Stromdichte beim Radius r. R ist hier der Radius des Zylinders, nicht die Koordinatenposition, an der du die Stromdichte kennen möchtest. . Diese ist auf der ganzen Kreisfläche konstant, es ist nicht die Stromdichte beim Radius r. R ist hier der Radius des Zylinders, nicht die Koordinatenposition, an der du die Stromdichte kennen möchtest.
Ich vermute eigentlich das die Aufgabe so gemeint ist, dass durch den leitenden Hohlzylinder, in der Zylinderwand, ein homogener Strom fließen soll, und du bei a) die Stromdichte im Zylinder Berechnen sollst. Das der Strom in z Richtung fließt heißt nicht, das er genau auf der z Achse fließt, sondern innerhalb der Zylinderwand halt in z Richtung.
Die Stromdichte ist dann die Gesamte Stromstärke durch die Querschnittsfläche der Leitenden anteile des Zylinders. Diese ist ein Kreisring mit Innenradius 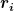 und Außenradius und Außenradius  , diese Fläche solltest du berechnen können. , diese Fläche solltest du berechnen können.
Für das Feld hast du schon die Richtige Gleichung aufgeschrieben:
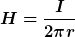 . Dies ist die Feldstärke beim Radius r, also ist r der Abstand vom Zylindermittelpunkt, bei dem du das Feld kennen möchtest, nicht etwa der Radius des Zylinders. . Dies ist die Feldstärke beim Radius r, also ist r der Abstand vom Zylindermittelpunkt, bei dem du das Feld kennen möchtest, nicht etwa der Radius des Zylinders.
I enthält allerdings nur den Strom, der insgesamt durch einen Kreis mit dem Radius r fließt.
Also für Radien, die kleiner sind als der Innenradius des Zylinders, fließt innerhalb durch einen Kreis mit diesem Radius überhaupt kein Strom, da ja nur im in der Zylinderwand ein Strom fließt.
Wenn du dir die Situation außerhalb des Zylinders anschaust ist I=10A, da. Der Radius deines Kreises ist nun größer als 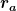 . Die Fläche dieses Kreises enthält nun die Gesamte Außenwand deines Zylinders. Deshalb ist der Strom durch diesen Kreis gleich dem Gesamtstrom. . Die Fläche dieses Kreises enthält nun die Gesamte Außenwand deines Zylinders. Deshalb ist der Strom durch diesen Kreis gleich dem Gesamtstrom.
Etwas schwieriger ist es, wenn du das Feld im inneren des Leiters anschaust. Wenn du einen Radius 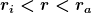 , enthält dein Kreis erstmal die Innenfläche, durch die kein Strom fließt, und einen Teil der Mantelfläche, durch die Strom fließt, dein I ist in diesem Fall vom Radius abhängig. Zum Glück haben wir aber am Anfang die Stromdichte berechnet. Du musst also nur noch vom Strom durchflossene Fläche mit der Stromdichte Multiplizieren, um I(r) zu erhalten: , enthält dein Kreis erstmal die Innenfläche, durch die kein Strom fließt, und einen Teil der Mantelfläche, durch die Strom fließt, dein I ist in diesem Fall vom Radius abhängig. Zum Glück haben wir aber am Anfang die Stromdichte berechnet. Du musst also nur noch vom Strom durchflossene Fläche mit der Stromdichte Multiplizieren, um I(r) zu erhalten:
Diese Fläche ist offenbar eine Kreisscheibe mit dem Innenradius 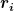 und dem Außenradius und dem Außenradius  . Also . Also
 )
Der durch diese Fläche fließende Strom ist:
 = J A = J \pi (r^2-r_i^2) )
Das Feld ist dann:
}{r} & r_i<r<r_a \cr \frac{10A}{\pi r^2} & r > r_a }} \right. )
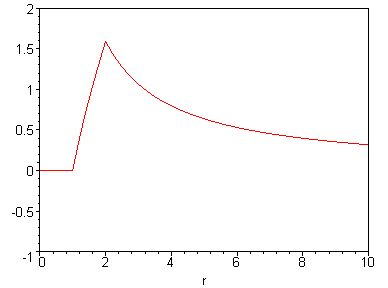
So jetzt habe ich die Aufgabe fast bis zum Schluss ausgex't, wenn du alles richtig gemacht hast sollte deine Kurve wie die Angehängte aussehen:
| Beschreibung: |
|
| Dateigröße: |
12 KB |
| Angeschaut: |
40421 mal |
|
|
|
 |
Norbert
Gast
|
 Norbert Verfasst am: 05. Jul 2005 11:51 Titel: Norbert Verfasst am: 05. Jul 2005 11:51 Titel: |
 |
|
Hallo Sax,
danke erstmal für die sehr ausführliche Bearbeitung meiner Aufgabe.
Nachdem ich nochmal über die Aufgabe drüber nachgedacht habe, könntest du recht haben, dass der Strom nur durch den Hohlzylinder fließt und die z-Achse nur die Richtung ist. Somit ist die Sache mit der Stromdichte klar.
Aber irgendwie habe ich mit deinen Formeln für die Feldstärke H ein Problem.
Weil in meinem Elektrophysik Script und in meiner Formelsammlung steht drin, dass ich die Feldstärke außerhalb eines Leiters mit
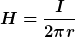
ausrechne. Und das Feld innerhalb eines Leiters mit
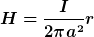
a ist hier der Leiterdurchmesser
Mit diesen Formel verstehe ich auch deine beigefügte Grafik.
D.h. bis zum Außendurchmesser nimmt das Feld mit r linear zu und mit r>r_a nimmt das Feld mit 1/r ab. Oder sehe ich das falsch?
Aber wie kommst du auf }{r})
|
|
 |
sax

Anmeldungsdatum: 10.05.2005
Beiträge: 377
Wohnort: Magdeburg
|
 sax Verfasst am: 05. Jul 2005 13:51 Titel: sax Verfasst am: 05. Jul 2005 13:51 Titel: |
 |
|
Deine Gleichung gilt wieder nur für Zylinderförmige Leiter.
Bei meiner Gleichung war aber ein 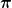 Zuviel. Wenn vdu einfach mal Zuviel. Wenn vdu einfach mal 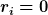 setzt, J und H ausrechest, kommst du wieder auf deine Gleichung. setzt, J und H ausrechest, kommst du wieder auf deine Gleichung.
Man kommt auf die Gleichung, über den Stok'schen satz, vieleicht schreib ich das heute Abend noch mal richtig auf.
|
|
 |
Norbert
Gast
|
 Norbert Verfasst am: 05. Jul 2005 14:15 Titel: Norbert Verfasst am: 05. Jul 2005 14:15 Titel: |
 |
|
Jo danke das wäre super.
Gruß Norbert
|
|
 |
Gast
|
 Gast Verfasst am: 06. Jul 2005 00:39 Titel: Gast Verfasst am: 06. Jul 2005 00:39 Titel: |
 |
|
Okay,
Eine der Maxwell-Gleichungen:
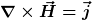
Das Integrieren wir über eine Kreisfläche mit dem Radius r, auf der rechten Seite ergibt sich:
 )
I(r) ist der Strom, der Insgesamt durch die Kreisfläche fließt, denn wenn man die Stromdichte über eine Fläche Integriert, kommt natürlich der Strom herraus, der insgesamt durch diese Fläche fließt. Schauen wir uns das Integral noch mal an, für  ist die Stromdichte Null, ansonsten ist sie konstant, wir können das Integral also getrost so schreiben: ist die Stromdichte Null, ansonsten ist sie konstant, wir können das Integral also getrost so schreiben:
 = I(r) )
und das ist gerade:
= \pi ( r^2-r_i^2) j )
j ist aber } ) , wobei , wobei 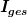 die 10 A sind. die 10 A sind.
Also:
= I_{ges} \frac{(r^2-r_i^2) }{(r_a^2-r_i^2)} ) , ,
das ist gerade das Verhältnis von unserer Kreisfläche, zur Fläche des Kreisringes, den der Schnitt durch den Hohlzylinder liefert mal I.
Jetzt haben wir erstmal
 ) Auf das Integral auf der linken Seite kann man den Stok'schen Satzt anwenden, dass Flächenintegral über die Rotation eines Vektorfeldes ist gleich dem Integral entlang dem Rand dieser Fläche über das Vektorfeld: Auf das Integral auf der linken Seite kann man den Stok'schen Satzt anwenden, dass Flächenintegral über die Rotation eines Vektorfeldes ist gleich dem Integral entlang dem Rand dieser Fläche über das Vektorfeld:
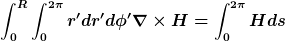 , Wegen der Symmetrie um den Mittelpunkt, und weil H nur in tangentialer Richtung zeigt, ist das der Kreisumfang mal H an bei diesem Radius. , Wegen der Symmetrie um den Mittelpunkt, und weil H nur in tangentialer Richtung zeigt, ist das der Kreisumfang mal H an bei diesem Radius.
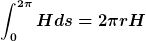
Fassen wir das mit dem oberen Ergebnis zusammen steht da:
 )
bzw.
}{2 \pi r} = I_{ges} \frac{(r^2-r_i^2) }{2 \pi r (r_a^2-r_i^2)} )
Das ist das alte Ergebnis, wenn man dort J ensetzt.
Wenn du jetzt mal Testweise 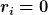 setzt, hast du: setzt, hast du:
 . .
Dies ist die Gleichung, die du angegeben hast.
|
|
 |
sax

Anmeldungsdatum: 10.05.2005
Beiträge: 377
Wohnort: Magdeburg
|
 sax Verfasst am: 06. Jul 2005 00:44 Titel: sax Verfasst am: 06. Jul 2005 00:44 Titel: |
 |
|
Sry, hatte vergessen mich einzuloggen,
noch ne kleine Anmerkung:
Das Feld ist bis zum Innenradius Null, dann steigt es bis zum Außenradius an, aber nicht ganz linear, sondern wie in der Gleichung angegeben, danach fällt es mit 1r ab.
|
|
 |
Norbert
Gast
|
 Norbert Verfasst am: 06. Jul 2005 12:04 Titel: Norbert Verfasst am: 06. Jul 2005 12:04 Titel: |
 |
|
Danke Sax,
das war glaube mehr als ausführlich.
Muss das ertmal verdauen. 
Was genau davon ist jetzt eigentlich der Stokessche Satz?
|
|
 |
ChrisP
Anmeldungsdatum: 06.07.2005
Beiträge: 1
|
 ChrisP Verfasst am: 06. Jul 2005 19:25 Titel: entgültige Gleichung? ChrisP Verfasst am: 06. Jul 2005 19:25 Titel: entgültige Gleichung? |
 |
|
Soweit so gut, aber welche ist nun die endgültige Gleichung für das max. Magnetfeld?
Es gilt in jedem Fall für r = r [aussen].
@sax: in deinem ersten Beitrag gibtst du Gleichungen für die Fälle r<r[innen]; r[innen]<r<r[aussen] und r[aussen]<r an. Wie ist nun das Magnetfeld für r=r[aussen] zu berechnen?
thx
ChrisP
|
|
 |
sunrise
Anmeldungsdatum: 11.06.2006
Beiträge: 1
|
 sunrise Verfasst am: 11. Jun 2006 18:34 Titel: Zylinderholraum in x-Richtung verschoben sunrise Verfasst am: 11. Jun 2006 18:34 Titel: Zylinderholraum in x-Richtung verschoben |
 |
|
Hallo Miteinander,
ich habe grade den ausführlichen threat überflogen und frage mich ob ich das richtig verstanden habe
| Anonymous hat Folgendes geschrieben: |
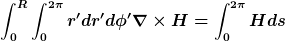 , Wegen der Symmetrie um den Mittelpunkt, und weil H nur in tangentialer Richtung zeigt, ist das der Kreisumfang mal H an bei diesem Radius. , Wegen der Symmetrie um den Mittelpunkt, und weil H nur in tangentialer Richtung zeigt, ist das der Kreisumfang mal H an bei diesem Radius. |
Wenn mein Zylinderholraum nicht im Ursprung des vorherigen Zylinders liegt, sondern um c in x-Richtung verschoben ist, dann kann ich diese Smmetrie überlegung nicht machen, oder?
Beste Grüße,
sunrise
|
|
 |
|
|

















