| Autor |
Nachricht |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
 TomS Verfasst am: 04. Nov 2014 10:53 Titel: Wahrscheinlichkeitsfluss in der Quantenmechanik |
 |
|
Mir ist aufgefallen, dass man im Falle von Interferenzexperimenten gerne mit der Wahrscheinlichkeitsdichte argumentiert. Eigtl. müsste man aber mit dem Wahrscheinlichkeitsfluss durch eine Oberfläche (den Schirm) argumentieren, d.h.
wobei j die Wahrscheinlichkeitsstromdichte
bezeichnet.
Wenn man nun ein zunächst lokalisiertes Wellenpaket betrachtet, müsste man eigtl. noch den Fluss über die Zeit integrieren, d.h.
Phi sollte dann mit der Intensitätsverteilung für einen kleinen Ausschnitt S des Schirms zusammenhängen. Grundsätzlich soll S völlig beliebig sein, d.h. insbs. auch nicht geschlossen.
Leider finde ich diesen Ausdruck nirgends und kann ihn auch nicht in irgendetwas mir Bekanntes umformen oder eine bekannte Beziehung (Kontinuitätsgleichung ...) anwenden.
Wäre für einen Hinweis dankbar; wahrscheinlich hab' ich Tomaten auf den Augen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 04. Nov 2014 12:03 Titel: |
|
|
nee; S ist keine Berandung eines Volumens V sondern beliebig
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 04. Nov 2014 12:04 Titel: |
|
|
|
Wieso sollte das so sein? Du willst ja ausrechnen, ob das Teilchen in einem bestimmten Volumen des Schirms wechselwirkt... |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 04. Nov 2014 12:07 Titel: |
|
|
Ich will wissen, wie das Teilchen eine Fläche S durchdringt, also die Wahrscheinlichkeit / Häufigkeit / Intenstität in der Fläche (dem Flächenelement) S.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 04. Nov 2014 12:39 Titel: |
|
|
|
Aber was für das Experiment von Bedeutung ist, ist ob das Teilchen in einem Volumenelement des Schirms wechselwirkt. Oder was möchtest Du ausrechnen? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 04. Nov 2014 13:20 Titel: |
|
|
Ich kann nicht berechnen, ob es im Schirm wechselwirkt, ich kann nur berechnen, ob es dort ist. Wenn ich jedoch annehme, dass der Schirm ein idealer Absporber ist, dann wird jedes Teilchen, das den Schirm durchdringt, auch mit diesem wechselwirken. Das führt mich auf die Definition des Flusses durch den Schirm.
Wenn ich statt stationären Lösungen reale Wellenpakete betrachte, dann muss ich den Fluss außerdem noch über die Zeit integrieren.
Nehmen wir an, ich habe ein stark lokalisiertes Wellenpaket, das ich durch einen Doppelspalt schicke. Das Interferenzmuster entspricht nun sicher nicht der Wsk.-dichte zu einem bestimmten Zeitpunkt, sondern sozusagen der "zeitlich integrierten Intensität". Wenn ich also die Schwärzung eines bestimmten (kleinen) Bereiches S berechnen möchte, dann muss ich doch intuitiv den Fluss durch S berechnen, also die "zeitlich integrierte Transmission". Das führt mich jetzt intikutiv auf die o.g. Ausdrücke.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 04. Nov 2014 13:25 Titel: |
|
|
| TomS hat Folgendes geschrieben: | Ich kann nicht berechnen, ob es im Schirm wechselwirkt, ich kann nur berechnen, ob es dort ist. Wenn ich jedoch annehme, dass der Schirm ein idealer Absporber ist, dann wird jedes Teilchen, das den Schirm durchdringt, auch mit diesem wechselwirken. Das führt mich auf die Definition des Flusses durch den Schirm.
|
Genau, d.h. "hinten" geht aus dem Schirm nichts raus, dort ist j=0 und du kannst Dein Integral über eine offene Flaeche in eins über eine geschlossene Fläche ändern, da die Beitrage verschwinden. Dann Satz von Gauss und man erhält den üblichen Ausdruck.
Ob das jetzt natürlicher ist, als von der W'keitsdichte zu starken weiss ich nicht.. vermutlich Geschmacksache, bzw Definition wie man in den theoretischen Annahmen den Messprozess mit der Wellenfunktion verknüpft. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 04. Nov 2014 13:40 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: | | ... und du kannst Dein Integral über eine offene Flaeche in eins über eine geschlossene Fläche ändern, da die Beitrage verschwinden. |
Sorry, ich bin zu blöd, ich versteh's nicht.
Wie soll den die Fläche aussehen?
Der Schirm sei die unendlich ausgedehnte xy-Ebene mit z=0. Die Fläche S, die mich interessiert, sei ein kleines Quadrat [a,a+L] * [b,b+L] in dieser Ebene. Wie berechne ich aus der Wellenfunktion oder dem Strom die Schwärzung? Wenn ich ein reales Wellenpaket betrachbte: muss ich dann zeitabhängige Streutheorie betreiben? Und wieder die selbe Frage, was integriere ich wie über die Zeit?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 04. Nov 2014 13:45 Titel: |
|
|
Du nimmst doch an, dass jedes Teilchen in dem Schirm absorbiert wird. D.h. j ist hinter dem Schirm 0, somit kannst Du einen kleinen Kasten von epsilon-dicke um den Schirm legen, mit Seiten parallel zum Schirm, einmal davor einmal dahinter.
Hier das entspreche Bild aus der E-Dynamik:
http://www.tutorhelpdesk.com/UserFiles/Electrostatic%20Boundary%20Conditions.jpg
Vllt versteh ich auch nicht ganz was Du ausrechnen willst, aber ich seh in dem Weg den ich gehen würde keine Probleme... |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 04. Nov 2014 13:53 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Wenn ich ein reales Wellenpaket betrachbte: muss ich dann zeitabhängige Streutheorie betreiben? Und wieder die selbe Frage, was integriere ich wie über die Zeit? |
Wenn Du die Schrotdinger-Gleichung für ein "Doppelspalt-Potential" explizit lösen willst, musst Du das vermutlich tun, oder numerisch...
Ich glaube hier wurde das gemacht:
http://link.springer.com/article/10.1007%2Fs10773-011-0866-z
Aber hab nur kurz draufgeschaut... |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 04. Nov 2014 13:56 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: | | Du nimmst doch an, dass jedes Teilchen in dem Schirm absorbiert wird. D.h. j ist hinter dem Schirm 0, somit kannst Du einen kleinen Kasten von epsilon-dicke um den Schirm legen, mit Seiten parallel zum Schirm, einmal davor einmal dahinter. |
OK, klar. Und was integrierst du über dieses Volumen? Oder die Oberfläche?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 04. Nov 2014 14:02 Titel: |
|
|
|
j uber die Oberfläche -> Satz von Gauss: div j über das Volumen -> Kontinuitätsgleichung: rho über das Volumen. |
|
|
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
| bassiks Verfasst am: 04. Nov 2014 14:41 Titel: |
|
|
Ich denke nicht dass das funktioniert, zumindest nicht mit der Argumentation dass für j für alle t, j(x>x_schirm,t)=0 gilt.
Damit ist j in x=x_schirm nicht für alle t stetig differenzierbar und der Satz von Gauß kann hier nicht angewendet werden.
Zur Lösung deines Problems TomS kann ich derzeit leider nichts vernünftiges Beitragen, hatte aber auch noch keine Zeit mir ernsthaft darüber Gedanken zu machen. Vllt. kommt noch was... |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 04. Nov 2014 16:07 Titel: |
|
|
ich denke auch nicht, dass das funktioniert, denn
1) wenn das Volumen V gem. dem o.g. Vorschlag gewählt wird, stellt der Schirm eine Senke für den Wahrscheinlichkeitsfluss dar, d.h. die Kontinuitätsgleichung gilt im Inneren von V nicht (Absorption)
2) der Gaußsche Integralsatz funktioniert nur, wenn eine geschlossene Oberfläche verwendet wird, dies hilft wg. (1) jedoch nicht weiter
ich denke, ich versuch's mal mit zeitabhängiger Streutheorie ...
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 04. Nov 2014 16:21 Titel: |
|
|
| TomS hat Folgendes geschrieben: | ich denke auch nicht, dass das funktioniert, denn
1) wenn das Volumen V gem. dem o.g. Vorschlag gewählt wird, stellt der Schirm eine Senke für den Wahrscheinlichkeitsfluss dar, d.h. die Kontinuitätsgleichung gilt im Inneren von V nicht (Absorption) |
Das ist doch auch so:
Wenn ich messe, kollabiert die Wellenfunktion, das Teilchen ist an einer einer Wahrscheinlichkeit rho^2 an dieser bestimmten Stelle des Schirms lokalisiert und nirgends anders.
Ich glaub ich hab noch nicht genau verstanden wieso Du überhaupt vom Wahrscheinlichkeitsfluss anfangen willst. Ich glaub was Du möchtest, ist eine vollständige Lösung der Schroedinger-Gleichung mit einem Potential, das den Doppelspalt beschreibt (unendliche Barriere mit Schlitzen) und dann vllt im unendlichen (am Anfang) von einer ebenen Welle beschrieben wird. Das hab ich noch nie gesehen, wäre aber interessant mal zu sehen  |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 04. Nov 2014 16:58 Titel: |
|
|
Nee, das will ich gar nicht ;-)
Nehmen wir an, ich habe eine stationäre Lösung der SGL; eben Welle vor der Blende; dann zwei punktförmige Löcher; dahinter zwei Kugelwellen; auf dem Schirm kann ich aus den Kugelwellen das Interferenzmuster berechnen. Gut!
Nehmen wir an, ich habe ein freies, zunächst eng lokalisiertes Wellenpaket vor der Blende; dann zwei punktförmige Löcher; dahinter eine komplizierte Welle gemäß der Zeitentwicklung mittels SGL; selbst wenn ich die SGL exakt lösen könnte, habe ich nur zeitabhängiges Wellenpaket, d.h. die Aufenthaltswahrscheinlichkeit auf dem Schirm ist nicht stationär; das erwartete Muster erhalte ich jedoch durch dier "Integration des Flusses" durch den Schirm über die Zeit"
D.h. selbst wenn ich die Lösung der SGL hinter dem Schirm exakt berechnen könnte, habe ich immer noch keine allgemeingültige Methode, um die Schwärzung einer Photoplatte (statt dces Schirmes) zu berechnen; die Wsk.-dichte ist es jedenfalls nicht!
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 04. Nov 2014 17:08 Titel: |
|
|
Wieso geht das nicht mit der W'keitsdichte^2? Du haelst z=0 fest (da ist der unendlich dünne Schirm) und Integrierst dann über kleine Umgebungen und eine Zeitspanne, vom Beginn des Auftreffens des Wellenpaketes bis zum End (in welcher Näherung auch immer). Das gibt Dir die W'keit in der Zeitspanne an der Stelle des Schirms ein Signal zu erhalten.
Das wäre meiner Meinung nach der natürlichere Weg dieses Problem zu behandeln... oder wie sieht Deine Born-Regel (welche ein Axiom ist) mithilfe des W'keitsflusses aus? |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 04. Nov 2014 17:22 Titel: |
|
|
also
} dV\,\rho)
ja, warum nicht? und warum nicht meine Idee mit dem Fluss?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 04. Nov 2014 17:35 Titel: |
|
|
Ich finde dies naheliegender, weil die Born-Regel etwas über die Verknüpfung von Messung und W'keitsdichte aussagt.
Vllt ist es möglich etwas analoges für den W'keitsfluss zu postulieren... ich erinnere mich allerdings nicht so etwas schonmal gesehen zu haben... wäre sicher interessant... |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 04. Nov 2014 17:40 Titel: |
|
|
ich habe beides noch nie gesehen, auch kein Zeitintegral über die Wsk.-dichte ...
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 04. Nov 2014 17:59 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | ich habe beides noch nie gesehen, auch kein Zeitintegral über die Wsk.-dichte ... |
Wir betrachten das Problem ja auch selten dynamisch, also als einzelne anfliegende zeitabhängige Wellenpakete, weil man das vermutlich eh schlecht (gar nicht?) beobachten kann. Ich glaub in der normalen Berechnung ist so eine implizite Integration schon enthalten ("alle Teilchen landen irgendwann auf dem Schirm"). |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 04. Nov 2014 22:53 Titel: |
|
|
So, hab' mal nachgedacht. Es geht einfach um die normale Definition des Streuquerschnitts, an die ich mich dunkel erinnert habe. Siehe Wikipedia - gekürzt:
the differential cross section is defined as follows: let a beam of intensity I_0 (measured in number of particles per area per time) be incident on a scattering center ... the number of scattered particles per solid angle per time [is] I_s ... we define the differential cross section to be
Mir geht es nun gar nicht um den Streuquerschnitt, sondern um ... the number of scattered particles per solid angle per time is I_s ... bzw. meine daraus resultierende Umformung ... the number of scattered particles is I_s integrated over solid angle and time ...
Das hatte ich noch irgendwo abgespeichert und daraus resultierte mein Ansatz, den Strom j über eine Fläche sowie die Zeit zu integrieren.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 05. Nov 2014 08:25 Titel: |
|
|
Hallo, bin ziemlich ratlos.
Ich kann mittels Kontinutitätsgleichung sowie Greenschen Formeln und Gaußschem Satz rumspielen. Letztere kann ich jedoch nur bei geschlossenen Flächen anwenden, und da habe ich keine Ahnung, wie ich diese sinnvoll legen soll. Bei offenen Flächen - und um eine solche handelt es sich - kann ich m.E. nicht weiter umformen.
Trotzdem bin ich aufgrund der Definition des Streuquerschnitts (Teilchenstrom pro Fläche und Zeit) der Meinung, dass der Ansatz eines Flächenintegrals über die Stromdichte der richtige Ansatz ist. Dann sollte man mittels einer geschickten Umformung oder Argumentation von der Stromdichte durch die Fläche zur Dichte selbst gelangen.
Ich suche also letztlich einen Weg, der folgendes liefert.
Gegeben sei ein (kleines) Flächenelement sowie ein zunächst eng lokalisiertes Wellenpaket, so dass psi in der Umgebung von S näherungsweise Null ist. Gegeben sei weiter die exakte Zeitentwicklung des Wellenpaketes (woher ich die habe ist irrelevant).
Ich behaupte, dass ich zunächst den Teilchen- bzw. Wahrscheinlichkeitsstrom j durch S benötige, um z.B. die Schwärzung einer Photoplatte bei S zu berechnen.
Ich suche einen Weg, wie ich vom Flächenintegral über j dS zu einem Ausdruck gelange, in dem statt j die Wahrscheinlichkeitsdichte rho (auf S oder in einem infinitesimalen Volumen mit dS als einer Begrenzung, also rho dV) gelange.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
| bassiks Verfasst am: 05. Nov 2014 09:58 Titel: |
|
|
Ich hab mir gestern nochmal Gedanken dazu gemacht.
Nachdem ich ebenfalls an einer Umformung gescheitert bin (Habe auch über Zeitableitungen etc. versucht die SG rein zubringen usw...), hab ich mir nochmal den Ansatz genauer angeschaut.
Auf den ersten Blick sieht er logisch und nachvollziehbar aus.
Folgende Überlegungen würde ich allerdings gerne einwerfen:
Die Modellierung über eine Fläche (2D!) mit 100% Absorption halte ich für problematisch. Wenn ich den Vergleich zur Hydrodynamik ziehe (was hier wohl durchaus plausibel erscheint), wäre das, als ob ich den Fluss durch eine nicht durchlässige Fläche betrachte. Dieser wäre immer 0. Der Schirm schafft also quasi gleiche Bedingungen wie ein unendlich hohes Potential. Ich denke der Ansatz funktioniert nur wenn man den Schirm mit endlicher Dicke betrachtet. Denn bei 100% Absorption am 2D Schirm habe ich das erwähnte Problem. Sobald ich dem Schirm ein Volumen zuspreche, kann ich das Umgehen. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 05. Nov 2014 10:40 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Ich suche einen Weg, wie ich vom Flächenintegral über j dS zu einem Ausdruck gelange, in dem statt j die Wahrscheinlichkeitsdichte rho (auf S oder in einem infinitesimalen Volumen mit dS als einer Begrenzung, also rho dV) gelange. |
Mit einem Volumen hast Du dann doch auch eine Oberfläche...
(modulo Vorzeichen, Integralgrenzen, etc..) |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 05. Nov 2014 12:47 Titel: |
|
|
| bassiks hat Folgendes geschrieben: | | Die Modellierung über eine Fläche (2D!) mit 100% Absorption halte ich für problematisch. |
Ich benötige nicht 100% Absorption; 100% Transmission ist OK; die Absorption kann auch (infinitesimal) hinter dem Schirm stattfinden
| bassiks hat Folgendes geschrieben: | | Der Schirm schafft also quasi gleiche Bedingungen wie ein unendlich hohes Potential. |
Das wäre jetzt 100% Reflexion und damit ganz verkehrt
Ich hatte schon darüber nachgedacht, hinter dem Schirm tatsächlich ein absobierendes Potential mit Imaginärteil anzunehmen. Ich sehe nur nicht unmittelbar, welche Schlussfolgerungen dann noch zulässig sind (bricht ein derartiges Potential die U(1)-Invarianz und damit das Noethertheorem / die Kontinuitätsgleichung?) Außerdem bin ich mir sicher, dass es auch ohne vernünftig gehen muss.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 05. Nov 2014 13:09 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: |
Ich suche einen Weg, wie ich vom Flächenintegral über j dS zu einem Ausdruck gelange, in dem statt j die Wahrscheinlichkeitsdichte rho (auf S oder in einem infinitesimalen Volumen mit dS als einer Begrenzung, also rho dV) gelange. |
Mit einem Volumen hast Du dann doch auch eine Oberfläche...
(modulo Vorzeichen, Integralgrenzen, etc..) |
Ja, soweit war ich auch schon.
Kernfrage: Wie legst du jetzt sinnvollerweise dein Volumen fest?
1) Wenn du ein infinitesimal dünnes Volumen annimmst, dann ist
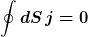
Der Strom fließt einfach durch das Volumen hindurch. Kann man sich anhand einer ebenen Welle und den Normalenvektoren n auch sofort klarmachen
 + \hat{n}_{z=\epsilon} \, j(\epsilon) = \hat{n} k + (-\hat{n}k) = 0)
Das passt auch zu
wenn V gegen 0.
2) Sinnvollerweise würdest du zunächst eine zweite Begrenzung für sehr großes z=L wählen, so dass das Wellenpaket nach sehr langer Zeit t=T praktisch vollständig im Gesamtvolumen enthalten ist. Also
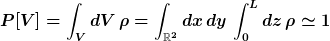
Soweit so gut.
3) Nun interessiert mich jedoch nicht der Fluss durch den gesamten Schirm, sondern durch eine kleine Fläche S auf dem Schirm. D.h. ich betrachte
Das Volumen ist dann sowas wie ein dünner Zylinder mit Bodenfläche S und extrem großer Länge L. Damit kann ich jedoch nicht arbeiten, den es ist ja
Der erste Term interessiert mich.
Der zweite Term liefert für große L sicher Null.
Den dritten Term, kann ich i.A. nicht vernachlässigen - es sei den, ich hätte eine ebene Welle in z-Richtung, den dann wären n und k orthogonal; letzteres darf ich aber i.A. nicht annehmen
Danke für die Bemühungen, aber ich sehe nicht, wie das funktionieren kann
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 05. Nov 2014 14:03 Titel: |
|
|
Wenn die W'keit das Teilchen in einem (beliebigen) Volumen zu messen, dann kann 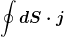 offensichtlich nicht Null sein.
Wenn ich das Volumen jetzt infinitesimal dünn mach, dann ist sowohl linke als auch rechte Seite Null, d.h. die Wahrscheinlichkeit ein Teilchen direkt]/i] in einer Ebene zu messen ist Null.. nicht weiter überraschend.. aber wieso sollte ich das ausrechnen wollen?*)
*) Wenn man jetzt sagt, dass rho da eine Delta-Distribution ist, dann stimmt das alles natürlich nicht mehr, inkl Deinem Argument.
Alles in Allem: Ich glaub, ich versteh immer noch nicht so ganz, wo Dein Problem liegt (oder [i]was Du dann eigentlich ausrechnen willst). |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 06. Nov 2014 22:48 Titel: |
|
|
Ich hab' nochmal nachgedacht. Es geht letztlich um folgendes: analysiert man z.B. das Doppelspaltexperiment mittels stationärer Lösungen, so hat es den Anschein, als ob das resultierende Interferenzmuster (bzw. die Häufigkeitsverteilung der detektierten Elektronen) durch die Wahrscheinlichkeitsdichte erklärt werden könnte.
Ich bin inzwischen der Meinung, dass das im Allgemeinen und insbs. für reale, nicht-stationäre Wellenpakete nicht zutrifft.
In diesem Fall muss man, übrigens genau wie für die Definition des differentiellen Streuquerschnitts, mit der Wahrscheinlichkeitsstromdichte argumentieren.
Gegeben sei also ein lokalisiertes Wellenpaket psi, ein Detektorschirm, sowie eine kleine Fläche S auf dem Detektorschirm. Modellieren wir die Teilchen durch ein Ensemble dieser Wellenpakete. Die Häufigkeitsverteilung auf dem Schirm folgt dann aus der Wahrscheinlichkeitsstromdichte; die Anzahl der in S detektierten Teilchen ist proportional zum Fluss durch S. Es verhält sich also so, wie in meinem ersten Beitrag beschrieben. Ich behaupte, dass in diesem Fall die Wahrscheinlichkeitsdichte nicht relevant ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 09. Nov 2014 15:48 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Ich bin inzwischen der Meinung, dass das im Allgemeinen und insbs. für reale, nicht-stationäre Wellenpakete nicht zutrifft.
|
Was trifft nicht zu? Dass das Experiment nicht erklärt werden kann?
| Zitat: |
In diesem Fall muss man, übrigens genau wie für die Definition des differentiellen Streuquerschnitts, mit der Wahrscheinlichkeitsstromdichte argumentieren.
|
Ich denke, ob man mit W'keitsdichte oder W'keitsstromdichte agiert ist egal. Letztendlich musst Du Deinen Formalismus irgendwie an eine Messung anbinden. Das geschieht normalerweise mit der Bornschen W'keitsinterpretation, welche die Dichte benutzt, aber ein umschreiben in die Stromdichte sollte nicht so schwer sein. (Ich denke dies ist der Punkt den Du in Deiner Betrachtung explizit vornehmen musst und wo die ganze Verwirrung herkommt.)
| Zitat: |
Die Häufigkeitsverteilung auf dem Schirm folgt dann aus der Wahrscheinlichkeitsstromdichte; die Anzahl der in S detektierten Teilchen ist proportional zum Fluss durch S. Es verhält sich also so, wie in meinem ersten Beitrag beschrieben. Ich behaupte, dass in diesem Fall die Wahrscheinlichkeitsdichte nicht relevant ist. |
Siehe oben: Was sagt meine Wellenfunktion über eine Messung aus?
PS: Im Peskin ist wird die Formel für den Wirkungsquerchnitt mit der W'keitsdichte und nicht der Stromdichte hergeleitet (Kapitel 4, insbesondere Eq. (4.74) und (4.75)). Aber um mich zu wiederholen: Beides geht und sollte äquivalent sein. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 09. Nov 2014 16:01 Titel: |
|
|
Natürlich kann das Experiment erklärt werden.
Du hast mein Problem nicht verstanden.
Im Falle eines nicht-stationären Wellenpakets funktioniert das zunächst nur mit der Wahrscheinlichkeitsstromdichte. Eine Argumentation mit der Wahrscheinlichkeitsdichte funktioniert nicht. Das gilt bereits für die Definition des Streuquerschnitts, wenn man ein Flächenelement auf dem Schirm mit den Raumwinkelelement identifiziert.
Ich hatte das oben schon geschrieben:
| TomS hat Folgendes geschrieben: | Es geht einfach um die normale Definition des Streuquerschnitts, an die ich mich dunkel erinnert habe. Siehe Wikipedia - gekürzt:
the differential cross section is defined as follows: let a beam of intensity I_0 (measured in number of particles per area per time) be incident on a scattering center ... the number of scattered particles per solid angle per time [is] I_s ... we define the differential cross section to be
Mir geht es nun gar nicht um den Streuquerschnitt, sondern um ... the number of scattered particles per solid angle per time is I_s ... bzw. meine daraus resultierende Umformung ... the number of scattered particles is I_s integrated over solid angle and time ... |
Das ist für mich die grundsätzlich gültige Überlegung.
Für den (eigtl. unrealistischen) Spezialfall einer stationäre Lösung argumentiert man mittels der Wahrscheinlichkeitsdichte und der Bornschen Regel.
Es gelingt mir aber nicht, eine Verbindung zwischen den beiden Argumentationen zu finden. Die naive Integration über die Zeit führt zu nichts.
Eine konkrete Frage an dich wäre folgende: Gegeben ist die o.g. Definition des Streuquerschnitts mittels der Wahrscheinlichkeitsstromdichte. Wie gelangt man von da auf eine Formulierung mittels Wahrscheinlichkeitsdichte? Und welche Voraussetzung müssen dafür erfüllt sein?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 09. Nov 2014 16:24 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Du hast mein Problem nicht verstanden.
|
Ich weiss 
| Zitat: |
Im Falle eines nicht-stationären Wellenpakets funktioniert das zunächst nur mit der Wahrscheinlichkeitsstromdichte. Das gilt bereits für die Definition des Streuquerschnitts, wenn man ein Flächenelement auf dem Schirm mit den Raumwinkelelement identifiziert.
|
Das seh ich nicht.
| Zitat: |
Ich hatte das oben schon geschrieben:
| TomS hat Folgendes geschrieben: | Es geht einfach um die normale Definition des Streuquerschnitts, an die ich mich dunkel erinnert habe. Siehe Wikipedia - gekürzt:
the differential cross section is defined as follows: let a beam of intensity I_0 (measured in number of particles per area per time) be incident on a scattering center ... the number of scattered particles per solid angle per time [is] I_s ... we define the differential cross section to be
Mir geht es nun gar nicht um den Streuquerschnitt, sondern um ... the number of scattered particles per solid angle per time is I_s ... bzw. meine daraus resultierende Umformung ... the number of scattered particles is I_s integrated over solid angle and time ... |
Das ist für mich die grundsätzlich gültige Überlegung.
|
Die Definition beinhaltet eine Teilchenstromdichte, keine W'keitsstromdichte... das ist für mich ein Unterschied und ich vermute es ist der entscheidende, da diese Auflösung zur Lösung hiervon führt:
| Zitat: |
Für den (eigtl. unrealistischen) Spezialfall einer stationäre Lösung argumentiert man mittels der Wahrscheinlichkeitsdichte und der Bornschen Regel. Es gelingt mir aber nicht, eine Verbindung zwischen den beiden Argumentationen zu finden. |
Meiner Meinung nach ist die Lösung das, was ich schonmal weiter oben geschrieben hatte. Ich versuch es nochmal:
Die Teilchenstromdichte in der Def aus Wiki, beinhaltet, dass dort ein Teilchen gemessen wird. D.h. ein Teilchen muss an einer Stelle des Schirm wechselwirken und diese Stellen sind (in einem realen Experiment) keine Flächen sondern kleine Volumina des Schirms. Und dann kann losgehen:
Born-Regel -> Kontinuitätsgleichung -> W'keitsstromdichte
Für (geeignete) zeitabhängige Wellenfunktionen, sollte dies dann in die übliche Lösung übergehen, wenn dann über alle Zeiten, in denen ein Teilchen messbar gewesen wäre, integriert wurde.
PS: Da ich mich im wesentlichen wiederholt hab, bist Du vermutlich der Meinung, dass ich Dich immer noch nicht verstanden hab |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 09. Nov 2014 16:37 Titel: |
|
|
Ja, du hast mich leider immer noch nicht verstanden.
Ich wiederhole nicht nochmal die Definition des Streuquerschnitts. Aber das Argument lautet wie folgt:
Die Häufigkeitsverteilung für detektierte Teilchen folgt aus dem Streuquerschnitt, dieser folgt aus der Wahrscheinlichkeitstromdichte. Also folgt die Schwärzung des Schirms beim Doppelspaltexperiment in der selben Weise (das Target ist einfach ein Doppelspalt).
Und natürlich entspricht die Wahrscheinlichkeitsstromdichte direkt der Teilchenstromdichte. So ist der Streuquerschnitt doch gerade definiert.
Ich stimme dir zu, dass die Wahrscheinlichkeitsdichte gemäß der Bornschen Regel eine Rolle spielen sollte, aber ich sehe diese Ableitung mathematisch nicht. Die Berechnung mittels der Stromdichte verstehe ich.
| jh8979 hat Folgendes geschrieben: | | Für (geeignete) zeitabhängige Wellenfunktionen, sollte dies dann in die übliche Lösung übergehen, wenn dann über alle Zeiten, in denen ein Teilchen messbar gewesen wäre, integriert wurde. |
Wäre schön, denn du sagen könntest, was die "übliche Lösung" ist, wie du integrierst, und was dein Ergebnis ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 09. Nov 2014 16:42 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Die Häufigkeitsverteilung für detektierte Teilchen folgt aus dem Streuquerschnitt, dieser folgt aus der Wahrscheinlichkeitstromdichte. Also folgt die Schwärzung des Schirms beim Doppelspaltexperiment in der selben Weise (das Target ist einfach ein Doppelspalt).
|
Dieser Schritt ist es den ich gern explizit sehen würde. Meiner Meinung nach ist es hier wo man ein Volumen im Schirm auswählen muss (oder falls nicht, sollte man sehen wieso nicht).
| Zitat: |
Und natürlich entspricht die Wahrscheinlichkeitsstromdichte direkt der Teilchenstromdichte. So ist der Streuquerschnitt doch gerade definiert.
|
Wenn ich die Teilchenstromdichte messe, dann muss ich doch ein Teilchen auf dem Schirm detektieren und der Schirm ist eben nicht unendlich dünn (und in dem Fall würde ich auch behaupten dass "keine Detektion" richtig wäre, da die W'keit mit einem unendlich dünnen Schien zu wechselwirken null ist). |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 09. Nov 2014 16:51 Titel: |
|
|
Siehe Kap. 7 im Sakurai
 \to e^{i\vec{k}\vec{x}} + \frac{e^{ikr}}{r}f(\vec{k},\vec{k}^\prime))
|^2\,d\Omega)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 09. Nov 2014 17:06 Titel: |
|
|
| Sakurai hat Folgendes geschrieben: |
We can then ask, what is the number of incident particles crossing a plane perpendicular to the indecent direction per unit area per unit time? This is just proportional to the probability flux [...]. Likewise we may ask, what is the number of scattered particles going into a small area  subtending a differential solid-angle element  ? Clearly, [...]
|
Wie wir wissen sind Aussagen, die auf "Clearly" folgen, immer alles andere als klar
Aber ernsthaft: Genau das meinte ich. Dort steht eine Behauptung, die so nicht ohne weiteres klar ist (naemlich die Verknüpfung zur W'keitsstromdichte). Die Worte klingen gut, aber das ist ja keine Begründung. Die Begründung ist meiner Meinung nach das, was ich schon weiter oben geschrieben hatte:
| jh8979 hat Folgendes geschrieben: |
..., d.h. "hinten" geht aus dem Schirm nichts raus, dort ist j=0 und du kannst Dein Integral über eine offene Flaeche in eins über eine geschlossene Fläche ändern, da die Beitrage verschwinden. Dann Satz von Gauss und man erhält den üblichen Ausdruck.
|

Das ist meiner Meinung nach die korrekte (=vollstaendige) Begründung für das was Sakurai geschrieben hat. Seine Definition des Wirkungsquerschnitts nimmt implizit an, dass auch alle Teilchen, welche in eine Richtung gestreut werden dort gemessen werden (= nichts geht durch den Schirm durch, d.h. j=0 hinter dem Schirm).
Ich bin damit ganz zufrieden, aber da Du vorher nicht zufrieden warst mit meiner Erklärung, bist Du es jetzt wohl auch (noch?) nicht
EDIT: Alternativ zu der "Nichts geht durch den Schirm"-Argumentation, kannst Du auch sagen, dass alle Teilchen die in einen Raumwinkel dOmega gehen irgendwie dort gemessen werden müssen. Man muss also die W'keitsdichte über das gesamte (unendliche) Volumen des dadurch definierten Raumes integrieren. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 09. Nov 2014 23:00 Titel: |
|
|
Ich stimme deiner Erklärung nicht zu.
Wie erreichst du, dass die Wahrscheinlichkeitsdichte hinter dem Schirm sehr schnell auf Null abfällt?
A) Reflexion am Schirm
B) Transmission durch den Schirm
C) Absorption in Schirm
A) ist unrealistisch. B) gilt es deiner Meinung nach gerade zu vermeiden. C) würde bedeuten, dass die Kontinuitätsgleichung nicht gilt.
Nochmal: betrachte ein Wellenpaket, das noch nahe des Schirms hinreichend gut lokalisiert ist und das auf diesen zuläuft. Was passiert deiner Meinung nach mit dem Wellenpaket?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 09. Nov 2014 23:04 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Wie erreichst du, dass die Wahrscheinlichkeitsdichte hinter dem Schirm sehr schnell auf Null abfällt?
|
Weil alle Teilchen, die in den Winkelbereich fliegen, am Schirm gemessen werden. Kontinuitätsgleichung gilt immer noch, die W'keitsdichte nimmt dann ja zu (das hab ich mir noch nicht so im Detail überlegt, aber glaub nicht dass es hier Probleme gibt.. und wenn sind es dieselben die beim "Kollaps der Wellenfunktion" immer auftreten).
Wenn Dir das nicht so gefällt, dann siehe mein EDIT oben: Alle Teilchen die irgendwie in den Winkelbereich fliegen, müssen (per Definition) irgendwo in diesem Winkelbereich detektiert werden...
Ich geb zu, dass ich hier nichts gerechnet hab und nur argumentiert, aber es würde mich schon ziemlich wundern, wenn diese Argumentation einer konkreten mathematischen Realisierung widersprechen würde. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18074
|
| TomS Verfasst am: 09. Nov 2014 23:21 Titel: |
|
|
| jh8979 hat Folgendes geschrieben: | | EDIT: Alternativ zu der "Nichts geht durch den Schirm"-Argumentation, kannst Du auch sagen, dass alle Teilchen die in einen Raumwinkel dOmega gehen irgendwie dort gemessen werden müssen. Man muss also die W'keitsdichte über das gesamte (unendliche) Volumen des dadurch definierten Raumes integrieren. |
Die Wsk.-Dichte zu welchem Zeitpunkt? Im Falle des Wellenpakets für alle Zeiten. D.h. also soetwas wie
wobei R_0 für die Entfernung eines kugelschalenförmigen Schirms steht.
Zeigst du mir, wie du von da zur normalen Definition des Streuquerschnitts kommst?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
Registrieren
Login
FAQ
Suchen
