| Autor |
Nachricht |
tusfo35
Anmeldungsdatum: 24.09.2014
Beiträge: 8
|
 tusfo35 Verfasst am: 24. Sep 2014 12:28 Titel: Integration Fourierreihe tusfo35 Verfasst am: 24. Sep 2014 12:28 Titel: Integration Fourierreihe |
 |
|
Meine Frage:
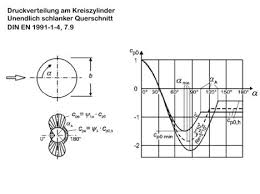
In Belastungsnormen werden Windruckverteilungen über den Umfang an Kreiszylinder mittels einer Fourierreihe dargestellt:
z.B.
 \varphi
<br />
)
mit

Die Druckbeiwerte stehen alle normal auf dem Kreisumfang. Ich möchte nun aus der Fourierreihe den resultierenden Druckbeiwert auf den Kreiszylinder ermitteln? Hat da jemand eine Idee?
Meine Ideen:
X
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7255
|
 Steffen Bühler Verfasst am: 24. Sep 2014 13:04 Titel: Steffen Bühler Verfasst am: 24. Sep 2014 13:04 Titel: |
 |
|
Willkommen im Physikerboard!
Der Ausdruck  \cdot \varphi) ist merkwürdig, das wäre ja der Cosinus des Laufindex n, multipliziert mit einem irgendeinem (was für einem?) Winkel. Der Ausdruck ist merkwürdig, das wäre ja der Cosinus des Laufindex n, multipliziert mit einem irgendeinem (was für einem?) Winkel. Der Ausdruck ) erscheint mir da plausibler. erscheint mir da plausibler.
Kann es daher sein, dass diese sechs Zahlen einfach den Druckvektor in Richtung von 0°, 60°, 120° und so weiter darstellen? Dann wäre das eine einfache Vektoraddition und hat nicht viel mit Fourier zu tun.
Viele Grüße
Steffen
|
|
 |
tusfo35
Anmeldungsdatum: 24.09.2014
Beiträge: 8
|
 tusfo35 Verfasst am: 25. Sep 2014 16:35 Titel: tusfo35 Verfasst am: 25. Sep 2014 16:35 Titel: |
 |
|
Danke für die Begrüßung und die Antwort!
Klingt alles plausibel. Klammer war verkehrt gesetzt! Ich habe die Vektoraddition mal durchgeführt. Für die X-Richtung (Definition quer zur Hauptwindrichtung) erhalte ich 0. Für die Y-Richtung (Hauptwindrichtung)erhalte ich als Resultierende 0,795. Kann das jemand bestätigen ?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7255
|
 Steffen Bühler Verfasst am: 25. Sep 2014 16:53 Titel: Steffen Bühler Verfasst am: 25. Sep 2014 16:53 Titel: |
 |
|
Wenn's so ist, wie ich vermute, würde mich die x-Komponente mit Null erstaunen. Wenn Du Dir die sechs Winkel aufmalst und die einzelnen Zahlenwerte dran, siehst Du, dass p2, also bei 120° mit 1,034 am größten ist. Die beiden benachbarten Komponenten sind auch positiv, während die gegenüberliegenden jeweils negativ sind, also auch noch in diese Richtung "drücken".
Somit sollte insgesamt schon mal ein negativer x-Wert herauskommen, denn der resultierende Zeiger liegt mit dieser Betrachtung jedenfalls im zweiten Quadranten.
Wenn ich die sechs Werte als komplexe Zahlen mit den jeweiligen Radien und den Winkeln 0°, 60° etc. addiere, erhalte ich folgerichtig auch -1,531+1,228i.
Oder verstehe ich was falsch?
Viele Grüße
Steffen
|
|
 |
tusfo35
Anmeldungsdatum: 24.09.2014
Beiträge: 8
|
 tusfo35 Verfasst am: 26. Sep 2014 08:21 Titel: tusfo35 Verfasst am: 26. Sep 2014 08:21 Titel: |
 |
|
|
Der Flankensog auf dem kompletten Zylinder müsste sich eigentlich aufheben, da er immer in entgegengesetzter Richtung wirkt, daher 0. Die Summe in Hauptwindrichtung ensteht durch Druck und Sog.
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7255
|
 Steffen Bühler Verfasst am: 26. Sep 2014 08:36 Titel: Steffen Bühler Verfasst am: 26. Sep 2014 08:36 Titel: |
 |
|
Davon verstehe ich leider nichts, vielleicht kann noch jemand anderes was dazu sagen.
Viele Grüße
Steffen
|
|
 |
jumi
Gast
|
 jumi Verfasst am: 26. Sep 2014 09:40 Titel: jumi Verfasst am: 26. Sep 2014 09:40 Titel: |
 |
|
tusfo,
könntest du mal vorrechnen, wie du auf die Resultierende = 0,795 kommst?
|
|
 |
tusfo35
Anmeldungsdatum: 24.09.2014
Beiträge: 8
|
 tusfo35 Verfasst am: 26. Sep 2014 10:30 Titel: tusfo35 Verfasst am: 26. Sep 2014 10:30 Titel: |
 |
|
Ich habe des Ergebnis für die Fouriereihe Z.B. bei einem Winkel von 0° = 0,95 in X-Richtung (0,95*sin0°) und in Y-Richtung (0,95*cos0°) zerlegt. Das hab ich in 3° Schritten bis 360° durchgeführt. Danach habe ich den jeweiligen Mittelwert der X-Y-Richtung mit einer anteilmäßigen Bogenlänge, bezogen auf die 3° Winkelunterschied, multipliziert und die Einzelwerte aufsummiert.
Ich habe aber noch ne andere Frage.
Folgende Fourierreihe ist gegeben:

aus der Literatur habe ich folgende Formel für eine Meridiankraft an einer Kreiszylinderschale:

z = Höhe Zylinder
a = Radius
Wie bringe ich die beiden Formel zusammen, damit ich die maximale Meridiankrfat bei z.B. einem Winkel von 180° erhalte?
|
|
 |
jumi
Gast
|
 jumi Verfasst am: 26. Sep 2014 13:00 Titel: jumi Verfasst am: 26. Sep 2014 13:00 Titel: |
 |
|
Was du da schreibst, ist wirres Zeug!
Kannst du denn nicht dein Problem verständlich beschreiben?
|
|
 |
tusfo35
Anmeldungsdatum: 24.09.2014
Beiträge: 8
|
 tusfo35 Verfasst am: 26. Sep 2014 13:25 Titel: tusfo35 Verfasst am: 26. Sep 2014 13:25 Titel: |
 |
|
Also nochmal langsam zum Mitdenken!
Für jeden Winkel alpha ergibt sich aus der gegebenen Fourierreihe ein Druckbeiwert der normal auf einer Kreisoberfläche steht/wirkt (siehe Anhang).
Soweit verständlich!
| Beschreibung: |
|
| Dateigröße: |
6.7 KB |
| Angeschaut: |
2144 mal |
|
|
|
 |
jumi
Gast
|
 jumi Verfasst am: 26. Sep 2014 14:00 Titel: jumi Verfasst am: 26. Sep 2014 14:00 Titel: |
 |
|
Aus dem Winkel phi wird plötzlich ein Winkel ß.
Weshalb soll man denn den Winkel von von 0 bis 360° betrachten?
Die Druckverteilung ist doch symmetrisch!
Ich gebe das Problem weiter an den nächsten Helfer.
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 26. Sep 2014 14:55 Titel: Huggy Verfasst am: 26. Sep 2014 14:55 Titel: |
 |
|
Das Diagramm lässt mich vermuten, dass es sich bei  doch um die ersten Glieder einer Fourierreihe handelt also: doch um die ersten Glieder einer Fourierreihe handelt also:
\approx \sum_{n=0}^5 p_n\cos(n\varphi))
Sei r der Radius des Zylinders und l seine Länge. Dann ergibt sich für die Kraft in x- bzw. y-Richtung:
\sin (\varphi)=0)
\cos (\varphi)=rl\int\limits_0^{2\pi}p_1\cos^2(\varphi)\approx 0.773\, rl)
Das passt einigermaßen zu deinem grob numerisch berechneten Wert.
Zu der Meridiankraft kann ich im Moment wenig sagen. Was ist mit Meridiankraft gemeint? Was genau ist z? Woher stammt die Formel?
Wenn man die Formel einfach mal als gegeben annimmt, brauchst du für 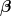 doch nur doch nur  einzusetzen. einzusetzen.
|
|
 |
tusfo35
Anmeldungsdatum: 24.09.2014
Beiträge: 8
|
 tusfo35 Verfasst am: 27. Sep 2014 07:30 Titel: tusfo35 Verfasst am: 27. Sep 2014 07:30 Titel: |
 |
|
Erst mal Danke für Deinen Beitrag!
Und danke für die analytische Betrachtung des Problems!!
Ich schreibe mal die ganze Aufgabe auf:
Eine am Fuß eingespannte vertikale Kreiszylinderschale (h = Höhe, r = Radius, t = Dicke der Schale) wird durch Wind belastet. Die Verteilung des Windes über den Umfang ist gegeben durch eine Fourierreihe der Form

mit

Berechnen Sie die maximale Meridiankraft im Einspannquerschnitt nach der Membrantheorie und vergleichen Sie diese mit der Lösung der Balkenbiegetheorie, wenn Sie in der Fourierreihe
a) nur die Glieder bis n=2 berücksichtigen
b) alle oben angegebenen Glieder berücksichtigen
Hilfsbeziehung:
² \, \dd \varphi =\frac{1}{2}\varphi +\frac{1}{4}sin2\varphi )
Lösungsansätze:
Höhe h wird weiterhin als l = Länge bezeichnet
Balkenbiegetheorie besagt S = M/W (S = Spannung, M = Moment, W = Widerstandsmoment)
mit M = 0,773 r l² / 2 (l / 2 als Hebelarm)
W = 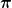 r² r²

Ich beziehe den Vergleich jetzt mal auf Spannungen:
Die Spannung aus der Balkenbiegetheorie soll jetzt mit einer Spannung die mittels Schalentheorie berechnet wurde verglichen werden.
Aus einem Buch Praktische Schalenstatik (Born) habe ich die Formel für die maximale Meridiankraft (Das ist die Kraft die in Längsrichtung des Zylinders wirkt) unter der gegebenen Winddruckverteilung mit

Die Spannung aus der Meridiankraft ist S = N / t.
Die maximale Meridiankraft muss bei 0° oder 180° liegen. Wie sieht denn die Formel für die Meridiankraft aus, wenn ich die Fourrierreihe einfüge?
Ist bei n² in der Formel die Größe der Anzahl an berücksichtigen Reihenglieder einzusetzen?
Im Voraus schon mal Vielen Dank!!
|
|
 |
jumi
Gast
|
 jumi Verfasst am: 27. Sep 2014 08:23 Titel: jumi Verfasst am: 27. Sep 2014 08:23 Titel: |
 |
|
|
Zitzerlweise kommt auch hier die Aufgabenstellung zum Vorschein!
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 27. Sep 2014 11:00 Titel: Huggy Verfasst am: 27. Sep 2014 11:00 Titel: |
 |
|
Mit der Schalentheorie war ich nie befasst. Da kann ich dir also nicht weiterhelfen. Die Formel für N sollte so zu verstehen sein:

Es ist für jeden Summanden der Summe für n der aktuelle Summationsindex einzusetzen. Dann ergibt sich aber das Maximum bei ca. 77.6 ° zu
 \approx 8,62 \frac{l²}{2r})
Bei 0 ° ergibt sich:
 \approx -6,48 \frac{l²}{2r})
Keine Ahnung, ob das so ein sinnvolles Ergebnis ist.
|
|
 |
tusfo35
Anmeldungsdatum: 24.09.2014
Beiträge: 8
|
 tusfo35 Verfasst am: 29. Sep 2014 07:48 Titel: tusfo35 Verfasst am: 29. Sep 2014 07:48 Titel: |
 |
|
|
Wie kommst Du z.B. bei 0° auf -6,48?
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 29. Sep 2014 08:32 Titel: Huggy Verfasst am: 29. Sep 2014 08:32 Titel: |
 |
|
Bei  hat man hat man
=\cos 0=1) . .
Dann lautet die Summe in der Formel für N nach meiner Interpretation bei  : :

|
|
 |
tusfo35
Anmeldungsdatum: 24.09.2014
Beiträge: 8
|
 tusfo35 Verfasst am: 29. Sep 2014 10:19 Titel: tusfo35 Verfasst am: 29. Sep 2014 10:19 Titel: |
 |
|
Ja Vielen, vielen Dank. Ich hatte 0² bei p0 nicht angesetzt. Es macht auch Sinn dass die maximale Kraft bei der Flankenbeanspruchung von 77,6° herauskommt. Ich hatte die ganze Zeit die resultierende Beanspruchung im Kopf, das ist aber bei der Schalenbetrachtung natürlich nicht richtig.
Gerade nochmal eine Frage zu der in meiner Aufgabenstellung angegebenen Hilfsbeziehung: Was könnte ich denn mit dieser anfangen?
|
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 29. Sep 2014 11:15 Titel: Huggy Verfasst am: 29. Sep 2014 11:15 Titel: |
 |
|
|
Das kann ich dir nicht sagen. Ich kann nur vermuten, dass zunächst eine allgemeine Formel für N in Form eines Integrals gegeben ist und dass man bei der weiteren Umformung bzw. Auswertung des Integrals die Hilfsbeziehung anwenden kann.
|
|
 |
|
















