| Autor |
Nachricht |
MartinMD95
Anmeldungsdatum: 23.10.2015
Beiträge: 4
|
|
 |
yellowfur
Moderator
Anmeldungsdatum: 30.11.2008
Beiträge: 804
|
 yellowfur Verfasst am: 23. Okt 2015 11:45 Titel: |
 |
|
Willkommen beim Physikerboard!
Das sieht doch schon sehr gut aus. Du kannst alle Teilströme abschnittsweise integrieren, wie du die Intervalle und Funktionen auch angegeben hast. Die gesamte Ladung ist dann die Summe aller Teilstücke unter Beachtung des Vorzeichens. Wenn die Aufgabe noch die Teilladungen wissen will, dann sind das die Lösungen deiner einzelnen Integrale, die du eh rechnen musst, bevor du aufsummierst.
_________________
Wenn du einen Traum hast, dann folge ihm. Wer weiß, wo er dich hinführen könnte. |
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
| ML Verfasst am: 23. Okt 2015 12:02 Titel: Re: Ladung durch Integration berechnen |
|
|
Hallo,
| MartinMD95 hat Folgendes geschrieben: |
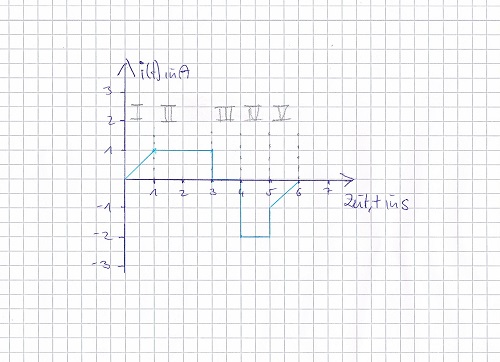
a) Ich habe das Diagramm in fünf Abschnitte unterteilt mit den jeweiligen Funktionsgleichungen.
I) i(0<=t<1s) =1A/s * t
II) i(1<=t<3s) =1A
III) i(3<=t<4s) =0
IV) i(4<=t<5s) =-2A
V) i(5<=t<6s) =1A/s *t-6A
|
bis auf die Schreibweise, die ein wenig ungewöhnlich ist, ist das soweit ok.
Ich würde die Bedingung für t nicht in die Klammer setzen. Im Beispiel I sähe das dann so aus:
 = 1\,\frac{\mathrm{A}}{\mathrm{s}} \cdot t;~~~~ 0 \le t < 1\,\mathrm{s})
Im Zweifel verwendest Du aber am besten die Schreibweise, die bei Euch üblich ist, damit keine Missverständnisse aufkommen.
| Zitat: |
Ich muss die erste Gleichung integrieren, was noch ganz gut klappt
 1 (A/s)*t \, \dd t )
=0,5 As.
|
Ja, es gibt aber ein paar Dinge zu beachten:
1) gehört f(t) nicht ins Integral rein. Du willst doch irgendwas mit i(t) schreiben. Das hast Du allerdings schon eingesetzt.
2) sollst Du q als Funktion von t angeben. Das bedeutet, dass in den Integralgrenzen ein t stehen muss und innerhalb des Integrals dieses t nicht auftauchen darf. Ich habe daher 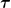 geschrieben. (Du hast gleich feste Grenzen eingesetzt -- das ist auch gefragt, aber nicht das wesentliche.)
3) musst Du die jeweils zum Anfangszeitpunkt schon geflossene Ladung mit einrechnen (was Deine eigentliche Frage beantworten sollte).
Die Antwort ist wiederum abschnittsweise:
=0)
 = q(0) + \int_0^t i(\tau) \cdot \mathrm{d}\tau =0 +\int_0^t \mathrm{\frac{1A}{s}} \cdot \tau \cdot \mathrm{d}\tau = \frac{1}{2} \mathrm{A} \cdot t; ~~~~~~~~~ 0 \le t < 1\,\mathrm{s})
= 0{,}5\,\mathrm{C})
 = q(1 \, \mathrm{s}) + \int_{\mathrm{1\,s}}^{t} i(\tau) \cdot \mathrm{d}\tau = ... ; ~~~~ 1\,\mathrm{s} \le t < 3\,\mathrm{s})
 = ... ) (durch Einsetzen in die vorherige Gl.)
...
Viele Grüße
Michael
|
|
|
MartinMD95
Anmeldungsdatum: 23.10.2015
Beiträge: 4
|
| MartinMD95 Verfasst am: 23. Okt 2015 12:22 Titel: |
|
|
Super, danke für die Nachrichten, das habe ich verstanden. 
Das mit dem f(t) im Integral war natürlich nicht richtig,
Also angenommen ich will für den zweiten Abschnitt jetzt die Ladung ausrechnen, so muss ich doch i(1<=t<3s) =1A integrieren.
Als Kontrolllösung habe ich aber
Q(t)= 1A*t-0,5As . Da frage ich mich, woher die -0,5 As herkommen. Denn ich soll doch eigentlich die Ladungen, die bisher geflossen sind, hinzuaddieren? Oder habe ich jetzt schlichtweg was falsch verstanden?
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
| ML Verfasst am: 23. Okt 2015 18:28 Titel: |
|
|
Hallo,
| MartinMD95 hat Folgendes geschrieben: |
Also angenommen ich will für den zweiten Abschnitt jetzt die Ladung ausrechnen, so muss ich doch i(1<=t<3s) =1A integrieren.
Als Kontrolllösung habe ich aber
Q(t)= 1A*t-0,5As . Da frage ich mich, woher die -0,5 As herkommen.
|
Der Ansatz steht ja oben schon da, jetzt musst Du nur noch einsetzen und rechnen. Spätestens, wenn Du die untere Integrationsgrenze in die Stammfunktion einsetzt, dürftest Du langsam ahnen, wo der Term -0,5 As herkommt. ;-)
 = q(1 \, \mathrm{s}) + \int_{\mathrm{1\,s}}^{t} i(\tau) \cdot \mathrm{d}\tau = 0{,}5\,\mathrm{C} + \int_{\mathrm{1\,s}}^{t} 1 \mathrm{A} \cdot \mathrm{d}\tau = 0{,}5\,\mathrm{C} + \left(1\, \mathrm{A} \cdot t - 1\, \mathrm{A} \cdot 1\,\mathrm{s}\right) = 1\, \mathrm{A} \cdot t - 0{,}5 \, \mathrm{As}; ~~~~ 1\,\mathrm{s} \le t < 3\,\mathrm{s})
Viele Grüße
Michael
|
|
|
MartinMD95
Anmeldungsdatum: 23.10.2015
Beiträge: 4
|
| MartinMD95 Verfasst am: 23. Okt 2015 18:58 Titel: |
|
|
Super, ich glaube jetzt habe ichs.
Als Beispiel für 4sek, also für den 4.Abschnitt wäre es dann:
=q(4s)+\int_4^t \! i(T) \, \dd T =2,5C+ \int_4^t \! -2A \, \dd T =2,5C+(-2A*t+2*4)=-2A*t+10,5C)
Wirklich super Hilfe hier, ich danke noch mal recht herzlich. Wäre bloß super, wenn das was ich da aufgeschrieben habe, auch richtig ist, wenn ja, habe ich es endlich verstanden.
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3388
|
| ML Verfasst am: 23. Okt 2015 22:48 Titel: |
|
|
Hallo,
| MartinMD95 hat Folgendes geschrieben: | Super, ich glaube jetzt habe ichs.
Als Beispiel für 4sek, also für den 4.Abschnitt wäre es dann:
Wirklich super Hilfe hier, ich danke noch mal recht herzlich. Wäre bloß super, wenn das was ich da aufgeschrieben habe, auch richtig ist, wenn ja, habe ich es endlich verstanden. |
ja, sieht soweit vernünftig aus. Du müsstest aber die Grenzen mit Einheiten eingeben (d. h. "4 s" statt "4"), sonst geht das Ganze formal gesehen nicht auf, und Du bekommst Abzüge bei der Klausur.
Viele Grüße
Michael
|
|
|
Anon12213
Gast
|
| Anon12213 Verfasst am: 02. Aug 2017 13:31 Titel: |
|
|
Und wie sieht das dann beim letzten Abschnitt aus?
Also bei 5 < t < 6
Bleib da irgendwie hängen..
|
|
|
Anon12213
Gast
|
| Anon12213 Verfasst am: 02. Aug 2017 14:48 Titel: |
|
|
Wenn ichs verstanden hab, was ich eigtl dachte, müsste es ja ca. so ablaufen:
q(t)=q(5s)+\int_5^t \! i(T) \, \dd T=0,5As+\left[\frac{1}{2}\frac{A}{s}*T^2-6A*T\right]_{5}^{t}=\frac{1}{2}\frac{A}{s}*t^2-6A*t-42As
Mein Bauchgefühl sagt mir aber, dass das nicht richtig ist so.. Kann mir jemand den Fehler aufzeigen?[/latex]
|
|
|
Anon12213
Gast
|
| Anon12213 Verfasst am: 02. Aug 2017 14:49 Titel: |
|
|
| Anon12213 hat Folgendes geschrieben: | Wenn ichs verstanden hab, was ich eigtl dachte, müsste es ja ca. so ablaufen:
q(t)=q(5s)+\int_5^t \! i(T) \, \dd T=0,5As+\left[\frac{1}{2}\frac{A}{s}*T^2-6A*T\right]_{5}^{t}=\frac{1}{2}\frac{A}{s}*t^2-6A*t-42As
Mein Bauchgefühl sagt mir aber, dass das nicht richtig ist so.. Kann mir jemand den Fehler aufzeigen?[/latex] |
=q(5s)+\int_5^t \! i(T) \, \dd T=0,5As+\left[\frac{1}{2}\frac{A}{s}*T^2-6A*T\right]_{5}^{t}=\frac{1}{2}\frac{A}{s}*t^2-6A*t-42As)
- Sorry!
|
|
|
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7241
|
| Steffen Bühler Verfasst am: 02. Aug 2017 15:36 Titel: |
|
|
Bis auf den letzten Schritt passt es. Für t musst Du natürlich 6s einsetzen und die 42As beim Einsetzen von 5s stimmen nicht, wohl ein kleiner Rechenfehler.
Viele Grüße
Steffen
|
|
|
Anon12213
Gast
|
| Anon12213 Verfasst am: 03. Aug 2017 07:29 Titel: |
|
|
Wenn ich aber doch für t 6s einsetze krieg ich keine Funktion für q in Abhängikeit von t, die ich ja will?
Und den Fehler beim einsetzen von t=5s find ich leider nicht.:
Der vorherige Abschnitt wird ja so beschrieben:
=-2A*t+10,5As)
Also ist =0,5As)
Und wenn das hier stimmt sehen die einzelnen Rechenschritte ja derart aus:
^2-6A*5s=
<br />
0,5As+\frac{1}{2} \frac{A}{s} *t^2-6A*t-12,5As-30As=
<br />
0,5As+\frac{1}{2} \frac{A}{s} *t^2-6A*t-42,5As=
<br />
\frac{1}{2} \frac{A}{s} *t^2-6A*t-42As)
Und wo genau mach ich jetzt den Rechenfehler?:/ 
|
|
|
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7241
|
| Steffen Bühler Verfasst am: 03. Aug 2017 11:54 Titel: |
|
|
Du willst - genau wie bei den anderen Berechnungen - nur die Ladung berechnen, die in dem Zeitintervall dazugekommen ist. Und das ist nun mal das bestimmte Integral, hier mit den Grenzen 5s und 6s.
Dein kleiner Rechenfehler ist, dass Du in der ersten Zeile nicht geklammert hast. Dadurch ist der Term 6A*5s negativ geworden, er muss aber positiv sein.
|
|
|
Physikamateur
Anmeldungsdatum: 21.10.2018
Beiträge: 16
|
| Physikamateur Verfasst am: 22. Dez 2018 21:14 Titel: |
|
|
Ich bearbeite momentan paar Beispielaufgaben zur Prüfungsvorbereitung. Leider sehe ich das Endergebnis nicht, daher meine Lösung:
ist das Endergebnis = -13 As?
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 23. Dez 2018 02:13 Titel: |
|
|
| Physikamateur hat Folgendes geschrieben: | | ist das Endergebnis = -13 As? |
Nein. Die Gesamtladung ist die Fläche unter der i(t)-Funktion. Da siehst Du - auch ohne Rechnung - sofort, dass Dein Ergebnis nicht stimmen kann.
Wie groß ist die Fläche oberhalb und wie groß die Fläche unterhalb der t-Achse? Wenn Du diese Flächen vorzeichenrichtig addierst, erhältst Du das richtige Ergebnis.
|
|
|
|
Registrieren
Login
FAQ
Suchen
