| Autor |
Nachricht |
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
 J_spgs Verfasst am: 08. Dez 2020 10:05 Titel: Seillänge einer Hebekonstruktion berechnen |
 |
|
Guten Tag
Ich bin momentan verzwiefelt daran eine scheinbar einfache Aufgabe lösen zu wollen, komme aber nicht auf den richtigen Pfad.
Aufgabe: Ich muss für ein Transportband eine Hebekonstruktion konstruieren.
Gegeben sind die beiden Längen A und B(siehe Bild) und der Winkel 33° mit welchem das Band eingebaut werden muss. Die Verbindung C wird eine Kettenverbindung und für das Heben des Gewichtes zuständig sein. Da der Befestigungspunkt aber hinter dem Schwerpunkt ist muss ich noch einen Gegendruck A haben damit das Transportband nicht nach unten kippt. A ist somit eine feste Verbindung und der Befestigungs punkt ist drehbar. Somit ist der Winkel "Transportband zu Verbindung A" nicht gegeben. Ich muss jetzt herausfinden wie lange die Verbindung C sein muss damit sich die 33° ergeben. Um das herauszufinden muss ich wissen wie sich die Baugruppe auspendelt. Das Gewicht des Transportbandes ist 50Kg.
Herausmessen ist leider nicht möglich weil ich für die Verbindung C nicht viel Spielraum in der Maschine habe(siehe Bild 2).
Ich hoffe die Aufgabe ist einigermassen verständlich damit ihr euch den Kopf darüber zerbrechen könnt;)
Vielen Dank für eure Hilfe!
| Beschreibung: |
| Die Situation mit allen Angaben |
|
Download |
| Dateiname: |
01_Berechnung Transportband.pdf |
| Dateigröße: |
78.48 KB |
| Heruntergeladen: |
378 mal |
| Beschreibung: |
|
Download |
| Dateiname: |
02_Situation in der Maschine.pdf |
| Dateigröße: |
1.5 MB |
| Heruntergeladen: |
309 mal |
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5923
Wohnort: jwd
|
| Mathefix Verfasst am: 08. Dez 2020 11:12 Titel: |
|
|
Frage: Soll A senkrecht auf B stehen?
Ansonstens ist das System unterbestimmt - Es gibt unendlich viele Lösungen.
Schlage einen Kreisbogen um den Schnittpinkt A/B mit dem Radius A. Dann siehst Du, dass es für C bliebig viele Längen gibt, die den Kreisgogen schneiden.
Es fehlt ein Winkel oder eine Längenangabe z.Bsp. Position des Kranhakens.
|
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5972
|
| Myon Verfasst am: 08. Dez 2020 11:42 Titel: |
|
|
Es fehlt die Angabe, in welchem Abstand sich der Schwerpunkt des Transportbands vom Aufhängepunkt der Kette befindet. Allenfalls wäre das Gewicht der Kette noch relevant, falls dieses nicht vernachlässigbar ist gegenüber dem Gewicht des Transportbands.
Das Ganze pendelt sich natürlich so ein, dass der Schwerpunkt senkrecht unter dem Haken liegt.
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5923
Wohnort: jwd
|
| Mathefix Verfasst am: 08. Dez 2020 12:42 Titel: |
|
|
| Myon hat Folgendes geschrieben: |
...
Das Ganze pendelt sich natürlich so ein, dass der Schwerpunkt senkrecht unter dem Haken liegt. |
IN REVISION Schwerpunkt kann Ausserhalb von B liegen
Genau so. Damit ist die Position des Kranhakens bestimmt.
Wenn die Lage des Schwerpunkts auf B bekannt ist, lässt sich C bestimmen:
s_1 = Abstand des Schwerpunkts von B von der Anlenkung B
s_2 = Abstand Schwerpunkt vom Aufhängepunkt der Kette
Alpha = Gegebener Winkel von 33°
Gamma = Winkel h/s_2 = 90 + Alpha = 123° (Dreieck h/s_2/C)
h = Vertikaler Abstand Kranhaken/Schwerpunkt
 }+ s_1 \cdot \sin(\alpha ))
 } )
Zuletzt bearbeitet von Mathefix am 08. Dez 2020 13:01, insgesamt einmal bearbeitet |
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 08. Dez 2020 12:59 Titel: |
|
|
| Myon hat Folgendes geschrieben: | Es fehlt die Angabe, in welchem Abstand sich der Schwerpunkt des Transportbands vom Aufhängepunkt der Kette befindet. Allenfalls wäre das Gewicht der Kette noch relevant, falls dieses nicht vernachlässigbar ist gegenüber dem Gewicht des Transportbands.
Das Ganze pendelt sich natürlich so ein, dass der Schwerpunkt senkrecht unter dem Haken liegt. |
Diese Angabe habe ich vergessen zu teilen.
Die Kräfte an beiden Enden kenne ich bereits. Hier mal meine Berechnungen.
| Beschreibung: |
|
Download |
| Dateiname: |
Berechnung Schwerpunkt Transportband.pdf |
| Dateigröße: |
66.55 KB |
| Heruntergeladen: |
294 mal |
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5923
Wohnort: jwd
|
| Mathefix Verfasst am: 08. Dez 2020 13:09 Titel: |
|
|
| J_spgs hat Folgendes geschrieben: | | Myon hat Folgendes geschrieben: | Es fehlt die Angabe, in welchem Abstand sich der Schwerpunkt des Transportbands vom Aufhängepunkt der Kette befindet. Allenfalls wäre das Gewicht der Kette noch relevant, falls dieses nicht vernachlässigbar ist gegenüber dem Gewicht des Transportbands.
Das Ganze pendelt sich natürlich so ein, dass der Schwerpunkt senkrecht unter dem Haken liegt. |
Diese Angabe habe ich vergessen zu teilen.
Die Kräfte an beiden Enden kenne ich bereits. Hier mal meine Berechnungen. |
Welchen Abstand hat der Schwerpunkt von der Anlenkung B bzw. von dem Aufhängpunkt von C?
|
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 08. Dez 2020 13:23 Titel: |
|
|
| Mathefix hat Folgendes geschrieben: | Frage: Soll A senkrecht auf B stehen?
Ansonstens ist das System unterbestimmt - Es gibt unendlich viele Lösungen.
Schlage einen Kreisbogen um den Schnittpinkt A/B mit dem Radius A. Dann siehst Du, dass es für C bliebig viele Längen gibt, die den Kreisgogen schneiden.
Es fehlt ein Winkel oder eine Längenangabe z.Bsp. Position des Kranhakens. |
Ich könnte A senkrecht zu B stellen. Dann würden aber mehr Kräfte auf die Befestigung A-B wirken was ich lieber vermeiden würde.
Wie wäre die Idee mit einem grossen Kräftedreieck. Wenn man die Kräfte die auf Punkt A-B und Punkt B-C wirken kennen würde, könnte man mit der Formel F1xl1=F2x(L-l1) den Schwerpunkt des Transportbandes zwischen den beiden Befestigungspunkten berechnen.
|
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 08. Dez 2020 13:25 Titel: |
|
|
| Mathefix hat Folgendes geschrieben: | | J_spgs hat Folgendes geschrieben: | | Myon hat Folgendes geschrieben: | Es fehlt die Angabe, in welchem Abstand sich der Schwerpunkt des Transportbands vom Aufhängepunkt der Kette befindet. Allenfalls wäre das Gewicht der Kette noch relevant, falls dieses nicht vernachlässigbar ist gegenüber dem Gewicht des Transportbands.
Das Ganze pendelt sich natürlich so ein, dass der Schwerpunkt senkrecht unter dem Haken liegt. |
Diese Angabe habe ich vergessen zu teilen.
Die Kräfte an beiden Enden kenne ich bereits. Hier mal meine Berechnungen. |
Welchen Abstand hat der Schwerpunkt von der Anlenkung B bzw. von dem Aufhängpunkt von C? |
Vom Aufhängepunkt A-B bis zum Schwerpunkt sind es 1300mm.
Vom Aufhängepunkt B-C bis zum Schwerpunkt sind es 563mm
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5923
Wohnort: jwd
|
| Mathefix Verfasst am: 08. Dez 2020 14:01 Titel: |
|
|
| J_spgs hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | | J_spgs hat Folgendes geschrieben: | | Myon hat Folgendes geschrieben: | Es fehlt die Angabe, in welchem Abstand sich der Schwerpunkt des Transportbands vom Aufhängepunkt der Kette befindet. Allenfalls wäre das Gewicht der Kette noch relevant, falls dieses nicht vernachlässigbar ist gegenüber dem Gewicht des Transportbands.
Das Ganze pendelt sich natürlich so ein, dass der Schwerpunkt senkrecht unter dem Haken liegt. |
Diese Angabe habe ich vergessen zu teilen.
Die Kräfte an beiden Enden kenne ich bereits. Hier mal meine Berechnungen. |
Welchen Abstand hat der Schwerpunkt von der Anlenkung B bzw. von dem Aufhängpunkt von C? |
Vom Aufhängepunkt A-B bis zum Schwerpunkt sind es 1300mm.
Vom Aufhängepunkt B-C bis zum Schwerpunkt sind es 563mm |
Bei dem gegebenen Winkel und der Länge A liegt der Schwerpunkt nicht senkrecht unter dem Haken, da A< 1.300mm ist.
|
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5923
Wohnort: jwd
|
| Mathefix Verfasst am: 10. Dez 2020 12:26 Titel: |
|
|
| J_spgs hat Folgendes geschrieben: |
Vom Aufhängepunkt A-B bis zum Schwerpunkt sind es 1300mm.
Vom Aufhängepunkt B-C bis zum Schwerpunkt sind es 563mm |
Ist die anhängende Skizze korrekt?
| Beschreibung: |
|
Download |
| Dateiname: |
Krankette.pdf |
| Dateigröße: |
43.35 KB |
| Heruntergeladen: |
320 mal |
|
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 10. Dez 2020 13:39 Titel: |
|
|
| Mathefix hat Folgendes geschrieben: | | J_spgs hat Folgendes geschrieben: |
Vom Aufhängepunkt A-B bis zum Schwerpunkt sind es 1300mm.
Vom Aufhängepunkt B-C bis zum Schwerpunkt sind es 563mm |
Ist die anhängende Skizze korrekt? |
Ja die erste Skizze ist korrekt.
Ich versuche mit der festen Verbindung einen gegendruck zu erzeugen damit die Konstruktion auch im Gleichgewicht bei 33° zur horizontalen hängt. Deine zweite Skizzen würde stimmen wenn beide Verbindungen zuerst zusammenführen und dann an den Haken gehängt wird.
Wenn man aber beide einzeln dranhängt sollte sich das ganze mit 33° auspendeln. Ich versuche jetzt mit einem Kräfte-dreieck den Schwerpunkt zu errechnen.
|
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 10. Dez 2020 13:42 Titel: |
|
|
| Nils Hoppenstedt hat Folgendes geschrieben: | Hallo,
mit folgendem Vorgehen solltest du die Aufgabe lösen können.
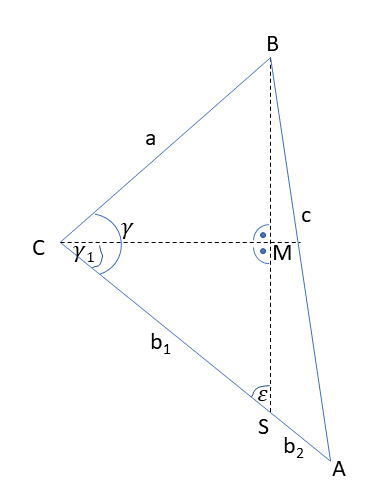
Gegeben: a, b1, b2, 
Gesucht: c
Man berechnet:
1. Im Dreeick CSM den Winkel 
2. Im Dreieck BCS den Winkel  (Ssw)
3. Im Dreieck ABC schließlich die Seite c (sws)
Hierbei beziehen sich die Ausdrücke Ssw und sws auf die bekannten Formeln zur Dreicksberechnung.
(siehe z.B. hier: https://www.arndt-bruenner.de/mathe/scripts/Dreiecksberechnung.htm )
Viele Grüße,
Nils |
Hallo Nils
Genau deine Lösung scheint mir logisch.
Meine Frage ist nur von wo man b1 und b2 hat weil der Schwerpunkt ausserhalb vom Dreieck ist. Oder geht dein Dreieck vom einen Ende des Tranportband zum anderen?
|
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
| Nils Hoppenstedt Verfasst am: 10. Dez 2020 13:57 Titel: |
|
|
| J_spgs hat Folgendes geschrieben: |
Genau deine Lösung scheint mir logisch.
Meine Frage ist nur von wo man b1 und b2 hat weil der Schwerpunkt ausserhalb vom Dreieck ist. Oder geht dein Dreieck vom einen Ende des Tranportband zum anderen? |
Sorry, ich habe die Diskussion leider nicht komplett gelesen und bin davon ausgegangen, dass der Schwerpunkt zwischen den Aufhängepunkten liegt.
Viele Grüße,
Nils
|
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 10. Dez 2020 14:28 Titel: |
|
|
| Nils Hoppenstedt hat Folgendes geschrieben: | | J_spgs hat Folgendes geschrieben: |
Genau deine Lösung scheint mir logisch.
Meine Frage ist nur von wo man b1 und b2 hat weil der Schwerpunkt ausserhalb vom Dreieck ist. Oder geht dein Dreieck vom einen Ende des Tranportband zum anderen? |
Sorry, ich habe die Diskussion leider nicht komplett gelesen und bin davon ausgegangen, dass der Schwerpunkt zwischen den Aufhängepunkten liegt.
Viele Grüße,
Nils |
Kein problem
Aber danke für deine Bemühungen:)
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5923
Wohnort: jwd
|
| Mathefix Verfasst am: 10. Dez 2020 17:36 Titel: |
|
|
| Nils Hoppenstedt hat Folgendes geschrieben: | | J_spgs hat Folgendes geschrieben: |
Genau deine Lösung scheint mir logisch.
Meine Frage ist nur von wo man b1 und b2 hat weil der Schwerpunkt ausserhalb vom Dreieck ist. Oder geht dein Dreieck vom einen Ende des Tranportband zum anderen? |
Sorry, ich habe die Diskussion leider nicht komplett gelesen und bin davon ausgegangen, dass der Schwerpunkt zwischen den Aufhängepunkten liegt.
Viele Grüße,
Nils |
Hallo Nils
Ist mir anfangs auch passiert, da nicht bekannt war, wo der Schwerpunkt liegt.
Knobele gerade an der Lösung anhand meiner Skizze.
Gruss
mathefix
|
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
| Nils Hoppenstedt Verfasst am: 10. Dez 2020 18:01 Titel: |
|
|
Hallo Mathefix,
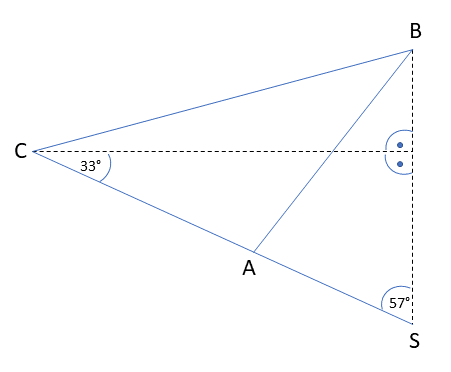
Ich hab die Aufgabe so verstanden, dass der Winkel zur Horizontalen 33° sein soll. Da der Schwerpunkt S sich natürlich senkrecht unter dem Haken befinden muss, sieht das Ganze also so aus wie in der Skizze unten.
Wenn der Abstand AS = 1300 mm ist, folgt aus diesen Angaben, dass die gestrichelte horizontale Linie in der Skizze ca. 1090 mm lang ist. Dann muss die steife Befestigung BC aber auch größer sein als 1090 mm. Laut Aufgabenstellung ist sie aber nur 780 mm lang.
Also entweder habe ich die Aufgabe nicht richtig verstanden oder das kann so nicht funktionieren.
Viele Grüße,
Nils
| Beschreibung: |
|
| Dateigröße: |
8.89 KB |
| Angeschaut: |
40002 mal |
|
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5923
Wohnort: jwd
|
| Mathefix Verfasst am: 10. Dez 2020 18:16 Titel: |
|
|
| Nils Hoppenstedt hat Folgendes geschrieben: | Hallo Mathefix,
Ich hab die Aufgabe so verstanden, dass der Winkel zur Horizontalen 33° sein soll. Da der Schwerpunkt S sich natürlich senkrecht unter dem Haken befinden muss, sieht das Ganze also so aus wie in der Skizze unten.
Wenn der Abstand AS = 1300 mm ist, folgt aus diesen Angaben, dass die gestrichelte horizontale Linie in der Skizze ca. 1090 mm lang ist. Dann muss die steife Befestigung BC aber auch größer sein als 1090 mm. Laut Aufgabenstellung ist sie aber nur 780 mm lang.
Also entweder habe ich die Aufgabe nicht richtig verstanden oder das kann so nicht funktionieren.
Viele Grüße,
Nils |
Hallo Nils,
Du hast recht;darüber war ich auch gestolpert (Bei dem gegebenen Winkel und der Länge A liegt der Schwerpunkt nicht senkrecht unter dem Haken, da A< 1.300mm ist). Meine Annahme ist, dass der Winkel zur Horizontale im nicht angehobenenen Zustand 33° beträgt. Wenn das Teil angehoben wird, dann kippt es in die Gleichgewichtslage und die Horizontale kippt mit (s. meine Skizzen) d.h. der Winkel zwischen Den Seiten A und B bleibt konstant. Der Aufgabensteller hat auf meine Frage, ob die Skizzen korrekt seien, bisher nicht geantwortet. Deshalb macht es m.E. im Augenblick keinen Sinn weiterzumachen.
Gruss
mathefix
PS
Da der Winkel zwischen A und B fix ist, dann sind SWS gegeben und C kann mit dem Cosinusatz bestimmt werden. Der Fragesteller muss nur diesen konstruktiv vorgegebenen Winkel nennen. Der Winkel soll nach seiner Aussage aus Lastgründen nicht 90° sein. Ohne Angabe des Winkels existieren für C beliebig viele Lösungen.
Zuletzt bearbeitet von Mathefix am 10. Dez 2020 18:29, insgesamt einmal bearbeitet |
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
| Nils Hoppenstedt Verfasst am: 10. Dez 2020 18:28 Titel: |
|
|
| Mathefix hat Folgendes geschrieben: | | Du hast recht;darüber war ich auch gestolpert (Bei dem gegebenen Winkel und der Länge A liegt der Schwerpunkt nicht senkrecht unter dem Haken, da A< 1.300mm ist). |
Ach stimmt, auf diesen Widerspruch bist du ja auch schon gestoßen. Ich sollte echt die anderen Beiträge aufmerksamer lesen, Asche auf mein Haupt.
Und ja, du hast Recht, solange der Widerspruch nicht geklärt ist, macht es keinen Sinn hier weiterzumachen.
Viele Grüße,
Nils
|
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 11. Dez 2020 08:12 Titel: |
|
|
| J_spgs hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | | J_spgs hat Folgendes geschrieben: |
Vom Aufhängepunkt A-B bis zum Schwerpunkt sind es 1300mm.
Vom Aufhängepunkt B-C bis zum Schwerpunkt sind es 563mm |
Ist die anhängende Skizze korrekt? |
Ja die erste Skizze ist korrekt.
Ich versuche mit der festen Verbindung einen gegendruck zu erzeugen damit die Konstruktion auch im Gleichgewicht bei 33° zur horizontalen hängt. Deine zweite Skizzen würde stimmen wenn beide Verbindungen zuerst zusammenführen und dann an den Haken gehängt wird.
Wenn man aber beide einzeln dranhängt sollte sich das ganze mit 33° auspendeln. Ich versuche jetzt mit einem Kräfte-dreieck den Schwerpunkt zu errechnen. |
Hallo Mathefix
Ich habe in diesem Beitrag auf deine Frage geantwortet.
Ich entschuldige mich für das durcheinander
|
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 11. Dez 2020 08:23 Titel: |
|
|
| Nils Hoppenstedt hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | | Du hast recht;darüber war ich auch gestolpert (Bei dem gegebenen Winkel und der Länge A liegt der Schwerpunkt nicht senkrecht unter dem Haken, da A< 1.300mm ist). |
Ach stimmt, auf diesen Widerspruch bist du ja auch schon gestoßen. Ich sollte echt die anderen Beiträge aufmerksamer lesen, Asche auf mein Haupt.
Und ja, du hast Recht, solange der Widerspruch nicht geklärt ist, macht es keinen Sinn hier weiterzumachen.
Viele Grüße,
Nils |
Stellt es euch so vor. Ich habe unten mal ein Bild von einem Bleistift angehängt.
gegeben:
S= Schwerpunkt
A/B= Befestigungspunkt
Stellen wir uns vor wir halten den Bleistift an Punkt A fest. Der Bleistift wird sich am Punkt A nach unten drehen weil er vor dem Schwerpunkt ist und so kein Gleichgewicht herrscht
Wenn wir jetzt aber gleichzeitig wenn wir Punkt A halten, mit dem Finger auf Punkt B draufdrücken, sind wir in der Lage den Bleistift in eine beliebige Position in einem beliebigen Winkel einzustellen. Das ist genau das Prinzip welches ich bei meinem Transportband anwende.
Eure Lösung würde aber genauso stimmen, wenn beide Verbindungen zusammengeführt werden und dann am Haken befestigt werden. Wenn aber einmal die Verbindung C als Halterung und einmal die Verbindung A als Gegendruck am Haken einzeln befestigt wird, sollte meiner Meinung nach die Konstruktion nicht mehr nacht unten kippen und sich nicht über dem Schwerpunkt einpendeln.
Ich hoffe das hat euch ein wenig geholfen.
Mathefix
Weiter oben habe ich auf deine Skizzen geantwortet
| Beschreibung: |
|
Download |
| Dateiname: |
Beispiel Gleichgewicht.pdf |
| Dateigröße: |
21.79 KB |
| Heruntergeladen: |
284 mal |
|
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
| Nils Hoppenstedt Verfasst am: 11. Dez 2020 09:42 Titel: |
|
|
Danke für die Erläuterungen. Ich denke, vom Prinzip her war uns beiden schon klar, wie du dir das vorstellst, aber es gab noch ein paar Unklarheiten bezüglich der Zahlenwerte. Also konkret: Ist mit dem Winkel von 33° der Winkel des Förderbands (Strecke CS in meiner letzten Skizze) gegenüber der Horizontalen im angehobenen Zustand gemeint?
Viele Grüße,
Nils
|
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 11. Dez 2020 09:52 Titel: |
|
|
| Nils Hoppenstedt hat Folgendes geschrieben: | Danke für die Erläuterungen. Ich denke, vom Prinzip her war uns beiden schon klar, wie du dir das vorstellst, aber es gab noch ein paar Unklarheiten bezüglich der Zahlenwerte. Also konkret: Ist mit dem Winkel von 33° der Winkel des Förderbands (Strecke CS in meiner letzten Skizze) gegenüber der Horizontalen im angehobenen Zustand gemeint?
Viele Grüße,
Nils |
Ja genau
Das Förderband muss 33° zur horizontalen in die Maschine eingebaut werden. Ich kenne die Masse der Festen Verbindung die ich selbst konstruiert habe, den Abstand zum Schwerpunkt und die Position der Befestigung der Verbindung C. Der Schwerpunkt wird mit sicherheit nicht Senkrecht unter dem Haken sein.
Zuletzt bearbeitet von J_spgs am 11. Dez 2020 10:00, insgesamt einmal bearbeitet |
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
| Nils Hoppenstedt Verfasst am: 11. Dez 2020 09:59 Titel: |
|
|
| J_spgs hat Folgendes geschrieben: | | Das Förderband muss 33° zur horizontalen in die Maschine eingebaut werden. |
Wie gesagt: Dann komme ich zu dem Schluss, dass das Ganze wegen der Randbedingung, dass der Schwerpunkt sich immer unterhalb der Aufhängung befindet nicht funktioniert (siehe mein Posting vom 10. Dez 2020 18:01).
- Nils
|
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 11. Dez 2020 10:05 Titel: |
|
|
| Nils Hoppenstedt hat Folgendes geschrieben: | | J_spgs hat Folgendes geschrieben: | | Das Förderband muss 33° zur horizontalen in die Maschine eingebaut werden. |
Wie gesagt: Dann komme ich zu dem Schluss, dass das Ganze wegen der Randbedingung, dass der Schwerpunkt sich immer unterhalb der Aufhängung befindet nicht funktioniert (siehe mein Posting vom 10. Dez 2020 18:01).
- Nils |
Hallo Nils
Meinst du die Berechnung funktioniert nicht oder die Halterung?
|
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
| Nils Hoppenstedt Verfasst am: 11. Dez 2020 10:20 Titel: |
|
|
Lass es mich so ausdrücken: Die Annahme, dass sich jeder beliebige Winkel einstellen lässt, ist nicht richtig. Die Länge der festen Verbindung beschränkt den minimal möglichen Winkel zur Horizontalen bzw. für einen vorgegebenen Winkel ergibt sich eine Mindestlänge für die feste Verbindung. Im vorliegenden Fall muss die feste Verbindung mindestens 1090 mm lang sein.
- Nils
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5923
Wohnort: jwd
|
| Mathefix Verfasst am: 11. Dez 2020 10:23 Titel: |
|
|
Ich klinke mich mal ein.
Ich entnehme Deiner Konstruktion, dass die Verbindung AB fest ist und AC sowie BC mit Kranhaken gelenkig. Ist das so?
Wenn ja, wird sich die Konstruktion nach dem Anheben so einpendeln, dass sich der Schwerpunkt senkrecht unter dem Aufhängepunkt von AC am Kranhaken befindet - s. meine Skizze.
Wenn Du B in der vorgegebenen Lage gehalten werden soll, muss C während des Anhebevorgangs gekürzt werden.
Zuletzt bearbeitet von Mathefix am 11. Dez 2020 10:38, insgesamt einmal bearbeitet |
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 11. Dez 2020 10:36 Titel: |
|
|
| Mathefix hat Folgendes geschrieben: | Ich klinke mich mal ein.
Ich entnehme Deiner Konstruktion, dass die Verbindung AB fest ist und AC sowie BC mit Kranhaken gelenkig. Ist das so?
Wenn ja, wird sich die Konstruktion nach dem Anheben so einpendeln, dass sich der Schwerpunkt senkrecht unter dem Aufhängepunkt von AC am Kranhaken befindet - s. meine Skizze. |
Also diese Annahme kann ich leider nicht teilen. Ich habe mal einen kleinen Prototyp gemacht der genauso funktioniert. Zwei Verbindungen die einzeln an einem Haken befestigt sind und das ganze hat super funktioniert. Ich konnte dann je nach seillänge den Winkel einstellen.
|
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 11. Dez 2020 10:40 Titel: |
|
|
-Kein Text-
Zuletzt bearbeitet von J_spgs am 11. Dez 2020 10:44, insgesamt einmal bearbeitet |
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 11. Dez 2020 10:43 Titel: |
|
|
[quote="Nils Hoppenstedt"]Lass es mich so ausdrücken: Die Annahme, dass sich jeder beliebige Winkel einstellen lässt, ist nicht richtig. Die Länge der festen Verbindung beschränkt den minimal möglichen Winkel zur Horizontalen bzw. für einen vorgegebenen Winkel ergibt sich eine Mindestlänge für die feste Verbindung. Im vorliegenden Fall muss die feste Verbindung mindestens 1090 mm lang sein.
- Nils[/quote
Diese Annahme macht sinn. Dh. ich müsste die Feste Verbindung mindestens 1090mm lang machen damit die 33° überhaupt möglich sind?
Kommt das nicht eher auf das Verhältnis Lose Verbindung zu feste Verbindung an oder liege ich da falsch?
|
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
| Nils Hoppenstedt Verfasst am: 11. Dez 2020 10:43 Titel: |
|
|
|
Entscheidend sind die Abmessungen, insbesondere die Lage des Schwerpunkts. Wenn diese Maße bei deinem Prototypen nicht identisch sind mit denen im späteren Bauteil kannst du das Ergebnis nicht übertragen.
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5923
Wohnort: jwd
|
| Mathefix Verfasst am: 11. Dez 2020 10:43 Titel: |
|
|
| J_spgs hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | Ich klinke mich mal ein.
Ich entnehme Deiner Konstruktion, dass die Verbindung AB fest ist und AC sowie BC mit Kranhaken gelenkig. Ist das so?
Wenn ja, wird sich die Konstruktion nach dem Anheben so einpendeln, dass sich der Schwerpunkt senkrecht unter dem Aufhängepunkt von AC am Kranhaken befindet - s. meine Skizze. |
Also diese Annahme kann ich leider nicht teilen. Ich habe mal einen kleinen Prototyp gemacht der genauso funktioniert. Zwei Verbindungen die einzeln an einem Haken befestigt sind und das ganze hat super funktioniert. Ich konnte dann je nach seillänge den Winkel einstellen. |
Wenn die Verbindung AB fest ist und damit der Wnkel A/B konstant, existiert nur eine Länge von C - ergibt sich aus dem Cosinussatz.
|
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
| Nils Hoppenstedt Verfasst am: 11. Dez 2020 10:49 Titel: |
|
|
| J_spgs hat Folgendes geschrieben: |
Dh. ich müsste die Feste Verbindung mindestens 1090mm lang machen damit die 33° überhaupt möglich sind?
|
Ja. (wobei es aus mechanischer Sicht vorteilhafter ist, wenn es noch ein bisschen länger wäre).
| J_spgs hat Folgendes geschrieben: |
Kommt das nicht eher auf das Verhältnis Lose Verbindung zu feste Verbindung an oder liege ich da falsch? |
Nein, das Verhältnis alleine ist nicht hinreichend.
Viele Grüße,
Nils
|
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 11. Dez 2020 10:50 Titel: |
|
|
|
Nur zur richtigstellung. Fest bedeutet nicht das die Verbindung nicht im Winkel einstellbar ist, sondern nur das sie auch gegendruck leisten kann. Also der Winkel würde sich von selbst einstellen.
|
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 11. Dez 2020 10:51 Titel: |
|
|
ich denke ich muss das ganze nochmals richtig überdenken.
Ich informiere euch dann wenn ich mehr weiss.
Vielleicht habt ihr ja einen besseren Lösungsvorschlag
Vielen Dank für eure Hilfe schon im Voraus:)
|
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
| Nils Hoppenstedt Verfasst am: 11. Dez 2020 11:06 Titel: |
|
|
| J_spgs hat Folgendes geschrieben: | | Nur zur richtigstellung. Fest bedeutet nicht das die Verbindung nicht im Winkel einstellbar ist, sondern nur das sie auch gegendruck leisten kann. Also der Winkel würde sich von selbst einstellen. |
Ja, so habe ich das auch verstanden.
|
|
|
VeryApe
Anmeldungsdatum: 10.02.2008
Beiträge: 3273
|
| VeryApe Verfasst am: 11. Dez 2020 11:09 Titel: |
|
|
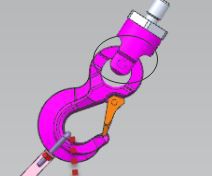
Der Haken ist doch trotzdem dort drehbar, wo die schwarze Ellipse ist oder nicht?
Dann würde sich doch das ganze mit Haken drehen, daß der Gesamtschwerpunkt genau unterhalb liegt.
| Beschreibung: |
|
| Dateigröße: |
15.3 KB |
| Angeschaut: |
39829 mal |
|
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5923
Wohnort: jwd
|
| Mathefix Verfasst am: 11. Dez 2020 11:15 Titel: |
|
|
| J_spgs hat Folgendes geschrieben: | | Nur zur richtigstellung. Fest bedeutet nicht das die Verbindung nicht im Winkel einstellbar ist, sondern nur das sie auch gegendruck leisten kann. Also der Winkel würde sich von selbst einstellen. |
Wenn die Verbindung AB gelenkig = linksdrehbar von 33° bis 180° ist, dann liegt der geometrische Ort AC auf dem Kreis mit dem Mittelpunkt AB und dem Radius A.
|
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 11. Dez 2020 11:17 Titel: |
|
|
| VeryApe hat Folgendes geschrieben: | Der Haken ist doch trotzdem dort drehbar, wo die schwarze Ellipse ist oder nicht?
Dann würde sich doch das ganze mit Haken drehen, daß der Gesamtschwerpunkt genau unterhalb liegt. |
Mein Fehler. Wir haben in meiner Firma keine Modelle des originalen Hakens. Unser Haken hat kein Gelenk in sich. Das ist nur ein Beispielmodell
|
|
|
J_spgs
Anmeldungsdatum: 08.12.2020
Beiträge: 27
Wohnort: St.Gallen
|
| J_spgs Verfasst am: 11. Dez 2020 11:20 Titel: |
|
|
| Mathefix hat Folgendes geschrieben: | | J_spgs hat Folgendes geschrieben: | | Nur zur richtigstellung. Fest bedeutet nicht das die Verbindung nicht im Winkel einstellbar ist, sondern nur das sie auch gegendruck leisten kann. Also der Winkel würde sich von selbst einstellen. |
Wenn die Verbindung AB gelenkig = linksdrehbar von 33° bis 180° ist, dann liegt der geometrische Ort AC auf dem Kreis mit dem Mittelpunkt AB und dem Radius A. |
Ja genau
|
|
|
|
Registrieren
Login
FAQ
Suchen
