| Autor |
Nachricht |
The_Nati
Anmeldungsdatum: 29.10.2012
Beiträge: 34
|
 The_Nati Verfasst am: 28. Jun 2013 17:36 Titel: Eigenfunktion harmonischer Oszillator The_Nati Verfasst am: 28. Jun 2013 17:36 Titel: Eigenfunktion harmonischer Oszillator |
 |
|
Ich sitze grad bei der Prüfungsvorbereitung und hab bei dieser Aufgabe, die eigentlich realtiv einfach sein sollte, Probleme...
ich soll zeigen, dass die Funktion:
= \alpha \left ( 2 \frac{x^2}{l^2}-1 e^{-\frac 12 \frac{x^2}{l^2}}\right ) )
Eine Eigenfunktion des Harmonischen Oszillators ist.
Dazu nutzt man den Hamilton operator in Orstdarstellung:

So also erstmal die Ableitungen bilden:
 =\alpha \left ( \frac{4x}{l^2}+\left (\frac{2x^2}{l^2}\right ) \left (\frac{-1}{2}\frac{2x}{l^2}\right ) +\frac{x}{l^2} \right ) e^{-\frac{1}{2} \frac{x^2}{l^2}} = \alpha \left ( \frac{5x}{l^2}-\frac{2x^3}{l^4}\right ) e^{-\frac 12 \frac{x^2}{l^2}} )
Zweite Ableitung:
=\alpha \left [ \frac{ 5}{l^2}-\frac{6x^2}{l^4}+\left (\frac{5x}{l^2}-\frac{2x^3}{l^4}\right ) \left ( -\frac{x}{l^2}\right )\right ]e^{\frac{-1}{2}\frac{x^2}{l^2}}= \alpha \left [ \frac{5}{l^2}-\frac{11x^2}{l^4}+\frac{2x^4}{l^4} \right]e^{\frac{-1}{2}\frac{x^2}{l^2}} )
l ist definiert als 
Somit ergibt sich :
 =\alpha \left [-\frac{5 \omega}{2}+\frac{11x^2}{2} \omega^2 m- m \omega^2 x^4 + \frac{m}{2}\omega^2 x^2 \right ]e^{\frac{-1}{2}\frac{x^2}{l^2}}=\alpha \left [ -\frac{5 \omega}{2}+\frac{12x^2}{2} \omega^2 m- m \omega^2 x^4 \right ] e^{\frac{-1}{2}\frac{x^2}{l^2}})
So eigentlich sollte die Funktion aber eine Eigenfunktion zu dem eigenwert 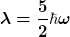 sein... sein...
Nur irgendwie klappt das nicht 
 |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 28. Jun 2013 22:52 Titel: jh8979 Verfasst am: 28. Jun 2013 22:52 Titel: |
 |
|
|
Dein Hamiltonoperator hat doch noch einen zweiten Term. Die Rechnung wird übrigens sehr viel übersichtlicher, wenn man statt x mit y=x/l rechnet. |
|
 |
The_Nati
Anmeldungsdatum: 29.10.2012
Beiträge: 34
|
 The_Nati Verfasst am: 29. Jun 2013 16:48 Titel: The_Nati Verfasst am: 29. Jun 2013 16:48 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | | Dein Hamiltonoperator hat doch noch einen zweiten Term. Die Rechnung wird übrigens sehr viel übersichtlicher, wenn man statt x mit y=x/l rechnet. |
Richtig. 
hab da ein bisschen was verschusselt...
hab's jetzt noch mal nachgerechnet und es passt 
eine Frage hätte ich aber noch...
Ersetzung hab ich jetzt zwar nicht ausprobiert aber macht schon Sinn das es dann einfcher wird 
Vielen Danke |
|
 |
Äther

Anmeldungsdatum: 22.12.2011
Beiträge: 387
|
 Äther Verfasst am: 29. Jun 2013 21:14 Titel: Äther Verfasst am: 29. Jun 2013 21:14 Titel: |
 |
|
| The_Nati hat Folgendes geschrieben: | | eine Frage hätte ich aber noch... |
Die wäre? |
|
 |
Robertus
Anmeldungsdatum: 13.06.2013
Beiträge: 12
|
 Robertus Verfasst am: 30. Jun 2013 17:55 Titel: Robertus Verfasst am: 30. Jun 2013 17:55 Titel: |
 |
|
Ich bearbeite die gleiche Aufgabe und komme beim besten Willen nicht auf die Lösung, obwohl ich die Ableitungen absolut korrekt habe (sogar mit Mathematica überprüft). Was danach bleibt ist ja prinzipiell nur umstellen und Terme kürzen, aber beim besten Willen. Ich komme niemals auf  . .
Die SGL lautet:

Die 2. Ableitung ist: 
Ich habe also folgende Gleichung:
)
Sinn und Zweck ist ja jetzt lediglich den Term ) auszuklammern, der Faktor wäre dann der Eigenwert. Dann habe ich also: auszuklammern, der Faktor wäre dann der Eigenwert. Dann habe ich also:
[\frac{1}{2} m \omega^2 x^2 + \frac{-\hbar^2}{2m}(\frac{-11x^2}{l^4} + \frac{5}{l^2} + \frac{2x^4}{l^6}) / (2\frac{x^2}{l^2} - 1)])
Das was in eckigen Klammern steht müsste sich jetzt also eigentlich zu meinem gesuchten Eigenwert zusammenkürzen. Tut es aber nicht. Selbst mit Mathematica nicht. Ich sehe da aber absolut nichts Falsches.
Nati, wie sieht das denn bei dir aus? Siehst du hier irgendwo einen Fehler bei mir?  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 30. Jun 2013 18:25 Titel: jh8979 Verfasst am: 30. Jun 2013 18:25 Titel: |
 |
|
Klammer nur  aus, dann siehst Du schnell dass das Polynom das übrig bleibt genau das ist was Du möchtest. aus, dann siehst Du schnell dass das Polynom das übrig bleibt genau das ist was Du möchtest. |
|
 |
Robertus
Anmeldungsdatum: 13.06.2013
Beiträge: 12
|
 Robertus Verfasst am: 30. Jun 2013 19:22 Titel: Robertus Verfasst am: 30. Jun 2013 19:22 Titel: |
 |
|
Ändert sich für mich nicht so viel:
 \frac{2}{m \omega^2} + x^2 \alpha e^{\frac{-x^2}{2l^2}}(2\frac{x^2}{l^2} - 1)])
Immer noch unübersichtlich wie Sau.  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 30. Jun 2013 19:52 Titel: jh8979 Verfasst am: 30. Jun 2013 19:52 Titel: |
 |
|
|
im zweiten Teil ist ein alpha und eine e-Funktion zuviel. Im ersten ein 1/l^2 aus klammern und Definition von l benutzen... Dann steht's schon so gut wie da: die beiden x^4 Terme heben sich weg und aus der -11 wird eine -10. |
|
 |
Robertus
Anmeldungsdatum: 13.06.2013
Beiträge: 12
|
 Robertus Verfasst am: 30. Jun 2013 21:42 Titel: Robertus Verfasst am: 30. Jun 2013 21:42 Titel: |
 |
|
Keine Chance, ich krieg's nicht aufgelöst. Kann machen was ich will, da kürzt sich nichts Sinnvolles weg. Hab's jetzt sicher 20 mal aufgeschrieben. Kannst ja gerne die Schritte aufschreiben, wenn du möchtest, ansonsten gebe ich die Aufgabe auf. Das nervt mich jetzt nämlich auch so langsam aber sicher.
Die 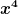 -Terme kürzen sich bei mir z. B. schon deshalb nicht weg, weil ich sowas stehen habe: -Terme kürzen sich bei mir z. B. schon deshalb nicht weg, weil ich sowas stehen habe:

Zur Übersicht nochmal:
 |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 30. Jun 2013 22:06 Titel: jh8979 Verfasst am: 30. Jun 2013 22:06 Titel: |
 |
|
 \frac{2}{m \omega^2} + x^2 (2\frac{x^2}{l^2} - 1) \right] )
Ist
 + x^2 (2\frac{x^2}{l^2} - 1) \right] )
Das ist
 + \frac{x^2}{l^2} (2\frac{x^2}{l^2} - 1) \right] )
und das ist

Und fertig:

.... solche Umformungen sollten sitzen...
Zuletzt bearbeitet von jh8979 am 30. Jun 2013 22:14, insgesamt einmal bearbeitet |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 30. Jun 2013 22:12 Titel: jh8979 Verfasst am: 30. Jun 2013 22:12 Titel: |
 |
|
Es waere allerdings viel einfacher gewesen von vorneherein y=x/l zu benutzen. Dann ist
 = \alpha \left[2 y^2 - 1 \right]e^{-\frac{y^2}{2}})
und
 . . |
|
 |
Robertus
Anmeldungsdatum: 13.06.2013
Beiträge: 12
|
 Robertus Verfasst am: 01. Jul 2013 03:51 Titel: Robertus Verfasst am: 01. Jul 2013 03:51 Titel: |
 |
|
Man, das ganze Problem an der Aufgabe war, dass auf dem Zettel angegeben ist:

Obwohl es eigentlich sein müsste:

Ist ja super nervig. Ich zweifle schon die ganze Zeit, ob ich keine stinknormalen Terme mehr umformen kann.
Danke nochmal für deine Mühe, jh8979. |
|
 |
|



















