| Potential unendlich ausgedehnter Linienladung |
| Autor | Nachricht | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| kommando_pimperlepim Anmeldungsdatum: 15.11.2004 Beiträge: 133 |
|
|||||||||||||||||
| dermarkus Administrator Anmeldungsdatum: 12.01.2006 Beiträge: 14788 |
|
|||||||||||||||||
| schnudl Moderator Anmeldungsdatum: 15.11.2005 Beiträge: 6979 Wohnort: Wien |
|
|||||||||||||||||
| kommando_pimperlepim Anmeldungsdatum: 15.11.2004 Beiträge: 133 |
|
|||||||||||||||||
| dermarkus Administrator Anmeldungsdatum: 12.01.2006 Beiträge: 14788 |
|
|||||||||||||||||
| schnudl Moderator Anmeldungsdatum: 15.11.2005 Beiträge: 6979 Wohnort: Wien |
|
|||||||||||||||||
| schnudl Moderator Anmeldungsdatum: 15.11.2005 Beiträge: 6979 Wohnort: Wien |
|
|||||||||||||||||
| Verwandte Themen - die Neuesten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Elektrisches Potential | 1 | Andrei | 85 | 24. Apr 2024 21:04 ML |
 |
Potential einer Kugelschale mit Poisson-Gleichung | 7 | Gast | 999 | 05. Feb 2024 14:43 jh8979 |
 |
Unendlich tiefer Potenzialtopf | 1 | Gast | 689 | 25. Jan 2024 13:30 willyengland |
 |
Energielücke am Brillouinzonenrand im periodischen Potential | 0 | TryingToUnderstandIt | 1094 | 18. Jan 2024 17:53 TryingToUnderstandIt |
 |
Potential eines Teilchen Umkehrpunkte | 8 | Sirius02 | 1934 | 11. Jan 2024 13:16 Myon |
| Verwandte Themen - die Größten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Universum endlich oder unendlich? | 105 | Erster Admiral | 10351 | 15. Dez 2021 19:40 TomS |
 |
Metallkugeln - Ladung - Potential - Feldstärke | 71 | Wilfried | 37491 | 29. Sep 2006 18:04 Wilfried |
 |
Teilchen im Potenzialtopf mit unendlich hohen Wänden | 53 | aaabbb | 11693 | 23. Feb 2017 11:01 TomS |
 |
Potential aus Kraft berechnen? | 40 | Physik_Student | 2424 | 27. Aug 2021 20:06 Physik_Student |
 |
Potential einer Linienladung | 39 | ohneplan123 | 12324 | 20. Jan 2015 16:45 ohneplan123 |
| Verwandte Themen - die Beliebtesten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Metallkugeln - Ladung - Potential - Feldstärke | 71 | Wilfried | 37491 | 29. Sep 2006 18:04 Wilfried |
 |
Elektrisches Potenzial einer Kugel | 7 | munich | 32770 | 26. Jan 2013 19:13 twb8t5 |
 |
Durch Magneten unendlich elektrische Energie gewinnen | 16 | Gerd | 30408 | 01. Jun 2018 20:23 [email protected] |
 |
Satz v Gauss,unendlich langer Zylinder | 14 | razer | 27111 | 01. Nov 2007 21:02 razer |
 |
unendlich langer Draht | 8 | eisley | 21844 | 22. Okt 2012 16:09 eisley |

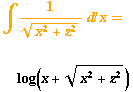
 In der bisherigen Rechnung war der Nullpunkt des Potentials nicht bei z=0, sondern "bei z=unendlich" gewählt, also so, dass das Potential im Unendlichen verschwand. (Und das machte in der Rechnung Probleme, denn dann werden mit dem Abstand z und der Leiterlänge gleich zwei Größen unendlich.)
In der bisherigen Rechnung war der Nullpunkt des Potentials nicht bei z=0, sondern "bei z=unendlich" gewählt, also so, dass das Potential im Unendlichen verschwand. (Und das machte in der Rechnung Probleme, denn dann werden mit dem Abstand z und der Leiterlänge gleich zwei Größen unendlich.)