| Autor |
Nachricht |
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
 Erster Admiral Verfasst am: 22. Aug 2021 13:15 Titel: Universum endlich oder unendlich? |
 |
|
Was genau ist denn der neueste Stand zur Endlichkeit bzw. Unendlichkeit des Universums?
Ich weiß:
1. Nach dem Kosmologischen Prinzip ist das Universum homogen und isotrop.
2. Messungen am CMB haben ergeben, dass das Universum auf kosmologischer Ebene eine euklidische Geometrie aufweist.
Aus beiden Aussagen zusammen folgere ich, dass die Materie unendlich weit in diesem euklidischen Raum verteilt sein muss.
Entspricht das auch dem momentanen Kenntnisstand in der Kosmologie?
Ich freu mich über alle Antworten und Literaturempfehlungen.
Zuletzt bearbeitet von Erster Admiral am 22. Aug 2021 15:48, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 22. Aug 2021 16:16 Titel: Re: Universum endlich oder unendlich? |
|
|
| Erster Admiral hat Folgendes geschrieben: | Was genau ist denn der neueste Stand zur Endlichkeit bzw. Unendlichkeit des Universums?
Ich weiß:
1. Nach dem Kosmologischen Prinzip ist das Universum homogen und isotrop.
2. Messungen am CMB haben ergeben, dass das Universum auf kosmologischer Ebene eine euklidische Geometrie aufweist.
Aus beiden Aussagen zusammen folgere ich, dass die Materie unendlich weit in diesem euklidischen Raum verteilt sein muss.
Entspricht das auch dem momentanen Kenntnisstand in der Kosmologie? |
Eine flache Raumzeit lässt auch kompakte = endliche Universen zu. Z.B. existiert für einen 3-Torus eine flache Geometrie (auch wenn man sich dies nicht gut vorstellen kann).
Für sehr kleinräumige Kompaktifizierungen könnte man dies astronomisch nachweisen, z.B. über Mehrfachbilder einer Galaxie oder auch über das Winkelspektrum der Hintergrundstrahlung (vergleiche das Schwingungsspektrum eines eingespannten Membran). Gegenwärtig gibt es m.W.n. dafür keine Anzeichen, d.h. das Universum ist entweder euklidisch und unendlich, oder zwar kompakt jedoch zu groß, um dies feststellen zu können.
Jede Kompaktifizierung verletzt die Isotropie "im Großen". Das kann man sich anhand von Kurven auf einem 2-Torus vorstellen. Geschlossene Kurven winden sich (m,n)-fach um den 2-Torus, bis sie wieder in sich selbst zurücklaufen; dabei sind m und n natürliche Zahlen, die sogenannten Windungszahlen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Günther
Anmeldungsdatum: 23.11.2010
Beiträge: 305
|
| Günther Verfasst am: 22. Aug 2021 18:32 Titel: |
|
|
Mit den Planck Daten ist das Universum fast flach. Die Messungenauigkeit liegt bei 0,4%. Das unterstützt zwar die Annahme euklidischer Geometrie, läßt aber auch eine hinreichend große 3-Sphäre zu.
Es ist aus heutiger Sicht wenig wahrscheinlich, dass diese Frage definitiv geklärt werden kann.
|
|
|
Aruna
Anmeldungsdatum: 28.07.2021
Beiträge: 795
|
| Aruna Verfasst am: 22. Aug 2021 20:16 Titel: Re: Universum endlich oder unendlich? |
|
|
| TomS hat Folgendes geschrieben: | d.h. das Universum ist entweder euklidisch und unendlich, oder zwar kompakt jedoch zu groß, um dies feststellen zu können.
|
Gibt es für ein euklidisches und unendliches Universum das sich ausdehnt eine Veranschaulichung?
|
|
|
Erster Admiral
Anmeldungsdatum: 07.05.2021
Beiträge: 69
|
| Erster Admiral Verfasst am: 22. Aug 2021 21:44 Titel: |
|
|
Worin genau würde sich denn der Torus mathematisch vom unendlichen euklidischen Raum unterscheiden?
Bzw. anhand welcher Eigenschaft kann man die verschiedenen Strukturen denn charakterisieren?
Die Metrik wäre in beiden Fällen die selbe oder?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 22. Aug 2021 22:50 Titel: Re: Universum endlich oder unendlich? |
|
|
| Aruna hat Folgendes geschrieben: | | Gibt es für ein euklidisches und unendliches Universum das sich ausdehnt eine Veranschaulichung? |
Ein unendlich ausgedehntes Gummituch, das gedehnt wird.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 22. Aug 2021 22:54 Titel: |
|
|
| Erster Admiral hat Folgendes geschrieben: | Worin genau würde sich denn der Torus mathematisch vom unendlichen euklidischen Raum unterscheiden?
Bzw. anhand welcher Eigenschaft kann man die verschiedenen Strukturen denn charakterisieren?
Die Metrik wäre in beiden Fällen die selbe oder? |
Letzteres ja, die Metrik als lokale geometrische Eigenschaft ist identisch.
Zu Ersterem liegt die Antwort in topologischen Eigenschaft. Auf dem flachen Torus gibt es geschlossene Linien, die überall gerade sind. Siehe auch oben die Windungszahlen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Aruna
Anmeldungsdatum: 28.07.2021
Beiträge: 795
|
| Aruna Verfasst am: 23. Aug 2021 00:26 Titel: Re: Universum endlich oder unendlich? |
|
|
| TomS hat Folgendes geschrieben: | | Aruna hat Folgendes geschrieben: | | Gibt es für ein euklidisches und unendliches Universum das sich ausdehnt eine Veranschaulichung? |
Ein unendlich ausgedehntes Gummituch, das gedehnt wird. |
Okay, und wie bekomme ich das mit der Vorstellung eines Urknalls zusammen bei dem zu Beginn das Gummituch wohl eher noch nicht unendlich ausgedehnt war?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 23. Aug 2021 07:44 Titel: Re: Universum endlich oder unendlich? |
|
|
| Aruna hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Aruna hat Folgendes geschrieben: | | Gibt es für ein euklidisches und unendliches Universum das sich ausdehnt eine Veranschaulichung? |
Ein unendlich ausgedehntes Gummituch, das gedehnt wird. |
Okay, und wie bekomme ich das mit der Vorstellung eines Urknalls zusammen bei dem zu Beginn das Gummituch wohl eher noch nicht unendlich ausgedehnt war? |
So wie hier beschrieben: FAQ - unendliches Universum trotz Urknall?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Günther
Anmeldungsdatum: 23.11.2010
Beiträge: 305
|
| Günther Verfasst am: 23. Aug 2021 09:23 Titel: |
|
|
| Aruna hat Folgendes geschrieben: |
Okay, und wie bekomme ich das mit der Vorstellung eines Urknalls zusammen bei dem zu Beginn das Gummituch wohl eher noch nicht unendlich ausgedehnt war? |
Doch, war es.
Die Regionen, die man jeweils dem "beobachtbarem Universum" zuordnet sind endlich. Unendlich viele davon - und das Universum war auch beim Urknall räumlich unendlich.
|
|
|
Schmu
Anmeldungsdatum: 23.06.2021
Beiträge: 112
|
| Schmu Verfasst am: 23. Aug 2021 20:34 Titel: |
|
|
|
Das sind doch wieder nur mathematische Spitzfindigkeiten. Egal, ich frage mich aber schon wieso das Universum nach dem Urknall nicht isotropisch sein soll, Gummituch?!? Also die Explosionen die ich so kenne sind isotropisch.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 23. Aug 2021 23:23 Titel: |
|
|
| Schmu hat Folgendes geschrieben: | | Das sind doch wieder nur mathematische Spitzfindigkeiten. |
Nein, präzise Modelle.
| Schmu hat Folgendes geschrieben: | | Egal, ich frage mich aber schon wieso das Universum nach dem Urknall nicht isotropisch sein soll … |
Ich habe nicht gesagt, dass das Universum nicht isotrop ist, sondern dass Modelle existieren, denen zufolge es nicht isotrop wäre und die aufgrund der Beobachtungen nicht ausgeschlossen werden können.
| Schmu hat Folgendes geschrieben: | | Also die Explosionen die ich so kenne sind isotropisch. |
Eine Explosion ist aber nur isotrop um genau einen Punkt, um keinen anderen. Sie ist insbs. inhomogen. Das unterscheidet eine Explosionen ganz grundsätzlich vom Urknall.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Schmu
Anmeldungsdatum: 23.06.2021
Beiträge: 112
|
| Schmu Verfasst am: 23. Aug 2021 23:34 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Nein, präzise Modelle. |
Ja ich meinte insb. das mit dem Torus.
| Zitat: |
Eine Explosion ist aber nur isotrop um genau einen Punkt, um keinen anderen. Sie ist insbs. inhomogen. Das unterscheidet eine Explosionen ganz grundsätzlich vom Urknall. |
Wäre der Urknall nicht ein kleines bisschen inhomogen hätte sich das Universum direkt wieder selbst vernichtet aber offensichtlich war ja etwas mehr Materie als Antimaterie vorhanden.
Nun ist jedoch ein "Gummituch" deutlich nicht isotrop wie erklärt sich das denn dann?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 23. Aug 2021 23:49 Titel: |
|
|
| Schmu hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: |
Nein, präzise Modelle. |
Ja ich meinte insb. das mit dem Torus. |
Was ist denn daran spitzfindig?
Alle wesentlichen kosmologischen Modelle gehen davon aus, dass das Universum auf genügend großen Skalen homogen und isotrop ist. Aber ein 3-Torus ist gerade auf großen Skalen explizit nicht isotrop und verletzt damit diese wesentliche Annahme.
Darüberhinaus sind kompakte, flache Modelle wie der 3-Torus ernstzunehmende Modelle; es gibt schlicht keinen Grund, sie auszuschließen.
| Schmu hat Folgendes geschrieben: | | Nun ist jedoch ein "Gummituch" deutlich nicht isotrop … |
Irgendwie missverstehen wir uns; das Gummituch ist in jedem Punkt isotrop.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Schmu
Anmeldungsdatum: 23.06.2021
Beiträge: 112
|
| Schmu Verfasst am: 24. Aug 2021 00:20 Titel: |
|
|
|
Ich glaub wir reden aneinander vorbei, wenn das Universum homogen ist hätten sich ja nie Strukturen wie Galaxien gebilded. Und mit Torus hatten ich immer Bugs und Abstürze naja liegt vielleicht an mir egal. Aber isotrop wäre doch ein Gummiball nicht ein Gummituch?
|
|
|
Aruna
Anmeldungsdatum: 28.07.2021
Beiträge: 795
|
| Aruna Verfasst am: 24. Aug 2021 05:51 Titel: |
|
|
| Schmu hat Folgendes geschrieben: | | Aber isotrop wäre doch ein Gummiball nicht ein Gummituch? |
Das Gummituch war die Antwort auf einem Frage meinerseits nach einer Veranschaulichung.
Ein flaches Gummituch ist eine 2D-Veranschaulichung eines flachen höherdimensionalen Raums, z.B. eines 3D-Raums.
Dieses Gummituch ist in der Veranschaulichung gedacht eingebettet in einen 3D-Raum, so dass ich mir seine Flachheit überhaupt vorstellen kann, oder eben die Krümmung z.B. einer 2D-Kugeloberfäche, bei der die Kugelform in 3D erkennbar ist.
Entsprechend kann ein Gummituch in 2D, also der Welt, die es in der Veranschaulichung beschreibt, isotrop sein.
Ich meine, Deine Aussage, ein Gummituch wäre nicht isotrop, bezieht sich darauf, dass Du die Ebene des Gummituchs verlässt und dich in 3D außerhalb
des Gummituchs begibst, wo dann das Gummituch nicht vorhanden ist.
So das Gummituch aber das Universum - in dem Bild der Anschaulichkeit wegen ein 2D-Universum - darstellt, also "Alles", kannst Du das Gummituch aber nicht nach oben oder nach unten verlassen.
Ein 3D-Gummiball wäre in einem höherdimensionalen Raum, in der man den Gummiball in einer vierten Dimension verlassen könnte, auch nicht isotrop.
Einen endlichen Gummiball kann man schon in drei Dimensionen verlassen bzw. an der Grenze des Gummiballs zum Raum ohne Gummiball eine klare Richtungsabhängigkeit erkennen.
Ein unendlich ausgedehnter Gummiball könnte isotrop sein, aber bei einem unendlich ausgedehnten Objekt stelle ich mir die Frage, ob man einen unendlich ausgedehnten Ball, also wohl einer Kugel, von einem unendlich ausgedehnten Würfel oder sonstigem Objekt unterscheiden kann.
(Für die Antwort braucht man wahrscheinlich "mathematische Spitzfindigkeiten".)
Naja zumindest ich kann mir zwar noch die zeitliche Ausdehnung eines 3D-Raums zumindest lokal vorstellen, aber bei der Vorstellung einer Krümmung komme ich an meine Grenzen.
Daher ist die Veranschaulichung in zwei Dimensionen, also ein Gummituch oder eine Gummifläche, eben deutlich anschaulicher als die Vorstellung eines
3D-Gummiraums, dessen Krümmung ich mir gar nicht vorstellen kann und daher auch keinen Unterschied zwischen gekrümmt oder nicht gekrümmt
oder einem isotropen euklidischen Raum, der endlich ist und einem isotropen euklidischen Raum, der nicht endlich ist.
Ich hab schon Schwierigkeiten, mir vorzustellen, dass eine 2D-Torusobefläche euklidisch ist.
Bei der Oberfläche eines geraden Rohrs (wenn das sich unendlich dünn vorstellt und daher den Kanten an den Enden keine Fläche zugesteht) ist mir das einigermaßen klar, weil ich das in der Vorstellung längs aufschneiden kann und dann flach auf den Tisch legen.
Um aus einem Rohr einen Torus zu formen, müsste ich IMO das Rohr allerdings biegen (krümmen?), also den Anteil der Rohrfläche die beim Torus das innere "Loch" begrenzt stauchen und den Anteil der Rohrfläche, die beim Torus nach außen später nach außen zeigt, dehnen.
Wieso bleiben bei diesem Vorgang (bzw. dieser Konstruktion) Parallelen, die sich über beide Flächenanteile erstrecken parallel oder die Winkelsumme von Dreiecken, die sich über beide Flächenanteile erstrecken, 180°? 
Zuletzt bearbeitet von Aruna am 24. Aug 2021 07:33, insgesamt 2-mal bearbeitet |
|
|
Aruna
Anmeldungsdatum: 28.07.2021
Beiträge: 795
|
| Aruna Verfasst am: 24. Aug 2021 06:53 Titel: Re: Universum endlich oder unendlich? |
|
|
| TomS hat Folgendes geschrieben: | | Aruna hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Aruna hat Folgendes geschrieben: | | Gibt es für ein euklidisches und unendliches Universum das sich ausdehnt eine Veranschaulichung? |
Ein unendlich ausgedehntes Gummituch, das gedehnt wird. |
Okay, und wie bekomme ich das mit der Vorstellung eines Urknalls zusammen bei dem zu Beginn das Gummituch wohl eher noch nicht unendlich ausgedehnt war? |
So wie hier beschrieben: FAQ - unendliches Universum trotz Urknall? |
Danke. :-)
Damit ich die Struktur der Antwort verstehe:
Mir scheint, in Argumentation B.) stehen die Kugelschalen, außer, dass die eben zu ihrer Zeit die genannte Bedingung erfüllen, in keinem Zusammenhang.
Also man kann nicht sagen, dass ein Ort (oder ein mitbewegter Beobachter an diesem Ort) auf einer so zum Zeitpunkt t1 definierten Kugelschale sich zum Zeitpunkt t2 auf der Kugelschale, die die Konstruktionsbedingung zum Zeitpunkt t2 erfüllt, befindet?
Sonst müssten sich ja in einem sich ausdehnenden Universum zu "Beginn" beliebig getrennte Beobachter aufeinander zu bewegen?
Ist das gemeint mit:
| Zitat: | | Diese Kugelschalen darf man sich nicht als etwas Physikalisches vorstellen! Es ist nur eben so, dass man diese Schar von Kugelschalen definieren kann, und dass die Orte, die auf diesen Kugelschalen liegen, auch existieren. |
?
Dass solche Kugelschalen existieren, ist aber doch nur erlaubt, wegen
| Zitat: |
Die Radialkoordinate r ist als Koordinate für alle Zeiten t einschließlich der Zeit t = 0 unbeschränkt, d.h. es gibt keine maximale Radialkoordinate; insofern ist das Universum gewissermaßen unendlich.
|
wäre r beschränkt, wäre ich ja auch in der Konstruktion der Kugelschalen beschränkt?
Oder soll die Kugelschalenkonstruktion gerade zeigen, dass sich mit dem entsprechenden Skalenfaktor eins FRW-Universums eben die Unbeschränktheit dieses Universums zu allen Zeiten ergibt?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 24. Aug 2021 08:00 Titel: |
|
|
| Schmu hat Folgendes geschrieben: | | … wenn das Universum homogen ist … |
Das bestreitet niemand; es geht nicht um perfekte Isotropie. Deswegen:
| TomS hat Folgendes geschrieben: | | Alle wesentlichen kosmologischen Modelle gehen davon aus, dass das Universum auf genügend großen Skalen homogen und isotrop ist. Aber ein 3-Torus ist gerade auf großen Skalen explizit nicht isotrop und verletzt damit diese wesentliche Annahme. |
| Schmu hat Folgendes geschrieben: | | … Aber isotrop wäre doch ein Gummiball nicht ein Gummituch? |
Das gilt nur, wenn du die Modelle „von außen“ = aus der Perspektive des einbettenden Raumes betrachtest, aber so geht die Mathematik nicht vor. Man betrachtet die Mannigfaltigkeit = das Gummituch ausschließlich „von innen“ ohne einbettenden Raum. Und dabei sind sowohl Gummiball als auch unendlich ausgedehntes Gummituch homogen und isotrop. Da wir aber über verschwindende Krümmung reden, ist der Gummiball ausgeschlossen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 24. Aug 2021 08:27 Titel: Re: Universum endlich oder unendlich? |
|
|
| Aruna hat Folgendes geschrieben: | Ist das gemeint mit:
| Zitat: | | Diese Kugelschalen darf man sich nicht als etwas Physikalisches vorstellen! Es ist nur eben so, dass man diese Schar von Kugelschalen definieren kann, und dass die Orte, die auf diesen Kugelschalen liegen, auch existieren. |
?
|
Genau.
| Aruna hat Folgendes geschrieben: | Dass solche Kugelschalen existieren, ist aber doch nur erlaubt, wegen
| Zitat: |
Die Radialkoordinate r ist als Koordinate für alle Zeiten t einschließlich der Zeit t = 0 unbeschränkt, d.h. es gibt keine maximale Radialkoordinate; insofern ist das Universum gewissermaßen unendlich.
|
wäre r beschränkt, wäre ich ja auch in der Konstruktion der Kugelschalen beschränkt? |
Genau.
| Aruna hat Folgendes geschrieben: | | Oder soll die Kugelschalenkonstruktion gerade zeigen, dass sich mit dem entsprechenden Skalenfaktor eins FRW-Universums eben die Unbeschränktheit dieses Universums zu allen Zeiten ergibt? |
Ja. Zu allen Zeiten größer Null.
Die Konstruktion zeigt, dass folgende beiden Aussagen nicht im Widerspruch zueinander stehen:
1) für beliebig kleine Zeiten t > 0 existieren Orte, deren Abstand zueinander beliebig groß sein kann
2) Orte, deren Abstand für eine Zeit t > 0 beliebig groß jedoch endlich ist, haben im Grenzfall t = 0 auch den Abstand Null
Dabei ist eben essentiell, dass physikalische Abstände nicht identisch mit Koordinatendifferenzen sind.
Salopp gesprochen:
1) das Universum war bereits unmittelbar nach dem Urknall und natürlich für spätere Zeiten unendlich
2) ein heute beliebig großer Bereich war beim Urknall ein ausdehnungsloser Punkt
Es geht nur darum, derartige Aussagen zu präzisieren.
EDIT: ich wollte nichts zu Beobachtern sagen, weil dies erstens irrelevant ist, und weil ich zweitens nicht überprüfen wollte, ob die Orte überhaupt einer erlaubten Trajektorie entsprechen - oder evtl. zu Überlichtgeschwindigkeiten führen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
| Ich Verfasst am: 24. Aug 2021 10:24 Titel: |
|
|
Man sollte erwähnen, dass hier im Thread zwar "Universum" gesagt wird, aber eigentlich über das mathematische Friedmann-Modell gesprochen wird. Dessen Aussagen insbesondere über den Urknall und die Zeit direkt danach sind problematisch. Man geht stattdessen von einer Inflationsphase aus, die das heute beobachtbare Universum erzeugt hat.
Die absolute Homogenität auf großen Skalen ist auch eine Eigenschaft des Modells und nicht notwendigerweise des realen Universums. Auch eine hinreichend große Explosion sähe z.B. lokal wie ein Friedmann-Universum aus, und Szenarien wie die "eternal inflation" sehen das beobachtbare Univrersum als Teil einer vom Inflatonfeld "auskonsdensierten" Blase.
Da man nur das beobachtbare Universum kennt und auch keine zuverlässigen physikalischen Theorien für die Entstehung des Universums hat, kann man eigentlich nicht viel über die tatsächliche Struktur des Universums sagen. Nur eben, dass der beobachtbare Teil davon recht gut von einem Friedmann-Modell beschrieben werden kann.
|
|
|
Schmu
Anmeldungsdatum: 23.06.2021
Beiträge: 112
|
| Schmu Verfasst am: 24. Aug 2021 12:59 Titel: |
|
|
| Aruna hat Folgendes geschrieben: |
Daher ist die Veranschaulichung in zwei Dimensionen, also ein Gummituch oder eine Gummifläche, eben deutlich anschaulicher als die Vorstellung eines 3D-Gummiraums, dessen Krümmung ich mir gar nicht vorstellen kann und daher auch keinen Unterschied zwischen gekrümmt oder nicht gekrümmt |
Achso, jetzt versteh ich was mit Gummituch gemeint ist.
Ich würd mir das so vorstellen wie eine Höhle in der Spinnen wohnen und die da kreuz und quer ihre Netze reingebaut haben, wenn man da was reinwirft bleibts irgendwo hängen und dehnt Netze aber egal so richtig vorstellen kann man sich das nicht, hast recht.
| Zitat: |
Ich hab schon Schwierigkeiten, mir vorzustellen, dass eine 2D-Torusobefläche euklidisch ist.
Bei der Oberfläche eines geraden Rohrs (wenn das sich unendlich dünn vorstellt und daher den Kanten an den Enden keine Fläche zugesteht) ist mir das einigermaßen klar, weil ich das in der Vorstellung längs aufschneiden kann und dann flach auf den Tisch legen.
Um aus einem Rohr einen Torus zu formen, müsste ich IMO das Rohr allerdings biegen (krümmen?), also den Anteil der Rohrfläche die beim Torus das innere "Loch" begrenzt stauchen und den Anteil der Rohrfläche, die beim Torus nach außen später nach außen zeigt, dehnen.
Wieso bleiben bei diesem Vorgang (bzw. dieser Konstruktion) Parallelen, die sich über beide Flächenanteile erstrecken parallel oder die Winkelsumme von Dreiecken, die sich über beide Flächenanteile erstrecken, 180°? |
Ring fand ich war immer die bessere Lösung als so blöder Torus.
|
|
|
willyengland
Anmeldungsdatum: 01.05.2016
Beiträge: 676
|
| willyengland Verfasst am: 24. Aug 2021 13:23 Titel: |
|
|
Dass das Universum isotrop sei, hat mir noch nie eingeleuchtet. Wo man auch hinguckt, immer gibt es "Verklumpungen" unterbrochen von "Nichts". Selbst auf größten Skalen ist das so, z.B. "Great Wall" etc.
_________________
Gruß Willy |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 24. Aug 2021 13:26 Titel: |
|
|
Noch zwei Anmerkungen:
Die Friedmann-Modelle setzen perfekte Homogenität und Isotropie voraus; das tatsächlich sichtbare Universum ist natürlich nicht perfekt homogen und isotrop, man darf sich jedoch (zunächst) vorstellen, dass es sozusagen einem Friedmann-Universum plus kleinen Dichte-Fluktuationen gleicht.
Einige Modelle für das gesamte Universum verletzen die Annahme der Homogenität und Isotropie, z.B. das o.g. Torus-Universum. Dabei handelt es sich nicht um kleine Fluktuationen, sondern um eine vollständig andere Form bzw. Topologie. Ein flaches Friedmann-Universum, also ein euklidischer 3-Raum, und ein 3-Torus unterscheiden sich global; dennoch würde der lokal sichtbare Ausschnitt eines 3-Torus dem eines euklidischen 3-Raum gleichen; die beiden Modelle wären lokal ununterscheidbar (wenn der 3-Torus nicht klein genug wäre und wir z.B. die Andromeda-Galaxie fünffach sehen könnten).
Es wird natürlich nicht einfacher, wenn - wie von Ich beschrieben - dieses Universum wiederum nur ein kleiner Ausschnitt eines Multiversums wäre.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Schmu
Anmeldungsdatum: 23.06.2021
Beiträge: 112
|
| Schmu Verfasst am: 24. Aug 2021 13:48 Titel: |
|
|
| willyengland hat Folgendes geschrieben: | | Dass das Universum isotrop sei, hat mir noch nie eingeleuchtet. Wo man auch hinguckt, immer gibt es "Verklumpungen" unterbrochen von "Nichts". Selbst auf größten Skalen ist das so, z.B. "Great Wall" etc. |
Also isotrop heisst doch unabhänging von der Richtung? Also ein Stern stahlt in alle Richtungen gleichmässig ab das heisst ja nicht das er innen drinn homogen ist, also so hab ich das verstanden.
Das mit den Verklumpungen ist eh merkwürdig das geht ja nur zu erklären mit der dunklen Materie die sich deutlich früher von der Strahlung abgekoppelt haben muss sonst hätte man in der Zeit bis jetzt garnicht solche Strukturen bilden können mit den riesigen Leerräumen.
|
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 24. Aug 2021 13:54 Titel: |
|
|
| willyengland hat Folgendes geschrieben: | | Dass das Universum isotrop sei, hat mir noch nie eingeleuchtet. Wo man auch hinguckt, immer gibt es "Verklumpungen" unterbrochen von "Nichts". Selbst auf größten Skalen ist das so, z.B. "Great Wall" etc. |
Ja, eben egal, wo man hinguckt... Natürlich ist das Universum höchstens statistisch homogen und isotrop. Daß irgendwelche Verklumpungen in jeder Richtung existieren, ist deshalb eigentlich zu erwarten. Die Frage ist also eher, ob bestimmte Strukturen statistisch signifikant von der Annahme der Isotropie abweichen. Für einige, auch die Great Wall, scheint es da keinen Konsens zu geben.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 24. Aug 2021 15:26 Titel: |
|
|
| Zitat: | | Ich hab schon Schwierigkeiten, mir vorzustellen, dass eine 2D-Torusobefläche euklidisch ist. |
Das funktioniert auch nicht, wenn man sich den Torus Eingebettet in den dreidimensionalen Raum vorstellt. Deswegen gehen Mathematiker und Physiker anders vor: man geht aus von der flachen, euklidischen Ebene und kompaktifiziert diese.
Die Verzerrung ist lediglich für die Veranschaulichung notwendig und tritt rechnerisch nicht auf.
| Beschreibung: |
| https://de.m.wikipedia.org/wiki/Periodische_Randbedingung |
|
| Dateigröße: |
99.03 KB |
| Angeschaut: |
3914 mal |
|
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 24. Aug 2021 15:32, insgesamt 6-mal bearbeitet |
|
|
willyengland
Anmeldungsdatum: 01.05.2016
Beiträge: 676
|
| willyengland Verfasst am: 24. Aug 2021 15:27 Titel: |
|
|
Man sagt dann immer: Jaaa, man muss eben auf NOCH größeren Skalen gucken.
Alle Skalen die ich kenne, sind jedenfalls nicht isotrop.
Mein Zimmer - nicht isotrop
Mein Planet - nicht isotrop
Mein Sonnensystem - nicht isotrop
Meine Galaxie - nicht isotrop
Meine lokale Gruppe - nicht isotrop
...
_________________
Gruß Willy |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 24. Aug 2021 15:36 Titel: |
|
|
Das ist im hier diskutierten Kontext dennoch irrelevant, solange auf genügend großen Skalen weiterhin gilt, dass ein flaches, homogenes und isotropes Universum plus kleine Dichtefluktuationen vorliegt.
Es geht um die Frage des endlichen oder unendlichen Universums. Kleine Verformungen ändern daran nichts.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 24. Aug 2021 16:23 Titel: |
|
|
Zur Mathematik der Kompaktifizierung.
Man definiert auf der euklidischen Ebene E² mittels zweier nicht kollinearer Gittervektoren
und zweier natürlichen Zahlen
mittels der Gitterpunkte
ein Gitter
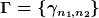
Nun identifiziert man Punkte mit Vektoren p, q auf der Ebene mittels
Anschaulich gesprochen bedeutet dies, dass man alle Punkte p auf der Ebene in die erste Gitterzelle abbildet.
Statt des euklidischen Abstandes auf der Ebene
 = |p-q|^2)
verwendet man
 = \min\limits_{\gamma \in \Gamma}|(p-q)-\gamma|^2)
Damit schreibt man kurz für den Torus
Als Beispiel betrachten wir ein quadratisches Gitter der Kantenlänge Eins, d.h. mit Gittervektoren (1,0) und (0,1). Die Abbildung eines Punktes auf die erste Gitterzelle liefert zum Beispiel
 = (0.7; 0.4) - 1 \cdot (1; 0) + 3 \cdot (0; 1) \to (0.7; 0.4))
Die Abstandsberechnung für zwei Punkte (0.1; 0.1) und (0.1; 1.2) liefert auf der Ebene
^2 + (1.2 - 0.1)^2 = 1.1^2)
Nach Kompaktifizierung beträgt der Abstand auf dem Torus jedoch
^2 + ((1.2 - 1) - 0.1)^2 = 0.1^2)
Die Koordinate 1.2 wird in die erste Zelle und damit die Koordinate 0.2 abgebildet.
Nochmal für die zwei Punkte (0.1; 0.1) und (0.1; 0.9) auf der Ebene
^2 + (0.9 - 0.1)^2 = 0.8^2)
und auf dem Torus
^2 + ((0.9 - 1) - 0.1)^2 = 0.2^2)
Es ist kürzer, von 0.1 nach -0.1 = 0.9-1 nach links zu laufen, als von 0.1 nach rechts zu 0.9 fast um den ganzen Torus herum.
Das "min" in der Abstandsformel bedeutet: lege die Punkte p und q in die erste Gitterzelle, berechne für p,q sowie ihre Entsprechungen in den benachbarten Gitterzellen die Abstände und nehme davon den kleinsten. :teufel:
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Günther
Anmeldungsdatum: 23.11.2010
Beiträge: 305
|
| Günther Verfasst am: 25. Aug 2021 17:57 Titel: |
|
|
| index_razor hat Folgendes geschrieben: | | Die Frage ist also eher, ob bestimmte Strukturen statistisch signifikant von der Annahme der Isotropie abweichen. Für einige, auch die Great Wall, scheint es da keinen Konsens zu geben. |
Soweit mir bekannt ist das kein Problem, wenn man die Skala hinreichend groß wählt. All das ist ein Resultat der Verklumpung. Schaut man vorher nach, findet man beim CMB Temperaturabweichungen in der Größenordnung 10^-3 K.
|
|
|
oxi:)
Gast
|
| oxi:) Verfasst am: 29. Aug 2021 23:38 Titel: |
|
|
Hallo, nachdem mir bereits bei einem anderen Thema so kompetent geholfen wurde, möchte ich hier nochmal gerne eine andere Frage loswerden, die mit dem Thema zusammenhängt.
Neulich habe ich gelesen, dass in einem unendlichen Universum unendlich viele Kopien von uns existieren. So gesehen würde ich also gerade unendlich oft in diesem Universum eine Frage in dieses Forum schreiben. Doch muss das wirklich so sein? Ich fände das sehr befremdlich! Oder kann es uns auch nur einmal im unendlichen Universum geben?
|
|
|
Aruna
Anmeldungsdatum: 28.07.2021
Beiträge: 795
|
| Aruna Verfasst am: 30. Aug 2021 07:11 Titel: |
|
|
| oxi:) hat Folgendes geschrieben: |
Neulich habe ich gelesen, dass in einem unendlichen Universum unendlich viele Kopien von uns existieren. So gesehen würde ich also gerade unendlich oft in diesem Universum eine Frage in dieses Forum schreiben. Doch muss das wirklich so sein? Ich fände das sehr befremdlich! Oder kann es uns auch nur einmal im unendlichen Universum geben? |
Kannst Du Dich erinnern, wo Du das gelesen hast, oder die genaue Argumentation, warum das so sein soll?
Unendlich ist natürlich ziemlich groß, da werden auch Ereignisse mit Wahrscheinlichkeiten nahe 0 sicher auftreten und wenn die Möglichkeiten Materie anzuordnen endlich wäre, klingt es plausibel, dass sich bestimmte Anordnungen bei unendlich viel Materie wiederholen, einige unendlich oft.
Die Frage ist, ob sich alle unendlich oft wiederholen.
Naja, "unendlich" führt zu merkwürdigen Phänomenen. In einem anderen Forum wurde z.B. auf das Banach-Tarski-Paradoxon hingewiesen:
| Zitat: | Das Banach-Tarski-Paradoxon oder auch Satz von Banach und Tarski ist eine Aussage der Mathematik, die demonstriert, dass sich der anschauliche Volumenbegriff nicht auf beliebige Punktmengen verallgemeinern lässt. Danach kann man eine Kugel in drei oder mehr Dimensionen derart zerlegen, dass sich ihre Teile wieder zu zwei lückenlosen Kugeln zusammenfügen lassen, von denen jede denselben Durchmesser hat wie die ursprüngliche. Das Volumen verdoppelt sich, ohne dass anschaulich ersichtlich ist, wie durch diesen Vorgang Volumen aus dem Nichts entstehen können sollte. Dieses Paradoxon demonstriert, dass das mathematische Modell des Raumes als Punktmenge in der Mathematik Aspekte hat, die sich in der physischen Realität nicht wiederfinden.
https://de.wikipedia.org/wiki/Banach-Tarski-Paradoxon |
und das Lee Smolin in dem Buch "The Trouble with Physics" (ich hab es nicht gelesen und kenne den Kontext nicht) geschrieben habe, "dass eine Theorie, in der unendliche Grössen auftauchen, nur eine fehlerhafte Beschreibung der Realität liefern kann."
Unendlichkeit führt zumindest mich an die Grenzen meiner Vorstellungskraft, siehe hier im Thread das für alle Zeiten t>0 unendlich ausgedehnte, expandierende Gummituch, auf dem aber jeder für t>0 beliebig große endliche Abstand für t->0 gegen 0 konvergiert, oder Hilberts Hotel:
https://www.youtube.com/watch?v=toF6zL8QodA
daher wäre die genaue Begründung, warum das so sein, und welches Modell verwendet wurde, IMO hilfreich, sofern es hier anderen nicht wohlbekannt ist.
Zuletzt bearbeitet von Aruna am 30. Aug 2021 07:19, insgesamt 2-mal bearbeitet |
|
|
oxi:)
Gast
|
| oxi:) Verfasst am: 30. Aug 2021 07:17 Titel: |
|
|
Hallo,
Ich hatte dies in einem zugegeben populärwiss. Artikel mal gelesen. Zudem wird auch im deutschen Wikipedia Artikel zum Universum auf derartige Überlegungen hingewiesen.
|
|
|
Aruna
Anmeldungsdatum: 28.07.2021
Beiträge: 795
|
| Aruna Verfasst am: 30. Aug 2021 07:41 Titel: |
|
|
| oxi:) hat Folgendes geschrieben: | Hallo,
Ich hatte dies in einem zugegeben populärwiss. Artikel mal gelesen. Zudem wird auch im deutschen Wikipedia Artikel zum Universum auf derartige Überlegungen hingewiesen. |
Ah, da gibt es ja Quellenangaben:
| Zitat: | In neuerer Zeit hat u. a. der Physiker Max Tegmark behauptet, dass aus dem gegenwärtigen Standardmodell des Universums zusammen mit der Quantentheorie folge, dass im Durchschnitt alle  Meter eine „Zwillingswelt“ existieren müsse.[13] Die von Tegmark genannten Argumente treffen auch auf ein Universum mit endlichem, aber hinreichend großem, Volumen zu. Diese Argumente wie auch die Folgerungen sind allerdings umstritten, und wurden z. B. in der Publikation About the Infinite Repetition of Histories in Space durch den Satz „these scenarios remain no more than literary tales“ beschrieben.[14] |
[13]:
https://arxiv.org/pdf/astro-ph/0302131.pdf
[14]
https://arxiv.org/abs/1301.5295
das les ich dann, wenn ich die Argumentation des Papers im anderen Thread verstanden habe...
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 30. Aug 2021 09:20 Titel: |
|
|
@oxi -
die Grundprobleme derartiger Argumentationen sind a) die diversen ungesicherten oder unklaren Annahmen und b) die Verwendung wahrscheinlichkeitstheoretischer Argumente. Die Problematik bei letzterem ist schlicht, dass es es oft unklar ist, wie der umgangssprachliche Begriff „Wahrscheinlichkeit“ mathematisch präzise definiert werden soll.
Ein Beispiel:
Betrachte die Zahl pi. Man liest oft, dass sie keinem Muster folgt, dass jede Ziffer oder jede Ziffernfolge gleich häufig vorkommt u.ä. Nehmen wir an, dass ein bestimmter Ausschnitt der Welt durch eine unendliche Ziffernfolge (in pi) beschrieben werde - gemäß den Regeln der Quantenmechanik gibt es bereits für ein einzelnes Wasserstoffatom unendlich viele verschiedene mögliche Zustände - und dass die Wahrscheinlichkeit für das Auftreten einer beliebigen unendlichen Ziffernfolge z die Wahrscheinlichkeit p(z) sei.
Die Summe aller Wahrscheinlichkeiten über alle verschiedenen Ziffernfolgen muss gleich Eins sein:
 = 1)
Nehmen wir an, die Wahrscheinlichkeit aller Ziffernfolgen sei identisch:
 = p )
d.h. jede Ziffernfolge z habe die selbe Wahrscheinlichkeit p.
Nun gibt es unendlich viele unendliche Ziffernfolgen, d.h. die unendliche Summe über alle Wahrscheinlichkeiten liefert
Die Annahme
 = p > 0)
führt also auf einen Widerspruch - egal wie klein wir p machen.
Im Grenzfall
 = p = 0)
gilt dann aber
was wiederum auf einen Widerspruch führt.
Die Mathematiker wissen das seit langem. Die Erkenntnis ist, dass es über unendlich vielen Werten z keine Gleichverteilung geben kann, d.h. mittels
kann überhaupt keine konsistente Wahrscheinlichkeit definiert werden; es ist sinnlos, von so etwas zu reden.
Zweites Beispiel:
Nehmen wir wieder an, dass ein bestimmter Ausschnitt der Welt durch eine endliche Ziffernfolge (in pi) beschrieben werde; das obige Problem mit p > 0 für unendlichen Ziffernfolgen tritt so nicht auf. Nun gehen wir schrittweise durch die Dezimaldarstellung von pi und suchen das Auftreten dieser Ziffernfolge; haben wir die gefunden, so gehen wir weiter und suchen alle weiteren Stellen, wo sie auftritt. Ist das der Fall, löschen wir diese Stellen einfach heraus! Damit haben wir eine neue Zahl pi* konstruiert, in der diese Ziffernfolge exakt einmal auftritt. Da es unendlich viele Ziffernfolgen in pi* gibt, wäre die Wahrscheinlichkeit für das Auftreten „Anzahl dieser Ziffernfolge“ / „Anzahl aller Ziffernfolgen“ = 1 / unendlich = 0. Natürlich führt dies zu dem o.g. Problem für p = 0.
D.h. wir haben eine Zahl p* mit unendlich vielen verschiedenen Ziffernfolgen in der die gegebene Ziffernfolge exakt einmal auftritt.
(beide Argumente müsste man noch mathematisch streng formulieren)
Dritter Punkt:
Die Argumente ändern sich, wenn ich die Funktion p(z) explizit angeben kann und wenn die o.g. Summe dann tatsächlich Eins ergibt. Mathematisch ist dies möglich, allerdings hat noch kein Physiker auch nur ansatzweise eine derartige Wahrscheinlichkeit für eine Welt berechnen können. Eine „Welt“ im Sinne der Physik ist etwas völlig anderes als eine strukturell triviale Zahlenfolge; wir haben noch nicht mal eine einigermaßen präzise mathematische Definition, was eine „Welt in einem Multiversum“ ist, wie wir „alle möglichen Welten“ konstruieren, wie wir sie zählen …
Deswegen halte ich diverse Argumente für die mehrfache Existenz von Welten in einem Multiversum für zumindest schwierig.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 30. Aug 2021 09:52, insgesamt einmal bearbeitet |
|
|
oxi:)
Gast
|
| oxi:) Verfasst am: 30. Aug 2021 09:50 Titel: |
|
|
@TomS
Vielen Dank für deine Erläuterung! Dann scheint diese Argumentation ja auch auf ziemlich wackeligen Füßen zu stehen, oder anders gesagt: sie ist hochgradig spekulativ und mitunter ist in der Realität nichts dran.
Ich habe das Argument für das unendliche Vorkommen der Welt im Universum (da war nicht mal vom Multiversum die Rede) in ganz einfacher Form so in Erinnerung: da die Erde existiert, muss die Wahrscheinlichkeit für deren Existenz größer als 0 sein (wobei ich das hier schonbegrifflich schwierig finde, Existenz hängt ja nicht einfach vom Zufall ab). Da aber das Universum unendlich ist und die Wahrscheinlichkeit größer 0, muss sie unendlich oft vorkommen.
Allerdings hab ich mir nur gedacht, dass für eine derartige Argumentation alles wirklich ideal zufällig geschehen muss, was ja sehr streitbar ist.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 30. Aug 2021 10:14 Titel: |
|
|
| oxi:) hat Folgendes geschrieben: | | Ich habe das Argument für das unendliche Vorkommen der Welt im Universum (da war nicht mal vom Multiversum die Rede) in ganz einfacher Form so in Erinnerung: da die Erde existiert, muss die Wahrscheinlichkeit für deren Existenz größer als 0 sein (wobei ich das hier schonbegrifflich schwierig finde, Existenz hängt ja nicht einfach vom Zufall ab). Da aber das Universum unendlich ist und die Wahrscheinlichkeit größer 0, muss sie unendlich oft vorkommen. |
Und genau das ist schwierig.
Wie definiert man die Wahrscheinlichkeit für das Auftreten eines Ereignisses E bzw. “Erdähnlich”? Man zählt für alle Ereignisse N die Ereignisse Z, die E entsprechen, also
= \frac{Z(E)}{N})
sowie in unseren Fall
 = \lim_{N \to \infty} p_N(E))
Man sieht aus dieser Definition, dass
 > 0)
dann und nur dann gilt, wenn
 = \infty)
D.h. wenn man diesen operationalen bzw. frequentistischen Wahrscheinlichkeitsbegriff und das Gesetz der großen Zahlen zugrundelegt, dann muss man in das Argument bereits hineinstecken, dass unendlich viele erdähnliche Planeten vorliegen, um auf eine Wahrscheinlichkeit größer Null zu kommen.
Wenn man die Wahrscheinlichkeit nach Kolmogorow zugrundelegt, dann wird über die Herkunft oder die konkrete Berechnung der Wahrscheinlichkeit nichts gesagt, es werden lediglich axiomatische Aussagen über die Wahrscheinlichkeiten gefordert. Was spricht logisch dagegen, dass es genau einen erdähnlichen Planeten gibt, solange man eine Wahrscheinlichkeit dafür nicht mittels Physik berechnen kann? Kann man heute nämlich nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 30. Aug 2021 10:24, insgesamt einmal bearbeitet |
|
|
oxi:)
Gast
|
| oxi:) Verfasst am: 30. Aug 2021 10:18 Titel: |
|
|
|
Alles klar, dann danke für deine Ausführungen!
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 30. Aug 2021 10:43 Titel: |
|
|
| TomS hat Folgendes geschrieben: | Man zählt für alle Ereignisse N die Ereignisse Z, die E entsprechen, also
sowie in unseren Fall
Man sieht aus dieser Definition, dass
dann und nur dann gilt, wenn
|
Ist das tatsächlich hinreichend? Müsste gemäß L'Hospital nicht zusätzlich
 > 0)
gelten? Oder ist das in obiger Bedingung bereits implizit enthalten?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 30. Aug 2021 10:49 Titel: |
|
|
Du hast recht, die Bedingung ist nicht hinreichend. Für eine asymptotische Reihe muss gelten
 \sim N )
d.h. z.B.
 \sim \ln N )
ist nicht ausreichend.
Aber das Argument brauche ich doch gar nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
Registrieren
Login
FAQ
Suchen
