TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 13. Jul 2016 10:10 Titel: FAQ - unendliches Universum trotz Urknall? TomS Verfasst am: 13. Jul 2016 10:10 Titel: FAQ - unendliches Universum trotz Urknall? |
 |
|
Wie kann es sein, dass wir heute ein unendlich ausgedehntes Universum vorfinden *) obwohl die die Ausdehnung des Universums zum Urknall doch Null war? Muss das Universum nicht schon immer unendlich gewesen sein, um heute unendlich sein zu können? Und wenn ja, widerspricht dies nicht dem Urknall?
Um das zu verstehen muss man die Bedeutungen der Begriffe wie Urknall, unendlich, Ausdehnung Null usw. mathematisch präzisieren. Ich möchte das im Folgenden anhand eines einfachen Beispiels erklären.
Nehmen wir ein unendlich ausgedehntes Universum, nämlich eine spezielle Ausprägung des Friedmann-Robertson-Walker Universums.
Die Metrik, d.h. die Lösung der Einsteinschen Feldgleichungen lautet
\,\left[dr^2 + r^2\,d\Omega^2 \right])
Für eine feste Zeit t > 0 eines mitbewegten Beobachters gilt die 3-Metrik auf einem räumlichen, 3-dim. Schnitt
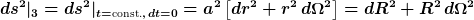
mit
 = a(t)\,r)

D.h. für jede feste Zeit t > 0 liegt ein unendlich ausgedehnter, euklidischer, 3-dim. Raum vor, in dem für räumliche Abstände der normale Satz des Pythagoras gilt **).
Die Radialkoordinate r ist als Koordinate für alle Zeiten t einschließlich der Zeit t = 0 unbeschränkt, d.h. es gibt keine maximale Radialkoordinate; insofern ist das Universum gewissermaßen unendlich.
Allerdings geht in eine Definition von physikalischen, messbaren Abständen auf dieser Ebene der sogenannte Skalenfaktor a(t) ein; die Koordinaten selbst sind lediglich unphysikalische Hilfsgrößen! Setzen wir einem beliebigen Punkt mit Radialkoordinate r = 0 und zeichnen eine Kugelfläche mit Radialkoordinate r = r_0 um diesen Punkt. Die physikalischen Abstände R(t) dieser Kugelfläche vom Mittelpunkt sind dann gegeben durch
 = a(t)\,r_0 )
d.h. der messbare Radius R(t) skaliert mit a(t).
Ein auf dieser Kugelfläche mitbewegter Beobachter mit festem r = r_0 für alle Zeiten t bewegt sich also mit der Zeit vom Mittelpunkt weg bzw. auf diesen zu, je nach Verhalten des Skalenfaktors a(t) ***)
Für den Skalenfaktor a(t) gilt in einem flachen FRW-Universum die Gleichung
 = a_0\,t^\alpha )
mit
})
Der Parameter w beschreibt dabei den Zusammenhang zwischen Energiedichte und Druck und hängt vom Materie- oder Strahlungsinhalt des Universums ab. Im frühen, strahlungsdominierten Universum ist w = 1/3 eine sinnvolle Annahme, d.h.
 = a_0\,\sqrt{t} )
Nun kann man zwei Betrachtungen anstellen, wobei im Grenzfall t gegen Null einmal konvergierende und einmal divergierende Abstände resultieren.
A) Man wähle wie oben eine Kugelschale mit beliebiger, jedoch fester Radialkoordinate r_0. Der physikalisch relevante Abstand vom Mittelpunkt ergibt sich aus der o.g. Lösung zu
 = a(t)\,r_0 = a_0\,r_0\,\sqrt{t} )
Dieser Abstand wird Null für t = 0 und strebt für wachsende Zeit gegen Unendlich. Insofern hatten alle Punkte innerhalb und auf dieser Kugelschale zu Beginn = beim Urknall den physikalischen Abstand R(0) = 0.
 = 0 )
B) Man betrachte für einen festen Zeitpunkt t > 0 eine Kugelschale mit Radialkoordinate

Für variable Zeiten t resultiert daraus eine Schar von Kugelschalen.
Berechnet man nun für jede dieser Kugelschalen den physikalischen Abstand R(t) so findet man
 = a(t)\,r_{t} = a_0\,\sqrt{t} \,\cdot\, r_0 \frac{t _0}{t} = a_0\,r_0\,t_0\frac{1}{\sqrt{t}})
Diese Kugelschalen darf man sich nicht als etwas Physikalisches vorstellen! Es ist nur eben so, dass man diese Schar von Kugelschalen definieren kann, und dass die Orte, die auf diesen Kugelschalen liegen, auch existieren. D.h. man findet für beliebig kleine Zeiten t Kugelschalen, deren physikalische Abstände vom Mittelpunkt im Grenzfall t gegen Null divergieren.
 = \infty)
D.h. dass für beliebig kleine Zeiten t immer Orte existieren, deren physikalischer Abstand voneinander beliebig groß ist. Insofern war dieses Universum zum Urknall für t > 0 immer schon unendlich groß, denn es existiert für keine Zeit t > 0 eine obere Schranke der Abstände R(t).
Man beachte jedoch, dass es sich immer nur um Grenzprozesse handelt, und dass genau genommen für t = 0 keine mathematisch sinnvolle Aussage möglich ist. Bei t = 0 liegt eine Singularität vor ****)
Zusammenfassend: Aus der Argumentation (A) folgt, dass die Abstände zweier physikalischer, mitbewegter Beobachter, die heute einen endlichen Abstand haben, zum Urknall hin gegen Null konvergieren. Aus der Argumentation (B) folgt, dass für beliebig kleine Zeiten hin zum Urknall immer Orte gefunden werden können, deren Abstände beliebig groß sind, die divergieren.
-----------
*) was zwar nicht experimentell gesichert ist, jedoch den gängigen Modellen entspricht und zu den beobachteten Daten passt
**) der so definierte 3-dim. Raum ist euklidisch, also flach, d.h. nicht gekrümmt; die 4-dim. Raumzeit ist jedoch i.A. gekrümmt
***) der zunächst ausgezeichnete Punkt r = 0 ist beliebig, d.h. diese Argumentation zeichnet nicht diesen speziellen Mittelpunkt aus; die Argumentation gilt für beliebig wählbare Mittelpunkte und beliebige Kugelflächen
*****) und man beachte außerdem, dass wir davon ausgehen müssen, dass die Allgemeine Relativitätstheorie nahe dem Urknall keine physikalisch sinnvolle Theorie mehr ist, sondern durch eine noch zu konstruierende Quantengravitationstheorie ersetzt werden muss
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|















