| Autor |
Nachricht |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 31. Jan 2024 11:48 Titel: FAQ - Visualisierungen für Schwarze Löcher TomS Verfasst am: 31. Jan 2024 11:48 Titel: FAQ - Visualisierungen für Schwarze Löcher |
 |
|
Ich möchte im folgenden einige immer wiederkehrenden Fragen zu schwarzen Löchern möglichst anschaulich erklären.
Dabei ist mir wichtig, dass die Mathematik auf ein absolutes Minimum reduziert und die oft verwirrende Index-Notation vermieden wird, zugleich die Beantwortung der Fragen jedoch mathematisch korrekt ist.
Zum zweiten möchte ich insbesondere Größen betrachten, die explizit physikalisch messbar sind. Teilweise resultieren falsche Vorstellungen ausschließlich aus der Tatsache, dass Größen diskutiert werden, für die genau dies nicht zutrifft, die Mann dennoch "veranschaulicht" und damit falsche Vorstellungen zementiert.
Vorab eine kurze Erklärung: Die Geometrie schwarzer Löcher wird häufig für nicht rotierende Exemplare diskutiert, man erhält die so genannte Schwarzschild-Geometrie. Außerhalb des Ereignishorizontes stellt sich die Situation recht einfach dar, wenn man sogenannte Schwarzschild-Koordinaten (t,r) verwendet. Dies sind jedoch lediglich spezielle Koordinaten, die für einen realen Beobachter in der Nähe des Schwarzen Lochs keine direkte physikalische Bedeutung haben.
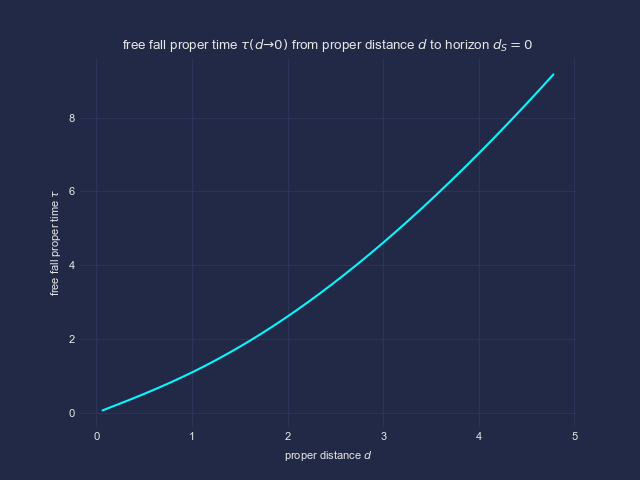
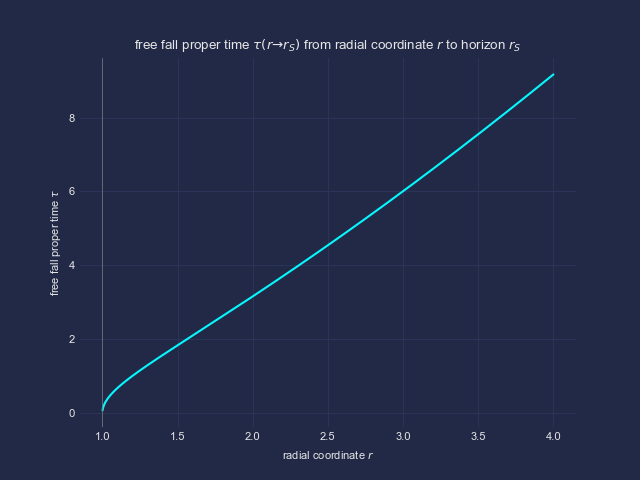
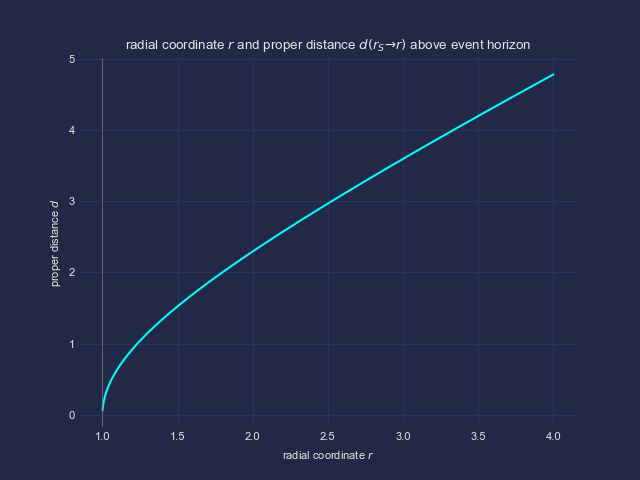
In den Graphiken zeige ich die Zusammenhänge mit zwei anderen, tatsächlich beobachtbaren Größen, nämlich dem invarianten Abstand d vom (der Höhe über) dem Ereignishorizont, sowie der Eigenzeit tau für den freien Fall von einer endlichen Höhe bis zum Ereignishorizont. Ersteres würde auf einem (sehr reißfesten und nicht dehnbaren) Maßband gemessen, letzteres auf der mit dem Astronauten mitfallenden Armbanduhr.
| Beschreibung: |
|
| Dateigröße: |
20.52 KB |
| Angeschaut: |
3998 mal |
|
| Beschreibung: |
|
| Dateigröße: |
20.22 KB |
| Angeschaut: |
3998 mal |
|
| Beschreibung: |
|
| Dateigröße: |
20.53 KB |
| Angeschaut: |
3998 mal |
|
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 09. Feb 2024 18:36, insgesamt 2-mal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 31. Jan 2024 12:40 Titel: TomS Verfasst am: 31. Jan 2024 12:40 Titel: |
 |
|
Erste wirklich spannende Frage: mit welcher Geschwindigkeit überquert ein frei fallender Beobachter den Ereignishorizont?
Zur Antwort: zunächst ist die Frage ist falsch gestellt! Der Horizont stellt die Grenze zweier Bereiche dar: außerhalb gelangen radial nach außen laufende Lichtstrahlen zu immer größeren Abständen und letztlich ins Unendliche; innerhalb gelangen radial "nach außen" *) laufende Lichtstrahlen immer in die Singularität! Auf dem Horizont befindliche Lichtstrahlen sind dort sozusagen gefangen. D.h. jedoch, der Horizont ist eine sogenannte lichtartige Fläche; man darf ihn sich nicht als stationär vorstellen; insbs. definiert er im Rahmen der Relativitätstheorie kein gültiges Bezugssystem.
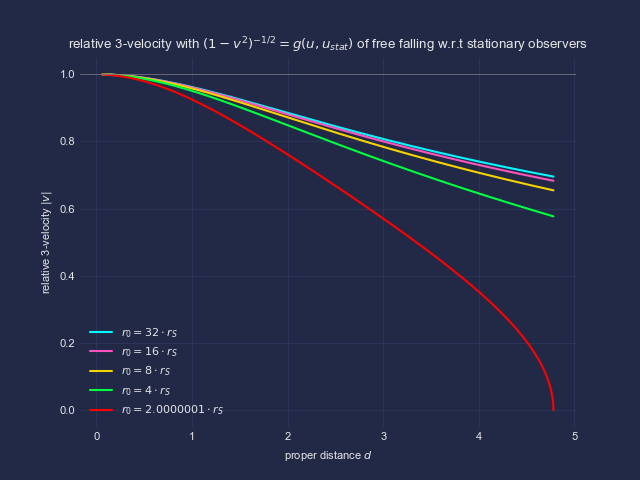
Wir betrachten also zwei Arten von Beobachtern, radial frei fallende Beobachter sowie oberhalb des Horizontes stationäre Beobachter mit festem Abstand zu diesem. Dann berechnen wir die Relativgeschwindigkeit, die ein stationärer Beobachter einem dicht an ihm vorbei fallenden Beobachter zuschreibt. Wir betrachten also eine lokal messbare Größe **)
In der Grafik betrachte ich Beobachter, die aus unterschiedlichen Starthöhen – dort zu Beginn stationär – ins schwarze Loch fallen. Der rote Beobachter startet noch innerhalb der Grafik, alle anderen weiter außerhalb. Auf der x-Achse aufgetragen ist der Abstand der stationären, messenden Beobachters, auf der y-Achse die jeweilige Relativgeschwindigkeiten der frei fallenden Beobachter. Für knapp oberhalb des Ereignishorizontes stationäre, messende Beobachter erreichen alle frei fallenden Beobachter dort fast Lichtgeschwindigkeit. Der Grenzübergang zu einem exakt am Horizont stationären Beobachter ist nicht gestattet; genauso wenig wie die Idee eines solchen innerhalb ***)
*) alternativ: die Richtung "radial nach außen" existiert nicht
**) die Relativgeschwindigkeit eines weit entfernten Objektes ist in der allgemeinen Relativitätstheorie nicht eindeutig definierbar
***) es kann dort keine stationären Beobachter geben, das ist mathematisch ausgeschlossen
| Beschreibung: |
|
| Dateigröße: |
41.96 KB |
| Angeschaut: |
3996 mal |
|
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 09. Feb 2024 18:37, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 02. Feb 2024 17:47 Titel: TomS Verfasst am: 02. Feb 2024 17:47 Titel: |
 |
|
Nächstes Thema, wie vergeht die Zeit?
Aus Sicht eines stationären Beobachters ist der Raumzeit-Punkt, an dem sich ein anderer, frei fallender Beobachter "jetzt" befindet, ja eine rein theoretische Größe, definiert mittels der Eigenzeit des stationären Beobachters, genutzt als Koordinatenzeit für entfernte Ereignisse.
Der frei fallende Beobachter verwendet dagegen seine Eigenzeit für Ereignisse an seinem eigenen Ort; das ist also unmittelbar messbar.
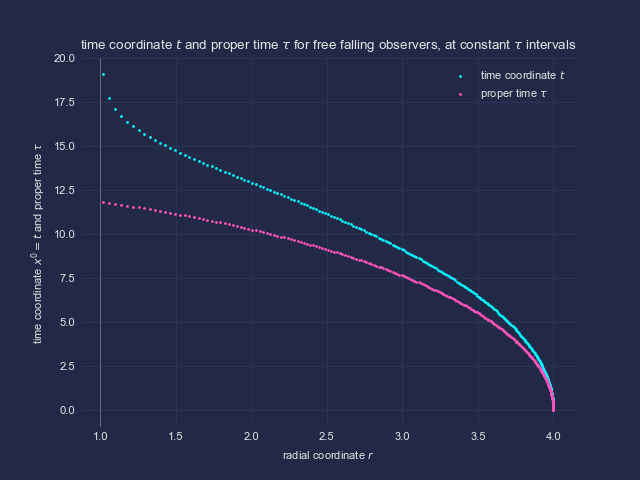
Im Bild dargestellt ist die Weltlinie eines (von einem gewissen Abstand * und dort zunächst in Ruhe) frei fallenden Beobachters sowie die regelmäßigen Ticks auf einer von ihm mitgeführten Uhr. Auf der y-Achse aufgetragen ist einmal seine Eigenzeit tau sowie die dem jeweiligen Punkt der Raumzeit zugeschriebene Eigen- = Koordinatenzeit des (bei *) stationären Beobachters.
Der frei fallende Beobachter erreicht und überquert den Horizont in endlicher Eigenzeit. Diese endlich vielen Ticks seiner Uhr divergieren jedoch gemessen in der Zeit des stationären Beobachters. Der selbe Tick erscheint bei der selben Radialkoordinate auf der x-Achse.
Was der stationären Beobachter tatsächlich sieht im Folgebeitrag.
| Beschreibung: |
|
| Dateigröße: |
24.31 KB |
| Angeschaut: |
3995 mal |
|
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 09. Feb 2024 18:38, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 04. Feb 2024 21:37 Titel: TomS Verfasst am: 04. Feb 2024 21:37 Titel: |
 |
|
Nun zu den Beobachtungsdaten.
Ein Beobachter B und eine Sonde S befinden sich beim selben Abstand zum Schwarzen Loch. Die Ticks der Uhren sind synchronisiert. Die Sonde S stürzt frei in Richtung schwarzem Loch. Alle N Ticks sendet sie ein Lichtsignal identischer Frequenz an B. Sie korrigiert dabei die Dopplerverschiebung relativ zu einem (hypothetischen) jeweils lokal bei ihr befindlichen Beobachter, so dass im folgenden lediglich die gravitative Rotverschiebung relevant ist.
Der Beobachter B empfängt die Signale der Sonde S in immer größeren zeitlichen Abständen. Die zunehmende Entfernung von S und somit die zunehmende Lichtlaufzeit ist wenig relevant; maßgeblich ist die gravitative Zeitdilatation (wie im letzten Beitrag erkennt man, dass die Koordinatenzeit des Aussendens bei S divergiert).
Außerdem erscheinen die Signale von S bei B zunehmend rotverschoben.
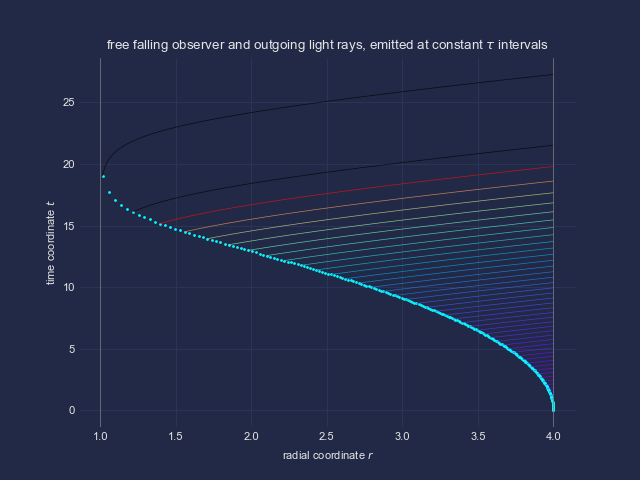
In der Graphik sind Weltlninie von B und S erkennbar, ebenso die der Lichtsignale. Jedes Signal wird im fernen violetten Bereich abgestrahlt; die Weltlinie sind mit der bei B wahrgenommen Farbe eingefärbt; die Verschiebung ins Infrarote mit schwarzen Weltlinien.
| Beschreibung: |
|
| Dateigröße: |
41.83 KB |
| Angeschaut: |
3994 mal |
|
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 09. Feb 2024 18:39, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 06. Feb 2024 10:27 Titel: TomS Verfasst am: 06. Feb 2024 10:27 Titel: |
 |
|
Zuletzt noch eine Darstellung der so genannten Spaghettifizierung.
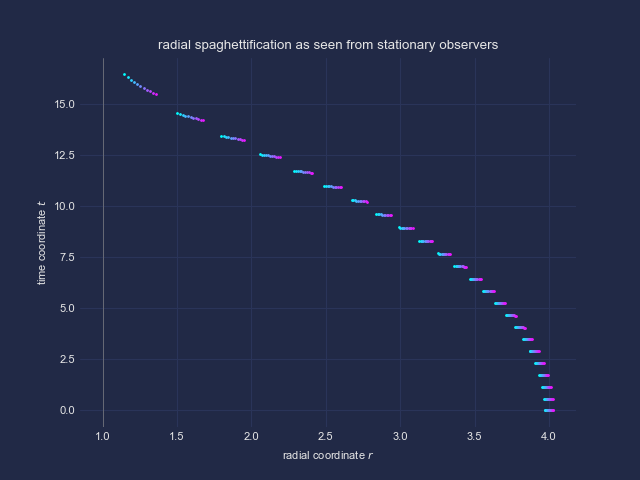
Ein Körper, der frei in ein schwarzes Loch stürzt, wird aufgrund von Gezeitenkräften mit zunehmender Annäherung immer stärker radial gedehnt. Ich zeige das anhand einer zu Beginn nahe beieinander befindlichen Gruppe loser (d.h. nicht miteinander verbundener) Objekte und deren Geodäten hin zum schwarzen Loch.
Auf der x-Achse ist wieder die Radiakordinate aufgetragen. Ein jeweils dort befindlicher stationärer Beobachter sieht die Gruppe der direkt bei ihm vorbeifallenden Objekte. Näher am schwarzen Loch befindliche Beobachter sehen eine größere radiale Ausdehnung der Gruppe.
Dies gilt ist auch messbar durch einen mit den Objekten mitbewegten, fallenden Beobachter; es handelt sich nicht um einen Scheineffekt.
| Beschreibung: |
|
| Dateigröße: |
20.64 KB |
| Angeschaut: |
3991 mal |
|
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 09. Feb 2024 18:40, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 09. Feb 2024 15:26 Titel: TomS Verfasst am: 09. Feb 2024 15:26 Titel: |
 |
|
Ich hatte vor einiger Zeit schon mal die Lösung der Wellengleichung in der Schwarzschild Geometrie diskutiert. Passt hier auch ganz gut rein.
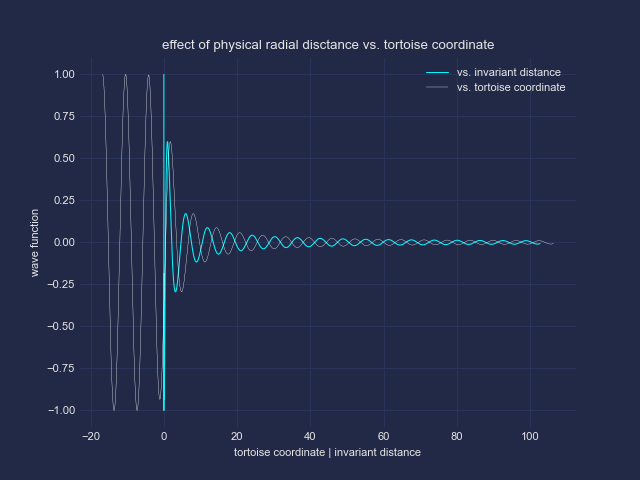
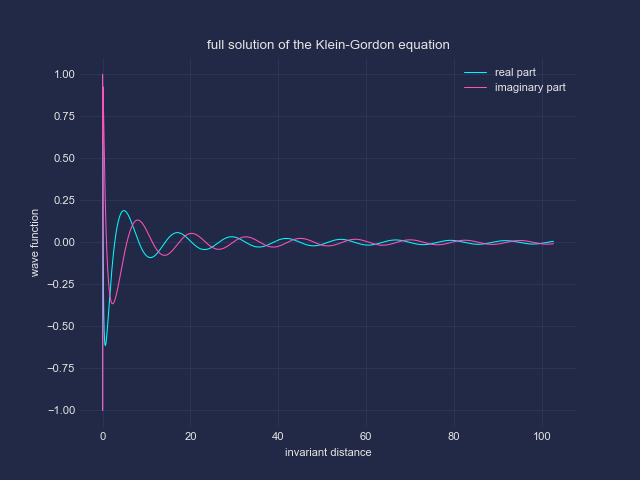
Zuerst betrachten wir die Lösung der Wellengleichung für Real und Imaginärteil eines masselosen Skalarfeldes *) Man erkennt zunächst den starken, radialen Abfall wie bei einer Kugelwelle – hier natürlich zusätzlich unter dem Einfluss der Gravitation.
Anschließend betrachten wir den Einfluss der Wahl der Radialkoordinate. In einer geeigneten anderen Koordinate wird der Horizont ins negativ Unendliche verschoben. Man erkennt, dass die bis dorthin laufenden Oszillationen bei Transformation zum invarianten Abstand in einen endlichen Bereich oberhalb des Horizontes "gepresst" werden; in jedem beliebig kleinen Bereich oberhalb des Horizontes liegen demnach unendlich viele Oszillation.
*) die Maxwell-Gleichungen für elektromagnetische Wellen wären komplizierter, liefern jedoch keine wesentlichen neuen Einsichten.
| Beschreibung: |
|
| Dateigröße: |
40.72 KB |
| Angeschaut: |
3987 mal |
|
| Beschreibung: |
|
| Dateigröße: |
30.02 KB |
| Angeschaut: |
4028 mal |
|
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 09. Feb 2024 18:42, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 09. Feb 2024 15:36 Titel: TomS Verfasst am: 09. Feb 2024 15:36 Titel: |
 |
|
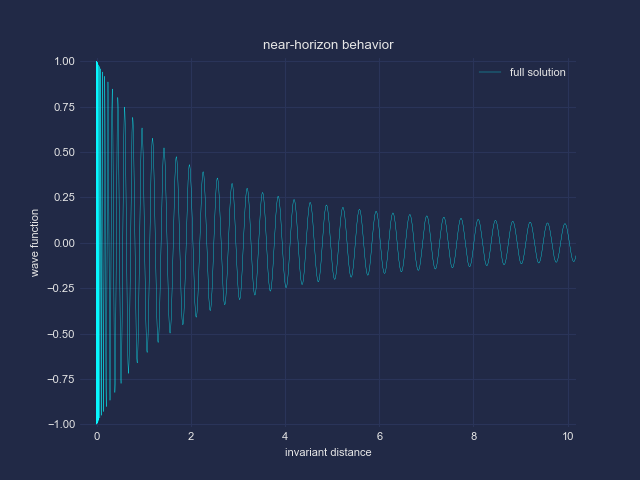
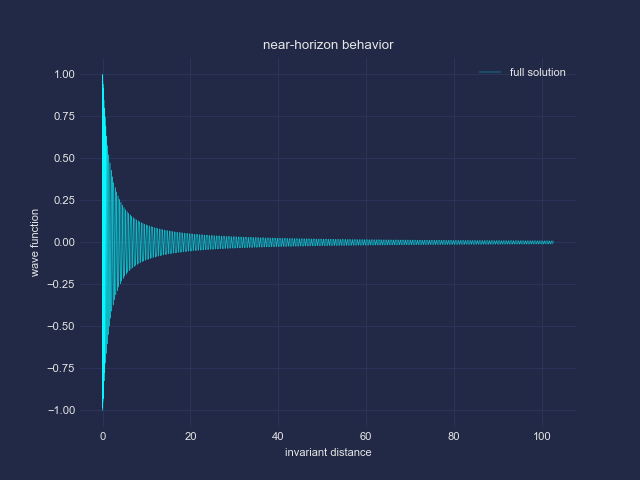
In den nächsten beiden Bildern habe ich den Bereich am Horizont hinein-gezoomt.
| Beschreibung: |
|
| Dateigröße: |
41.06 KB |
| Angeschaut: |
3990 mal |
|
| Beschreibung: |
|
| Dateigröße: |
32.11 KB |
| Angeschaut: |
4019 mal |
|
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 09. Feb 2024 18:41, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 09. Feb 2024 15:43 Titel: TomS Verfasst am: 09. Feb 2024 15:43 Titel: |
 |
|
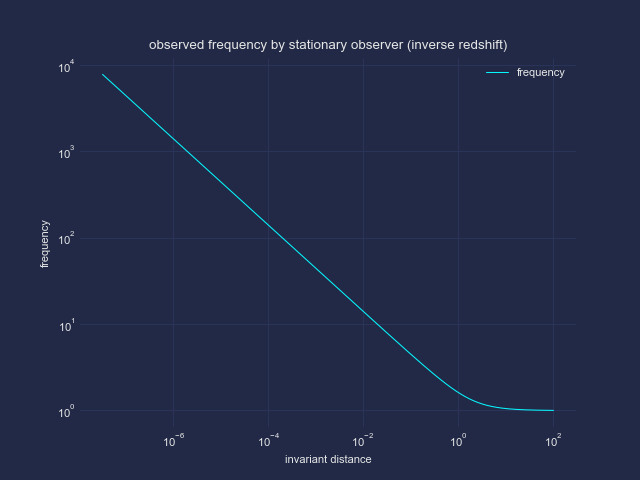
Zuletzt habe ich mittels zweier Methoden, die Blau- bzw. Rotverschiebung berechnet.
1) direkt mittels der bekannten Formel
2) mittels der Wellenlänge, bestimmt aus den Nulldurchgängen der Schwingung.
Natürlich müssen beide Ergebnisse identisch sein.
Der Witz ist, dass in der neu eingeführten Radialkoordinate, die komplizierte Wellengleichung auf einer gekrümmten Raumzeit durch eine Wellengleichung auf einer flachen Raumzeit plus einem kleinen Korrekturterm ersetzt wird; letzterer erscheint wie ein klassisches Potenzial. Für genügend kleine Wellenlängen ist dieser Zusatzterm über eine Wellenlänge näherungsweise konstant, man kann im wesentlichen eine einfache ebene Welle ansetzen und deren Wellenlänge bestimmen. Daraus folgt letztlich die Frequenz. Zur Berechnung physikalischer Größen muss man jedoch beachten, dass Wellenlänge und Frequenz in speziellen Koordinaten errechnet wurden, so dass zuletzt noch auf eine invariante Messgröße – aus Sicht eines bei einem gewissen Abstand stationären Beobachters – umgerechnet werden muss.
Erledigt man dies, so reproduziert die Methode (2) im Rahmen kleiner numerischer Ungenauigkeiten die bekannten Ergebnisse von Methode (1).
Das interessante daran ist, dass es keine wirkliche Wechselwirkung der Wellenausbreitung mit der Geometrie gibt, die Raumzeit "quetscht" oder "streckt" die Welle nicht; sie ist in gewisser Weise frei, genauso wie ein kräftefrei bewegter Beobachter. Blau- bzw. Rotverschiebung sind letztlich Effekte der Transformation zwischen verschiedenen Koordinatensystemen auf beobachtbare Größen für spezielle Beobachter.
| Beschreibung: |
|
| Dateigröße: |
21.51 KB |
| Angeschaut: |
3985 mal |
|
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|



























