| Autor |
Nachricht |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 16. Feb 2024 09:09 Titel: FAQ - Zeitdilatation, Längenkontraktion, lineare Algebra TomS Verfasst am: 16. Feb 2024 09:09 Titel: FAQ - Zeitdilatation, Längenkontraktion, lineare Algebra |
 |
|
Anbei nochmal eine etwas andere Darstellung zur Zeitdilatation und Längenkontraktion. Die Idee ist, beides in ähnlicher Weise darzustellen.
Zeitdilatation
Die Zeitdilatation folgt praktisch aus der Messung eines Zeitintervalls entlang der Weltlinie eines Objektes auf einer mitgeführten Uhr. Im folgenden sei diese der Einfachheit halber gerade. Zur Parametrisierung der Weltlinie verwende ich Koordinaten
 = (t, 0))
d.h. das betrachtete Objekt ruht bei x = 0
Ich schreibe die Weltlinie allgemein als
 = x^\mu(0) + \tau \, u^\mu)
hier speziell als
 = (0,0) + \tau \cdot (1, 0))
d.h. als Geradengleichung mit Parameter tau.
 )
ist dabei ein zeitartiger Einheitsvektor, d.h. die Bewegung des Objektes durch die Raumzeit, hier speziell nur durch die Zeit.
Die Lösung ist in diesem Fall trivialerweise
Die Länge der Strecke vom Start- zum Zielpunkt entspricht gerade tau; während t hier eine Koordinate bezeichnet, die Eigenzeit tau entspricht gerade der invarianten Länge; bitte Koordinatenzeit t und Eigenzeit tau auseinanderhalten!
Nun betrachte ich eine Weltlinie
 = (t, vt))
d.h. ich führe einen Beobachter ein, der sich mit Vierergeschwindigkeit
)
entlang dieser Weltlinie durch die Raumzeit bewegt. Dies ist wieder ein zeitartiger Einheitsvektor, da
 = 1)
Die Geradengleichung
 = x^\mu(0) + \tau \, u^\mu)
lautet nun
 = (0,0) + \tau \, \gamma_v \cdot (1, v))
mit der Lösung


Wieder erscheint die Lösung ziemlich trivial.
Interessant ist, dass ich zur Berechnung nie das Ruhesystem des mit v bewegten Beobachters genutzt habe; die Berechnung von tau ist in jedem beliebigen Koordinatensystem möglich. Der Witz dabei ist wie gesagt, dass wir Koordinate t und Eigenzeit tau unterscheiden; t transformiert sich unter Lorentz-Transformation (die wir hier für t und x nicht betrachtet haben) tau ist dagegen invariant (Beweis kann ich nachliefern).
Irgendwie sieht es so aus, als würde ich die Zeitdilatation hineinmogeln, indem ich gamma einführe. Das ist aber kein Hineinmogeln, sondern die mathematische Formulierung der Invarianz der Lichtgeschwindigkeit. Letztlich steckt dies in der Definition des Einheitsvektors u:
 = \gamma_v \cdot (1, v) )
^2 - (u^1)^2 = \gamma_v^2 \, (1 - v^2) = 1)
Dieser verallgemeinerte Betrag ist invariant unter Lorentz-Transformation; im Falle von Licht folgt daraus die Invarianz von c (hier c=1, d.h. Geschwindigkeiten v in Einheiten von c). Aus dieser Forderung folgt insbs. die Form der Lorentz-Transformation und letztlich die gesamte SRT.
Zuletzt bearbeitet von TomS am 16. Feb 2024 10:55, insgesamt 2-mal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 16. Feb 2024 10:08 Titel: TomS Verfasst am: 16. Feb 2024 10:08 Titel: |
 |
|
Längenkontraktion
Anstelle einer Weltlinie betrachte ich nun zwei, die z.B. Anfang und Ende eines ruhenden Stabes bezeichnen:
)
)
Anstelle der Weltlinie eines Beobachters führe ich eine raumartige Richtung e sowie eine invariante (!) Länge lambda mittels
 = x^\mu(0) + \lambda \, e^\mu)
ein.
Hier speziell weise der Einheitsvektor
)
vom Anfang zum Ende des Stabes, d.h. die Geradengleichung wird zu
 = a^\mu + \lambda \, e^\mu)
 = (t, 0) + \lambda \cdot (0, 1))
mit der trivialen Lösung

lambda wurde definiert im Ruhesystem des Stabes; die beiden Stabenden wurden zu gleichen Zeiten betrachtet, der Einheitsvektor hat keine zeitartige Komponente. D.h. lambda entspricht der invarianten Ruhelänge des Stabes.
Der raumartige Einheitsvektor steht senkrecht auf dem im vorigen Beitrag eingeführten zeitartiger Einheitsvektor, d.h.

Nun betrachte ich wieder die obige Weltlinie
 = (t, vt))
d.h. ich führe wieder den Beobachter ein, der sich mit Vierergeschwindigkeit
)
entlang dieser Weltlinie durch die Raumzeit bewegt. Zu diesem zeitartigen Einheitsvektor konstruiere ich den raumartige orthogonalen Einheitsvektor
)
wobei
 = 0)
gilt.
Dieser bezeichnet die für den bewegten Beobachter gültige Gleichzeitigkeitsrichtung.
Die oben diskutierte Geradengleichung wird zu
 = a^\mu + \lambda_v \, e^\mu)
 = (t_1, 0) + \lambda_v \, \gamma_v \cdot (v, 1))
Die Lösung für die x-Komponente lautet


d.h. der Parameter lambda misst nun eine um den gamma-Faktor verkürzte Länge.
Für die t-Komponente findet man

d.h. aus Sicht des Ruhesystem des Stabes wird ein "Abstand" zwischen zwei Raumzeitpunkten gemessen, die unterschiedliche Zeiten haben (was aufgrund der Form des Einheitsvektors zu erwarten war).
Analog zur Zeitdilatation erscheint die gemessene Länge nicht als Koordinate sondern als Parameter der Geradengleichung; damit handelt es sich wiederum um eine invariante Größe (Beweis folgt).
Anmerkungen
Letztlich ist all dies eine Konsequenz der Geometrie, nämlich der Definition der beiden Einzeitsvektoren und ihrer Orthogonalität. Mathematisch ist dies ausreichend: Die Forderung des Skalarproduktes zweier Vektoren x und y mittels ihrer Komponenten

und damit die Invarianz unter Poincare- anstelle von Galilei-Transformationen (d.h. Lorentz-Transformationen und Translationen) ist der einzige geometrische Input, den es für die SRT braucht.
Historisch betrachtet war die Forderung der Invarianz der Lichtgeschwindigkeit zentral; diese folgt unmittelbar aus lichtartigen Weltlinien
 )

_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 16. Feb 2024 12:09, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 16. Feb 2024 11:22 Titel: TomS Verfasst am: 16. Feb 2024 11:22 Titel: |
 |
|
Zur Invarianz von Messgrößen
Warum reite ich darauf so herum?
1. Weil es m.E. zentral für das Verständnis der SRT und den Einstieg in die ART ist, dass Messgrößen Invarianten sind, d.h. sich bei Koordinatentransformationen nicht ändern, und dass letztere lediglich ein rechentechnisches Hilfsmittel darstellen, jedoch im Kern wenig zur Physik beitragen. Andersrum betrachtet verstellt der Blick auf Koordinaten, Indizes und Lorentz-Transformation den Blick auf's wesentliche.
2. Weil der Wechsel zwischen verschiedenen Beobachtbarn nicht identisch ist mit dem Wechsel des Koordinatensystems. Ich habe oben die Vierergeschwindigkeiten verschiedener Beobachter
 )
betrachtet, jedoch immer im selben Koordinatensystem; natürlich könnte ich auch das Ruhesystem dieser Beobachter betrachten, aber es ist hier völlig unnötig.
D.h. Zeitdilatation und Längenkontraktion handeln von Messungen invarianter Größen. Quellen, die etwas anderes behaupten, sind zumindest schlampig oder irreführend.
A) Zum Beweis der Invarianz der Längenkonteahtion
folgende Beobachtung: Wir benötigen die Weltlinien der Enden des Stabes sowie die Geradengleichung

definiert mittels des Gleichzeitigkeits-Einheitsvektors eines Beobachters.
Die zu messende Länge folgte mittels Lösung dieser linearen Gleichung.
Die Lorentz-Transformation für sämtliche Vektoren a, b, e …

(alle anderen analog) entspricht einer Multiplikation Matrix * Vektor; sie ist linear und überführt das Gleichungssystem

in
 = 0)
Die Messgröße lambda wird nicht transformiert, ihr Wert ist invariant. Das ist letztlich lineare Algebra, nämlich eine Äquivalenzumformung des Gleichungssystems.
B) Zum Wechsel des Beobachters
Anwendung der Lorentz-Transformation ausschließlich für die mit dem messenden Beobachter verknüpften Vektoren u und e, nicht jedoch für die Weltlinien a, b

führt auf

Das ist keine Äquivalenzumformung sondern schlicht ein anderes Gleichungssystem; demzufolge hat es eine andere Lösung und liefert für eine andere Messgröße bzw. einen anderen Beobachter einen anderen Wert.
Die Verwirrung stammt wohl daher dass in beiden Fällen die Lorentz-Transformation verwendet wird. Sie wird jedoch unterschiedlich angewandt, einmal als Äquivalenzumformung für das selbe Problem – identische Weltlinien, identische Beobachter, identische Messgröße mit identischem Wert – lediglich in neuen Koordinaten, einmal echt nicht als Äquivalenzumformung sondern zur Definition eines geänderten Problem – identische Weltlinien, neuer Beobachter, neue Messgröße mit anderem Wert – in den alten Koordinaten.
Résumé
Zwischen zwei Ereignissen an zwei Raumzeitpunkten P und Q kann ein eindeutiger invarianter Abstand
)
mittels der Geradengleichung

definiert werden.
In Spezialfällen führt dies auf die Zeitdilatation sowie auf die Längenkontraktion.
Zum Abschluss ein einfaches Analogon aus der Newtonschen Mechanik. Wir betrachten den Auffahrunfall eines Autos mit Geschwindigkeit v auf ein stehendes Fahrzeug mit Geschwindigkeit w=0.
A) Galilei-Invarianz besagt, dass wir die relevanten Energien und den resultierenden Schaden in beliebigen Bezugsystemen berechnen können, aus Sicht des stehenden Fahrzeugs, oder aus Sicht eines vorbeifahrenden Fahrzeugs mit Geschwindigkeit u. Wir subtrahieren einfach von allen Geschwindigkeiten v,w diese Geschwindigkeit u. Für die Geschwindigkeitsdifferenz gilt v-w = (v-u)-(w-u).
B) Oder wir betrachten ein anderes Auto mit einer kleineren Geschwindigkeit v'=v-u, das auf das selbe stehende Auto mit w=0 aufprallt. Das liefert einer kleinere Geschwindigkeitsdifferenz v'-w = (v'-u)-w und somit einen kleineren Schaden.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 21. Feb 2024 00:12 Titel: TomS Verfasst am: 21. Feb 2024 00:12 Titel: |
 |
|
Anbei ein paar Überlegungen zur Realität der Zeitdilatation. Siehe Diskussionen und Quellen hier: https://en.wikipedia.org/wiki/Bell%27s_spaceship_paradox
Vorab, ich halte folgende immer wieder zu findende Argumentation für irreführend und physikalisch nicht schlüssig: Man betrachte zwei in einem Inertialsystem zu Beginn ruhende Raumschiffe mit Abstand L; die Raumschiffe starten gleichzeitig und beschleunigen gleich stark, so dass ihr räumlicher Abstand im Ruhesystem
 = x_1(t) - x_2(t) = L)
konstant bleibt:
 - v_2(t) = 0)
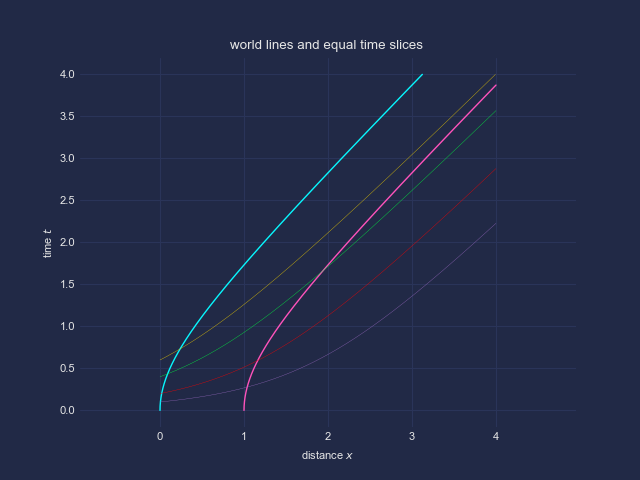
Nun bestimme man die Gleichzeitigkeitslinie im mitbewegten, instantenen Ruhesystem des Raumschiffs 1 und berechne entlang dieser Linie den raumartigen Abstand zum zweiten Raumschiff ... Das ist sinnlos! Ausgehend von der Weltlinie des Raumschiffs 1 findet man einen Schnittpunkt dieser Linie mit der Weltlinie von Raumschiff 2; die Gleichzeitigkeitslinie von Raumschiff 1 ist jedoch in diesem zweiten Schnittpunkt keine Gleichzeitigkeitslinie von Raumschiff 2. Sie ist auch entlang einer tatsächlichen realistierten Verbindung (Seil …) zwischen den Raumschiffen in keinen Punkt eine Gleichzeitigkeitslinie. Die Konstruktion ist willkürlich und inkonsistent.
Ich berechne im folgenden eine physikalisch sinnvolle Verbindungslinie und entlang dieser Linie den Abstand der beiden Raumschiffe.
Wir gehen aus von der Gleichzeitigkeitslinie bzgl. eines bewegten Systems; diese lautet in einem bestimmten Punkt
 = (\bar{t}_0, \bar{x}_0 + \bar{\xi}))
Im Ruhesystem lautet sie
 = \Lambda^{\mu}_{\;\nu} \, \bar{x}^\mu(\bar{\xi}) = (t_0, x_0) + \gamma_v \, (v\,\xi, \xi))

Nun betrachten wir zwei infinitesimal benachbarte Punkte entlang einer Verbindungslinie und fordern, dass die Verbindung für beide Punkte eine Gleichzeitigkeitslinie darstellt. Letztlich betrachten somit in jeden Punkt entlang der Verbindungslinie die Richtung
 \, d\xi)
Daraus folgt
 \, dx)
Das passt zur graphischen Darstellung im Minkowski-Diagramm, wobei die lokale Steigung der Weltlinie

gegeben ist, die lokale Steigung der Gleichzeitigkeitslinie durch

Integrieren wir diese Gleichung, so erhalten wir
 )
Damit ist diese Verbindungslinie in jedem ihrer Punkte (t,x) eine Gleichzeitigkeitslinie der Weltlinie in diesem Punkt, d.h. mit v(t).
Die Funktion v(t) ist aber für alle betrachteten Weltlinien, d.h. Punkte entlang der Verbindung identisch, wenn wir fordern, dass der Abstand aus Sicht eines Beobachters im Ruhesystem immer konstant bleibt.
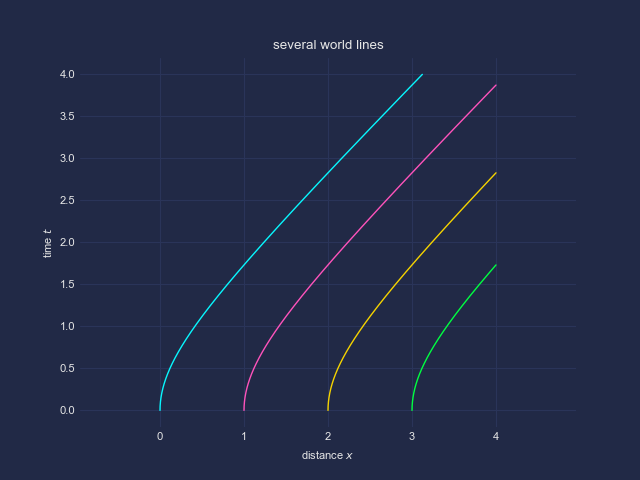
In den Graphiken habe ich Weltlinien konstanter Eigenbeschleunigungen betrachtet, d.h. im jeweiligen momentanen Inertialsystem des bewegten Beobachters ist dessen gemessene Beschleunigung (Trägheitskraft) konstant.
https://en.wikipedia.org/wiki/Hyperbolic_motion_(relativity)
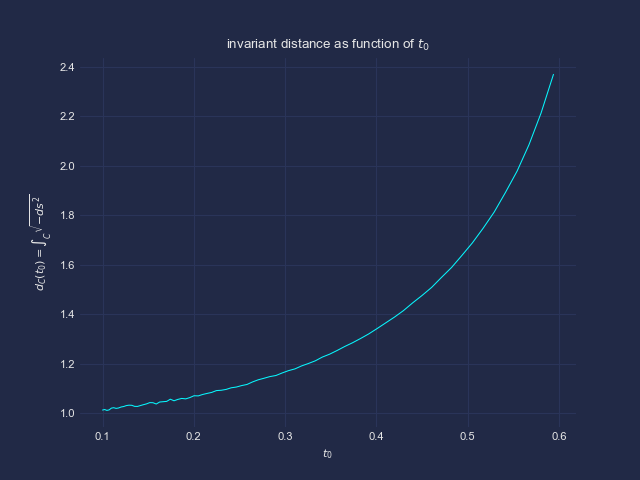
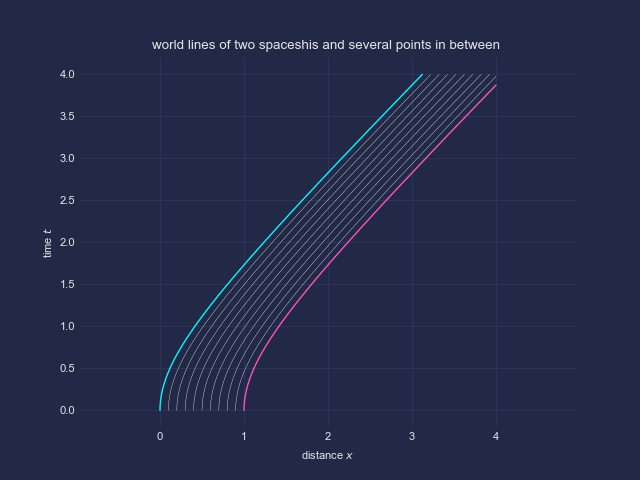
Die invariante Länge einer Verbindungslinie folgt aus der Integration entlang der Verbindungslinie. Dies entspricht im mitbewegten System gerade der Integration über die lokale Ruhelänge, d.h.
 = \int_C \sqrt{-ds^2} = \int_{x_0}^x dx^\prime \sqrt{1-v^2(x^\prime)} = \int_{t_0}^t dt^\prime \, v^{-1} (t^\prime) \, \sqrt{1-v^2(t^\prime)} )
Die Integrationsgrenzen folgen aus den Schnittpunkten der beiden Weltlinien mit der Gleichzeitigkeitslinie.
Betrachtet man den Startpunkt als Funktion der Startzeit, und somit auch den zweiten Schnittpunkt als Funktion so ist
 \to L_\text{inv}(t))
und
}{dt} > 0)
Diese invariante *) Länge ist also nach meinen Berechnungen keine Erhaltungsgröße **) entlang der Weltlinien. Die Schlussfolgerung bzgl. des Raumschiff-Paradoxons, der Abstand nähme zu, ist demnach im wesentlichen korrekt, was nach meinen Überlegungen jedoch aufgrund einer physikalisch sinnvollen Verbindungslinie und eines invarianten Abstandsbegriffs folgt – nicht aus der Längenkontraktion.
Es resultieren somit einige interessante Konsequenzen.
Die willkürlich von Raumschiff 1 aus extrapolierte Gleichzeitigkeit ist irrelevant. Die tatsächlich relevante Gleichzeitigkeit folgt aus der obigen Konstruktion. Da die invariante Länge dieser Verbindung bei identischer Beschleunigung für 1 und 2 nicht konstant bleiben kann, folgt die Unmöglichkeit ideal starrer Körper, die als Ganzes beschleunigt werden können (im vorliegenden Fall z.B. eine Stange zwischen den Raumschiffen). Das vordere Raumschiff fliegt dem hinteren sozusagen davon.
Wenn nun jedoch für die Endpunkte eines Körpers jeweils konstante Eigenbeschleunigung vorliegen soll, dann muss der vordere Endpunkt eine geringere Eigenbeschleunigung als der hintere aufweisen, damit die Eigenlänge konstant bleibt. Dies gilt natürlich entsprechend für alle Punkte auf der Verbindungslinie, demzufolge ist die Eigenbeschleunigung entlang der Verbindungslinie nicht konstant.
Die genaue Berechnung dieses Beschleunigungsprofils entlang der Verbindungslinie habe ich mir noch nicht im Detail angesehen.
*) invariante Größe = ändert sich nicht bei Wechsel des Bezugs- bzw. Koordinatensystems
*) Erhaltungsgröße = ist zeitlich konstant
| Beschreibung: |
| zwei Weltlinien, plus Gleichzeitigkeits-Verbindungslinien |
|
| Dateigröße: |
37 KB |
| Angeschaut: |
4900 mal |
|
| Beschreibung: |
| zwei Weltlinien, plus Weltlinien entlang der Verbindungslinie |
|
| Dateigröße: |
43.49 KB |
| Angeschaut: |
4900 mal |
|
| Beschreibung: |
|
| Dateigröße: |
28.44 KB |
| Angeschaut: |
4900 mal |
|
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 23. Feb 2024 06:09, insgesamt 15-mal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 21. Feb 2024 13:15 Titel: TomS Verfasst am: 21. Feb 2024 13:15 Titel: |
 |
|
to do
Motivation, insbs. Beobachter vs. Koordinaten, Invarianten
Zusammenhang verschiedener Darstellungen
einfache Tensoralgebra (eigener FAQ-Beitrag)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|