| Autor |
Nachricht |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18095
|
 TomS Verfasst am: 31. März 2023 09:29 Titel: FAQ - Energieerhaltung im Fall destruktiver Interferenz |
 |
|
Ich möchte im folgenden kurz erklären, dass sich destruktive Interferenz und Energieerhaltung nicht widersprechen. Als Beispiel verwende ich ein reelles (ungeladenes) masseloses und freies Skalarfeld, das der Klein-Gordon-Gleichung genügt. Dies entspricht weitgehend den einzelnen Komponenten des Vektorpotentials für das elektromagnetisches Feld, unter Verwendung der Strahlungseichung.
Konstruktion der Lösung
Interferenz soll dergestalt vorliegen, dass das Feld innerhalb eines größeren Raumbereiches vollständig verschwindet. Dazu betrachte ich zwei gegenläufig einlaufende Wellenpakete, die sich zu einem bestimmten Zeitpunkt gegenseitig auslöschen (der Fall einer stationären Lösung ist trivial, da für ein stationäres Feld auch die Energiedichte stationär ist, d.h. die Gesamtenergie sicher erhalten). Zur Konstruktion der Wellenpakete verwende ich eine Eigenschaft masseloser Felder, die sowohl für das Skalarfeld als auch für das elektromagnetische Feld gilt: die Dispersionsrelation ist linear, die Form eines Wellenpaketes bleibt unter Zeitentwicklung erhalten, d.h. es findet kein Zerfließen statt. Dies folgt unmittelbar aus der Wellengleichung
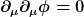
(\partial_t - \partial_x))
Die Lösungen für rechts- bzw. links-laufende Wellenpakete der Form
 = f(x \pm t) )
für eine beliebige Funktion f zulässt.
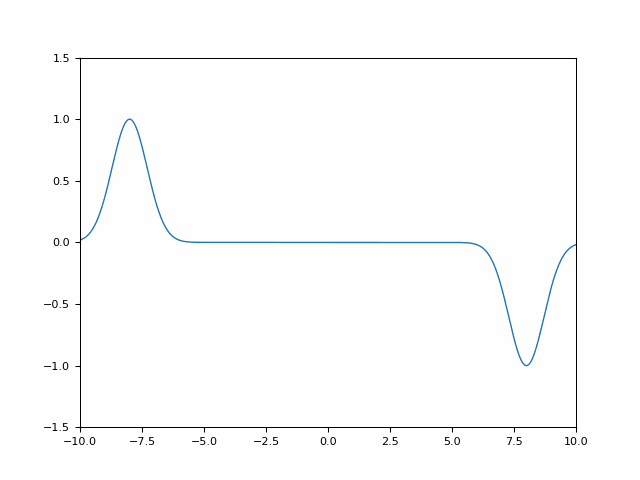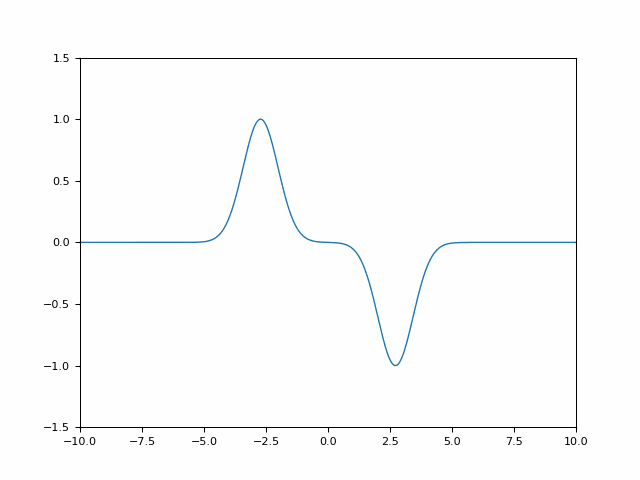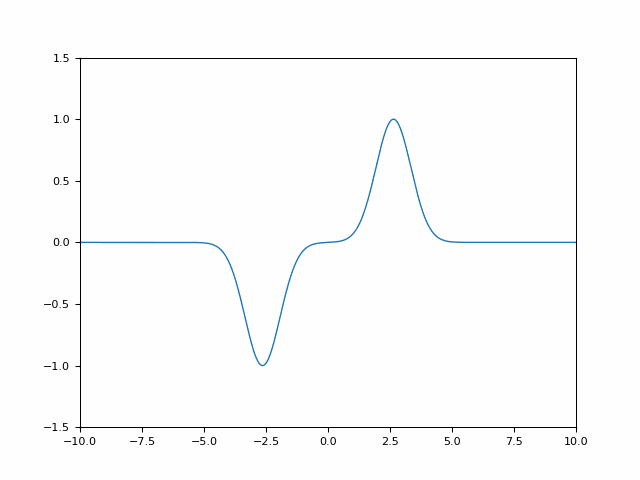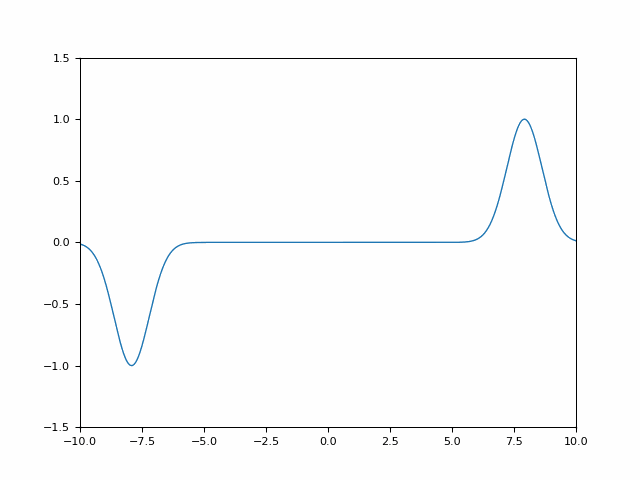
Eine Lösung mit vollständiger destruktiver Interferenz lautet
 = f(x-a+t) )
 = -f(x-t) )
 = \phi_{+,a}(x,t) + \phi_{-}(x,t) )
Es gilt
 = 0 )
D.h. das rechts sowie das links-laufende Wellenpaket löschen sich zu diesem Zeitpunkt gegenseitig exakt aus.
Energiedichte
Zur Berechnung der Energiedichte des Feldes verwenden wir die Lagrangedichte
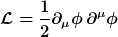
den daraus folgenden, kanonisch konjugierten Impuls
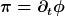
sowie die Hamiltondichte
^2 \right])
Letztere entspricht gerade der Energiedichte.
Die Erhaltung der Gesamtenergie zeigt man beispielsweise mittels
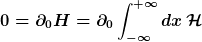
sowie im Folgenden der Anwendung der Wellengleichung, der Definition des Impulses sowie partieller Integration.
Anwendung auf die oben konstruierte Lösung
Für das Wellenpaket f sowie die Ableitung g = f‘ erhält man
 \pm g(x-t) )
^2 = g^2(x-a+t) + g^2(x-t) \pm \ldots)
Der gemischte Term fällt bei der Berechnung der Summe heraus, es bleibt
 + g^2(x-t))
(dass sich die Energiedichten der beiden Wellenplakete ohne Interferenzterm addieren, ist unserem Spezialfall, d.h. der Wahl von phi und f geschuldet)
Man beachte, dass die Energiedichte zu keinem Zeitpunkt – auch nicht bei vollständiger Auslöschung – verschwindet. Jedes einzelne Wellenpaket trägt immer konstante Energie, auch zum Zeitpunkt der Auslöschung! Die Energiedichte des Feldes steckt nicht in der Amplitude des Feldes, sondern in der zeitlichen sowie räumlichen Änderung derselben – das sind gerade die Ableitungen.
Der Zusammenhang mit dem Fall elektromagnetische Wellen
Man betrachtet zunächst die Energiedichte des elektromagnetischen Feldes
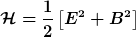
Dabei sind die elektrische und magnetische Felder in der gewählten Eichung
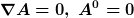
gegeben durch
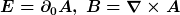
D.h., dem oben verwendeten Feld phi entspricht das Vektorpotential A, den elektrischen und magnetischen Feldern in etwa jeweils die jeweils erste Ableitung.
Beispiel
Recht überschaubar ist die Berechnung anhand der Funktion
 = e^{-\alpha x^2})
| Beschreibung: |
|
| Dateigröße: |
775.43 KB |
| Angeschaut: |
20750 mal |
|
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3403
|
| ML Verfasst am: 05. Apr 2023 22:50 Titel: Re: FAQ - Energieerhaltung im Fall destruktiver Interferenz |
|
|
Hallo,
| TomS hat Folgendes geschrieben: |
[...] Dazu betrachte ich zwei gegenläufig einlaufende Wellenpakete, die sich zu einem bestimmten Zeitpunkt gegenseitig auslöschen[...].
Man beachte, dass die Energiedichte zu keinem Zeitpunkt – auch nicht bei vollständiger Auslöschung – verschwindet. Jedes einzelne Wellenpaket trägt immer konstante Energie, auch zum Zeitpunkt der Auslöschung! Die Energiedichte des Feldes steckt nicht in der Amplitude des Feldes, sondern in der zeitlichen sowie räumlichen Änderung derselben – das sind gerade die Ableitungen. |
Ich denke, dass in dem Begriff der "vollständigen Auslöschung" eine Unschärfe steckt, die das Verständnis der Zusammenhänge erschwert.
In dem FAQ-Beitrag hast Du den Begriff der vollständigen Auslöschung in Bezug auf das Vektorpotential aufgefasst, was natürlich zulässig und nützlich ist. Man kann vollständige Auslöschung aber auch problemlos in Bezug auf das E-Feld oder das B-Feld verstehen. Das problematischste Verständnis liegt vermutlich vor, wenn man "vollständige Auslöschung" in Bezug auf die Energiedichte auffasst. Mit diesem Begriff im Kopf fällt es dann schwer zu verstehen, wohin bei Auslöschung die Energie geht.
Ich möchte im Folgenden den Begriff der vollständigen Auslöschung auf das E-Feld beziehen und zwei Wellenpakete mit einer in y-Richtung linear polarisierten elektromagnetischen betrachten, von denen sich die eine in die positive x-Richtung bewegt, während sich die andere in die negative x-Richtung bewegt.
Betrachten wir die Poyntingvektoren der beiden Wellen an einem beliebigen Punkt im Feld, so gilt für die beiden (voraussetzungsgemäß) entgegengesetzt gerichteten Komponenten:
)
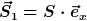
Da die Wellen in y-Richtung polarisiert sind und Auslöschung vorliegt, muss das E-Feld der einen Welle in die positive y-Richtung zeigen und die andere in die negative y-Richtung, also beispielsweise so:
)
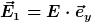
Es gilt dann: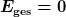 
Mithilfe der rechten Handregel erkennt man nun, dass sich das elektrische Feld zwar auslöscht, das magnetische Feld sich jedoch maximal konstruktiv überlagert:
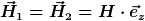
Es liegt dann alles andere als eine Auslöschung vor, da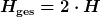 
In diesem Sinne geht dann die Aussage "Die Energie des Feldes steckt in der Amplitude" wieder auf.
Viele Grüße
Michael
PS: In der FAQ kann ich keine Bilder einfügen. Ist das Absicht?
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
