| Autor |
Nachricht |
Higgins
Anmeldungsdatum: 16.11.2006
Beiträge: 12
|
 Higgins Verfasst am: 16. Nov 2006 19:56 Titel: Freier Fall (Fallbeschleunigung?) |
 |
|
Hallo,
ich bin zur Zeit verwirrt. Hat die Masse eines Körpers etwas mit seiner Geschwindigkeit zu tun? Oder nur seine Form wegen dem Luftwiderstand?
Weil die Beschleunigung ist ja erstmal 9.81m/s² (Vakuum und hier auf der Erde auch, bloß wird sie durch den steigenden Luftwiderstand kleiner.
Heißt das alle Körper werden gleich stark angezogen bzw. beschleunigt und die Beschleunigung wir nur durch die unterschiedlich Oberflächenbeschaffenheit, die als Angriffsfläche für die Luft dient und aus der dann der Luftwiderstand resultiert, verringert?
Wir haben mal aufschrieben Tatsächliche Kraft=Gewichtskraft-Luftwiderstand, dass müsste nach meiner Vermutung aber doch falsch sein oder wie darf ich das verstehen?
Jetzt habe ich noch ein Beispiel:
Eine Eisen- und eine Styroporkugel haben den gleichen Radius und werden aus gleicher Höhe gleichzeitg fallen gelassen (KEIN VAKUUM). Wie verhalten sie sich? Wie kann man das begründen?
Folgende zwei Möglichkeiten sehe ich:
1. beide kommen gleichzeitig unten an, weil sie gleich stark angezogen werden und die gleiche Form haben und so dne gleichen Luftwiderstand erfahren
2. die Metallkugel landet zuerst, weil die Styroporkugel einen größeren Luftwiderstand erfährt, weil sie porös ist und so mehr Angriffsfläche vorhanden ist
Ich hoffe ihr könnt mir helfen.
Tschöö |
|
 |
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
| as_string Verfasst am: 16. Nov 2006 20:28 Titel: |
|
|
Hallo!
Ich glaube, dass Deine Probleme daraus entstehen, weil Du zu wenig zwischen Kraft und Beschleunigung unterscheidest.
Diese beiden hängen zwar eng zusammen, aber sind nicht identisch. Immerhin ist da ja noch die Masse als Faktor dazwischen.
Das mit der resultierenden Kraft ist schon so richtig. Allerdings musst Du diese noch durch die Masse teilen, um auf die Beschleunigung zu kommen.
Wenn Du keinen Luftwiderstand hast, dann ist ja die Kraft nur die Gewichtskraft, die höher ist, je größer die Masse ist. Um auf die Beschleunigung zu kommen musst Du aber wieder durch die Masse teilen und kommst so immer wieder zu der selben Beschleunigung, egal wie schwer der Körper wirklich ist.
Der Luftwiderstand hängt aber nicht von der Masse ab, sondern nur von der Geschwindigkeit und der Form des Körpers, auch von der Größe des Körpers (Angriffsfläche).
Wenn Du jetzt zwei gleich geformte Kugeln hast, dann haben die bei der gleichen Geschwindigkeit auch den selben Luftwiderstand.
Die Beschleunigung ist aber:
Die Beschleunigung hängt also noch von der Masse ab. Bei gleicher Form und ähnlicher Oberflächenbeschaffenheit hat man auch etwa den gleichen Luftwiderstand.
Gruß
Marco |
|
|
para
Moderator
Anmeldungsdatum: 02.10.2004
Beiträge: 2874
Wohnort: Dresden
|
| para Verfasst am: 16. Nov 2006 20:38 Titel: Re: Freier Fall (Fallbeschleunigung?) |
|
|
| Higgins hat Folgendes geschrieben: | | ich bin zur Zeit verwirrt. Hat die Masse eines Körpers etwas mit seiner Geschwindigkeit zu tun? Oder nur seine Form wegen dem Luftwiderstand? |
Okay, es scheint als würde hier etwas Verwirrung hinsichtlich einiger Begriffe herrschen. Dem soll natürlich Abhilfe geschaffen werden. ;-)
Das vielleicht am besten gleich vorweg: Die Masse eines Körpers ist eine feste Eigenschaft. Das heißt sie ist unabhängig von der Geschwindigkeit, vom Ort oder von anderen Einflüssen. (Alles in der klassischen Mechanik, in der Relativitätstheorie ist das leider nicht mehr so einfach.)
| Higgins hat Folgendes geschrieben: | Weil die Beschleunigung ist ja erstmal 9.81m/s² (Vakuum und hier auf der Erde auch, bloß wird sie durch den steigenden Luftwiderstand kleiner.
Heißt das alle Körper werden gleich stark angezogen bzw. beschleunigt und die Beschleunigung wir nur durch die unterschiedlich Oberflächenbeschaffenheit, die als Angriffsfläche für die Luft dient und aus der dann der Luftwiderstand resultiert, verringert? |
Richtig ist: alle Körper werden ihrer Masse entsprechend gleich stark angezogen. Daraus folgt aber nicht dass alle gleich stark beschleunigt werden. Die Kraft die ein Körper der Masse m im Abstand r vom Erdmittelpunkt durch die Erdanziehung erfährt kannst du mit dem Gravitationsgesetz berechnen:
Dabei ist Gamma die Gravitationskonstante und M_E die Erdmasse. Befindet man sich in der Nähe der Erdoberfläche, kann r als konstant und gleich dem Erdradius r_E angenommen werden. Dann kann man vereinfachend sagen:
Daraus ergibt sich der bekannte Wert für g. Warum heißt g jetzt aber Fallbeschleunigung? Nun, jeder Körper der Masse m wird von der Erde mit der Kraft F_g angezogen. Wirken keine anderen Kräfte auf ihn (handelt es sich also um einen freien Fall), wird er dadurch nach dem Newton'schen Axiom wie folgt beschleunigt:
Beim idealen freien Fall fallen also alle Körper unabhängig von ihrer Masse mit der gleichen Beschleunigung g, daher die Bezeichnung Fallbeschleunigung.
| Higgins hat Folgendes geschrieben: | | Wir haben mal aufschrieben Tatsächliche Kraft=Gewichtskraft-Luftwiderstand, dass müsste nach meiner Vermutung aber doch falsch sein oder wie darf ich das verstehen? |
Was oben steht gilt nur wenn die Gravitationskraft (also die Gewichtskraft) die einzige Kraft ist, die auf den Körper wirkt. Wirken noch weitere Kräfte, so addieren sich diese zur Gewichtskraft gemäß dem Prinzip der Kräfteaddition. Berücksichtigt man z.B. noch eine gewisse Reibungskraft die der Bewegung (und damit der Gewichtskraft) entgegengerichtet ist, erhält man:
Damit wird auch deutlich, warum ich gesagt habe, dass zwar alle Körper gleicher Masse gleich stark angezogen werden (die anziehende Kraft F_g ist von der Reibung ja absolut unabhängig), aber durch die zusätzliche Wirkung der Reibungskraft (die üblicherweise von Geschwindigkeit, Form und vielen anderen Faktoren des Körpers abhängt) werden bei weitem nicht alle Körper gleich stark beschleunigt. Das sieht man gut wenn man in der vorherigen Gleichung mal F durch diese Differenz ersetzt, womit sich die Masse des Körpers nicht mehr einfach rauskürzt.
| Higgins hat Folgendes geschrieben: | Jetzt habe ich noch ein Beispiel:
Eine Eisen- und eine Styroporkugel haben den gleichen Radius und werden aus gleicher Höhe gleichzeitg fallen gelassen (KEIN VAKUUM). Wie verhalten sie sich? Wie kann man das begründen? |
Das ist ein sehr gutes Beispiel um zu testen, inwiefern meine Erklärungen verständlich waren. Ich gebe noch einen Kommentar zu deinen zwei bisherigen Vorschlägen und du schreibst dann mal, ob du zu einem neuen Ergebnis gekommen bist, okay?
| Higgins hat Folgendes geschrieben: | 1. beide kommen gleichzeitig unten an, weil sie gleich stark angezogen werden und die gleiche Form haben und so dne gleichen Luftwiderstand erfahren
2. die Metallkugel landet zuerst, weil die Styroporkugel einen größeren Luftwiderstand erfährt, weil sie porös ist und so mehr Angriffsfläche vorhanden ist |
Es ist richtig anzunehmen, dass beide Kugeln (bei gleicher Geschwindigkeit) den gleichen Luftwiderstand erfahren. Deine Überlegung zur Oberflächenbeschaffenheit ist deshalb keineswegs falsch, aber vermutlich soll bei der Aufgabe auf solche Feinheiten nicht eingegangen werden. Die Reibungskraft ist also bei beiden Kugeln gleich groß wenn diese die gleiche Geschwindigkeit haben. Aber wie sieht es mit der Wirkung dieser Kräfte auf die jeweilige Beschleunigung der Kugeln aus? Kannst du einen Zusammenhang zur Gleichung (*) herstellen?
Ich hoffe dich damit nicht erschlagen zu haben. Wie gesagt: melde dich mal, inwiefern dir die Bemerkungen weitergeholfen haben.
//edit: Marco war schneller, dafür ist mein post auch länger ;-)
//edit2: quadrat korrigiert
_________________
Formeln mit LaTeX
Zuletzt bearbeitet von para am 16. Nov 2006 22:05, insgesamt einmal bearbeitet |
|
|
Higgins
Anmeldungsdatum: 16.11.2006
Beiträge: 12
|
| Higgins Verfasst am: 16. Nov 2006 21:52 Titel: |
|
|
Hallo,
okk ich glaube mir wird einiges klarer.
Kann ich also sagen, die Körper werden gleich stark angezogen, haben aber wegen verschiedenen Eigenschaften am Ende aber doch eine unterschiedliche Geschwindigkeit?
Am meisten verwirrt mich einfach, dass ich an verschiedenen Stellen was anderes lese. Im Physikbuch steht es so.. auf einer Internetseite steht die Masse ist unwichtig nach Galilei und wenn ich euch richtig verstanden habe, hat die Masse doch wieder was zusagen.
Bei meinem Beispiel würde ich dann doch eher zu 1. plädieren, bin mir aber unsicher.
Tschöö |
|
|
Rogowski
Anmeldungsdatum: 30.10.2006
Beiträge: 69
Wohnort: Linz / Austria
|
| Rogowski Verfasst am: 16. Nov 2006 22:17 Titel: |
|
|
| Higgins hat Folgendes geschrieben: | | Kann ich also sagen, die Körper werden gleich stark angezogen, haben aber wegen verschiedenen Eigenschaften am Ende aber doch eine unterschiedliche Geschwindigkeit? |
Du hast es erfasst. Es gibt da ein interessantes Experiment. Und zwar werden in einem zwei Vakuumzylindern eine Feder und ein Stein gleichzeitig losgelassen und man glaubt es kaum, sie treffen beide zur gleichen Zeit auf der Erde auf! |
|
|
pfnuesel
Anmeldungsdatum: 04.11.2004
Beiträge: 248
Wohnort: Zürich
|
| pfnuesel Verfasst am: 16. Nov 2006 22:26 Titel: |
|
|
Hallo
| Higgins hat Folgendes geschrieben: | | Kann ich also sagen, die Körper werden gleich stark angezogen, haben aber wegen verschiedenen Eigenschaften am Ende aber doch eine unterschiedliche Geschwindigkeit? |
Das kommt drauf an, was du unter "Anziehung" verstehst: Jeder Körper erfährt auf der Erde dieselbe Beschleunigung ( ), so gesehen ist deine Aussage richtig. Aber die Kraft (in diesem Fall: 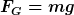 ) ist abhängig von der Masse des Körpers.
| Higgins hat Folgendes geschrieben: | | Am meisten verwirrt mich einfach, dass ich an verschiedenen Stellen was anderes lese. Im Physikbuch steht es so.. auf einer Internetseite steht die Masse ist unwichtig nach Galilei und wenn ich euch richtig verstanden habe, hat die Masse doch wieder was zusagen. |
Da steht überall dasselbe, nur musst du es richtig interpretieren. Für die Gewichtskraft, die auf der Erde herrscht, ist die Masse sehr wohl entscheidend. Eine Waage zeigt ja verschiedene Werte an, abhängig davon wie schwer die gewogene Person ist. Bei der Beschleunigung im Freien Fall gilt aber nach Newton:
Gehen wir davon aus, dass nur die Gravitationskraft der Erde wirkt (also kein Luftwiderstand!), dann wird das zu:
Die Masse kürzt sich also heraus und wir erhalten:
Das heisst: Jeder Körper, egal wie schwer, egal welche Form, wird im freien Fall mit 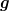 beschleunigt. Das ist, was Galilei dazumals herausgefunden hat.
Das lernt man auch zu Beginn weg in der Physik und trotzdem sieht man täglich, dass es nicht stimmt: Eine Bleikugel fällt viel schneller, als eine Feder. Da haben wir allerdings Luftwiderstand! Diesen haben wir in obiger Rechnung vernachlässigt. Aber beispielsweise auf dem Mond (oder in einem evakuierten Raum) würde die Feder genauso schnell zu Boden fallen, wie die Bleikugel. |
|
|
Higgins
Anmeldungsdatum: 16.11.2006
Beiträge: 12
|
| Higgins Verfasst am: 17. Nov 2006 16:36 Titel: |
|
|
Hallo,
muss man denn in diesem fall auch zwischen Gewichtskraft und der antreibenden Kraft unterscheiden? Ich würde sagen das wäre dann :
tatsächlich Kraft = Gewichtskraft-Luftwiderstand.
Also wie kann man das nochmal kurz zusammen fassen, welche Faktoren sind relevant?
Tschöö |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 17. Nov 2006 17:12 Titel: |
|
|
| Higgins hat Folgendes geschrieben: |
muss man denn in diesem fall auch zwischen Gewichtskraft und der antreibenden Kraft unterscheiden? Ich würde sagen das wäre dann :
tatsächlich Kraft = Gewichtskraft-Luftwiderstand.
|
Einverstanden  Damit hast du bereits einen der Ansatzpunkte verstanden, den du zum Lösen dieser Aufgabe brauchst. Aber ich finde, du hast noch einen großen Teil der Aufgabe vor dir.
Du hast dir nun überlegt, welche Kräfte wirken, und wie groß die Gesamtkraft ist.
Wie hängen nun diese Kräfte von der Masse ab?
Kannst du nun auch mit den Formeln, die du kennst, daraus folgern, wie groß die Beschleunigung ist?
------------------------------------------
Was für ein Ergebnis erhältst du, wenn du die Größe der Kräfte und die Größe der daraus folgenden Beschleunigung für die beiden verschiedenen Kugeln betrachtest und miteinander vergleichst?
Welche der Kräfte sind für die beiden Körper unterschiedlich groß, welche sind gleich groß?
(Du hast bereits richtig erkannt, dass die Luftwiderstandskraft für beide Kugeln gleich groß ist. Mit deiner Folgerung, dass das bedeutet, dass beide gleichzeitig unten ankommen, bin ich allerdings nicht einverstanden. Denn du hast ja selbst schon festgestellt, dass in der tatsächlichen Gesamtkraft auch noch die Gewichtskraft mit drinsteckt.)
Welche Anteile der Beschleunigung sind unterschiedlich groß. welche gleich groß? Für welchen der beiden Körper ist also die Gesamtbeschleunigung größer? |
|
|
Higgins
Anmeldungsdatum: 16.11.2006
Beiträge: 12
|
| Higgins Verfasst am: 17. Nov 2006 17:35 Titel: |
|
|
Also ...
Eisenkugel:
tatsächlich Krafat= Gewichtskrafta- Luftwiderstand
wegen der größeren Masse ist die Gewichtskraft größer und deshalb auch die tatsächliche Kraft
Syroporkugel:
tatsächlich Krafbt= Gewichtskraftb- Luftwiderstand
Fazit: Die Eisenkugel würde zuerst unten ankommen.
----
aber in meinem Physikbuch steht:
| Zitat: | | Das Bleikügelchen in der Fallröhre habe die 1000-fache masse der Flaumfeder. dann erfährt es auch eine 1000-mal so große Gewichtskraft. Es müsste also 100ß-mal so stark beschleunigt werden.1000fache Masse bedeutet aber auch 1000fache Trägheit. Schwere und Trägheit wirken einander genau entgegen, das Bleikügelchen fällt deshalb mit derselben Beschleunigung wie die Flaumfeder. |
Der im Zitat beschriebene Versuch läuft zwar im Vakuum ab und die Formen sind nicht gleich, aber der einzige Unterschied vom Vakuum zur normalen Umgebung ist, dass im Vakuum kein Luftwiderstand herrscht.
Also ist auch außerhalb normalerweise die Beschleunigung = 9-81m/s², bloß kommt da noch die bremsende Luft hinzu.
| Zitat: | | 1000-fache masse der Flaumfeder. dann erfährt es auch eine 1000-mal so große Gewichtskraft. Es müsste also 1000-mal so stark beschleunigt werden.1000fache Masse bedeutet aber auch 1000fache Trägheit. Schwere und Trägheit wirken einander genau entgegen, |
Aber wenn ich danach gehe ist, hängt die Beschleunigung doch wieder nciht von der Gewichtskraft ab oder habe ich schon wieder was falsch verstanden?
Tschöö |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 17. Nov 2006 17:50 Titel: |
|
|
Ich finde, mit dem, was du da zusammengestellt hast, bist du genau auf dem richtigen Weg (Wie du auf dein "Fazit" kommst, habe ich allerdings nicht verstanden, ich halte das an der Stelle für verfrüht: Um das wirklich beurteilen zu können, brauchst du glaube ich erst die Beschleunigungen.)
Um nun noch die Frage zu klären, ob deine Version gilt oder das aus dem Buch oder beides, solltest du nun bei der Beschleunigung genauer hinschauen.
Wie kannst du die Beschleunigung eines Körpers ausrechnen, wenn du die Kraft kennst, die auf ihn wirkt? Wie groß sind die Beschleunigungen der beiden Körper durch die Gewichtskräfte, und wie groß sind die Beschleunigungen der beiden Körper durch die Luftwiderstandskräfte? Welche Beschleunigungen sind gleich, welche unterschiedlich? Wie sieht also der Vergleich für die Gesamtbeschleunigungen aus? |
|
|
Higgins
Anmeldungsdatum: 16.11.2006
Beiträge: 12
|
| Higgins Verfasst am: 17. Nov 2006 19:06 Titel: |
|
|
Hallo,
F=m*a <=> a=F/m so kann ich die Beschleunigung ausrechnen. und F=m*g also ist a=g. Die beiden Beschleunigungen sind also gleich.
Für die Gewichtskräfte dürften sie unterschiedlich sein und für den Luftwiderstand gleich?
Richtig so? Also welche Version stimmt nun oder wie darf ich den Text aus meinem Buch verstehen?
Tschöö |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 17. Nov 2006 19:28 Titel: |
|
|
Überleg nochmal, anstatt zu vermuten und zu raten: Was ist denn jeweils das F und das m in deinen Formeln?
In welchem der Fälle, die du alle anschauen musst, handelt es sich um welche Kraft und welche Masse ? Wann meinst du die Gewichtskraft, wann die Luftwiderstandskraft, wann die Masse des schweren Körpers, wann die Masse des leichten Körpers?
Schreib mal für jede Formel und jeden betrachteten Fall dazu, welche Kraft und welche Masse du meinst. Magst du dazu die Gewichtskraft mit F_G, die Luftwiderstandskraft mit F_L, die schwere Masse mit m_1 und die leichte Masse mit m_2 bezeichnen? Und die Beschleunigung des schweren Körpers mit a_1 und die Beschleunigng des leichten Körpers mit a_2 ?
Für welche dieser Fälle erhältst du welche Folgerung? |
|
|
Higgins
Anmeldungsdatum: 16.11.2006
Beiträge: 12
|
| Higgins Verfasst am: 17. Nov 2006 19:42 Titel: |
|
|
Bist du sicher dass das so kompliziert richtig ist?
Also .
also
1. Eisen:
tatsächliche Kraft = F_G - F_L
F_G= m_1*a_1
=> tat. Kraft= (m_1*a_1)-F_L
und bei Styropor wäre es dann:
tatsächliche Kraft = F_G - F_L
F_G= m_2*a_2
=> tat. Kraft= (m_1*a_1)-F_L
F_L ist bei beiden gleich. Aber F_G ist bei beiden unterschiedlich?
Aber das bringt mich nicht weiter, mein Kopf sagt mir der Schwere ist zuerst unten, aber er sagt auch alles falsch.
So wie geht es nun weiter?
Tschöö |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 17. Nov 2006 19:48 Titel: |
|
|
| Higgins hat Folgendes geschrieben: |
und bei Styropor wäre es dann:
tatsächliche Kraft = F_G - F_L
F_G= m_2*a_2
=> tat. Kraft= (m_1*a_1)-F_L
|
Hier meinst du bestimmt in der letzten Zeile m_2 statt m_1.
Wie kannst du nun aus diesen Kräften die Beschleunigungen a_1 und a_2 ausrechnen? Was findest du heraus, wenn du diese beiden Beschleunigungen vergleichst? |
|
|
Higgins
Anmeldungsdatum: 16.11.2006
Beiträge: 12
|
| Higgins Verfasst am: 17. Nov 2006 19:54 Titel: |
|
|
Ja hast recht meine m_2 und a_2.
1. tat. Kraft= (m_1*a_1)-F_L => a= tat. Kraft/m
2. tat. Kraft= (m_2*a_2)-F_L => a= tat. Kraft/m
Die erste Kraft würde eine größere Beschleunigung zur Folge haben. Also würde das Eisen schneller fallen.
Falls die Aufgabe jetzt richtig gelöst ist, könntest du mir dann mal schreiben, wie du sie gelöst hättest und auf die Ausführung in meinem Physikbuch eingehen?
Tschöö |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 17. Nov 2006 19:57 Titel: |
|
|
| Higgins hat Folgendes geschrieben: | Ja hast recht meine m_2 und a_2.
1. tat. Kraft= (m_1*a_1)-F_L => a= tat. Kraft/m
2. tat. Kraft= (m_2*a_2)-F_L => a= tat. Kraft/m
|
Vergiss nicht, auch in dem, was du da folgerst, zu unterscheiden, um welche Beschleunigung und um welche Masse es sich jeweils handelt! Was meinst du oben mit dem m, und was unten mit dem m?
// edit:
Sorry, und einen Fehler hatte ich bisher ganz übersehen:
a_1 ist die gesamte Beschleunigung des ersten Körpers, nicht nur die Erdbeschleunigung g.
Also darfst du für die Gewichtskraft des ersten Körpers nicht
F_G,1 = m_1 * a_1
schreiben, sondern es muss heißen:
F_G,1 = m_1 * g
Das solltest du noch in deinen Gleichungen korrigieren, damit sie Sinn machen. |
|
|
Higgins
Anmeldungsdatum: 16.11.2006
Beiträge: 12
|
| Higgins Verfasst am: 17. Nov 2006 20:05 Titel: |
|
|
EDIT
1. tat. Kraft= (m_1*g)-F_L => a_1= tat. Kraft/m_1
2. tat. Kraft= (m_2*g)-F_L => a_2= tat. Kraft/m_2
Ergebnis würde ich sagen....hmm mal eben ein blatt nehmen....öhh ist weiterhin gleich, weiß irgendwie nicht wie ich das nun schriftlich überprüfen soll, wenn ich das ausflösen würde käme da ja raus:
-> a_1=F_1-F_L/m_1 also a_1=a_1-a_L
-> a_2=F_2-F_L/m_2 also a_2=a_2-a_L
dann könnte man das umstellen und gleichsetzen:
a_L=a_1-a_1
a_L=a_2-a_2 und das wars dann ne, also da hängt es
Falls die Aufgabe jetzt richtig gelöst ist, könntest du mir dann mal schreiben, wie du sie gelöst hättest und auf die Ausführung in meinem Physikbuch eingehen?
Tschöö |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 17. Nov 2006 20:26 Titel: |
|
|
| Higgins hat Folgendes geschrieben: |
-> a_1=F_1-F_L/m_1 also a_1=a_1-a_L
-> a_2=F_2-F_L/m_2 also a_2=a_2-a_L
|
Da ist noch einmal der Fehler mit dem a_1 bzw. a_2 statt dem g drin. Wenn du das korrigierst, bekommst du:
-> a_1=(F_G,1-F_L)/m_1 = g - (F_L/m_1) also a_1=g-a_L,1
-> a_2=(F_G,2-F_L)/m_2 = g - (F_L/m_2) also a_2=g-a_L,2
Kannst du nun die Beschleunigungen vergleichen? Wie sieht der Vergleich fr die beiden Beschleunigungen aus, die durch die Gravitationskraft verursacht werden? Wie sieht der Vergleich für die beiden Beschleunigungen a_L,1 und a_L,2 aus, die durch die Luftwiderstandskraft verursacht werden?
Welche Gesamtbeschleunigung ist also größer? Die des schweren oder die des leichten Körpers? Welcher Effekt sorgt hier also für den Unterschied in der Beschleunigung? |
|
|
Higgins
Anmeldungsdatum: 16.11.2006
Beiträge: 12
|
| Higgins Verfasst am: 17. Nov 2006 20:36 Titel: |
|
|
Den Fehler habe ich auch bemerkt, wollte dann aber nicht nochmal editieren weil du bestimmt schon am schreiben warst.
| Zitat: |
> a_1=(F_G,1-F_L)/m_1 = g - (F_L/m_1) also a_1=g-a_L,1
-> a_2=(F_G,2-F_L)/m_2 = g - (F_L/m_2) also a_2=g-a_L,2 |
Die Beschleunigungen durch die Gravitationskraft sind gleich.
bei der Luftwiderstandskraft würde ich sagen ist.
a_L,1 < a_L,2, weil m_1>m_2 und so nach der Division ein kleinerer Wert für a_L-1 rauskommt.
das heißt a_1 ist größer, weil g und g gleich, aber a_L,1 < a_L,2, .
Also fällt das Metall schneller.
Richtig`? Und wie kann man das nun in Worte fassen?
Kann man denn jetzt bei allen Körpern, auch mit unterschiedlicher Masse mit dieser Formel rechnen, man muss dann nur Luftwiderstand und so anpassen.
Und wie darf ich nun das in meinem Buch verstehen?
Danke schonmal, hat mich auf jeden Fall sehr viel weiter gebracht... wenn wir das alles durchhaben schreib ich hier noch ne kleine Zusammenfassung mit ein paar Ideen.
Tschöö |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 17. Nov 2006 20:55 Titel: |
|
|
| Higgins hat Folgendes geschrieben: |
| Zitat: |
> a_1=(F_G,1-F_L)/m_1 = g - (F_L/m_1) also a_1=g-a_L,1
-> a_2=(F_G,2-F_L)/m_2 = g - (F_L/m_2) also a_2=g-a_L,2 |
Die Beschleunigungen durch die Gravitationskraft sind gleich.
bei der Luftwiderstandskraft würde ich sagen ist.
a_L,1 < a_L,2, weil m_1>m_2 und so nach der Division ein kleinerer Wert für a_L-1 rauskommt.
das heißt a_1 ist größer, weil g und g gleich, aber a_L,1 < a_L,2, .
Also fällt das Metall schneller.
Richtig`? Und wie kann man das nun in Worte fassen?
|
Ganz genau
Wir haben also gesehen, dass bei gleich großer Luftwiderstandskraft der Körper mit der größeren Masse eine kleinere Bremsbeschleunigung erfährt. (Also wird der schwerere Körper weniger stark durch den Luftwiderstand gebremst und fällt dadurch schneller.)
| Zitat: |
Kann man denn jetzt bei allen Körpern, auch mit unterschiedlicher Masse mit dieser Formel rechnen, man muss dann nur Luftwiderstand und so anpassen.
|
Einverstanden
| Zitat: |
Und wie darf ich nun das in meinem Buch verstehen?
|
Das ist ganz genau dieselbe Überlegung wie die, die wir gerade vollzogen haben, nur dass in dem Fall aus dem Buch der Luftwiderstand Null ist. Dadurch wird die ganze Betrachtung ein bisschen einfacher und das Ergebnis für den Vergleich der Beschleunigungen ist ein anderes.
Schaffst du es, mit dem, was wir uns hier überlegt haben, durch denselben Weg, nur mit Weglassen des Luftwiderstandes, die Überlegung aus dem Buch nachzuvollziehen? |
|
|
Higgins
Anmeldungsdatum: 16.11.2006
Beiträge: 12
|
| Higgins Verfasst am: 17. Nov 2006 21:07 Titel: |
|
|
Also ich würde sagen:
F_Feder= m_Feder * g
F_MEtall= m_Metall * g
a_Feder= g = F_Feder/m_Feder
a_MEtall= g = F_Metall/m_Metall
---
Aber Fazit von allem ist doch eigentlich, dass die Gewichtskraft unwichtig ist und man nur die Masse beachten muss und halt die Form, richtig?
---
Hmm im Buch verwirrt mich nun Masse und Trägheit. Trägheit bedeutet ja, dass eine bestimmte Kraft aufgewandt werden muss um einen Körper zu bewegen. Und ist diese Kraft etwa so groß wie die Gewichtskraft, sodass wir F= F1 + (-F1) haben? F=0 null ist und dies dann für alle fällig gültig ist und man nur von a= g - aFl ausgehen muss?
Falls es dir jetzt anders vorkommt, dass was wir vorhin erarbeitet haben, habe ich verstanden. Nochmal Danke dafür.
Tschöö |
|
|
dermarkus
Administrator
Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
| dermarkus Verfasst am: 17. Nov 2006 21:31 Titel: |
|
|
Einverstanden
| Higgins hat Folgendes geschrieben: |
Aber Fazit von allem ist doch eigentlich, dass die Gewichtskraft unwichtig ist und man nur die Masse beachten muss und halt die Form, richtig?
|
Sag das nicht, wenn die Gewichtskraft in der Nähe ist, sonst ist sie am Ende beleidigt 
Einverstanden, für den Vergleich der Beschleunigungen zweier fallender Körper bewirkt die Gewichtskraft keinen Unterschied. Die Luftwiderstandskraft ist es, die dafür sorgt, dass die Beschleunigung zweier Körper, je nach deren Form und Masse, unterschiedlich sein kann.
---------
Die Formulierung aus dem Buch
| Zitat: |
Schwere und Trägheit wirken einander genau entgegen
|
halte ich hier für ein bisschen abstrakt und deshalb möglicherweise verwirrend.
Schwere und Trägheit würde ich als zwei Eigenschaften der Masse erklären:
Die schwere Masse bestimmt, wie stark die Gewichtskraft ist, die an dem Körper zieht:
Die träge Masse bestimmt, wie stark sich ein Körper dagegen wehrt, von einer an ihm angreifenden Kraft beschleunigt zu werden:
Die träge Masse eines Körpers ist gleich groß wie seine schwere Masse. Wenn die Gewichtskraft genau die Gesamtkraft ist, die den Körper beschleunigt, dann wird also der Körper immer genau mit der Beschleunigung a=g beschleunigt.
Das Buch will also, für den Fall ohne Luftwiderstand, einfach nur sagen: Wenn ein Körper eine größere Masse hat, dann wirkt auf ihn eine größere Gewichtskraft, also eine größere beschleunigende Kraft nach unten. Weil seine Masse größer ist, ist er aber gleichzeitig auch träger, also schwieriger zu beschleunigen, und zwar genau so viel träger, dass seine Beschleunigung genauso groß ist wie die Beschleunigung eines leichteren Körpers.
Oder etwas flapsiger: Je schwerer, desto träge, also bleibt die Fallbeschleunigung für jede Masse gleich |
|
|
Higgins
Anmeldungsdatum: 16.11.2006
Beiträge: 12
|
| Higgins Verfasst am: 18. Nov 2006 22:53 Titel: |
|
|
So dann will ich das abschließend nochmal zusammenfassen....
Ja eigentlich gibt es da nur folgendes zu sagen: Die Beschleunigung ist von der Gewichtskraft unabhängig nur vom Luftwiderstand und der Masse abhängig. Im Vakuum ist sie von beidem unabhängig.
Danke nochmal an euch und besonders an "dermarkus". 
Mal gucken wie dann die Arbeit am Montag wird.
Tschöö |
|
|
|
|
Registrieren
Login
FAQ
Suchen
