| Autor |
Nachricht |
antaris
Anmeldungsdatum: 12.12.2022
Beiträge: 477
Wohnort: In einem chaotischen Universum
|
 antaris Verfasst am: 16. Feb 2024 14:56 Titel: Diskussion: FAQ - Zeitdilatation, Längenkontraktion, lin.... |
 |
|
Diskussion zum Thread FAQ - Zeitdilatation, Längenkontraktion, lineare Algebra
@TomS
Danke für die Arbeit.
Du hast den Thread gesperrt. So kann man nicht zitieren und dann das geschriebene kopieren.
Eins nach dem anderen:
Beitrag 1: Zeidilatation
Verstanden: wenn die Weltlinie C geradlinig ist, dann ist tau = t,weil keine Lorentztransformation besteht. Da x=0 und damit v=xt=0 findet die Bewegung nur in der Koordinate t statt.
Verstanden: wenn die Weltlinie C krummlinig ist, dann ist tau * gamma = t.
Die Eigenzeit tau ist in beiden Fällen die invariante Größe.
Gamma ist in Abhängigkeit von der Relativgeschwindigkeit. Je größer die Geschwindigkeit, desto kleiner wird t. Ich vergleiche das mit einem Festwiderstand (unter nicht Beachtung von Temperaturunterschiede). Der Widerstand ist invariant und wenn ich Spannung oder Strom ändere, so ändert sich immer die andere Größe mit. Nur der Widerstand hat immer den gleichen Wert.
Was ich eben nicht verstanden habe ist der Formalismus. Man könnte das alles auch mit "normalen Gleichungen" wie man sie aus der Schulzeit kennt genauso schreiben, wie mit dem Formalismus. Der Formalismus verkürzt aber die Schreibweise und macht es übersichtlicher...einen sonstigen Unterschied gibt es nicht?
Mit "normale Gleichungen" meine ich z.B. das bei Wiki zur Eigenzeit:
https://de.wikipedia.org/wiki/Zeitdilatation#Eigenzeit
| Zitat: | | Interessant ist, dass ich zur Berechnung nie das Ruhesystem des mit v bewegten Beobachters genutzt habe; die Berechnung von tau ist in jedem beliebigen Koordinatensystem möglich. Der Witz dabei ist wie gesagt, dass wir Koordinate t und Eigenzeit tau unterscheiden; t transformiert sich unter Lorentz-Transformation (die wir hier für t und x nicht betrachtet haben) tau ist dagegen invariant (Beweis kann ich nachliefern). |
Bei der Berechnung muss man ja auch gar nicht das Ruhesystem des mit v bewegten Beobachters genutzt werden. Man kann einfach wechseln, denn lokal tickt jede Uhr gleich. Wenn tau invariant ist, dann bei allen Beobachtern und egal wie diese relativ zueinander bewegt sind.
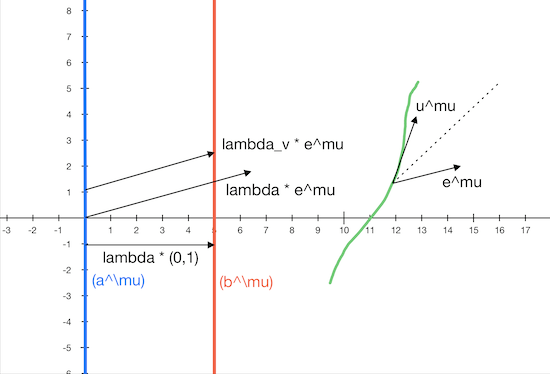
Ich habe bei dem Bild auch nur die Betrachtung aus einem Ruhesystem gemacht. Dem was in unendlicher Entfernung zur Masse in Ruhe steht bzw. in dem verschwindend die Gravitation der Masse wirkt.
Daraus ergibt sich eine von außen nach innen zunehmende Zeitdilatation (und Längenkontraktion), je kleiner der Radius zur Masse wird....oder nicht?
|
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18081
|
| TomS Verfasst am: 16. Feb 2024 16:34 Titel: Re: Diskussion: FAQ - Zeitdilatation, Längenkontraktion, lin |
|
|
| antaris hat Folgendes geschrieben: | Beitrag 1: Zeidilatation
Verstanden: wenn die Weltlinie C geradlinig ist, dann ist tau = t,weil keine Lorentztransformation besteht. Da x=0 und damit v=xt=0 findet die Bewegung nur in der Koordinate t statt.
Verstanden: wenn die Weltlinie C krummlinig ist, dann ist tau * gamma = t.
Die Eigenzeit tau ist in beiden Fällen die invariante Größe. |
Es ist doch hoffentlich verständlich, dass ich gar keine Lorentz-Transformation nutze.
Und krummlinig ist da gar nichts. Wir reden von Geraden im Sinne von
 = vt)
in einer flachen Raumzeit der SRT.
| antaris hat Folgendes geschrieben: | | Gamma ist in Abhängigkeit von der Relativgeschwindigkeit. Je größer die Geschwindigkeit, desto kleiner wird t. Ich vergleiche das mit einem Festwiderstand … |
Das trägt nicht zum geometrischen Verständnis bei.
| antaris hat Folgendes geschrieben: | Was ich eben nicht verstanden habe ist der Formalismus. Man könnte das alles auch mit "normalen Gleichungen" wie man sie aus der Schulzeit kennt genauso schreiben, wie mit dem Formalismus. Der Formalismus verkürzt aber die Schreibweise und macht es übersichtlicher...einen sonstigen Unterschied gibt es nicht?
Mit "normale Gleichungen" meine ich z.B. das bei Wiki zur Eigenzeit:
https://de.wikipedia.org/wiki/Zeitdilatation#Eigenzeit |
Ja, natürlich sind diese Formalismen äquivalent.
Mit war jedoch wichtig, dass die invarianten Messgrößen tau und lambda anders behandelt werden und anders in die Gleichungen eingehen als die Koordinaten t und x. Das sieht man im Falle der Geradengleichung explizit.
| antaris hat Folgendes geschrieben: | | Zitat: | | Interessant ist, dass ich zur Berechnung nie das Ruhesystem des mit v bewegten Beobachters genutzt habe; die Berechnung von tau ist in jedem beliebigen Koordinatensystem möglich. Der Witz dabei ist wie gesagt, dass wir Koordinate t und Eigenzeit tau unterscheiden; t transformiert sich unter Lorentz-Transformation (die wir hier für t und x nicht betrachtet haben) tau ist dagegen invariant (Beweis kann ich nachliefern). |
Bei der Berechnung muss man ja auch gar nicht das Ruhesystem des mit v bewegten Beobachters genutzt werden. Man kann einfach wechseln, denn lokal tickt jede Uhr gleich. Wenn tau invariant ist, dann bei allen Beobachtern und egal wie diese relativ zueinander bewegt sind. |
Was du hier so gelassen aussprichst, ist ja schon eine tiefere Einsicht.
Häufig wird die Lorentz-Kontraktion sowie die Zeitdilatation mittels Lorentz-Transformation zwischen Koordinaten "hergeleitet". Der Punkt ist, dass diese Koordinaten für sich betrachtet überhaupt keine physikalische Bedeutung haben, sondern zunächst reine Rechengrößen darstellen. Um ihnen nun eine physikalische Bedeutung zukommen zu lassen, identifiziert man den Wechsel zwischen den Koordinatensystemen mit dem Wechsel zwischen Beobachtern, und man identifiziert Lorentz-Kontraktion und Zeitdilatation mit Verhältnissen von Koordinaten zweier verschiedener Koordinatensysteme. Und das ist – aus vielerlei Gründen – Quatsch.
Insbs. versteht man nicht, dass die gemessenen Größen Lorentz-invariante Größen sind.
Wie gesagt, mit war wichtig, dass die invarianten Messgrößen tau und lambda anders behandelt werden und eine andere Bedeutung haben als die Koordinaten t und x.
Und mir war wichtig, – siehe letzter Beitrag im FAQ – dass der Wechsel zwischen Koordinatensystemen und der Wechsel zwischen Beobachtern sowohl physikalisch als auch mathematisch etwas völlig anderes ist.
Wenn das nicht klar wird, muss ich es nochmal herausstellen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18081
|
| TomS Verfasst am: 16. Feb 2024 16:39 Titel: Re: Diskussion: FAQ - Zeitdilatation, Längenkontraktion, lin |
|
|
| antaris hat Folgendes geschrieben: | | Ich habe bei dem Bild… |
Ich fürchte, das führt hier zu nichts. Das Bild erinnert an die vereinfachte Darstellung einer gekrümmten Raumzeit – besser gesagt, eines gekrümmten Raumes. Das hat nun aber mit Zeitdilatation und Längenkontraktion sowie Ruhesystemen – wie wir es hier diskutieren – nichts zu tun.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Phoros
Anmeldungsdatum: 08.02.2024
Beiträge: 13
|
| Phoros Verfasst am: 16. Feb 2024 16:58 Titel: Re: Diskussion: FAQ - Zeitdilatation, Längenkontraktion, lin |
|
|
| Zitat: | | Wenn das nicht klar wird, muss ich es nochmal herausstellen. |
Das wäre gut. Repräsentiert ein Koordinatensystem nicht einen Beobachter?
|
|
|
MBastieK
Anmeldungsdatum: 06.10.2012
Beiträge: 951
Wohnort: Berlin-Wedding
|
| MBastieK Verfasst am: 16. Feb 2024 17:03 Titel: Re: Diskussion: FAQ - Zeitdilatation, Längenkontraktion, lin |
|
|
| Phoros hat Folgendes geschrieben: | | Repräsentiert ein Koordinatensystem nicht einen Beobachter? |
Habe ich mich auch gefragt.
Nette Grüsse
_________________
Intelligenz ist die Fähigkeit der (temporären) Anpassung. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18081
|
| TomS Verfasst am: 16. Feb 2024 17:15 Titel: |
|
|
Das ist in der speziellen Relativitätstheorie normalerweise möglich, jedoch aus verschiedenen Gründen nicht unproblematisch; es sollte näher diskutiert werden.
Die SRT wird fast ausschließlich in Inertialsystemen formuliert. Identifiziert man nun Koordinatensysteme immer mit Beobachtern, so gelangt man unmittelbar zum Schluss, dass eine beschleunigte Bewegung bzw. beschleunigte Beobachter im Rahmen der SRT nicht diskutiert werden können, sondern dass dazu die ART notwendig sei – falsch!
Identifiziert man Beobachter und Koordinatensysteme, so wird nicht klar, was es mit relativen bzw. invarianten Größen genau auf sich hat. Viele Größen sind eben relativ zu einem bestimmten Beobachter definiert, jedoch invariant unter Koordinatentransformationen. Um das zu verstehen, muss man eine Identifizierung von Beobachter und Koordinatensysteme vermeiden. Im FAQ-Beitrag diskutiere ich insbesondere, dass die Eigenzeit eines Beobachters invariant unter Koordinatentransformationen ist, jedoch natürlich nicht unter Beobachterwechsel – ein anderer Beobachter misst logischerweise eine andere Eigenzeit. Dies erkennt man in einer geeigneten Darstellung bereits daran, dass eine andere mathematische Größe vorliegt. Siehe im FAQ auch das Beispiel aus der Newtonschen Mechanik.
Bei der Auflösung des Zwillingsparadoxon wird häufig darauf verwiesen, dass der auf der Erde zurückgebliebene Zwilling sich immer in dem selben in Arial System befindet, während der Reisende am Umkehr das Initials System wechselt. Zwar ist dies richtig, jedoch für die Erklärung des Zwilling Paradoxon völlig belanglos, da in einer geeigneten Berechnung überhaupt kein Beobachter, kein Bezugssystem eines der beiden Beobachter verwendet werden muss. Schlimmer noch – versteift man sich auf die Erklärung mittels inner Aals Systemen, so wird es unmöglich, vernünftig über die Zeitdilatation zwischen zwei Reisenden zu sprechen, die sich beide beschleunigt und somit niemals in einem Ingalls System bewegen.
EDIT: Ein Koordinatensystem schreibt jedem Punkt bzw. jedem Ereignis in der Raumzeit eineindeutig ein Tupel aus vier Koordinaten zu, eine Zeit- und drei Ortskoordinaten. Ein Beobachter ist ein reales oder hypothetisches Objekt, dass sich entlang einer Weltlinie durch die Raumzeit bewegt; es existiert zu jedem Moment seiner Eigenzeit nur an genau einem Ort auf dieser Weltlinie, und insbesondere nie in der gesamten Raumzeit. Die Verwendung des lokal beim Beobachter gültigen Koordinatensystems – zum Beispiel im Inneren seiner Raumkapsel – zu einem für die gesamte Raumzeit global gültigen Koordinatensystem ist offensichtlich eine theoretische Extrapolation. Ein Beobachter ist daher sicher nicht mit einem Koordinatensystem identisch, er kann jedoch gegebenenfalls sein lokales Koordinatensystem zu einer Konstruktion eines globalen Koordinatensystems nutzen (dies schlägt jedoch fehl für nicht-inertial bewegte Beobachter; ihr lokales Koordinatensystem gilt üblicherweise nicht für die gesamte Raumzeit sondern enthält Horizonte, jenseits derer es nicht fortsetzbar ist).
Das alles bedeutet nicht, dass es nicht möglich ist, ausgehend von einem geeigneten Beobachter ein geeignetes Koordinatensystem zu definieren.
Mein Lieblingsbeispiel ist die relativistische Dopplerverschiebung, d.h. die von einem Beobachter mit Vierergeschwindigkeit u gemessene Frequenz omega einer Lichtwelle bzw. eines Photons mit Wellen- bzw. Viererimpulsvektor k:
0) Der Beobachter misst die Frequenz
 = (u, k))
Wobei der Klammerausdruck für das Skalarprodukt der beiden Vierervektoren steht.
1) Ein anderer Beobachter
misst eine andere Frequenz
 = (\bar{u}, k))
2) Der erste Beobachter misst jedoch die selbe Frequenz, auch wenn man die Berechnung dieser Frequenz im Bezugsystem des zweiten Beobachters durchführt:
 = (\bar{u}, \bar{k}) = (u, k) = \omega_u(k))
Das Skalarprodukt ist invariant unter Lorentz-Transformation d.h. unter Wechsel des Koordinatensystems, jedoch nicht unter Wechsel des Beobachters.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 16. Feb 2024 18:26, insgesamt 7-mal bearbeitet |
|
|
Phoros
Anmeldungsdatum: 08.02.2024
Beiträge: 13
|
| Phoros Verfasst am: 16. Feb 2024 17:38 Titel: |
|
|
Ist mir nicht klar geworden.
Wie werden "Beobachter" & "KS" definiert? Kann man hieran was erkennen?
|
|
|
antaris
Anmeldungsdatum: 12.12.2022
Beiträge: 477
Wohnort: In einem chaotischen Universum
|
| antaris Verfasst am: 16. Feb 2024 17:57 Titel: Re: Diskussion: FAQ - Zeitdilatation, Längenkontraktion, lin |
|
|
| TomS hat Folgendes geschrieben: | | antaris hat Folgendes geschrieben: | Beitrag 1: Zeidilatation
Verstanden: wenn die Weltlinie C geradlinig ist, dann ist tau = t,weil keine Lorentztransformation besteht. Da x=0 und damit v=xt=0 findet die Bewegung nur in der Koordinate t statt.
Verstanden: wenn die Weltlinie C krummlinig ist, dann ist tau * gamma = t.
Die Eigenzeit tau ist in beiden Fällen die invariante Größe. |
Es ist doch hoffentlich verständlich, dass ich gar keine Lorentz-Transformation nutze.
Und krummlinig ist da gar nichts. Wir reden von Geraden im Sinne von
in einer flachen Raumzeit der SRT. |
Die Raumzeit im Abstand zweier Ereignisse mit einer Relativgeschwindigkeit zueinander, krümmt sich nicht Aufgrund der Zeitdilatation? Weil die SRT nur bei infinitesimalen Abständen gültig ist und somit in Näherung lokal flach?
| TomS hat Folgendes geschrieben: | | antaris hat Folgendes geschrieben: | | Gamma ist in Abhängigkeit von der Relativgeschwindigkeit. Je größer die Geschwindigkeit, desto kleiner wird t. Ich vergleiche das mit einem Festwiderstand … |
Das trägt nicht zum geometrischen Verständnis bei. |
Aber das ist doch genau das geometrische Bild, was man mit dem Minkowski-Diagramm so schön veranschaulichen kann.
| TomS hat Folgendes geschrieben: | | antaris hat Folgendes geschrieben: | Was ich eben nicht verstanden habe ist der Formalismus. Man könnte das alles auch mit "normalen Gleichungen" wie man sie aus der Schulzeit kennt genauso schreiben, wie mit dem Formalismus. Der Formalismus verkürzt aber die Schreibweise und macht es übersichtlicher...einen sonstigen Unterschied gibt es nicht?
Mit "normale Gleichungen" meine ich z.B. das bei Wiki zur Eigenzeit:
https://de.wikipedia.org/wiki/Zeitdilatation#Eigenzeit |
Ja, natürlich sind diese Formalismen äquivalent. |
Ok, dann würde mir eine Übersetzung "kurzer Formalisums = langer Formalismus" helfen das besser zu verstehen.
| TomS hat Folgendes geschrieben: | | Mit war jedoch wichtig, dass die invarianten Messgrößen tau und lambda anders behandelt werden und anders in die Gleichungen eingehen als die Koordinaten t und x. Das sieht man im Falle der Geradengleichung explizit. |
Ich denke genau das auch verstanden zu haben.
| TomS hat Folgendes geschrieben: | | antaris hat Folgendes geschrieben: | | Zitat: | | Interessant ist, dass ich zur Berechnung nie das Ruhesystem des mit v bewegten Beobachters genutzt habe; die Berechnung von tau ist in jedem beliebigen Koordinatensystem möglich. Der Witz dabei ist wie gesagt, dass wir Koordinate t und Eigenzeit tau unterscheiden; t transformiert sich unter Lorentz-Transformation (die wir hier für t und x nicht betrachtet haben) tau ist dagegen invariant (Beweis kann ich nachliefern). |
Bei der Berechnung muss man ja auch gar nicht das Ruhesystem des mit v bewegten Beobachters genutzt werden. Man kann einfach wechseln, denn lokal tickt jede Uhr gleich. Wenn tau invariant ist, dann bei allen Beobachtern und egal wie diese relativ zueinander bewegt sind. |
Was du hier so gelassen aussprichst, ist ja schon eine tiefere Einsicht. |
Diese Einsicht hatte ich schon vor längerer Zeit.
| TomS hat Folgendes geschrieben: | | Häufig wird die Lorentz-Kontraktion sowie die Zeitdilatation mittels Lorentz-Transformation zwischen Koordinaten "hergeleitet". Der Punkt ist, dass diese Koordinaten für sich betrachtet überhaupt keine physikalische Bedeutung haben, sondern zunächst reine Rechengrößen darstellen. Um ihnen nun eine physikalische Bedeutung zukommen zu lassen, identifiziert man den Wechsel zwischen den Koordinatensystemen mit dem Wechsel zwischen Beobachtern, und man identifiziert Lorentz-Kontraktion und Zeitdilatation mit Verhältnissen von Koordinaten zweier verschiedener Koordinatensysteme. Und das ist – aus vielerlei Gründen – Quatsch. |
Ich weiß nicht. Beobachter bestehen aus Materie die Masse hat. Darum geht es. Wie verhalten sich verschieden massereiche und verschieden relativ bewegte Massen=Beobachter zueinander und wie wirken sie auf die Raumzeit.
| TomS hat Folgendes geschrieben: | | Insbs. versteht man nicht, dass die gemessenen Größen Lorentz-invariante Größen sind. |
Wenn wir das Myon auf der Erde Messen, dann doch nur aufgrund durch die Zeitdilatation der Koordinatenzeit t, bei der hoher Geschwindigkeit. Kann man die Eigenzeit eines solchen Myons direkt messen?
| TomS hat Folgendes geschrieben: | Und mir war wichtig, – siehe letzter Beitrag im FAQ – dass der Wechsel zwischen Koordinatensystemen und der Wechsel zwischen Beobachtern sowohl physikalisch als auch mathematisch etwas völlig anderes ist.
Wenn das nicht klar wird, muss ich es nochmal herausstellen. |
Ja aber dazu muss man wissen was ko- bzw. kontravariant bedeutet. Diesen Unterschied gerne besser herausstellen.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18081
|
| TomS Verfasst am: 16. Feb 2024 18:00 Titel: |
|
|
| Phoros hat Folgendes geschrieben: | | Ist mir nicht klar geworden. |
Schau dir den Beitrag nochmal an; habe ihm ergänzt.
| Phoros hat Folgendes geschrieben: | | Wie werden "Beobachter" & "KS" definiert? Kann man hieran was erkennen? |
Ein Koordinatensystem ist ganz genauso wie in drei Dimensionen die eineindeutige Zuschreibung von Koordinaten-Tupeln zu Punkten bzw. Ereignissen in der Raumzeit.
Z.B. heute Mittag in Greenwich: (16.02.2024 12:00:00, 0, 51.48, 6365 km)
Ein Beobachter hat zu jedem Zeitpunkt einen bestimmten Ort, d.h. er folgt einer Weltlinie C durch die 4-dim. Raumzeit, beschrieben durch einen Vierervektor x. Der tangentiale Einheitsvektor an die Weltlinie ist die so genannte Vierergeschwindigkeit des Beobachters u. Diese entspricht genau der Ableitung des Vierervektors x nach der Eigenzeit tau entlang der Weltlinie C:
Das Koordinatensystem ist global für die vierdimensionale Raumzeit definiert, der Beobachter, seinen Ort, seine Geschwindigkeit und seine Eigenzeit nur entlang der Weltlinie.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 16. Feb 2024 18:10, insgesamt 3-mal bearbeitet |
|
|
antaris
Anmeldungsdatum: 12.12.2022
Beiträge: 477
Wohnort: In einem chaotischen Universum
|
| antaris Verfasst am: 16. Feb 2024 18:06 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Identifiziert man Beobachter und Koordinatensysteme, so wird nicht klar, was es mit relativen bzw. invarianten Größen genau auf sich hat. Viele Größen sind eben relativ zu einem bestimmten Beobachter definiert, jedoch invariant unter Koordinatentransformationen. Um das zu verstehen, muss man eine Identifizierung von Beobachter und Koordinatensysteme vermeiden. Im FAQ-Beitrag diskutiere ich insbesondere, dass die Eigenzeit eines Beobachters invariant unter Koordinatentransformationen ist, jedoch natürlich nicht unter Beobachterwechsel – ein anderer Beobachter misst logischerweise eine andere Eigenzeit. Dies erkennt man in einer geeigneten Darstellung bereits daran, dass eine andere mathematische Größe vorliegt. Siehe im FAQ auch das Beispiel aus der Newtonschen Mechanik. |
Also geht es darum, dass Vektoren bei einer Koordinatentransformation die gleiche physikalische Bedeutung haben müssen? Die Koordinatentransformation entspricht einer Abbildung wie z.B. Translation, Rotation usw.?
Dann besteht der Unterschied darin, dass der Beobachter ein Ereignis aus einem bestimmten Abstand beobachtet und bei Koordinatentrnsformation ein Ereignis von einer Raumzeit in eine andere hineintransformiert wird und sich dabei selbst nicht verändert (anstelle dessen ändert sich die Umgebung)?
Wenn ich also am Ereignis mehr als weniger direkt vorbeifliege, dann messe ich die gleiche Zeit/Länge, wie ein am Ereignis ruhender Beobachter...weil sich das Ereignis und ich zu diesem Zeitpunkt annähernd in der "gleichen Raumzeit" befinden? Das meinst du mit 2 Geraden treffen sich auf der Ebene?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18081
|
| TomS Verfasst am: 16. Feb 2024 18:14 Titel: |
|
|
| antaris hat Folgendes geschrieben: | | Also geht es darum, dass Vektoren bei einer Koordinatentransformation die gleiche physikalische Bedeutung haben müssen? |
Ja.
| antaris hat Folgendes geschrieben: | | Die Koordinatentransformation entspricht einer Abbildung wie z.B. Translation, Rotation usw.? |
Ja.
| antaris hat Folgendes geschrieben: | | Dann besteht der Unterschied darin, dass der Beobachter ein Ereignis aus einem bestimmten Abstand beobachtet und bei Koordinatentrnsformation ein Ereignis von einer Raumzeit in eine andere hineintransformiert wird? |
Bei den meisten Berechnungen wird implizit vorausgesetzt, dass die Beobachtung lokal erfolgt, d.h. man berücksichtigt im Allgemeinen nicht, dass sich zunächst ein Lichtstrahl vom Ereignis zum Beobachter ausbreiten muss. Das ist ein weiterer Punkt, den ich oben ich ergänze.
Nein, die Koordinatentransformation transformiert nicht zwischen zwei verschiedenen Raumzeiten, sondern zwischen zwei Koordinatensystemen für die selbe Raumzeit. Durch die Einführung verschiedener Weltkarten in Atlanten erzeugt du auch keine neuen Erden.
| antaris hat Folgendes geschrieben: | | Wenn ich also am Ereignis mehr oder weniger direkt vorbeifliege, dann messe ich die gleiche Länge, wie ein am Objekt ruhender Beobachter...weil sich das Ereignis und ich zu diesem Zeitpunkt annähernd in der "gleichen Raumzeit" befinden? |
Ich verstehe nicht genau, was du messen willst, aber ich fürchte, die Antwort lautet Nein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Phoros
Anmeldungsdatum: 08.02.2024
Beiträge: 13
|
| Phoros Verfasst am: 16. Feb 2024 18:21 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Das Koordinatensystem ist global für die vierdimensionale Raumzeit definiert, der Beobachter, seinen Ort, seine Geschwindigkeit und seine Eigenzeit nur entlang der Weltlinie. |
Es wird klarer. Kann man nicht an jeden Beobachter ein KS hängen? Das würde den Beobachter aber auch nicht "objektivieren", oder?
In welchem Fallbeispiel wäre die identische Verwendung zweifelhaft?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18081
|
| TomS Verfasst am: 16. Feb 2024 18:39 Titel: Re: Diskussion: FAQ - Zeitdilatation, Längenkontraktion, lin |
|
|
| antaris hat Folgendes geschrieben: | | Die Raumzeit im Abstand zweier Ereignisse mit einer Relativgeschwindigkeit zueinander, krümmt sich nicht Aufgrund der Zeitdilatation? |
Nee, da krümmt sich nichts.
| antaris hat Folgendes geschrieben: | | Aber das ist doch genau das geometrische Bild, was man mit dem Minkowski-Diagramm so schön veranschaulichen kann. |
Schlimmstenfalls hast du sie falsch verstanden.
Sie veranschaulichen Koordinaten,achsen, Welt,linien von Beobachtern, Lichtstrahlen … Die quantitative Berechnung bzw. das Messen von Abständen ist jedoch nicht unmittelbar einsichtig.
| antaris hat Folgendes geschrieben: | | Ok, dann würde mir eine Übersetzung "kurzer Formalisums = langer Formalismus" helfen das besser zu verstehen. |
Können wir machen.
| antaris hat Folgendes geschrieben: | | Ich weiß nicht. Beobachter bestehen aus Materie die Masse hat. |
Wie so oft verwendet man natürlich idealisierte Beobachter, die so klein und massearm sind, dass sie nie auf die Raumzeit wirken; sicher nicht in der SRT, denn da ist die Raumzeit starr, jedoch auch nicht in der ART.
| antaris hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Insbs. versteht man nicht, dass die gemessenen Größen Lorentz-invariante Größen sind. |
Wenn wir das Myon auf der Erde Messen, dann doch nur aufgrund durch die Zeitdilatation der Koordinatenzeit t, bei der hoher Geschwindigkeit. Kann man die Eigenzeit eines solchen Myons direkt messen? |
Na, man müsste sozusagen neben her fliegen.
Was man an Beschleunigern tatsächlich messen kann, ist zum einen der Zerfall von im Speicherring kreisenden Elementarteilchen bzw. deren Zerfallsprodukte, zum anderen die Anzahl der Elementarteilchen im Speichering. Daraus folgt meines Wissens nach die genau Messung der Zeitdilatation.
| TomS hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | Und mir war wichtig, – siehe letzter Beitrag im FAQ – dass der Wechsel zwischen Koordinatensystemen und der Wechsel zwischen Beobachtern sowohl physikalisch als auch mathematisch etwas völlig anderes ist.
Wenn das nicht klar wird, muss ich es nochmal herausstellen. |
Ja aber dazu muss man wissen was ko- bzw. kontravariant bedeutet. Diesen Unterschied gerne besser herausstellen. |
Du meinst die Rechenregel?
 = (t, x))
 = (x^0, -x^1) = (t, -x))
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
antaris
Anmeldungsdatum: 12.12.2022
Beiträge: 477
Wohnort: In einem chaotischen Universum
|
| antaris Verfasst am: 16. Feb 2024 18:45 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | antaris hat Folgendes geschrieben: | | Also geht es darum, dass Vektoren bei einer Koordinatentransformation die gleiche physikalische Bedeutung haben müssen? |
Ja.
| antaris hat Folgendes geschrieben: | | Die Koordinatentransformation entspricht einer Abbildung wie z.B. Translation, Rotation usw.? |
Ja. |
Und die Beobachtertransformation ist auch eine solche Abbildung, nur Lorentztransformiert?
| TomS hat Folgendes geschrieben: | | antaris hat Folgendes geschrieben: | | Dann besteht der Unterschied darin, dass der Beobachter ein Ereignis aus einem bestimmten Abstand beobachtet und bei Koordinatentrnsformation ein Ereignis von einer Raumzeit in eine andere hineintransformiert wird? |
Bei den meisten Berechnungen wird implizit vorausgesetzt, dass die Beobachtung lokal erfolgt, d.h. man berücksichtigt im Allgemeinen nicht, dass sich zunächst ein Lichtstrahl vom Ereignis zum Beobachter ausbreiten muss. Das ist ein weiterer Punkt, den ich oben ich ergänze. |
Ok klar. Es wird im allgemeinen immer gemessen was empfangen und nicht was gesendet wird.
| TomS hat Folgendes geschrieben: | | Nein, die Koordinatentransformation transformiert nicht zwischen zwei verschiedenen Raumzeiten, sondern zwischen zwei Koordinatensystemen für die selbe Raumzeit. Durch die Einführung verschiedener Weltkarten in Atlanten erzeugt du auch keine neuen Erden. |
Stimmt, das ist damit klar.
| TomS hat Folgendes geschrieben: | | antaris hat Folgendes geschrieben: | | Wenn ich also am Ereignis mehr oder weniger direkt vorbeifliege, dann messe ich die gleiche Länge, wie ein am Objekt ruhender Beobachter...weil sich das Ereignis und ich zu diesem Zeitpunkt annähernd in der "gleichen Raumzeit" befinden? |
Ich verstehe nicht genau, was du messen willst, aber ich fürchte, die Antwort lautet Nein. |
1. Wenn man einen Stab von Punkt P nach Punkt Q verschiebt, so ist dessen Länge bei beiden Punkten gleich?
2a. Wenn ein Beobachter danach von Punkt P nach Punkt Q reist, so unterliegt der Stab, aus Sicht des bewegten Beobachters, einer Längenkontraktion, die verschwindet, wenn der Beobachter an Punkt Q stoppt?
2b. Der Beobachter fliegt unbeschleunigt mit 0,5c an Punkt Q vorbei nach Punkt R. Die Längenkontraktion des Stabes ist während des unbeschleunigten Fluges an Q vorbei immer gleich?
Ein Ereignis in der Raumzeit zu verschieben, also seine Koordinaten zu transformieren, ist nicht das gleiche wie einen Beobachter real von P nach Q reisen zu lassen und somit eine Beobachtertransformation?
Was meinst du mit den Geraden, die sich auf der Ebene kreuzen?
|
|
|
antaris
Anmeldungsdatum: 12.12.2022
Beiträge: 477
Wohnort: In einem chaotischen Universum
|
| antaris Verfasst am: 16. Feb 2024 19:16 Titel: Re: Diskussion: FAQ - Zeitdilatation, Längenkontraktion, lin |
|
|
| TomS hat Folgendes geschrieben: | | antaris hat Folgendes geschrieben: | | Die Raumzeit im Abstand zweier Ereignisse mit einer Relativgeschwindigkeit zueinander, krümmt sich nicht Aufgrund der Zeitdilatation? |
Nee, da krümmt sich nichts. |
Super, ein Missverständnis weniger.
| TomS hat Folgendes geschrieben: | | antaris hat Folgendes geschrieben: | | Aber das ist doch genau das geometrische Bild, was man mit dem Minkowski-Diagramm so schön veranschaulichen kann. |
Schlimmstenfalls hast du sie falsch verstanden.
Sie veranschaulichen Koordinaten,achsen, Welt,linien von Beobachtern, Lichtstrahlen … Die quantitative Berechnung bzw. das Messen von Abständen ist jedoch nicht unmittelbar einsichtig. |
Ich war der Meinung, dass bei 1 setzen der Achsen die Zeitdilatation bzw. die Längenkontraktion prozentual abgelesen werden kann. Der Abstand muss aber über die Metrik berechnet werden?
| TomS hat Folgendes geschrieben: | | antaris hat Folgendes geschrieben: | | Ok, dann würde mir eine Übersetzung "kurzer Formalisums = langer Formalismus" helfen das besser zu verstehen. |
Können wir machen. |
Ich vermute da könnte allgemeines öffentliches Interesse bestehen.
| TomS hat Folgendes geschrieben: | | antaris hat Folgendes geschrieben: | | Ich weiß nicht. Beobachter bestehen aus Materie die Masse hat. |
Wie so oft verwendet man natürlich idealisierte Beobachter, die so klein und massearm sind, dass sie nie auf die Raumzeit wirken; sicher nicht in der SRT, denn da ist die Raumzeit starr, jedoch auch nicht in der ART. |
Umd noch eins weniger...
| TomS hat Folgendes geschrieben: | | antaris hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Insbs. versteht man nicht, dass die gemessenen Größen Lorentz-invariante Größen sind. |
Wenn wir das Myon auf der Erde Messen, dann doch nur aufgrund durch die Zeitdilatation der Koordinatenzeit t, bei der hoher Geschwindigkeit. Kann man die Eigenzeit eines solchen Myons direkt messen? |
Na, man müsste sozusagen neben her fliegen. |
Ok, das dachte ich mir auch.
| TomS hat Folgendes geschrieben: | | Was man an Beschleunigern tatsächlich messen kann, ist zum einen der Zerfall von im Speicherring kreisenden Elementarteilchen bzw. deren Zerfallsprodukte, zum anderen die Anzahl der Elementarteilchen im Speichering. Daraus folgt meines Wissens nach die genau Messung der Zeitdilatation. |
Die Frequenzen des Magnetfeldes werden mit der Zeitdilatation von z.B. einem Elektron im Speicherring synchronisiert, damit man höhere Geschwindigkeiten erreicht. Der Speicherring wird dann Synchrotron genannt. Ich war öfter im Bessy II in Berlin als auftragnehmender Dienstleister und konnte ein bischen was aufschnappen.
2022 wurde die Zeitdilatation zwischen 1 mm Radiusunterschied im Gravitationsfeld der Erde am genauesten vermessen.
https://www.scinexx.de/news/technik/einsteins-zeitdehnung-im-millimeter-massstab/
| TomS hat Folgendes geschrieben: |
Du meinst die Rechenregel?
|
Ja das sieht sehr zusammenfassend aus aber verstehe es nicht.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18081
|
| TomS Verfasst am: 16. Feb 2024 20:24 Titel: |
|
|
| Phoros hat Folgendes geschrieben: | | Kann man nicht an jeden Beobachter ein KS hängen? Das würde den Beobachter aber auch nicht "objektivieren", oder? |
Doch, das geht.
In der ART betrachtet man z.B. vereinzelt die Raumzeit vollständig und dicht ausfüllenden idealen = masselosen und in sich wechselwirkungsfreien Staub, der glatt (laminar) fließt. Dies führt bei einigen Problemen zu einer echt physikalischen Formulierung bzgl. des "Beobachtersystems Staub".
Der ADM-Formalismus kann ähnlich interpretiert werden.
| Phoros hat Folgendes geschrieben: | | In welchem Fallbeispiel wäre die identische Verwendung zweifelhaft? |
Technische immer dann, wenn die globale Extrapolation der lokalen Koordinaten scheitert oder unnötig kompliziert ist, z.B. der Rindler-Beobachter, oder in der ART der Schwarzschild-Beobachter.
Prinzipiell dann, wenn man den Unterschied nicht verstanden hat. Was zumeist nicht die eigene Schuld ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Phoros
Anmeldungsdatum: 08.02.2024
Beiträge: 13
|
| Phoros Verfasst am: 17. Feb 2024 09:46 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Prinzipiell dann, wenn man den Unterschied nicht verstanden hat. Was zumeist nicht die eigene Schuld ist. |
Dann will ich mal sehen, ob ich es verstanden habe: Zwillingsparadoxon.
Beide befinden sich in ihrem Inertialsystem, A im Ruhesystem (Erde), B im dazu mit konstanter Geschwindigkeit bewegten System. Bis hierher könnte man KS und Beobachter identifizieren, aber spätestens, wenn B seinen turn back macht, wechselt er vom Minkowski-KS ins beschleunigte Riemann-KS, obwohl die Beobachter die gleichen bleiben .... (Na, sicher bin ich mir nicht). Welche Rolle spielt die Eigenzeit von B hierbei?
(Ich bin mir auch nicht sicher, ob ich hier in den Thread so reinplatzen kann ... ist das ok?)
|
|
|
antaris
Anmeldungsdatum: 12.12.2022
Beiträge: 477
Wohnort: In einem chaotischen Universum
|
| antaris Verfasst am: 17. Feb 2024 10:12 Titel: |
|
|
| Phoros hat Folgendes geschrieben: |
(Ich bin mir auch nicht sicher, ob ich hier in den Thread so reinplatzen kann ... ist das ok?) |
Je mehr Köpfe sich beteiligen, umso mehr macht die Arbeit, die sich TomS macht, auch Sinn. Ich will an dieser Stelle auch noch betonen, dass ich das Angebot hochprofessionelles Wissen frei zu teilen, im allgemeinen sehr positiv empfinde und schätze. Ganz im Sinne der freiheitlichen Wissenschaften!
Jeder hat andere Interessensgebiete, Gedanken und Erfahrungen zu der Thematik. Warum sich nicht ebenso frei austauschen und den Mut aufbringen sich zu äußern und das alles zu bündeln.
Hier geht es m.E. einzig darum, etwas neues und im Detail exaktes zu lernen...das kann niemals schlecht oder gar störend sein.
|
|
|
Phoros
Anmeldungsdatum: 08.02.2024
Beiträge: 13
|
| Phoros Verfasst am: 17. Feb 2024 11:36 Titel: |
|
|
| antaris hat Folgendes geschrieben: | | Hier geht es m.E. einzig darum, etwas neues und im Detail exaktes zu lernen...das kann niemals schlecht oder gar störend sein. |
Thumbs up! Da gehe ich mit ...
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18081
|
| TomS Verfasst am: 18. Feb 2024 07:20 Titel: |
|
|
| Phoros hat Folgendes geschrieben: | Dann will ich mal sehen, ob ich es verstanden habe: Zwillingsparadoxon.
Beide befinden sich in ihrem Inertialsystem, A im Ruhesystem (Erde), B im dazu mit konstanter Geschwindigkeit bewegten System. Bis hierher könnte man KS und Beobachter identifizieren, aber spätestens, wenn B seinen turn back macht, wechselt er vom Minkowski-KS ins beschleunigte Riemann-KS, obwohl die Beobachter die gleichen bleiben … |
Ich würde für A bzw. B von Inertial- bzw. Nicht-Inertialsystem im Minkowski-Raum sprechen. Riemannsche Koordinaten klingen nach ART und gekrümmter Raumzeit; die liegt hier aber nicht vor. Die lokalen Koordinaten von B werden aufgrund der Beschleunigung nicht global gültig sein, möglicherweise verschwindet A hier zeitweise hinter einem Koordinaten-Horizont.
Der wesentliche Punkt ist, dass die Wahl der Koordinaten für die Berechnung invarianter Messgrößen nur insofern relevant ist, als dass die Berechnung möglichst einfach ist. Die resultierenden Werte sind unabhängig von der Wahl der Koordinaten, daher eben invariant.
| Phoros hat Folgendes geschrieben: | | Welche Rolle spielt die Eigenzeit von B hierbei? |
Sie ist zunächst eine derartige Messgröße. Ich zeige gleich noch eine andere Berechnung.
Verwendet man sie als Koordinatenzeit, so werden die Koordinaten während der Beschleunigung ekelhaft kompliziert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18081
|
| TomS Verfasst am: 18. Feb 2024 07:35 Titel: |
|
|
Hier die Koordinaten eines Beobachters, der zeitweise eine Kreisbahn beschreibt:
https://en.m.wikipedia.org/wiki/Born_coordinates
Das ist ziemlich kompliziert, also werden wir diese Koordinaten möglichst vermeiden.
Wir betrachten zwei Beobachter a=1,2, die an einem Raumzeitpunkt P gemeinsam zu einer Reise starten, und wiederum gemeinsam bei Q diese Reise beenden. Dazwischen bewegen sie sich mit jeweils konstanter Bahngeschwindigkeit v_a auf einer Kreisbahn mit Radius R_a.
Wir betrachten dies aus Sicht eines Intertialsystems. Die Koordination von P und Q lauten
_P = (0, 0, 0))
_Q = (T, 0, 0))
x,y sind kartesische Koordinaten in der Ebene; die dritte Raumdimension z benötigen wir nicht.
In einer 2+1 dim. Raumzeit mit t als dritter Dimension entspricht eine Reise einer Schraubenlinie, die am Ursprung startet und nach einer Zeit T wieder zu x=y=0 zurückkehrt.
Auf der Uhr eines bei x=y=0 ruhenden Beobachters vergeht die Zeit T, d.h. die Koordinatenzeit T entspricht der Eigenzeit dieses Beobachters. Wir können diesen Beobachter einführen, müssen dies aber nicht; die Koordinaten sind reine Rechengrößen.
Damit A und B ihre Reise gemeinsam beginnen und beenden können, muss für ihre Geschwindigkeiten in den o.g. Koordinaten entlang der Kreisbahnen gelten
Wir gehen aus von der Formel für die Zeitdilatation der Eigenzeit tau eines mit konstanter, linearer Geschwindigkeit v bewegten Beobachters, bzgl. des o.g. Koordinatensystems. D.h.
Die x- und y-Komponenten der Geschwindigkeit ändern sich entlang der Kreisbahn, der Betrag v jedoch nicht. Die Kreisbahn sei sozusagen zusammengesetzt aus unendlich vielen infinitesimal kleinen Abschnitten.
Integration liefert
Links steht die für den Reisenden vergangene Eigenzeit. Da v konstant ist *) folgt
Angewandt auf unsere beiden Reisenden a=1,2 gilt
Je größer der Kreis, desto größer die Geschwindigkeit, bei fester und für beide identische Zeit T.
Wir können nun drei Eigenzeiten also Messgrößen vergleichen.
Verzichten wir jedoch auf die Betrachtung des dritten Beobachters, eliminieren wir also T mittels Division, so folgt
Die Eigenzeiten sind Messgrößen auf den mitgeführten Uhren, die Geschwindigkeiten können ebenfalls gemessen werden, z.B. mittels Zentrifugalbeschleunigung oder Rotverschiebung von Lichtsignalen bekannter Frequenz.
Oder, wenn wir T mittels des zuvor vermessenen Kreisradius (einer Art invarianten Ruhelänge) ausdrücken:
 )
In allen Fällen verschwinden die Koordinaten aus dem Endergebnis, es bleiben ausschließlich invariante Größen zurück – wobei man im Einzelfall aus der Rechnung ablesen oder anderweitig beweisen muss, dass invariante Größen vorliegen.
Die Beobachter a=1,2 haben wir dabei nie mit irgendwelchen Koordinatensystemen assoziieren müssen; wer das tun möchte, darf gerne die Mathematik im o.g. Link durcharbeiten.
Das ist eigentlich die zentrale Botschaft: die Relativitätstheorie geht aus von der Invarianz der Lichtgeschwindigkeit, nimmt einen kurzen Umweg über die Relativität der Gleichzeitigkeit, und betrachtet dann zumeist wieder invariante Messgrößen, die unabhängig von Koordinatensystem sind – daher invariant – jedoch beobachter-spezifisch.
*) die Formel mit Integration würde sofort auch für zeitabhängiges v(t) gelten, mit einer geeigneten auch für die ART
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
MBastieK
Anmeldungsdatum: 06.10.2012
Beiträge: 951
Wohnort: Berlin-Wedding
|
| MBastieK Verfasst am: 18. Feb 2024 13:22 Titel: |
|
|
| TomS hat Folgendes geschrieben: |
Die x- und y-Komponenten der Geschwindigkeit ändern sich entlang der Kreisbahn, der Betrag v jedoch nicht. Die Kreisbahn sei sozusagen zusammengesetzt aus unendlich vielen infinitesimal kleinen Abschnitten.
Integration liefert
|
Stimmt hier was mit den Einheiten nicht?
Damit
funktioniert, muss v² einheitenlos sein, aber das ist es durch
aber nicht, da dx/dt die Geschwindigkeits-Einheit hat.
Ich kenne
als
mit ß = v/c, was es einheitenlos macht.
Nette Grüsse
_________________
Intelligenz ist die Fähigkeit der (temporären) Anpassung. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18081
|
| TomS Verfasst am: 18. Feb 2024 15:33 Titel: |
|
|
Genauso ist das. Theoretische Physiker setzten meist
d.h. v wird in Bruchteilen von c gemessen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
MBastieK
Anmeldungsdatum: 06.10.2012
Beiträge: 951
Wohnort: Berlin-Wedding
|
| MBastieK Verfasst am: 18. Feb 2024 16:14 Titel: |
|
|
| TomS hat Folgendes geschrieben: | Genauso ist das. Theoretische Physiker setzten meist
d.h. v wird in Bruchteilen von c gemessen. |
Dann ist v quasi die Verhältnismäßigkeit, die man sonst durch ß ausdrückt!?!
Nette Grüsse
_________________
Intelligenz ist die Fähigkeit der (temporären) Anpassung. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18081
|
| TomS Verfasst am: 18. Feb 2024 16:22 Titel: |
|
|
Ja.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Phoros
Anmeldungsdatum: 08.02.2024
Beiträge: 13
|
| Phoros Verfasst am: 18. Feb 2024 18:36 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | Riemannsche Koordinaten klingen nach ART und gekrümmter Raumzeit; die liegt hier aber nicht vor. Die lokalen Koordinaten von B werden aufgrund der Beschleunigung nicht global gültig sein. |
Jep, got it! Wir bewegen uns ja nicht im Grav.-feld.
| TomS hat Folgendes geschrieben: | | Verwendet man sie (die Eigenzeit, Ph.) als Koordinatenzeit, so werden die Koordinaten während der Beschleunigung ekelhaft kompliziert. |
Würde das die Identifikation von KS und Beobachter bedeuten?
| TomS hat Folgendes geschrieben: | | Der wesentliche Punkt ist, dass die Wahl der Koordinaten für die Berechnung invarianter Messgrößen nur insofern relevant ist, als dass die Berechnung möglichst einfach ist. Die resultierenden Werte sind unabhängig von der Wahl der Koordinaten, daher eben invariant. |
D.h. „die Priorität, der Akzent, …“ liegt bei den Beobachtern, während die KS lediglich mathematische Hilfsmittel zur Ermittlung der Bewegungszustände der Beteiligten sind?
| TomS hat Folgendes geschrieben: | | Das ist eigentlich die zentrale Botschaft: die Relativitätstheorie geht aus von der Invarianz der Lichtgeschwindigkeit, nimmt einen kurzen Umweg über die Relativität der Gleichzeitigkeit, und betrachtet dann zumeist wieder invariante Messgrößen, die unabhängig von Koordinatensystem sind – daher invariant – jedoch beobachter-spezifisch. |
Invarianz (c) ist die Voraussetzung der Speziellen Relativitätstheorie, Relativität d. Gleichzeitkt. ihre Folge … dann wird mit invarianten Messgrößen und geeigneten Koordinaten/Lorentz-Formalismen das Szenario berechnet?
Jetzt habe ich aber vom Zwillingsparadoxon (mit  und  gesprochen, bei dir reisen sie zusammen. Das ist wohl dann der allgemeine Fall mit v_relativ ungleich Null.
Fazit: Es wird eine bestimmte vorgegebene Beobachter-Konstellation angenommen (Priorität) und diese dann durch die Wahl geeigneter (= möglichst einfacher) Koordinaten berechnet. In diesem Sinne ist es so, dass KS nicht unbedingt Beobachter repräsentieren wie ein Tensor eine Größe, sondern dass dessen geeignet gewählte Koordinaten für die Berechnung verwendet werden.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18081
|
| TomS Verfasst am: 18. Feb 2024 22:13 Titel: |
|
|
| Phoros hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Verwendet man sie (die Eigenzeit, Ph.) als Koordinatenzeit, so werden die Koordinaten während der Beschleunigung ekelhaft kompliziert. |
Würde das die Identifikation von KS und Beobachter bedeuten? |
Ja, in diesem Falle entspräche das einem (vorübergehend) mitrotierenden Beobachter.
| Phoros hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | | Der wesentliche Punkt ist, dass die Wahl der Koordinaten für die Berechnung invarianter Messgrößen nur insofern relevant ist, als dass die Berechnung möglichst einfach ist. Die resultierenden Werte sind unabhängig von der Wahl der Koordinaten, daher eben invariant. |
D.h. „die Priorität, der Akzent, …“ liegt bei den Beobachtern … |
Letztlich bei den beobachtbaren bzw. messbaren Größen.
| TomS hat Folgendes geschrieben: | | Das ist eigentlich die zentrale Botschaft: die Relativitätstheorie geht aus von der Invarianz der Lichtgeschwindigkeit, nimmt einen kurzen Umweg über die Relativität der Gleichzeitigkeit, und betrachtet dann zumeist wieder invariante Messgrößen, die unabhängig von Koordinatensystem sind – daher invariant – jedoch beobachter-spezifisch. |
Invarianz (c) ist die Voraussetzung der Speziellen Relativitätstheorie, Relativität d. Gleichzeitkt. ihre Folge … dann wird mit invarianten Messgrößen und geeigneten Koordinaten/Lorentz-Formalismen das Szenario berechnet?
Jetzt habe ich aber vom Zwillingsparadoxon (mit und gesprochen, bei dir reisen sie zusammen. Das ist wohl dann der allgemeine Fall mit v_relativ ungleich Null.
Fazit: Es wird eine bestimmte vorgegebene Beobachter-Konstellation angenommen (Priorität) und diese dann durch die Wahl geeigneter (= möglichst einfacher) Koordinaten berechnet. In diesem Sinne ist es so, dass KS nicht unbedingt Beobachter repräsentieren wie ein Tensor eine Größe, sondern dass dessen geeignet gewählte Koordinaten für die Berechnung verwendet werden.[/quote] :lolhammer:
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5873
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
