| Autor |
Nachricht |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 17245
|
 TomS Verfasst am: 23. Mai 2015 09:45 Titel: FAQ - kosmologische Expansion - Ameise auf einem Gummiband |
 |
|
Man stelle sich ein ideales Gummiband vor, das sich gleichmäßig unendlich lang ausdehnen kann. Man stelle sich weiterhin eine ideale, punktförmige Ameise vor.
Wenn das Gummiband zum Zeitpunkt 0 einen Kilometer Länge misst und zu diesem Zeitpunkt die Ameise sich an einem Ende des Gummibandes befindet, und wenn sich das Gummiband um einen Kilometer pro Sekunde ausdehnt, während die Ameise sich mit einem Zentimeter pro Sekunde fortbewegt, dann stellt sich die Frage: Erreicht die Ameise das andere Ende des Gummibandes, und wenn ja wie lange braucht sie?
Wie lautet die allgemeine Lösung, wenn das Gummiband zu Beginn die Länge L_0 hat, sich zu jedem Zeitpunkt t um einen beliebigen Faktor a(t) ausdehnt, also
 = L_0 \, a(t))
und wenn die Ameise die konstante Geschwindigkeit v=c hat?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 17245
|
| TomS Verfasst am: 25. Mai 2015 11:32 Titel: |
|
|
Man analysiert den allgemeinen Fall
 = L_0\,a(t))
Zur Aufstellung der DGL betrachten wir die infinitesimale Expansion des gesamten Bandes
}{L(t)} = \frac{L(t)+\dot{L}(t)\,dt}{L(t)} = 1+\frac{\dot{a}}{a}\,dt)
Um diesen Faktor werden alle Längen zu jedem Zeitpunkt t in einen infinitesimalen Zeitintervall dt gedehnt.
Nun betrachten wir die Wanderung der Ameise
 = x(t) + \dot{x}(t)\,dt \stackrel{!}{=} \left[x+c\,dt\right]\,\left[1+\frac{\dot{a}}{a}\,dt\right])
Die beiden Klammern nach dem zweiten = bedeuten, dass die Ameise zum Einen eine infinitesmale Strecke c dt zurücklegt, und diese zum Anderen zugleich um den oben berechneten Faktor gedehnt wird. Ausmultiplizieren, Vernachlässigen infinitesimaler Größen dt² zweiter Ordnung sowie Zusammenfassen liefert die DGL
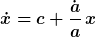
Diese kann man direkt zu lösen versuchen. Einfacher wird es jedoch, wenn man statt x eine mit L reskalierte Größe xi betrachtet, so dass der Gesamtlänge L zu jedem Zeitpunkt Eins und dem Weg der Ameise ein gewisser Bruchteil davon entspricht.
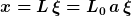
Einsetzen in die DGL liefert auf der linken Seite
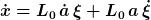
sowie auf der rechten Seite
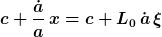
Anstelle der Zeitabhängigkeit von x betrachten wir also die Zeitabhängigkeit von xi; dabei fällt die triviale Zeitabhängigkeit von L bzw. a teilweise heraus, d.h. die neue DGL in xi ist einfacher als die in x:
Daraus folgt durch Trennung der Variablen
 = \frac{c}{L_0}\int_0^t \frac{ds}{a(s)})
 = c\,a(t)\int_0^t \frac{ds}{a(s)})
Und damit ist auch klar, wie man berechnet, ob die Ameise bei x(t) das Ende des Bandes bei L(t) erreicht: in der reskalierten Gleichung für xi gilt dies genau dann, wenn es ein t=T gibt, für das xi gleich eins wird, also wenn
 \stackrel{!}{=} 1)
In Abhängigkeit der genauen Form von a(t) kann die Ameise den ursprünglich mit L_0 markierten Punkt erreichen oder auch nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 10. Jan 2016 23:26, insgesamt einmal bearbeitet |
|
|
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 906
Wohnort: Mintraching
|
| Ich Verfasst am: 25. Mai 2015 22:13 Titel: |
|
|
| TomS hat Folgendes geschrieben: | | In Abhängigkeit der genauen Form von a(t) kann die Ameise den ursprünglich mit L_0 markierten Punkt erreichen oder auch nicht. |
...und jetzt wär's interessant, zu dieser genauen Form etwas zu sagen. Nämlich, ob ein Lichtsignal unendlich weit kommt oder eben nicht.
t soll jetzt die Zeit seit dem Urknall sein, das Lichtsignal werde zum Zeitpunkt t0 losgeschickt, wo a(t0) einen von Null verschiedenen Wert hat.
Setzen wir als Zeitverlauf für die Expansion des Universums einfach mal an
 \propto t^n) , so dass die Expansion für n<1 gebremst ist und für n>1 beschleunigt.
Dann ist
 \propto \int_{t0}^t \frac{ds}{a(s)}=\int_{t0}^t t^{-n}{ds} \propto t^{1-n}-\textbf{irgendwas})
genau dann finit, wenn n>1 ist. Sprich: wenn die Expansion beschleunigt ist.
Das heißt, dass bei unbeschleunigter (oder gebremster) Expansion sich kein Horizont ausbildet und ein Lichtsgnal immer unendlich weit kommt, wenn man lange genug wartet.
Der Ansatz ist natürlich nicht allgemeingültig, unser Universum z.B. folgt einer anderen Formel. Er ist aber nicht schlecht, weil er einige wichtige Spezialfälle abdeckt:
n=1/2: strahlungsdominiertes Universum (ungefähr die ersten 200000 Jahre unseres Universums)
n=2/3: flaches, materiedominiertes Universum (ungefähr die nächste Milliarde Jahre unseres Universums)
n=1: "free floating", unbeschleunigtes Universum. In Wirklichkeit nur in der Zeit vor ~7 Mrd Jahren realisiert, aber ungemein wichtig als das Spielzeugmodell eines leeren Universums - bzw. eines Universums unter Vernachlässigung von Gravitation, das also auch ohne ART berechenbar ist.
Die grundsätzliche Erkenntnis bleibt aber (ohne Beweis): Horizont nur bei Beschleunigung der Expansion, und auch dann nur, wenn die Beschleunigung unendlich lange währt. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 17245
|
| TomS Verfasst am: 02. Jun 2015 21:52 Titel: |
|
|
Ich würde gerne zunächst zeigen, dass die Gleichungen für lichtartige Geodäten sowie für die oben betrachtete Ameise tatsächlich strukturell auf die selbe Gleichung führen.
Man betrachtet das Linienelement = die Eigenzeit für ein FRW-Universum
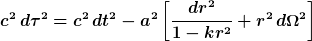
r,t bezeichnen Koordinaten, tau die Eigenzeit, a(t) den Skalenfaktor, der die Expansion des Universums beschreibt. Wir betrachten eine sich radial bewegendes Photon, d.h. die in Omega zusammengefassten Winkel sind konstant. Zudem liegt für ein Photon eine Null-Geodäte vor, d.h. tau ist Null.
Im folgenden betrachte ich außerdem der Einfachheit halber ein flaches Universum mit k = 0.
Damit folgt für das Linienelement, für die Bewegungsgleichung sowie für deren Lösung mittels Integration
})
 - r_0 = \pm c \int_{t_0}^t \frac{ds}{a(s)})
Wir betrachten nun aus Sicht eines Beobachters bei r = 0 ein - von einem bei (t_0, r_0) lokalisierten Lichtblitz - einlaufendes Photonen und berechnen, zu welchem Zeitpunkt t dieses bei r = 0 eintrifft. Die zu lösende Gleichung lautet:
})
Die Lösungen dieser Gleichungen hängen vom selben Integral ab wie im o.g. Beispiel.
Im Folgenden möchte ich für spezielle Formen des Skalenfaktors a(t) diskutieren, unter welchen Bedingungen diese Gleichung lösbar ist. Zunächst ist offensichtlich klar, dass wenn das Integral für beliebige Zeiten t beschränkt bleibt, immer eine Koordinate r_0 gefunden werden kann, die größer ist als der Wert des Integrals. D.h. wenn
} < \infty)
dann existieren
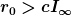
für die die Gleichung keine Lösung
hat! Dies entspricht der Existenz eines Sichtbarkeitshorizontes. Umgekehrt ist klar, dass wenn das Integral unbeschränkt ist, zu jedem r_0 ein geeignetes t gefunden werden kann, so dass die Gleichung immer lösbar ist.
Ich setze dabei
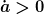
voraus, was für die im Folgenden zu diskutierenden Universen immer zutrifft.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 17245
|
| TomS Verfasst am: 02. Jun 2015 23:16 Titel: |
|
|
Einige wesentlichen Betrachtungen hat Ich schon angestellt. Daher hier zunächst nur eine kurze Zusammenfassung: wir betrachten
 = (\kappa t)^\mu)
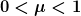
Für das materie- bzw. strahlungs-dominierte Universum mit mu = 2/3 bzw. mu = 1/2 folgt
} = \int_{\kappa t_0}^{\kappa t} \frac{dz}{\kappa z^\kappa} = \frac{(\kappa t_0)^\nu}{\nu\kappa}\,\left[\left(\frac{t}{t_0}\right)^\nu - 1\right])
mit
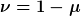
Offensichtlich fallen diese Skalenfaktoren in die Klasse der Universen ohne Horizont; die o.g. Gleichungen sind immer lösbar.
Anders sieht es für den Skalenfaktor
 = a_0\,e^{\kappa t})
d.h. das vakuum-dominierte deSitter-Universum mit kosmologischer Konstante aus:
} = a_0 \int_{\kappa t_0}^{\kappa t} \frac{dz}{\kappa e^z} = \frac{a_0}{\kappa}e^{-\kappa t_0} \left[1-e^{-\kappa (t - t_0)}\right])
Insbs. gilt
} = \frac{a_0}{\kappa}e^{-\kappa t_0} < \infty)
Lösung der Gleichung für vorgegebenes (t_0, r_0) führt auf
} = 1 - \frac{\kappa r_0}{c a_0} e^{\kappa t_0})
Die linke Seite ist strikt positiv, die rechte Seite kann jedoch für
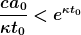
auch negativ werden. D.h. dass bei vorgegebener Zeit t_0 immer ein (genügend großes) r_0 gefunden werden kann, so dass die Gleichung keine Lösung hat. In diesem Fall liegt ein Sichtbarkeitshorizont vor.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 17245
|
| TomS Verfasst am: 26. Jan 2022 09:56 Titel: |
|
|
Noch eine Anmerkung zur Nichterhaltung der Energie.
Man betrachtet die Expansion einer gegebenen Länge
mit der infinitesimale Expansion
sowie die Bewegung der Ameise oder eines anderen Tieres; die Geschwindigkeit u sei je Tierart fest und konstant, kann jedoch zwischen den Tierarten variieren.
 = x(t) + \dot{x}(t)\,dt \stackrel{!}{=} \left[x+u\,dt\right]\,\left[1+\frac{\dot{a}}{a}\,dt\right])
Ausmultiplizieren, Vernachlässigen infinitesimaler Größen dt² zweiter Ordnung sowie Zusammenfassen liefert die DGL
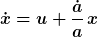
Diese vereinfacht sich mittels Reskalieren
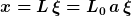
zu
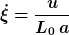
bzw.
Für die Definition der Energie betrachten wir die Lagrangefunktion
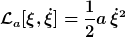
Daraus folgt mittels der Euler-Lagrange-Gleichung der erhaltene konjugierte Impuls
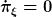
Die oben eingeführte Geschwindigkeit u folgt hier als Integrationskonstante im Zuge der Lösung der Bewegungsgleichung.
Die Impulserhaltung folgt letztlich mittels Noether-Theorem aus der Invarianz unter Orts-Translationen; der Ort xi ist eine zyklische Variable.
Analog findet man nun die Energie
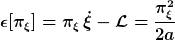
mittels Noether-Theorem und Zeit-Translationen. Diese ist jedoch nicht erhalten, da für eine Lösung der Bewegungsgleichung und mittels Impulserhaltung folgt
_________________
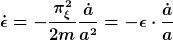
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
