| Autor |
Nachricht |
Brillant

Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
 Brillant Verfasst am: 24. Jul 2016 12:24 Titel: Expansion des Universums Brillant Verfasst am: 24. Jul 2016 12:24 Titel: Expansion des Universums |
 |
|
Warum wird eigentlich angenommen, es müsste im Universum eine Kraft (negative Gravitation) herrschen, die das All auseinander treibt?
Wenn ich Vakuum räumlich vergrößere, brauche ich überhaupt keine Kraft.
Ich stelle mir folgende Versuchsanordnung vor:
In einen sekrecht stehenden, unten geschlossenen Zylinder taucht ein gegen die Zylinderwand gasdicht schließender Kolben ein. Der Kolben wird an einem Seil nach oben gezogen, das Seil läuft um eine Rolle und wird am anderen Ende mit einem Gewicht belastet, das genau den Luftdruck ausgleicht, der auf den Kolben drückt.
Nun kann ich vollkommen ohne Kraft (okay, die Reibung der Dichtung muss durch ein Zusatzgewicht überwunden werden) das Vakuum im Kolben beliebig vergrößern, indem ich dem Gewicht einen minimalen Impuls nach unten gebe.Dafür brauche ich innen gar keinen Urknall oder Ähnliches.
Ist die Behauptung richtig oder falsch?
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 24. Jul 2016 22:47 Titel: Re: Expansion des Universums TomS Verfasst am: 24. Jul 2016 22:47 Titel: Re: Expansion des Universums |
 |
|
| Brillant hat Folgendes geschrieben: | | Warum wird eigentlich angenommen, es müsste im Universum eine Kraft herrschen, die das All auseinander treibt? |
Es wird keine Kraft angenommen.
Man formuliert im Rahmen der ART ein Modell.
Dabei war es nicht das Ziel, diese Expansion zu beschreiben, denn die war damals noch gar nicht bekannt. Ziel war es, die Gravitation im lokalen Maßstab plus die Dynamik des Universums im globalen Maßstab zu beschreiben. Dabei folgt die Expansion automatisch und ohne Zusatzannahmen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 25. Jul 2016 18:42 Titel: DrStupid Verfasst am: 25. Jul 2016 18:42 Titel: |
 |
|
|
Ich glaube er meint die beschleunigte Expansion.
|
|
 |
yukterez

Anmeldungsdatum: 20.09.2014
Beiträge: 96
|
 yukterez Verfasst am: 25. Jul 2016 19:30 Titel: yukterez Verfasst am: 25. Jul 2016 19:30 Titel: |
 |
|
| Zitat: | | Warum wird eigentlich angenommen, es müsste im Universum eine Kraft (negative Gravitation) herrschen, die das All auseinander treibt? |
Weil der Hubbleparameter ohne kosmologische Konstante viel schneller durch normale Gravitation abgebremst werden würde. Als Analogie kannst du dir einen Stein vorstellen der obwohl du ihn mit weniger als seiner Fluchtgeschwindigkeit wirfst trotzdem in die Unendlichkeit entkommt. Das geht natürlich nur wenn der Stein eine eigene Energiequelle, z.B. einen Raketenantrieb der ihn beschleunigt, hat.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Jul 2016 19:53 Titel: TomS Verfasst am: 25. Jul 2016 19:53 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | Ich glaube er meint die beschleunigte Expansion. |
Auch da wird keine Kraft angenommen.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Jul 2016 19:55 Titel: TomS Verfasst am: 25. Jul 2016 19:55 Titel: |
 |
|
| yukterez hat Folgendes geschrieben: | | Zitat: | | Warum wird eigentlich angenommen, es müsste im Universum eine Kraft (negative Gravitation) herrschen, die das All auseinander treibt? |
Weil der Hubbleparameter ohne kosmologische Konstante viel schneller durch normale Gravitation abgebremst werden würde. Als Analogie kannst du dir einen Stein vorstellen der obwohl du ihn mit weniger als seiner Fluchtgeschwindigkeit wirfst trotzdem in die Unendlichkeit entkommt. Das geht natürlich nur wenn der Stein eine eigene Energiequelle, z.B. einen Raketenantrieb der ihn beschleunigt, hat. |
Auch im Falle der (beschleunigten) Expansion existiert keine Kraft, keine eigene Energiequelle und kein eigener Antrieb.
Alle Objekte bewegen sich kräftefrei mit dem (beschleunigt) expandierenden Universumm mit.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 25. Jul 2016 23:12 Titel: DrStupid Verfasst am: 25. Jul 2016 23:12 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Auch da wird keine Kraft angenommen. |
Aber etwas, was man als "negative Gravitation" umschreiben kann. Wenn Du nicht bemerkt hast, dass Brillant den Begriff "Kraft" an dieser Stelle nur in Unkenntnis korrekter Formulierungen verwendet hat, dann dürfte bereits Dein erster Beitrag am Ziel vorbei gegangen sein.
|
|
 |
Günther
Anmeldungsdatum: 23.11.2010
Beiträge: 330
|
 Günther Verfasst am: 26. Jul 2016 11:18 Titel: Günther Verfasst am: 26. Jul 2016 11:18 Titel: |
 |
|
|
"was das All auseinander treibt" ist nun mal keine Kraft, gleichgültig ob das Universum gebremst oder beschleunigt expandiert. Tom ist auf dieses Verständnisproblem eingegangen. Da gibt's doch nichts zu bekritteln.
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 26. Jul 2016 18:13 Titel: DrStupid Verfasst am: 26. Jul 2016 18:13 Titel: |
 |
|
| Günther hat Folgendes geschrieben: | | "was das All auseinander treibt" ist nun mal keine Kraft, gleichgültig ob das Universum gebremst oder beschleunigt expandiert. Tom ist auf dieses Verständnisproblem eingegangen. Da gibt's doch nichts zu bekritteln. |
Sicher? Für mich sieht es so aus, als ob Brillant das, "was das All auseinander treibt" für eine Kraft hält und außerdem die Expansion des Universums mit der Beschleunigung derselben verwechselt. Wenn man unter diesen Bedingungen auf seine Frage, warum eine Kraft als Ursache der Expansion angenommen wird, antwortet, dass keine Kraft angenommen wird und die Expansion bereits vor ihrer Entdeckung aus den kosmologischen Modellen folgte (was korrekt ist), dann wird bei ihm ankommen, dass man nichts annimmt, "was das All auseinander treibt" und dass die beschleunigte Expansion schon Teil der ersten kosmologischen Modelle war (was nicht korrekt ist). Das wird seine Verwirrung nur noch vergrößern. Jemand wie er, der die Ursache für derartige Unstimmigkeiten eher selten bei sich selbst sucht, wird sich dadurch in seinem Glauben bestätigt fühlen, dass mit den kosmologischen Modellen etwas faul sein muss. Hälst Du das für wünschenswert?
|
|
 |
borromeus
Anmeldungsdatum: 29.12.2014
Beiträge: 509
|
 borromeus Verfasst am: 26. Jul 2016 19:57 Titel: borromeus Verfasst am: 26. Jul 2016 19:57 Titel: |
 |
|

|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 26. Jul 2016 22:09 Titel: TomS Verfasst am: 26. Jul 2016 22:09 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | Jemand wie er, der die Ursache für derartige Unstimmigkeiten eher selten bei sich selbst sucht, wird sich dadurch in seinem Glauben bestätigt fühlen, dass mit den kosmologischen Modellen etwas faul sein muss. |
Ich schlage vor, du löst das Problem dadurch, dass du eine physikalisch korrekte und zugleich Brillant zufriedenstellende Erklärung lieferst.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Brillant

Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
 Brillant Verfasst am: 26. Jul 2016 22:10 Titel: Brillant Verfasst am: 26. Jul 2016 22:10 Titel: |
 |
|
Es mag ja sein, dass die Physiker an ihrem Stammtisch einiges wissen, was aber keinesfalls an die Öffentlichkeit kommen darf.
Da ich nicht zu den Stammtisch-Teilnehmern gehöre, habe ich das Gerücht über dunkle Energie, die das All auseinander treibt, wohl wieder falsch verstanden.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 26. Jul 2016 22:21 Titel: TomS Verfasst am: 26. Jul 2016 22:21 Titel: |
 |
|
Wir haben etwas gegen den Begriff "Kraft", denn mit dem assoziiert man eine messbare Kraft. Und wir haben etwas dagegen, nur der kosmologischen Konstante einen solchen Effekt zuzuschreiben; das kann die ART ohne kosmologischen Konstante ganz alleine.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 26. Jul 2016 22:28 Titel: DrStupid Verfasst am: 26. Jul 2016 22:28 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Ich schlage vor, du löst das Problem dadurch, dass du eine physikalisch korrekte und zugleich Brillant zufriedenstellende Erklärung lieferst. |
So eine Erklärung gibt es nicht. Ich löse das Problem dadurch, dass ich ihm gar nicht antworte.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 26. Jul 2016 22:29 Titel: TomS Verfasst am: 26. Jul 2016 22:29 Titel: |
 |
|
Das ist natürlich auch OK
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 26. Jul 2016 23:39 Titel: Ich Verfasst am: 26. Jul 2016 23:39 Titel: |
 |
|
Typen wie Brillant zufriedestellen zu wollen ist nun wirklich albern.
Gravitation ist eine Scheinkraft. Die Kraft, die den Apfel auf Newtons Kopf zog, existiert nicht wirklich. Das hat sich allerdings nicht bis in die Schulphysik rumgesprochen, und auch die "breite Öffentlichkeit" kennt Gravitation als Kraft. Insbesondere die interessierte, dann zugegebenermaßen wesentlich schmalere, Öffentlichkeit ist mit dem Konzept der Gravitationskraft wohlvertraut und kann damit gut und intuitiv umgehen.
Da die Beschleunigung der Expansion nun auf abstoßende Gravitation zurückzuführen ist, halte ich es auch nicht für verkehrt, als ursächliche Kraft eben eine solche zu nennen, wenn den schon nach "Kraft" gefragt ist. Da macht man nichts falsch.
|
|
 |
yukterez

Anmeldungsdatum: 20.09.2014
Beiträge: 96
|
 yukterez Verfasst am: 27. Jul 2016 00:14 Titel: yukterez Verfasst am: 27. Jul 2016 00:14 Titel: |
 |
|
|
Als was auch immer man die Gravitation bezeichnet, eines ist auf jeden Fall klar: durch ihre Gezeitenkräfte kann man nicht nur spaghettifiziert sondern regelrecht zerrissen werden.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 27. Jul 2016 09:03 Titel: TomS Verfasst am: 27. Jul 2016 09:03 Titel: |
 |
|
|
Gezeitenkräfte sind nicht-lokale Effekte und letztlich keine eigenständigen Kräfte.
|
|
 |
Günther
Anmeldungsdatum: 23.11.2010
Beiträge: 330
|
 Günther Verfasst am: 27. Jul 2016 16:03 Titel: Günther Verfasst am: 27. Jul 2016 16:03 Titel: |
 |
|
Mitbewegte Objekte beschreiben Geodäten, sind also kräftefrei. Verbindet man zwei mitbewegte Objekte mechanisch, sind sie nicht mehr kräftefrei. Von Ersterem handelt die ART.
Natürlich ist die Frage, was das All auseinander treibt, berechtigt. Vielleicht kann man es salopp den "Urschwung" nennen, der ihm bei seiner Entstehung als abstoßend wirkende Gravitation aufgeprägt war. Jedenfalls waren bereits zu diesem Zeitpunkt t = 0 fiktive Testpartikel kräftefrei.
Die dunkle Energie wird - nicht nur hier - immer wieder mit einer Kraft in Verbindung gebracht und ebenso oft wird das richtig gestellt. Man kann schon auf den nächsten warten, der es nicht mitgekriegt hat.
|
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 27. Jul 2016 16:53 Titel: Ich Verfasst am: 27. Jul 2016 16:53 Titel: |
 |
|
Nochmal: Wenn man Gravitation als Kraft bezeichnet, wie es die Schulphysik, die Ingenieurswissenschaften, die Populärwissenschaft und eigentlich alle Leute ohne ausdrücklichem Hang zur ART tun, dann sind Testpartikel nicht kräftefrei. Und dann gibt es auch Gezeitenkräfte.
Es hat m.E. überhaupt keinen Wert, dann ohne weitere Erläuterungen darauf zu bestehen, dass keine Kräfte die Expansion beeinflussten.
Ich wiederhole nochmal: der Ablauf der Expansion wird durch die Gravitation beeinflusst. Ob man dazu Gravitationskraft sagt oder nicht ist überhaupt nicht Gegenstand der Fragen.
Eine hilfreiche Antwort wäre z.B. dass die Expansion von abstoßender Gravitation beschleunigt wird (Verursacher: DE). Wenn man will, kann man noch dazusagen, dass die Gravitationskraft in der ART als Scheinkraft identifiziert wird und man daher im strengen Sinne nicht von Gravitation als "Kraft" reden sollte.
Stattdessen nur zu sagen, dass auf die Expansion keine Kräfte wirken ist unhilfreich bis hin zu irreführend. Eine Themaverfehlung, darum geht es in den Fragen nämlich gar nicht.
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 27. Jul 2016 17:57 Titel: DrStupid Verfasst am: 27. Jul 2016 17:57 Titel: |
 |
|
| Ich hat Folgendes geschrieben: | | Nochmal: Wenn man Gravitation als Kraft bezeichnet, wie es die Schulphysik, die Ingenieurswissenschaften, die Populärwissenschaft und eigentlich alle Leute ohne ausdrücklichem Hang zur ART tun, dann sind Testpartikel nicht kräftefrei. Und dann gibt es auch Gezeitenkräfte. |
Zwischen Testpartikeln in einem unendlichen Newtonschen Universum gibt es zwar klar definierte Gezeitenkräfte, aber die Gravitationskräfte selbst sind unbestimmt. In Abhängigkeit von der Wahl des Bezugssystems können sie jeden beliebigen Wert annehmen. Damit sind Gravitationskräfte in der Kosmologie selbst im klassischen Fall ein ziemlich grenzwertiges Konzept.
| Ich hat Folgendes geschrieben: | | Es hat m.E. überhaupt keinen Wert, dann ohne weitere Erläuterungen darauf zu bestehen, dass keine Kräfte die Expansion beeinflussten. |
Da gebe ich Dir allerdings Recht. Es muss zumindest darauf hingewiesen werden, dass die Frage damit nicht beantwortet, sondern lediglich kritisiert wird.
|
|
 |
yukterez

Anmeldungsdatum: 20.09.2014
Beiträge: 96
|
 yukterez Verfasst am: 27. Jul 2016 18:27 Titel: yukterez Verfasst am: 27. Jul 2016 18:27 Titel: |
 |
|
| Zitat: | | Damit sind Gravitationskräfte in der Kosmologie selbst im klassischen Fall ein ziemlich grenzwertiges Konzept. |
Man kann bestens damit rechnen, man muss nur beachten dass es keine bevorzugte Richtung für die Beschleunigung gibt; siehe Alan Guth und Lenny Susskind.
|
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 27. Jul 2016 20:05 Titel: Ich Verfasst am: 27. Jul 2016 20:05 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | Zwischen Testpartikeln in einem unendlichen Newtonschen Universum gibt es zwar klar definierte Gezeitenkräfte, aber die Gravitationskräfte selbst sind unbestimmt. In Abhängigkeit von der Wahl des Bezugssystems können sie jeden beliebigen Wert annehmen. Damit sind Gravitationskräfte in der Kosmologie selbst im klassischen Fall ein ziemlich grenzwertiges Konzept. |
Ja klar. Das sind halt Scheinkräfte, und die verhalten sich nun mal so. Was ist daran grenzwertig? James Watt hat einen Fleihkraftregler erfunden - obwohl es in Inertialsystemen gar keine Fliekräfte gibt.
Solche Konzepte sind nicht grenzwertig, sondern nützlich.
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 27. Jul 2016 21:27 Titel: DrStupid Verfasst am: 27. Jul 2016 21:27 Titel: |
 |
|
| Ich hat Folgendes geschrieben: | | Das sind halt Scheinkräfte, und die verhalten sich nun mal so. |
Nein, in der klassischen Mechanik ist die Gravitationskraft eine echte Wechselwirkungskraft und verhält sich normalerweise ganz und gar nicht so.
| Ich hat Folgendes geschrieben: | | Was ist daran grenzwertig? |
Laut Newtonschem Gravitationsgesetz hängt die Gravitationskraft nur von Masse und Abstand ab und die sind in der klassischen Mechanik beide bezugssystemunabhängig. Wenn die Gravitationskraft bezugssystemabhängig ist, obwohl die Größen, von denen sie abhängt, bezugssystemunabhängig sind, dann sollte das zu denken geben.
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 27. Jul 2016 21:30 Titel: DrStupid Verfasst am: 27. Jul 2016 21:30 Titel: |
 |
|
| yukterez hat Folgendes geschrieben: | | Man kann bestens damit rechnen, man muss nur beachten dass es keine bevorzugte Richtung für die Beschleunigung gibt |
Es gibt nicht nur keine bevorzugte Richtung, sondern auch keinen bevorzugten Betrag für die Beschleunigung in einer klassischen unendlichen homogenen Masseverteilung. Sie ist schlichtweg nicht bestimmbar. Klar definiert sind nur die Gezeitenbeschleunigungen.
|
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 27. Jul 2016 23:05 Titel: Ich Verfasst am: 27. Jul 2016 23:05 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | Ich hat Folgendes geschrieben: | | Das sind halt Scheinkräfte, und die verhalten sich nun mal so. |
Nein, in der klassischen Mechanik ist die Gravitationskraft eine echte Wechselwirkungskraft und verhält sich normalerweise ganz und gar nicht so. |
In der klassischen Mechaniik haben wir dieses vom Himmel gefallene Äquivalenzprinzip, das dafür sorgt, dass diese vermeintlich echte Wechselwirkungskraft sich exakt wie eine Scheinkraft verhält. Und ich verstehe nicht, wieso du deine Antwort mit "Nein" beginnst. Die Gravitationskraft verhält sich wie eine Scheinkraft, weil sie eine ist. Dass man diesen Gedankengang erst nach gut 200 Jahren zu Ende bringen konnte heißt doch nicht, dass er nicht gültig ist.
| Zitat: | | Ich hat Folgendes geschrieben: | | Was ist daran grenzwertig? |
Laut Newtonschem Gravitationsgesetz hängt die Gravitationskraft nur von Masse und Abstand ab und die sind in der klassischen Mechanik beide bezugssystemunabhängig. Wenn die Gravitationskraft bezugssystemabhängig ist, obwohl die Größen, von denen sie abhängt, bezugssystemunabhängig sind, dann sollte das zu denken geben. |
Du bringst das durcheinander. In der prärelativistischen Newtonschen Anschauung sind sowohl die Gravitationskraft als auch die Größen, von denen sie abhängt, bezugssystemunabhängig. Wir haben nur die Eigentümlichkeit, dass die Gravitationskraft nicht eindeutig messbar ist, weil sie nicht von Trägheitskräften zu unterscheiden ist, warum auch immer.
Erst mit Einsteins "glücklichstem Gedanken" 1907 löste sich das auf im Rückblick nachgerade triviale Weise auf: Sie ist nicht von Trägheitskräften zu unterscheiden, weil sie selbst eine ist.
Und erst in diesem Zusammenhang, nachdem ihre Natur als Scheinkraft erkannt war, reden wir von der Bezugssystemabhängiglkeit der Gravitationskraft, und dass ein "homogenes Gravitationsfeld" jederzeit dazuerfunden werden könne und dass die Gravitationskraft lokal jederzeit durch eine einfache Trafo eliminiert werden könne.
Wenn man die Gravitationskraft in diesem - mittlerweile bald 110 Jahre alten - Kontext verwendet, dann gibt es da überhaupt kein Problem. Da ist auch nix grenzwertig.
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 28. Jul 2016 19:09 Titel: DrStupid Verfasst am: 28. Jul 2016 19:09 Titel: |
 |
|
| Ich hat Folgendes geschrieben: | | Die Gravitationskraft verhält sich wie eine Scheinkraft, weil sie eine ist. |
Nein, das tut sie nicht. Scheinkräfte unterscheiden sich von echten Kräften dadurch, dass sie nicht dem dritten Newtonschen Axiom gehorchen. Das Newtonsche Gravitationsgesetz erfüllt alle drei Axiome und beschreibt damit keine Scheinkraft, sondern eine echte Wechselwirkungskraft. Tatsächlich hat Newton seinen Kraftbegriff sogar extra für die Gravitation eingeführt.
| Ich hat Folgendes geschrieben: | | In der prärelativistischen Newtonschen Anschauung sind sowohl die Gravitationskraft als auch die Größen, von denen sie abhängt, bezugssystemunabhängig. |
Es ist zwar schön, dass Du mir wenigstens soweit folgen kannst, aber das nützt wenig, wenn Du den Widerspruch zur Bezugssystemabhängigkeit der Gravitationskräfte in einer unendlichen homogenen Masseverteilung nicht erkennst.
| Ich hat Folgendes geschrieben: | | Wir haben nur die Eigentümlichkeit, dass die Gravitationskraft nicht eindeutig messbar ist |
Wo hast Du das denn her? Natürlich ist die Gravitationskraft eindeutig messbar.
| Ich hat Folgendes geschrieben: | | Und erst in diesem Zusammenhang, nachdem ihre Natur als Scheinkraft erkannt war, reden wir von der Bezugssystemabhängiglkeit der Gravitationskraft |
Offensichtlich hast Du überhaupt nicht verstanden, was ich bisher geschrieben habe: Die auf eine Testmasse innerhalb einer unendlichen homogenen Masseverteilung wirkende Gravitionskraft ist im Rahmen der klassischen Mechanik (!) bezugssystemabhängig, was im Widerspruch zur Tatsache steht, dass sie nur von bezugssystemunabhängigen Größen abhängt.
| Ich hat Folgendes geschrieben: | | Wenn man die Gravitationskraft in diesem - mittlerweile bald 110 Jahre alten - Kontext [ART] verwendet, dann gibt es da überhaupt kein Problem. |
Ich speche ausdrücklich von der klassischen Mechanik.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2016 20:31 Titel: index_razor Verfasst am: 28. Jul 2016 20:31 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | Ich hat Folgendes geschrieben: | | Die Gravitationskraft verhält sich wie eine Scheinkraft, weil sie eine ist. |
Nein, das tut sie nicht. Scheinkräfte unterscheiden sich von echten Kräften dadurch, dass sie nicht dem dritten Newtonschen Axiom gehorchen.
|
Danach könnte man aber auch die Kraft zwischen zwei beliebig bewegten Ladungen als "Scheinkraft" bezeichnen, oder nicht? Oder ist die Verletzung des des 3. Axioms nur ein notwendiges Kriterium für "Scheinkraft"? So oder so, erscheint mir das als recht eigenwillige Abgrenzung. Was spricht gegen die übliche Auffassung von Scheinkräften als Masse mal Beschleunigung eines frei fallenden Teilchens relativ zu einem beschleunigten Bezugssystem?
| Zitat: |
| Ich hat Folgendes geschrieben: | | In der prärelativistischen Newtonschen Anschauung sind sowohl die Gravitationskraft als auch die Größen, von denen sie abhängt, bezugssystemunabhängig. |
Es ist zwar schön, dass Du mir wenigstens soweit folgen kannst, aber das nützt wenig, wenn Du den Widerspruch zur Bezugssystemabhängigkeit der Gravitationskräfte in einer unendlichen homogenen Masseverteilung nicht erkennst.
| Ich hat Folgendes geschrieben: | | Wir haben nur die Eigentümlichkeit, dass die Gravitationskraft nicht eindeutig messbar ist |
Wo hast Du das denn her? Natürlich ist die Gravitationskraft eindeutig messbar.
|
Ich vermute das ist nur eine Umformulierung von deiner -- korrekten --Behauptung der Bezugssystemabhängigkeit der Gravitationskraft. In jedem Fall ist für zwei relativ zueinander beschleunigte Bezugssysteme
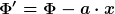
Das bedeutet 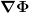 ist (lokal) nicht eindeutig meßbar. Falls ich nun aber die Randbedingung ist (lokal) nicht eindeutig meßbar. Falls ich nun aber die Randbedingung 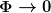 im Unendlichen stellen kann, kann ich entscheiden, welches dieser Bezugssysteme (wenn überhaupt eines) ein globales Inertialsystem ist. Ohne diese Randebdingung kann ich das wegen des Äquivalenzprinzips nicht. In einer homogenen Massenverteilung kann ich aber gerade diese Randbedingung nicht stellen. (Es sei denn das Universum wäre leer.) im Unendlichen stellen kann, kann ich entscheiden, welches dieser Bezugssysteme (wenn überhaupt eines) ein globales Inertialsystem ist. Ohne diese Randebdingung kann ich das wegen des Äquivalenzprinzips nicht. In einer homogenen Massenverteilung kann ich aber gerade diese Randbedingung nicht stellen. (Es sei denn das Universum wäre leer.)
| Zitat: |
| Ich hat Folgendes geschrieben: | | Und erst in diesem Zusammenhang, nachdem ihre Natur als Scheinkraft erkannt war, reden wir von der Bezugssystemabhängiglkeit der Gravitationskraft |
Offensichtlich hast Du überhaupt nicht verstanden, was ich bisher geschrieben habe: Die auf eine Testmasse innerhalb einer unendlichen homogenen Masseverteilung wirkende Gravitionskraft ist im Rahmen der klassischen Mechanik (!) bezugssystemabhängig, was im Widerspruch zur Tatsache steht, dass sie nur von bezugssystemunabhängigen Größen abhängt.
|
Umgekehrt wird ein Schuh draus. Wenn ich die Randbedingung 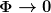 im Unendlichen stellen kann, bin ich in der Lage globale Inertialsysteme anzugeben, bzgl. deren ich ein absolutes Gravitationspotential definieren kann. Jedes andere frei fallende System ist dann eben nur lokal ein Inertialsystem mit zusätzlicher Scheinkraft proportional zur Beschleunigung relativ zum globalen Inertialsystem. Andernfalls habe ich nur lokale Inertialsysteme zwischen denen die Transformation im Unendlichen stellen kann, bin ich in der Lage globale Inertialsysteme anzugeben, bzgl. deren ich ein absolutes Gravitationspotential definieren kann. Jedes andere frei fallende System ist dann eben nur lokal ein Inertialsystem mit zusätzlicher Scheinkraft proportional zur Beschleunigung relativ zum globalen Inertialsystem. Andernfalls habe ich nur lokale Inertialsysteme zwischen denen die Transformation 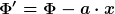 gilt und kein absolutes Gravitationsfeld. gilt und kein absolutes Gravitationsfeld.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Jul 2016 20:44 Titel: index_razor Verfasst am: 28. Jul 2016 20:44 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Ich vermute das ist nur eine Umformulierung von deiner -- korrekten --Behauptung der Bezugssystemabhängigkeit der Gravitationskraft. |
Nein wahrscheinlich doch nicht. Weiter oben hat er die Newtonsche Gravitation als "bezugssystemunabhängig" bezeichnet. Den Punkt muß er also selbst aufklären. Dann haben wir jetzt immerhin drei, statt nur zwei, verschiedenen Meinungen zu diskutieren.
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 28. Jul 2016 21:18 Titel: DrStupid Verfasst am: 28. Jul 2016 21:18 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Danach könnte man aber auch die Kraft zwischen zwei beliebig bewegten Ladungen als "Scheinkraft" bezeichnen, oder nicht? |
Warum?
| index_razor hat Folgendes geschrieben: | | Was spricht gegen die übliche Auffassung von Scheinkräften als Masse mal Beschleunigung eines frei fallenden Teilchens relativ zu einem beschleunigten Bezugssystem? |
Woran erkennt man die Beschleunigung des Bezugssystems?
| index_razor hat Folgendes geschrieben: | | Ich vermute das ist nur eine Umformulierung von deiner -- korrekten --Behauptung der Bezugssystemabhängigkeit der Gravitationskraft. |
Üblicherweise ist die Gravitationskraft in der klassischen Mechanik gerade nicht bezugssytemabhängig.
| index_razor hat Folgendes geschrieben: | Das bedeutet 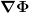 ist (lokal) nicht eindeutig meßbar. ist (lokal) nicht eindeutig meßbar. |
Das Newtonsche Gravitationsgesetz beschreibt keine Kraft in irgend einem Feld, sondern zwischen zwei Körpern und die ist eindeutig messbar.
| index_razor hat Folgendes geschrieben: | Wenn ich die Randbedingung 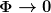 im Unendlichen stellen kann, bin ich in der Lage globale Inertialsysteme anzugeben, bzgl. deren ich ein absolutes Gravitationspotential definieren kann. im Unendlichen stellen kann, bin ich in der Lage globale Inertialsysteme anzugeben, bzgl. deren ich ein absolutes Gravitationspotential definieren kann. |
Ja, wenn. Das geht aber nicht. Tatsächlich ist das Newtonsche Gravitationspotential in einer unendlichen homogenen Masseverteilung überhaupt nicht definiert. Die Newtonsche Gravitationskraft ist dort immerhin endlich, aber eben nicht eindeutig bestimmtbar. Die Gravitationskraft zwischen einem beliebigen Testpartikel und dem Rest der Masseverteilung kann willkürlich gewählt werden. Alle so definierten Bezugssysteme sind vollkommen gleichberechtigt, obwohl sie relativ zueinander beschleunigt sind.
|
|
 |
yukterez

Anmeldungsdatum: 20.09.2014
Beiträge: 96
|
 yukterez Verfasst am: 29. Jul 2016 01:24 Titel: yukterez Verfasst am: 29. Jul 2016 01:24 Titel: |
 |
|
| Zitat: | | Tatsächlich ist das Newtonsche Gravitationspotential in einer unendlichen homogenen Masseverteilung überhaupt nicht definiert. Die Newtonsche Gravitationskraft ist dort immerhin endlich, aber eben nicht eindeutig bestimmtbar. Die Gravitationskraft zwischen einem beliebigen Testpartikel und dem Rest der Masseverteilung kann willkürlich gewählt werden. |
Es ist nur ein kleiner Schritt von Newton zu Gauss und Poisson, siehe auch Timecode t=12m44s:
| Beschreibung: |
|
| Dateigröße: |
49.67 KB |
| Angeschaut: |
8265 mal |

|
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 29. Jul 2016 18:00 Titel: DrStupid Verfasst am: 29. Jul 2016 18:00 Titel: |
 |
|
Warum steht das unter einem Zitat von mir?
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 29. Jul 2016 18:21 Titel: index_razor Verfasst am: 29. Jul 2016 18:21 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Danach könnte man aber auch die Kraft zwischen zwei beliebig bewegten Ladungen als "Scheinkraft" bezeichnen, oder nicht? |
Warum?
|
Weil ein Teil des Impulses zu einer bestimmten Zeit, oder vielleicht für immer, im elektromagnetischen Feld landet. Zumindest muß man präzisieren, was man in diesem Fall unter dem 3. Axiom versteht. Oder sprichst du einfach von Impulserhaltung des Gesamtsystems inklusive aller Felder?
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Was spricht gegen die übliche Auffassung von Scheinkräften als Masse mal Beschleunigung eines frei fallenden Teilchens relativ zu einem beschleunigten Bezugssystem? |
Woran erkennt man die Beschleunigung des Bezugssystems?
|
Mit Hilfe des Trägheits- und Äquivalenzprinzips. Das Trägheitsprinzip sagt dir wann sich ein Beobachter geradlinig gleichförmig bewegt und definiert den Begriff der Parallelverschiebung. Das Äquivalenprinzip sagt, daß "geradlinig gleichförmig" und "schwerelos" dasselbe ist. Ein unbeschleunigtes Bezugssystem ist dann das eines schwerelosen Beobachters, der seine Raumachsen parallelverschiebt. Jedes andere ist "beschleunigt". (Der Begriff ist äquivalent zum lokalen Inertialsystem)
Physikalisch realisiert wird es z.B. durch einen frei fallenden Beobachter im Ursprung, der drehungsfrei gelagerte orthogonale Achsen mitführt, deren Richtung z.B. durch Gyroskope definiert wird.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Ich vermute das ist nur eine Umformulierung von deiner -- korrekten --Behauptung der Bezugssystemabhängigkeit der Gravitationskraft. |
Üblicherweise ist die Gravitationskraft in der klassischen Mechanik gerade nicht bezugssytemabhängig.
|
Weil ich üblicherweise eine Klasse globaler Inertialsysteme definieren kann. (Für eine endliche Menge von Massenpunkten, die sich gegenseitig anziehen, ist dies ja kein Problem.) Lokal gibt es keine Möglichkeit zu entscheiden, welcher von zwei frei fallenden Beobachtern an einem Ort x die korrekte Gravitationskraft mißt.
| Zitat: |
| index_razor hat Folgendes geschrieben: | Das bedeutet 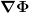 ist (lokal) nicht eindeutig meßbar. ist (lokal) nicht eindeutig meßbar. |
Das Newtonsche Gravitationsgesetz beschreibt keine Kraft in irgend einem Feld, sondern zwischen zwei Körpern und die ist eindeutig messbar.
|
Und was hat dieses Newtonsche Gravitationsgesetz über ein homogenes unendliches Universum zu sagen? Doch überhaupt nichts. Ich dachte wir reden von der allgemeinen Situation, in der ich Poisson-Gleichung löse um mit dem Resultat die Bewegung von Testteilchen zu bestimmen.
| Zitat: |
| index_razor hat Folgendes geschrieben: | Wenn ich die Randbedingung 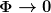 im Unendlichen stellen kann, bin ich in der Lage globale Inertialsysteme anzugeben, bzgl. deren ich ein absolutes Gravitationspotential definieren kann. im Unendlichen stellen kann, bin ich in der Lage globale Inertialsysteme anzugeben, bzgl. deren ich ein absolutes Gravitationspotential definieren kann. |
Ja, wenn. Das geht aber nicht. Tatsächlich ist das Newtonsche Gravitationspotential in einer unendlichen homogenen Masseverteilung überhaupt nicht definiert.
|
Eben, genau das sage ich ja. Das Problem tritt im allgemeinen auf, wenn es frei fallende Beobachter gibt, die relativ zueinander beschleunigen, was im Gravitationsfeld die Regel und nicht die Ausnahme ist. Diese Beobachter können durch lokale Messungen die "korrekte" Gravitationskraft zunächst nicht feststellen. An ihrem eigenen Ort ist jeweils F=0, am Ort des anderen gilt F=-a, wobei a die relative Beschleunigung ist. Sie benötigen zur absoluten Bestimmung ein globales Referenzsystem.
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 29. Jul 2016 20:12 Titel: DrStupid Verfasst am: 29. Jul 2016 20:12 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Weil ein Teil des Impulses zu einer bestimmten Zeit, oder vielleicht für immer, im elektromagnetischen Feld landet. |
Nicht in der klassischen Mechanik. Da haben Felder keine Masse und somit auch keinen Impuls.
| index_razor hat Folgendes geschrieben: | | Das Trägheitsprinzip sagt dir wann sich ein Beobachter geradlinig gleichförmig bewegt |
Ja, wenn in einem Inertialsystem keine Kräfte auf ihn wirken.
| index_razor hat Folgendes geschrieben: | | und definiert den Begriff der Parallelverschiebung. |
Nein, der wird in der Mathematik definiert.
| index_razor hat Folgendes geschrieben: | | Das Äquivalenprinzip sagt, daß "geradlinig gleichförmig" und "schwerelos" dasselbe ist. |
Das Äquivalenzprinzip besagt, dass alle Inertialsysteme gleichberechtigt sind. Dass "geradlinig gleichförmig" und "schwerelos" dasselbe ist, wäre mir neu. Ein Raumschiff im Orbit ist beispielsweise auch schwerelos, obwohl es sich nicht geradlinig-gleichförmig bewegt. Verwechselst Du das mit dem ersten Axiom, nach dem „geradlinig gleichförmig“ gleichbedeutend mit „kräftefrei“ ist?
| index_razor hat Folgendes geschrieben: | | Ein unbeschleunigtes Bezugssystem ist dann das eines schwerelosen Beobachters, der seine Raumachsen parallelverschiebt. |
Auch das passt nicht zum Raumschiff im Orbit. Es ist schwerelos, verschieb seine Achsen entlang des Orbits parallel, aber sein Ruhesystem ist in der klassischen Mechanik kein Inertialsystem.
| index_razor hat Folgendes geschrieben: | | Physikalisch realisiert wird es z.B. durch einen frei fallenden Beobachter im Ursprung, der drehungsfrei gelagerte orthogonale Achsen mitführt, deren Richtung z.B. durch Gyroskope definiert wird. |
Woher weiß man dass der Beobachter frei fallend ist?
Deine Definition von Scheinkräften erscheint mir bis jetzt nicht nur unnötig kompliziert, sondern auch ziemlich schwammig.
| index_razor hat Folgendes geschrieben: | | Und was hat dieses Newtonsche Gravitationsgesetz über ein homogenes unendliches Universum zu sagen? |
Dass es entweder expandiert oder kollabiert und wie das genau passiert.
| index_razor hat Folgendes geschrieben: | | Ich dachte wir reden von der allgemeinen Situation, in der ich Poisson-Gleichung löse um mit dem Resultat die Bewegung von Testteilchen zu bestimmen. |
Das führt zum selben Resultat.
| index_razor hat Folgendes geschrieben: | | Das Problem tritt im allgemeinen auf, wenn es frei fallende Beobachter gibt, die relativ zueinander beschleunigen, was im Gravitationsfeld die Regel und nicht die Ausnahme ist. |
Dass das Gravitationspotential nicht definiert ist, ist durchaus eine Ausnahme in der klassischen Mechanik und relativ zueinander beschleunigte frei fallende Beobachter sind dafür keine hinreichende Bedingung. Mit denen hat man da ständig zu tun, ohne dass es damit irgendwelche Probleme gibt.
| index_razor hat Folgendes geschrieben: | | Sie benötigen zur absoluten Bestimmung ein globales Referenzsystem. |
Weder genügt das, noch ist es die Ursache des Problems. Die Bestimmung der absoluten Beschleunigung in einer unendlichen homogenen Masseverteilung scheitert nicht am Fehlen eines globalen Referenzssystem, sondern daran, dass es zu viele davon gibt und nicht festgestellt werden kann, welches davon absolut unbeschleunigt ist und welches nicht.
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 30. Jul 2016 02:37 Titel: VeryApe Verfasst am: 30. Jul 2016 02:37 Titel: |
 |
|
| ich hat Folgendes geschrieben: | | James Watt hat einen Fleihkraftregler erfunden - obwohl es in Inertialsystemen gar keine Fliekräfte gibt. |
ahja?
Wie würdest du denn die Kraft von der Kugel auf die Pendelstütze taufen,
mit der die Pendelstütze nach oben gedreht wird bzw, in die Länge gezogen wird und das ganze Werk regelt.
bzw kann man es ihn übel nennen wenn er diese Kraft Fliehkraft tauft, da sie aus dem Fliehen der Kugel resultiert und dadurch sein ganzes Werk geregelt wird.
oder die Kraft die beim Schleudern der Wäsche von der Wäsche auf die Trommel drückt.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 30. Jul 2016 09:36 Titel: index_razor Verfasst am: 30. Jul 2016 09:36 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Weil ein Teil des Impulses zu einer bestimmten Zeit, oder vielleicht für immer, im elektromagnetischen Feld landet. |
Nicht in der klassischen Mechanik. Da haben Felder keine Masse und somit auch keinen Impuls.
|
Das elektromagnetische Feld hat weder klassisch, noch nicht-klassisch eine Masse, aber trotzdem einen Impuls. Es wundert mich schon etwas, daß du meinst Masse wäre eine Voraussetzung für Impuls.
Davon abgesehen verstehe ich immer noch nicht wie das 3. Axiom auf die elektromagnetische Wechselwirkung, oder allgemein auf Wechselwirkungen mit endlicher Ausbreitungsgeschwindigkeit, angewendet wird. Fordert man, daß zu jedem Zeitpunkt in einem Zweiteilchensystem 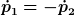 gelten soll? Man muß doch irgendwie die Retardierung berücksichtigen, oder nicht? gelten soll? Man muß doch irgendwie die Retardierung berücksichtigen, oder nicht?
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Das Trägheitsprinzip sagt dir wann sich ein Beobachter geradlinig gleichförmig bewegt |
Ja, wenn in einem Inertialsystem keine Kräfte auf ihn wirken.
|
Wenn keine Kräfte auf ihn wirken. Punkt. Ob eine physikalische Wechselwirkung mit einem anderen Objekt stattfindet, die ihn von seiner Trägheitsbahn ablenkt, ist eine vom Bezugssystem unabhängige Frage.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | und definiert den Begriff der Parallelverschiebung. |
Nein, der wird in der Mathematik definiert.
|
Und in der Physik verwendet. Der physikalische Hintergrund dieser Definition ist in der Mechanik das Trägheitsprinzip.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Das Äquivalenprinzip sagt, daß "geradlinig gleichförmig" und "schwerelos" dasselbe ist. |
Das Äquivalenzprinzip besagt, dass alle Inertialsysteme gleichberechtigt sind.
|
Nein, das ist das Relativitätsprinzip. Das Äquivalenzprinzip besagt, daß Testteilchen im Gravitationsfeld universellen Bahnen folgen. Im mitfallenden lokalen Inertialsystem sind ihre Bewegungsgleichungen durch 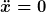 gegeben, d.h. sie bewegen sich geradlinig gleichförmig. gegeben, d.h. sie bewegen sich geradlinig gleichförmig.
Koordinatenunabhängig drückt man dies mit Hilfe der Parallelverschiebung aus, d.h. das Testteilchen verschiebt seinen eigenen Geschwindigkeitsvektor parallel durch die Newtonsche Raumzeit.
| Zitat: |
Dass "geradlinig gleichförmig" und "schwerelos" dasselbe ist, wäre mir neu.
Ein Raumschiff im Orbit ist beispielsweise auch schwerelos, obwohl es sich nicht geradlinig-gleichförmig bewegt. Verwechselst Du das mit dem ersten Axiom, nach dem „geradlinig gleichförmig“ gleichbedeutend mit „kräftefrei“ ist?
|
Willkommen in der gekrümmten Raumzeit Newtons. Verbindet man die Gleichheit von Schwere und Trägheit mit dem 1. Axiom, so ergibt sich ganz zwanglos, daß die lokale Bedingung für Geradlinig-Gleichförmigeit, 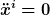 , zu global "gekrümmten" Bahnkurven führt. , zu global "gekrümmten" Bahnkurven führt.
Das ist im Kontext der Newtonschen Mechanik noch immer ungewohnt, aber nicht neu. (Es geht meines Wissens auf E. Cartan zurück.) Die Alternative ist die Auszeichnung einer Klasse von Inertialsystemen, gegen die man "Flachheit" und ein absolutes Gravitationspotential definieren kann. Das Äquivalenzprinzip ist dann eher eine Zufälligkeit, die verhindert, daß man dieses absolute Potential durch lokale Messungen feststellen kann. Dies hat den Nachteil, daß sich außer in speziellen Situation (die für normale Anwendungen der Theorie typisch sein mögen) keine ausgezeichnete Klasse solcher Inertialsysteme anbietet, und der Begriff des "lokalen Gravitationspotentials" eine theoretische Fiktion wird.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Ein unbeschleunigtes Bezugssystem ist dann das eines schwerelosen Beobachters, der seine Raumachsen parallelverschiebt. |
Auch das passt nicht zum Raumschiff im Orbit. Es ist schwerelos, verschieb seine Achsen entlang des Orbits parallel, aber sein Ruhesystem ist in der klassischen Mechanik kein Inertialsystem.
|
Doch ist es. Die Insassen haben alle abschirmbaren Kräfte von einem Testteilchen abgeschirmt. Dieses folgt dann nur seiner Trägheit und seine Trägheit ist gleich seiner Schwere. Die Konsequenz ist die Bewegungsgleichung
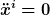 . .
Wenn kräftefreie Teilchen innerhalb eines Bezugssystems diesem Bewegungsgesetz folgen, bezeichnet man das System als lokales Inertialsystem.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Physikalisch realisiert wird es z.B. durch einen frei fallenden Beobachter im Ursprung, der drehungsfrei gelagerte orthogonale Achsen mitführt, deren Richtung z.B. durch Gyroskope definiert wird. |
Woher weiß man dass der Beobachter frei fallend ist?
|
Weil er sein Gewicht mißt und mitteilt, daß es den Wert null hat.
| Zitat: |
Deine Definition von Scheinkräften erscheint mir bis jetzt nicht nur unnötig kompliziert, sondern auch ziemlich schwammig.
|
Sie ist nicht schwammig. Sie basiert auf dem recht präzisen Fundament des affinen Zusammenhangs. Weiter oben war dir das noch zu mathematisch.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Und was hat dieses Newtonsche Gravitationsgesetz über ein homogenes unendliches Universum zu sagen? |
Dass es entweder expandiert oder kollabiert und wie das genau passiert.
|
Ein Zweiteilchen-Kraftgesetz sagt dir, daß ein homogenes Universum expandiert oder kollabiert? Wie soll das gehen?
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Ich dachte wir reden von der allgemeinen Situation, in der ich Poisson-Gleichung löse um mit dem Resultat die Bewegung von Testteilchen zu bestimmen. |
Das führt zum selben Resultat.
|
Zu welchem Resultat genau führt es denn?
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Das Problem tritt im allgemeinen auf, wenn es frei fallende Beobachter gibt, die relativ zueinander beschleunigen, was im Gravitationsfeld die Regel und nicht die Ausnahme ist. |
Dass das Gravitationspotential nicht definiert ist, ist durchaus eine Ausnahme in der klassischen Mechanik und relativ zueinander beschleunigte frei fallende Beobachter sind dafür keine hinreichende Bedingung. Mit denen hat man da ständig zu tun, ohne dass es damit irgendwelche Probleme gibt.
|
Ich dachte du siehst es als Problem an, daß das Potential in bestimmten Situationen nicht beobachterunabhängig definiert ist. Das ist eine Konsequenz des Äquivalenzprinzips und damit die Regel.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Sie benötigen zur absoluten Bestimmung ein globales Referenzsystem. |
Weder genügt das, noch ist es die Ursache des Problems. Die Bestimmung der absoluten Beschleunigung in einer unendlichen homogenen Masseverteilung scheitert nicht am Fehlen eines globalen Referenzssystem, sondern daran, dass es zu viele davon gibt und nicht festgestellt werden kann, welches davon absolut unbeschleunigt ist und welches nicht. |
Vielleicht ist meine Terminologie "globales Inertialsystem" nicht glücklich gewählt. Das, wovon es zu viele gibt, sind lokale Inertialsysteme. Davon mußt du eine Klasse auszeichnen, um von absoluter Beschleunigung sprechen zu können. (Das geht z.B. in Inseluniversen, mit beschränkter Materieverteilung.) Diese Klasse nannte ich "globale Inertialsysteme". (Sie sind aber nicht globaler, als die lokalen, in dem Sinne, daß sie mehr von der Raumzeit aufspannen.) Besser wäre vielleicht "absolutes Inertialsystem".
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 30. Jul 2016 14:27 Titel: DrStupid Verfasst am: 30. Jul 2016 14:27 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Das elektromagnetische Feld hat weder klassisch, noch nicht-klassisch eine Masse, aber trotzdem einen Impuls. Es wundert mich schon etwas, daß du meinst Masse wäre eine Voraussetzung für Impuls. |
Der Impuls ist in der klassischen Mechanik als Produkt von Masse und Geschwindigkeit definiert.
| index_razor hat Folgendes geschrieben: | | Davon abgesehen verstehe ich immer noch nicht wie das 3. Axiom auf die elektromagnetische Wechselwirkung, oder allgemein auf Wechselwirkungen mit endlicher Ausbreitungsgeschwindigkeit, angewendet wird. |
In der klassischen Mechanik gibt es keine Fernwirkungen mit endlicher Ausbreitungsgeschwindigkeit.
Wenn Du verstehen willst, was ich schreibe, dann musstt Du aufhören klassische und nicht-klassische Konzepte zu vermischen.
| index_razor hat Folgendes geschrieben: | | Wenn keine Kräfte auf ihn wirken. Punkt. |
Das erste Axiom darf nicht unabhängig von den anderen beiden verwendet werden. Alle drei Axiome haben einen gemeinsamen Gültigkeitsbereich – nämlich Inertialsysteme. Wenn eines der Axiome nicht erfüllt ist, hat man es mit einem Nicht-Inertialsystem zu tun und da gelten dann auch die anderen beiden Axiome nicht mehr.
Das bedeutet unter anderem, dass ein Körper sich in einem Nicht-Inertialsystem auch dann geradlinig gleichförmig bewegen kann, wenn Kräfte auf ihn wirken – nämlich genau dann wenn die auf ihn wirkenden Kräfte und Scheinkräfte sich gegenseitig aufheben.
Newton hat das dritte Axiom später zwar so geändert, dass es in Nicht-Iniertialsystemen nicht mehr verletzt wir, aber das hat sich nicht durchgesetzt. Ich spreche hier über die ursprüngliche Version und da ist die Abwesenheit von Kräften nur in Inertialsystemen hinreichend für geradlinig gleichförmige Bewegung.
| index_razor hat Folgendes geschrieben: | | Willkommen in der gekrümmten Raumzeit Newtons. |
Sowas gibt es nicht. Newton verwendet einen Euklidischen Raum und eine davon unabhängige Zeit.
| index_razor hat Folgendes geschrieben: | | Wenn kräftefreie Teilchen innerhalb eines Bezugssystems diesem Bewegungsgesetz folgen, bezeichnet man das System als lokales Inertialsystem. |
Mit der Einschränkung auf lokale Inertialsysteme ist Deine Aussage zwar nicht mehr falsch, aber jetzt brauchst Du eine unabhängige Definition von „kräftefrei“.
| index_razor hat Folgendes geschrieben: | | Weil er sein Gewicht mißt und mitteilt, daß es den Wert null hat. |
Und wie misst er sein Gewicht? Bevor Du antwortest, solltest Du Dir das hier ansehen:
https://youtu.be/A1vyB-O5i6E
| index_razor hat Folgendes geschrieben: | | Ein Zweiteilchen-Kraftgesetz sagt dir, daß ein homogenes Universum expandiert oder kollabiert? Wie soll das gehen? |
Durch Integration.
| index_razor hat Folgendes geschrieben: | | Zu welchem Resultat genau führt es denn? |
Es führt zur Differentialgleichung

für den Skalenfaktor und durch anschließende Integration über die Zeit zur Gleichung

welche in Abhängigkeit von der Integrationskonstante K drei Szenarien beschreibt:
geschlossenes Universum: K<0
flaches Universum: K=0
offenes Universum: K>0
Darin stimmt das Resultat überraschend gut mit einfachen relativistischen kosmologischen Modellen überein. Für K=0 ergibt die weitere Integration mit

sogar exakt dasselbe Ergebnis wie die ART (Einstein-de Sitter-Modell).
| index_razor hat Folgendes geschrieben: | | Ich dachte du siehst es als Problem an, daß das Potential in bestimmten Situationen nicht beobachterunabhängig definiert ist. |
Davon abgesehen, dass das Potential nichts mit dem Problem zu tun hat über das wir hier reden, ist es in der klassischen Mechanik normalerweise immer beobachterunabhängig definiert. Daran ändert auch das Äquivalenzprinzip nichts.
| index_razor hat Folgendes geschrieben: | | Das, wovon es zu viele gibt, sind lokale Inertialsysteme. |
In einer unendlichen homogenen Masseverteilung ist jedes nicht-rotierende Bezugssystem, in dem der Schwerpunkt einer kugelförmigen Teilmasse ruht oder geradlinig gleichförmig bewegt ist, ein globales Inertialsystem. Davon gibt es unendlich viele und die Zahl derjenigen Inertialsysteme, die relativ zueinander beschleunigt sind, ist ebenfalls unendlich.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 31. Jul 2016 10:49 Titel: index_razor Verfasst am: 31. Jul 2016 10:49 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: |
Wenn Du verstehen willst, was ich schreibe, dann musstt Du aufhören klassische und nicht-klassische Konzepte zu vermischen.
|
Im Augenblick versuche ich eigentlich nur zu verstehen, ob du die EM-Kraft als Scheinkraft siehst oder nicht und warum. Also wie verhält es sich denn nun?
1) Ja, Scheinkraft, weil sie das 3. Axiom verletzt.
2) Nein, weil sie das 3. Axiom erfüllt und zwar in der Formulierung...
3) Unentscheidbar, weil Verletzung des 3. Axioms lediglich notwendig für das Vorliegen einer Scheinkraft ist und deshalb keinen positiven Beweis erlaubt, daß etwas eine Scheinkraft ist.
4) Unentscheidbar, weil man ein klassisches Axiom nicht auf nicht-klassische Konzepte anwenden kann.
5) ...
Darüberhinaus ist es m.E. nicht weiter von Interesse, ob du das klassische EM-Feld als "nicht-klassisches Konzept" einordnest oder welche Definition von Impuls du meinst gestatten zu können.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Wenn keine Kräfte auf ihn wirken. Punkt. |
Das erste Axiom darf nicht unabhängig von den anderen beiden verwendet werden. Alle drei Axiome haben einen gemeinsamen Gültigkeitsbereich – nämlich Inertialsysteme. Wenn eines der Axiome nicht erfüllt ist, hat man es mit einem Nicht-Inertialsystem zu tun und da gelten dann auch die anderen beiden Axiome nicht mehr.
|
Interessant daran ist, daß praktisch dieselbe Behauptung mal über die SRT verbreitet war. Diese verlor ihren Gültigkeitsbereich angeblich auch außerhalb von Inertialsystemen. Inzwischen wird das aber immer seltener vorgebracht, wobei m.E. die bezugssystemunabhängige Formulierung der Theorie sehr hilfreich war. Vielleicht gibst du dem Ganzen -- auch wenn du weiter unten behauptest, es gäbe so eine Formulierung gar nicht -- doch mal eine Chance. Auch die Gesetze der Newtonschen Mechanik gelten völlig unabhängig vom Bezugsystem.
Außerdem scheint in deiner jetzigen Erklärung die Verletzung des 3. Axioms nicht auschlaggebender zu sein, als die Verletzung der anderen Axiome. Entweder gelten sie alle oder keins. Warum hebst du also das 3. Axiom als Kriterium für Scheinkräfte hervor? Es sieht so aus als ob du mir jetzt zustimmst, daß Scheinkräfte nur in Nicht-Inertialsystemen auftreten und die Verletzung der Axiome betrachtest du lediglich als Kriterium für "Nicht-Inertialität". Anders ergibt das keinen Sinn mehr für mich.
| Zitat: |
Das bedeutet unter anderem, dass ein Körper sich in einem Nicht-Inertialsystem auch dann geradlinig gleichförmig bewegen kann, wenn Kräfte auf ihn wirken – nämlich genau dann wenn die auf ihn wirkenden Kräfte und Scheinkräfte sich gegenseitig aufheben.
|
Nein, das bedeutet, daß in einem Nicht-Inertialsystem die Gleichung  nicht mehr äquivalent ist zur Geradlinig-Gleichförmigkeit. An ihre Stelle tritt nicht mehr äquivalent ist zur Geradlinig-Gleichförmigkeit. An ihre Stelle tritt
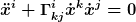 . .
Oder anders ausgedrückt sind lokale Inertialsysteme durch das verschwinden aller 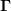 im Ursprung definiert. im Ursprung definiert.
Außerdem hast du hier jetzt ein logisches Problem. Daß bestimmte Axiome nicht mehr gelten, bedeutet erst mal gar nichts, außer daß ich neue Axiome brauche. Woraus willst du nun deinen Schluß gezogen haben, daß sich ein Körper in einem Nicht-Inertialsystem unter Einwirkung einer Kraft geradlinig-gleichförmig bewegen kann? Aus dem Verschwinden irgendeiner Gesamtkraft folgt das nur mit Hilfe einer allgemeinen Aussage über den Zusammenhang von Beschleunigung und Kraft, den normalerweise das 2. Axiom angibt.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Willkommen in der gekrümmten Raumzeit Newtons. |
Sowas gibt es nicht. Newton verwendet einen Euklidischen Raum und eine davon unabhängige Zeit.
|
Und du hältst beides für unvereinbar mit einer gekrümmten Raumzeit? Ich gehe mal davon aus, daß du nicht lediglich die Meinung ausdrückst, daß es soetwas in der physikalischen Realität nicht gäbe. Denn das wäre ein Eiwand gegen die gesamte Newtonsche Mechanik.
Also entweder du behauptest, Cartan hätte sich mit Strukturen beschäftigt, die nichtmal im theoretischen Sinne existieren und es leider nicht gemerkt. Oder ich hätte mir die ganze Sache nur eingebildet.
Die gekrümmte Newtonsche Raumzeit existiert in genau demselben Sinne, wie die gekrümmte Einsteinsche Raumzeit. Sie hat lediglich andere Eigenschaften, zu denen, nebenbei bemerkt, auch eine absolute Zeit und ein euklidischer Raum gehört. Von letzterem besitzt sie sogar unendlich viele, nämlich für jeden absoluten Zeitpunkt einen. Und sie ist nichtsdestoweniger gekrümmt.
Oder vielleicht behauptest du auch, diese Struktur existiere zwar, man dürfe sie aber nicht "Newtonsche Raumzeit" nennen, weil Newton sie sich nicht ausgedacht hat. Dann wäre der Einwand vollkommen uninteressant, denn wie du sie nennst ist ja völlig egal, von mir aus "Cartansche Raumzeit". Diese wäre aber sowohl in mathematischer als auch physikalisch-empirischer Hinsicht völlig äquivalent zur Theorie Newtons. Die Verwandschaft ist analog zu der zwischen Minkowskis Version der SRT und Einsteins ursprünglicher. Heutzutage verwenden wir fast ausschließlich die Formulierung von Minkowski und nennen es trotzdem nicht "Minkowskische Relativitätstheorie".
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Wenn kräftefreie Teilchen innerhalb eines Bezugssystems diesem Bewegungsgesetz folgen, bezeichnet man das System als lokales Inertialsystem. |
Mit der Einschränkung auf lokale Inertialsysteme ist Deine Aussage zwar nicht mehr falsch, aber jetzt brauchst Du eine unabhängige Definition von „kräftefrei“.
|
Wieso "nicht mehr"? Welche Aussage war denn vorher falsch? Außerdem ist "lokales Inertialsystem" keine Einschränkung, sondern eine Verallgemeinerung. Schließlich ist jedes Inertialsystem auch ein lokales Inertialsystem und letzteres somit eine größere Klasse. Deine Bemerkung ergibt also m.E. keinen Sinn. (Streng genommen wird meine Aussage durch die Verallgemeinerung sogar falsch, denn ich hätte sagen sollen, daß kräftefreie Teilchen die Gl. 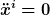 nur in der Nähe des Ursprungs eines lokalen Inertialsystems erfüllen müssen. Ansonsten ist die Bedingung zu streng.) nur in der Nähe des Ursprungs eines lokalen Inertialsystems erfüllen müssen. Ansonsten ist die Bedingung zu streng.)
Im übrigen lautet meine Definition von "kräftefrei", daß alle lokal am Ort des Teilchens meßbare Wechselwirkungen mit anderen Teilchen sich aufheben. Das ist natürlich eher ein physikalisches Kriterium als eine Definition und läßt sich auch nur mit Hilfe konkreter Gesetzmäßigkeiten erörtern, die solche potentiellen Wechselwirkungen beschreiben. Aber mit Definitionen allein kommt man nicht weit. Irgendwo muß man ja anfangen. Aus rein theoretischer Sicht betrachte ich "kräftfrei" und "geradlinig-gleichförmig" auf Grund des Trägheitsprinzips (bezugssystemunabhängig aufgefaßt) als stets gleichzeitig erfüllt und damit "definiert" von mir aus der eine Begriff den anderen.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Weil er sein Gewicht mißt und mitteilt, daß es den Wert null hat. |
Und wie misst er sein Gewicht? Bevor Du antwortest, solltest Du Dir das hier ansehen:
https://youtu.be/A1vyB-O5i6E
|
Er schirmt alle lokal von ihm meßbaren Wechselwirkungen mit anderen Körpern von sich selbst ab. Dann hängt er sich an eine Feder, die relativ zu ihm ruht. (M.a.W. die Federkraft ist die einzige, die noch auf ihn wirkt.) Die Differenz der Federauslenkung zwischen alter und neuer Ruhelage ist proportional zu seinem Gewicht. Aber warum fragst du eigentlich? Bezweifelst du, daß es ihm irgendwie prinzipiell möglich ist, sein eigenes Gewicht zu messen? Oder willst du nur sehen, an welchem Punkt ich nicht mehr weiter weiß?
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Ein Zweiteilchen-Kraftgesetz sagt dir, daß ein homogenes Universum expandiert oder kollabiert? Wie soll das gehen? |
Durch Integration.
|
Das vertehe ich nicht. Berechnest du
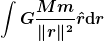
oder was? Oder redest du von der Lösung der Poisson-Gleichung oder wovon?
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Zu welchem Resultat genau führt es denn? |
Es führt zur Differentialgleichung

für den Skalenfaktor
|
Welcher Skalenfaktor? Ich dachte du redest vom Newtonschen Gravitationsgesetz.
)
(Den Rest der Rechnung kann ich zwar formal nachvollziehen, aber beurteilen kann ich das nicht, da mir deine Voraussetzungen vollkommen unklar sind.)
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Ich dachte du siehst es als Problem an, daß das Potential in bestimmten Situationen nicht beobachterunabhängig definiert ist. |
Davon abgesehen, dass das Potential nichts mit dem Problem zu tun hat über das wir hier reden, ist es in der klassischen Mechanik normalerweise immer beobachterunabhängig definiert. Daran ändert auch das Äquivalenzprinzip nichts.
|
Das Äquivalenzprinzip besagt (oder es folgt aus ihm--je nach Formulierung), daß ein frei fallender Beobachter lokal keine Gravitationskraft mißt. Ein weiter entfernter frei fallender Beobachter stellt auf Grund von dessen Bewegung (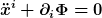 ) am Ort des ersten aber die Gravitationskraft ) am Ort des ersten aber die Gravitationskraft 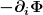 fest. fest.
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 31. Jul 2016 13:28 Titel: VeryApe Verfasst am: 31. Jul 2016 13:28 Titel: |
 |
|
Darf ich hier auch etwas fragen.
ich möchte festhalten ich habe eine 3d Raumbegriff und die Zeit extra, das Raumbild der klassischen Mechanik.
Ich dachte das Äquivalenzprinzip besagt das schwere und träge Masse gleich sind, das in weiterer Folge mit den Newton Gravitationsgesetz, alle Objekte am selben Radius die selbe Graviationsbeschleunigung vom Betrag her erfahren, aber nicht zwangsweise dieselbe Richtung.
Aber alle Objekte die sich am selben Radius in einen eingeengte Raumgebiet also lokal auch die selbe Richtung der Beschleunigung erfahren, und damit der Betrachtung einen beschleunigten Bezugsystem gleichkommen und die Gravitationskraft einer Trägheitskraft die man wegtranformieren kann, wenn man sich in das Bezugssystemm mit -g setzt.
Nimmt man jetzt einen Kasten mit kleiner Ausdehnung positioniert Objekte, lässt alles samt den Kasten darin frei fallen so kann man nicht feststellen, ob man jetzt in einen Inertialsystem ist oder in einen freifallenden Bezugsystem.
Es ist also lokal beschränkt gleichwertig.
Dabei ist es aber doch wichtig, daß man nur das betrachtet was im Kasten ist, Wenn man aus den Kasten schaut und in die Umgebung global kann man sehr wohl feststellen das man sich laut klassicher Mechanik nicht in einem Inertialsystem befindet.
Man kann nur so tun als wäre man im Inertialsystem wenn man nur alles im Kasten betrachtet, sonst bekomme ich doch Probleme, wenn ich zum Beispiel erklären muß wieso nun die Erde mit g auf mich zubeschleunigt und alle anderen Objekte in ihren Orbit.
Die Gravitationskraft ist hier eine echte Wechselwirkungskraft
| indexrazor hat Folgendes geschrieben: | | Auch die Gesetze der Newtonschen Mechanik gelten völlig unabhängig vom Bezugsystem. |
das kann ich überhaupt nicht nachvollziehen.
Die Newtonschen Axiome gelten im Inertialsystem.
wechselt man in ein Nichtinertialsystem so hätte Newton gleich sein erstes Axiom umschreiben müssen in :
ein körper bewegt sich geradlinig oder auf krummen Bahnen keinesfalls gleichförmig wenn auf ihn keine äußeren Kräfte wirken
Er beschleunigt einfach kraftlos.
damit wäre auch gleich sein 2.Axiom hinfällig gewesen im nicht Inertialsystem
Die Änderung der Bewegung ist der Einwirkung der bewegenden Kraft proportional und geschieht nach der Richtung derjenigen geraden Linie, nach welcher jene Kraft wirkt.
Es gibt eine Bewegungsänderung obwohl es gar keine Kraft gibt.
übernimmt er aber jetzt die ersten zwei Axiome und wendet sie an,
So gibt es in Nichtinertialsystem eine Scheinkraft, aber wiederum das dritte Axiom wird verletzt, da es auf diese Scheinkraft kein reactio gibt.
Für mich erscheint das als die einfachste Lösung.
Und ein Nichtinertialsystem erkennt man dann an der Verletzung des 3 axioms
Ich kenne aber keine Lösung indem diese Axiome in allen Bezugssystem einwandfrei funktionieren.
**********************
dann hätte ich an index razor eine Frage. Wie willsd du eine Scheinkraft mit Masse mal Beschleunigung erkennen?
Das ist immerhin das 2 Axiom für m=const, demnach wären alle newtonschen Kräfte scheinkräfte, das kann ich überhaupt nicht nachvollziehen
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 31. Jul 2016 15:12 Titel: index_razor Verfasst am: 31. Jul 2016 15:12 Titel: |
 |
|
| VeryApe hat Folgendes geschrieben: |
Nimmt man jetzt einen Kasten mit kleiner Ausdehnung positioniert Objekte, lässt alles samt den Kasten darin frei fallen so kann man nicht feststellen, ob man jetzt in einen Inertialsystem ist oder in einen freifallenden Bezugsystem.
Es ist also lokal beschränkt gleichwertig.
Dabei ist es aber doch wichtig, daß man nur das betrachtet was im Kasten ist, Wenn man aus den Kasten schaut und in die Umgebung global kann man sehr wohl feststellen das man sich laut klassicher Mechanik nicht in einem Inertialsystem befindet.
|
Das kann man im allgemeinen nicht. Dazu muß es eine ausgezeichnete Klasse von Beobachtern geben, relativ zu denen man seine Beschleunigung feststellt. Aber wie identifiziert man so eine Klasse von Beobachtern im Gravitationsfeld? Oder anders formuliert: Woran erkennst du ein Inertialsystem? Daran, daß die Newtonschen Axiome erfüllt sind? Das ist zirkulär. Nicht falsch verstehen, ich denke nicht, daß man diese Zirkularität auf diesem fundamentalen Niveau vermeiden kann ohne sich tot zu definieren. Die Frage ist nur wo man ansetzt: Bei einer Klasse absoluter Inertialsysteme deren Gegebensein man nicht weiter hinterfragt oder beim Äquivalenzprinzip. Die erste Variante führt auf einen Kraftbegriff, der zu u.U. objektiv gar nicht bestimmbaren Kräften führt, die man willkürlich von anderen Scheinkräften abgrenzt. Die zweite Variante führt auf eine gekrümmte Newtonsche Raumzeit.
| Zitat: |
| indexrazor hat Folgendes geschrieben: | | Auch die Gesetze der Newtonschen Mechanik gelten völlig unabhängig vom Bezugsystem. |
das kann ich überhaupt nicht nachvollziehen.
Die Newtonschen Axiome gelten im Inertialsystem.
wechselt man in ein Nichtinertialsystem so hätte Newton gleich sein erstes Axiom umschreiben müssen in :
ein körper bewegt sich geradlinig oder auf krummen Bahnen keinesfalls gleichförmig wenn auf ihn keine äußeren Kräfte wirken
Er beschleunigt einfach kraftlos.
|
Der Trick ist, daß man den Begriff Kraft nicht so allgemein (um nicht zu sagen inhaltsleer) versteht, daß er von Anfang an "Scheinkräfte" mit umfaßt. Eine Kraft ist etwas objektiv, beobachterunabhängig gegebenes, was auf die Wechselwirkung mit anderen Körpern zurückzuführen ist. In diesem Sinne ist geradlinig-gleichförmig und kräftefrei dasselbe (Trägheitsprinzip). In Nicht-Inertialsystemen werden Geraden lediglich nicht mehr durch die Gl. 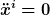 beschrieben. Diese Situation ist nicht ungewöhnlich. Man kennt sie auch von krummlinigen Koordinatensystemen in der euklidischen Geometrie. beschrieben. Diese Situation ist nicht ungewöhnlich. Man kennt sie auch von krummlinigen Koordinatensystemen in der euklidischen Geometrie.
| Zitat: |
damit wäre auch gleich sein 2.Axiom hinfällig gewesen im nicht Inertialsystem
Die Änderung der Bewegung ist der Einwirkung der bewegenden Kraft proportional und geschieht nach der Richtung derjenigen geraden Linie, nach welcher jene Kraft wirkt.
Es gibt eine Bewegungsänderung obwohl es gar keine Kraft gibt.
|
Nein, aus demselben Grund, aus dem ich das Wirken einer Kraft ausschließe, folgere ich, daß die Bewegung geradlinig-gleichförmig verläuft. Wenn keine von allen Beobachtern feststellbare Kraft am Ort des Teilchens wirkt, ist es kräftefrei.
| Zitat: |
übernimmt er aber jetzt die ersten zwei Axiome und wendet sie an,
So gibt es in Nichtinertialsystem eine Scheinkraft, aber wiederum das dritte Axiom wird verletzt, da es auf diese Scheinkraft kein reactio gibt.
Für mich erscheint das als die einfachste Lösung.
|
Die nicht objektiv von allen Beobachtern feststellbare Wechselwirkung mit anderen Körpern ist die Lösung. Welche Axiome diese Wechselwirkungen erfüllen ist ansonsten erstmal zweitrangig.
| Zitat: |
Und ein Nichtinertialsystem erkennt man dann an der Verletzung des 3 axioms
Ich kenne aber keine Lösung indem diese Axiome in allen Bezugssystem einwandfrei funktionieren.
|
Wie ist denn deine Meinung zu retardierten Kräften im Zusammenhang mit dem 3. Axiom?
| Zitat: |
dann hätte ich an index razor eine Frage. Wie willsd du eine Scheinkraft mit Masse mal Beschleunigung erkennen?
Das ist immerhin das 2 Axiom für m=const, demnach wären alle newtonschen Kräfte scheinkräfte, das kann ich überhaupt nicht nachvollziehen |
Ich erkenne das so: Zuerst schließe ich aus, daß am Ort des Teilchens eine meßbare Wechselwirkung mit anderen Teilchen besteht, d.h. es gibt dort kein elektromagnetisches Feld oder das Teilchen ist neutral, etc. (An dieser Stelle willst du wahrscheinlich fragen, warum ich hier "die Gravitationskraft" nicht auch explizit ausschließe. Dazu komme ich gleich.) Wenn dann von meinem Ruhesystem aus betrachtet das Teilchen der Bewegungungsgleichung 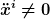 folgt, dann steht es unter dem Einfluß einer "Scheinkraft" oder m.a.W. ich befinde mich nicht im freien Fall oder m.a.W. ich befinde mich nicht in einem Inertialsystem oder ...(dasselbe mit noch anderen Worten formuliert). folgt, dann steht es unter dem Einfluß einer "Scheinkraft" oder m.a.W. ich befinde mich nicht im freien Fall oder m.a.W. ich befinde mich nicht in einem Inertialsystem oder ...(dasselbe mit noch anderen Worten formuliert).
Was ist nun mit der Gravitationskraft? Zunächst gilt für alle anderen Kräfte, daß die Frage, ob sie am Ort des Teilchens wirksam sind oder nicht, von allen Beobachtern, also objektiv, gleich beantwortet wird. Entweder ist dort ein EM-Feld oder nicht. Für die Gravitation andererseits gilt das Äquivalenzprinzip. Ein nahe am Teilchen frei vorbei fallender Beobachter mißt sie nicht. Die Frage ob die Gravitation am Ort des Teilchens wirkt, ist also beobachterabhängig. Aus diesem Grunde ist es sinnvoller die Bewegung von Testteilchen "im Gravitationsfeld" in die Definition von "geradlinig-gleichförmig" aufzunehmen womit die Gravitation selbst zur Scheinkraft wird. Das ist im Prinzip Einsteins "glücklichster Gedanke". In der Newtonschen Physik ist er aber genauso sinnvoll.
|
|
 |
|
|

















